鲁教版(五四制)六年级下数学 第七章 相交线与平行线 1 两条直线的位置关系 课件(共25张PPT)
文档属性
| 名称 | 鲁教版(五四制)六年级下数学 第七章 相交线与平行线 1 两条直线的位置关系 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 10:45:04 | ||
图片预览



文档简介
(共25张PPT)
1 两条直线的位置关系
a
·
·
A
B
1.从生活实例中抽象出相交线、平行线,概括出相交线、平行线的概念;
2.通过具体实例观察对顶角、余角、补角等的特征,认识对顶角、余角、补角概念;
3.探索并说出对顶角相等,同角(等角)的余角相等,同角(等角)的补角相等的性质,并能用这些性质解决一些简单问题。
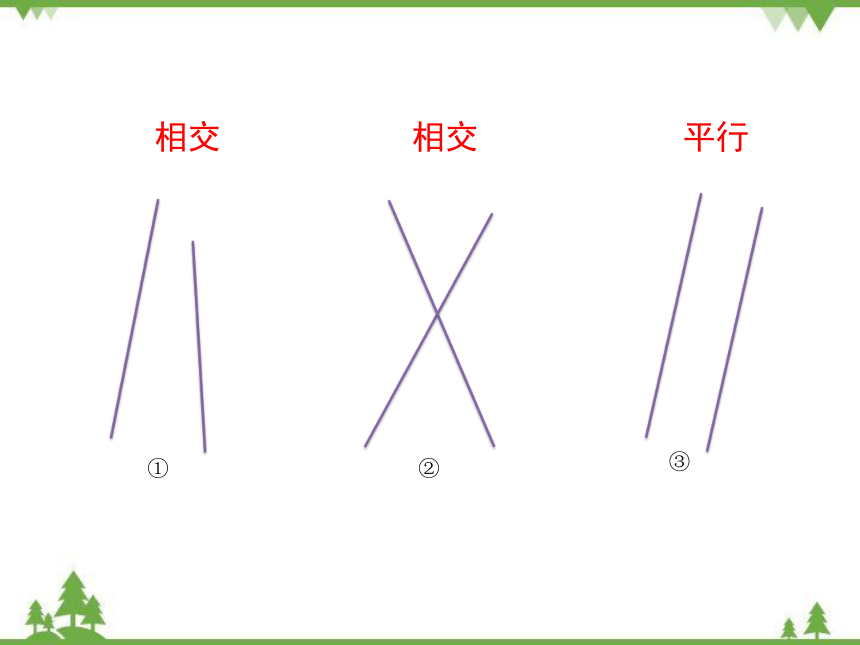
①
③
②
平行
相交
相交
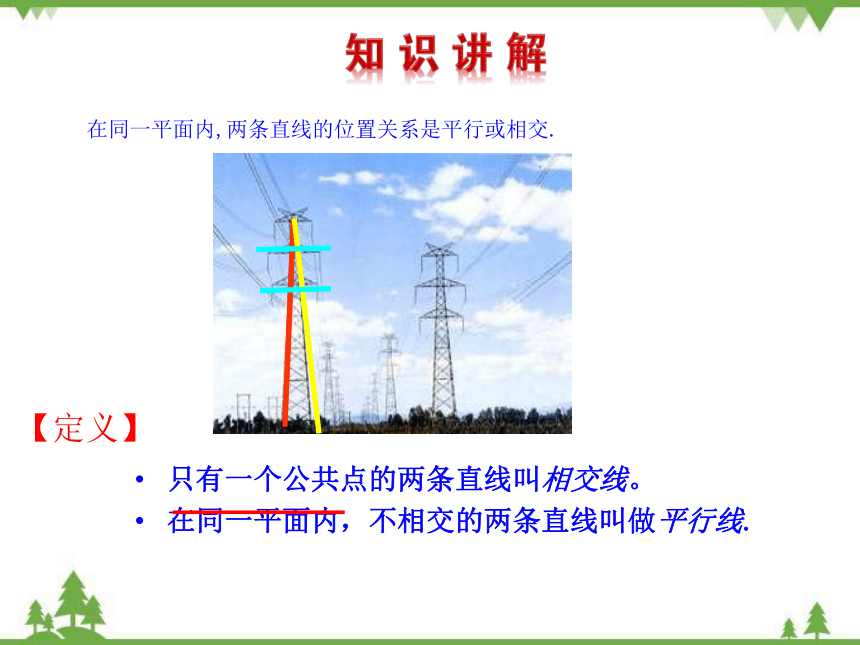
只有一个公共点的两条直线叫相交线。
在同一平面内,不相交的两条直线叫做平行线.
在同一平面内,两条直线的位置关系是平行或相交.
【定义】
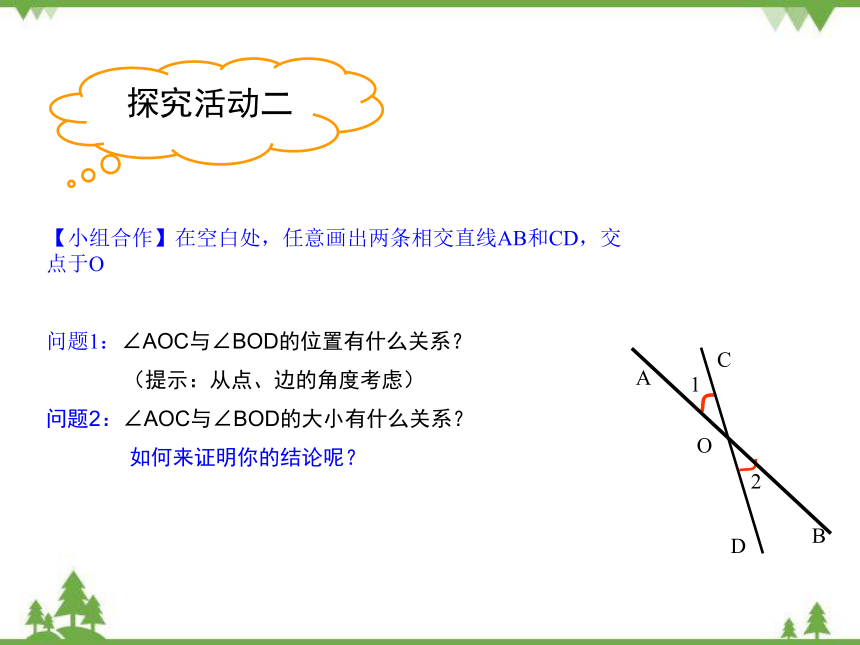
【小组合作】在空白处,任意画出两条相交直线AB和CD,交点于O
问题1:∠AOC与∠BOD的位置有什么关系?
(提示:从点、边的角度考虑)
问题2:∠AOC与∠BOD的大小有什么关系?
如何来证明你的结论呢?
1
2
A
C
D
B
O
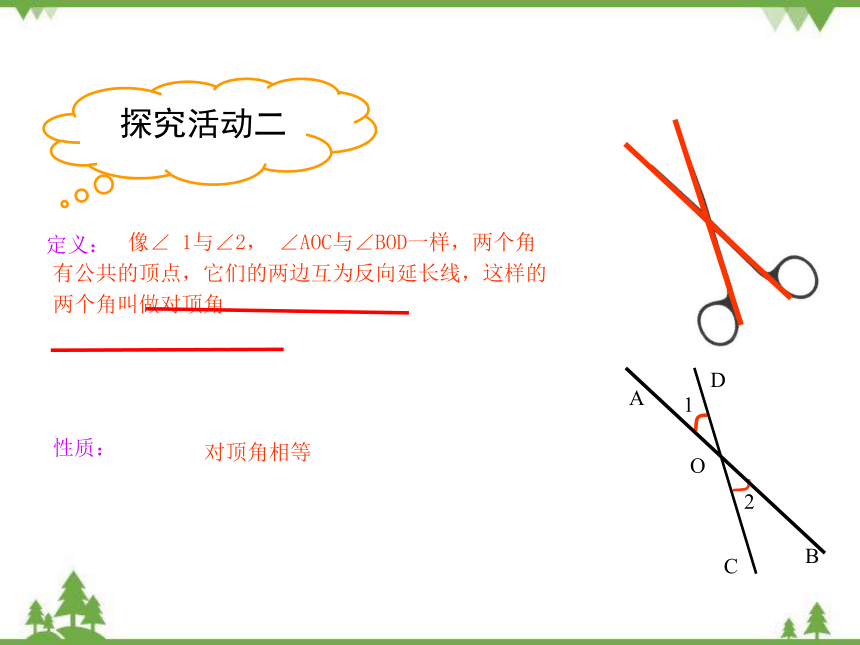
探究活动二
1
2
A
D
C
B
O
像∠ 1与∠2, ∠AOC与∠BOD一样,两个角有公共的顶点,它们的两边互为反向延长线,这样的两个角叫做对顶角.
对顶角相等
定义:
性质:
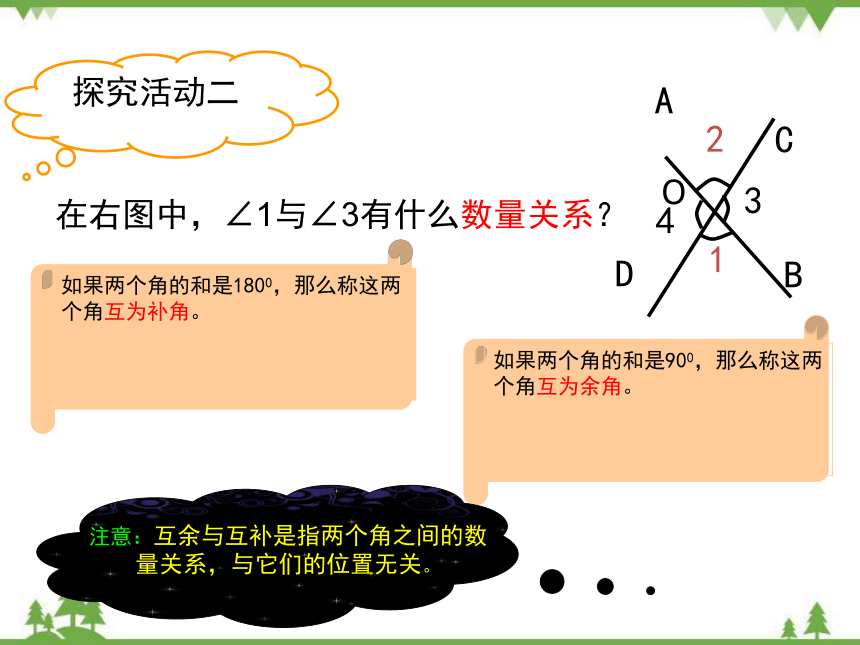
探究活动二
如果两个角的和是1800,那么称这两个角互为补角。
如果两个角的和是900,那么称这两个角互为余角。
注意:互余与互补是指两个角之间的数量关系,与它们的位置无关。
探究活动二
3
4
A
D
在右图中,∠1与∠3有什么数量关系?
2
1
O
B
C
1.下图中有对顶角吗?若有,请指出,若没有,请说明理由.
B
O
A
O
C
1
2
C'
B
A
C
1
2
C'
A
O
C
1
2
C'
O
(1)
(2)
(3)
B
A
1
3
2
4
B
D
C
O
(4)
【做一做】
2.如图直线AB、CD相交于一点,若∠2=35°,则∠1= ?∠4= ?
【做一做】
3
2
1
4
A
B
C
D
35°
145°
做一做
1.下列哪些角互为余角?
哪些角互为补角?
抢答题:老师编一道有关余角或者补角的题目,小组抢答。
问题2:下列说法正确的有 。(填序号)
①已知∠A=40 ,则∠A的余角等于50°
②若∠ 1+∠2=180 ,则∠1和∠2互为补角。
③若∠1+∠2+∠3=180 ,则∠1、∠2、∠3互补
④若∠A=40 26′,则∠A的补角=139 34′
⑤一个角的补角必为钝角。
①②④
做一做
探究活动三
【小组合作1】
(1)如图1,若直线AB与直线CD相交于点O,
则∠1与∠3都是∠2的 角,且大小 理由?
图1
(2)如图2,若∠AOB=∠COD=90°,
则∠ 1与∠ 3的大小关系如何?理由?
图2
1. ∠1与∠2大小有什么关系?为什么?
2. ∠AOD与∠BOC有什么关系?为什么?
3
4
1
2
B
A
O
E
C
D
如图,∠3=∠4,∠COE=∠DOE=90°
探究活动三
【小组合作2】
等角的余角相等
等角的补角相等
① ∠3=∠4
因为∠1=∠2
∠1+∠3=90°
∠2+∠4=90°
所以 ∠3=∠4
② ∠ABF=∠CBE
因为∠3=∠4
∠ABF+∠3=180°,∠CBE+∠4=180°
所以∠ABF=∠CBE
3
4
1
2
C
A
B
D
E
F
同角的余角相等
同角的补角相等
1.①因为∠1+∠2=90 ,∠3+∠2=90 ,所以∠1= ,理由是 ;
② 因为∠1+∠2=180 ,∠3+∠2=180 ,所以∠1= ,理由是 .
做一做
∠3
同角的余角相等
同角的补角相等
2.如图①中三角板,∠A是∠B的 。
变式训练:在①的基础上,做∠CDA=900。
则∠A的余角有哪几个?为什么?
C
A
B
C
A
B
D
做一做
①
(1)30°,70°与80°的和为平角,所以这三个角互补.( )
(2)一个角的余角必为锐角. ( )
(3)不相交的两条直线是平行线. ( )
(4)两角是否互补既与其大小有关又与其位置有关.( )
×
√
×
×
1.判断下列说法是否正确
【巩固拓展】
2.如图直线AB与CD交于点O, ∠EOD=900,回答下列问题:
∠AOC的余角是 ;补角是 ;对顶角是 。
C
A
B
D
O
E
【巩固拓展】
∠COE
∠COD和∠AOB
∠DOB
3.如图,直线AB,CD相交于点O,OE平分∠AOD,若∠BOD=100°,则∠AOE=_____.
【解析】∵∠AOD+∠BOD=180°,
∴∠AOD=180°-100°=80°.
∵OE平分∠AOD,
∴∠AOE= ∠AOD=40°
【巩固拓展】
40°
一、余角、补角、对顶角的概念:
二、余角、补角、对顶角的性质:
1. 和为90°的两个角称互为余角;
2. 和为180°的两个角称互为补角;
3. 有公共顶点,且两边互为反向延长线的两个角称为对顶角
1. 同角或等角的余角相等;
2. 同角或等角的补角相等;
3. 对顶角相等.
当 堂 检 测
1.如图,∠1与∠2是对顶角的是( )
2. 下列选项中,互为补角的一对角是( )
A. 20°与70° B. 35°与145°
C. 30°与160° D. 15°与145°
C
B
当 堂 检 测
C
3. 已知∠1+∠2=90°,∠3+∠4=180°,下列说法正确的是( )
A. ∠1是余角 B. ∠3是补角
C. ∠1是∠2的余角 D. ∠3和∠4都是补角
4. 若一个角的余角是30,则这个角的补角为 _______度
120
当 堂 检 测
5.已知∠COE = ∠BOD = ∠AOC = 90°,则图中与∠BOC相等的角为_________,与∠BOC互余的角为 _________
∠DOE
∠COD、∠BOA
1 两条直线的位置关系
a
·
·
A
B
1.从生活实例中抽象出相交线、平行线,概括出相交线、平行线的概念;
2.通过具体实例观察对顶角、余角、补角等的特征,认识对顶角、余角、补角概念;
3.探索并说出对顶角相等,同角(等角)的余角相等,同角(等角)的补角相等的性质,并能用这些性质解决一些简单问题。
①
③
②
平行
相交
相交
只有一个公共点的两条直线叫相交线。
在同一平面内,不相交的两条直线叫做平行线.
在同一平面内,两条直线的位置关系是平行或相交.
【定义】
【小组合作】在空白处,任意画出两条相交直线AB和CD,交点于O
问题1:∠AOC与∠BOD的位置有什么关系?
(提示:从点、边的角度考虑)
问题2:∠AOC与∠BOD的大小有什么关系?
如何来证明你的结论呢?
1
2
A
C
D
B
O
探究活动二
1
2
A
D
C
B
O
像∠ 1与∠2, ∠AOC与∠BOD一样,两个角有公共的顶点,它们的两边互为反向延长线,这样的两个角叫做对顶角.
对顶角相等
定义:
性质:
探究活动二
如果两个角的和是1800,那么称这两个角互为补角。
如果两个角的和是900,那么称这两个角互为余角。
注意:互余与互补是指两个角之间的数量关系,与它们的位置无关。
探究活动二
3
4
A
D
在右图中,∠1与∠3有什么数量关系?
2
1
O
B
C
1.下图中有对顶角吗?若有,请指出,若没有,请说明理由.
B
O
A
O
C
1
2
C'
B
A
C
1
2
C'
A
O
C
1
2
C'
O
(1)
(2)
(3)
B
A
1
3
2
4
B
D
C
O
(4)
【做一做】
2.如图直线AB、CD相交于一点,若∠2=35°,则∠1= ?∠4= ?
【做一做】
3
2
1
4
A
B
C
D
35°
145°
做一做
1.下列哪些角互为余角?
哪些角互为补角?
抢答题:老师编一道有关余角或者补角的题目,小组抢答。
问题2:下列说法正确的有 。(填序号)
①已知∠A=40 ,则∠A的余角等于50°
②若∠ 1+∠2=180 ,则∠1和∠2互为补角。
③若∠1+∠2+∠3=180 ,则∠1、∠2、∠3互补
④若∠A=40 26′,则∠A的补角=139 34′
⑤一个角的补角必为钝角。
①②④
做一做
探究活动三
【小组合作1】
(1)如图1,若直线AB与直线CD相交于点O,
则∠1与∠3都是∠2的 角,且大小 理由?
图1
(2)如图2,若∠AOB=∠COD=90°,
则∠ 1与∠ 3的大小关系如何?理由?
图2
1. ∠1与∠2大小有什么关系?为什么?
2. ∠AOD与∠BOC有什么关系?为什么?
3
4
1
2
B
A
O
E
C
D
如图,∠3=∠4,∠COE=∠DOE=90°
探究活动三
【小组合作2】
等角的余角相等
等角的补角相等
① ∠3=∠4
因为∠1=∠2
∠1+∠3=90°
∠2+∠4=90°
所以 ∠3=∠4
② ∠ABF=∠CBE
因为∠3=∠4
∠ABF+∠3=180°,∠CBE+∠4=180°
所以∠ABF=∠CBE
3
4
1
2
C
A
B
D
E
F
同角的余角相等
同角的补角相等
1.①因为∠1+∠2=90 ,∠3+∠2=90 ,所以∠1= ,理由是 ;
② 因为∠1+∠2=180 ,∠3+∠2=180 ,所以∠1= ,理由是 .
做一做
∠3
同角的余角相等
同角的补角相等
2.如图①中三角板,∠A是∠B的 。
变式训练:在①的基础上,做∠CDA=900。
则∠A的余角有哪几个?为什么?
C
A
B
C
A
B
D
做一做
①
(1)30°,70°与80°的和为平角,所以这三个角互补.( )
(2)一个角的余角必为锐角. ( )
(3)不相交的两条直线是平行线. ( )
(4)两角是否互补既与其大小有关又与其位置有关.( )
×
√
×
×
1.判断下列说法是否正确
【巩固拓展】
2.如图直线AB与CD交于点O, ∠EOD=900,回答下列问题:
∠AOC的余角是 ;补角是 ;对顶角是 。
C
A
B
D
O
E
【巩固拓展】
∠COE
∠COD和∠AOB
∠DOB
3.如图,直线AB,CD相交于点O,OE平分∠AOD,若∠BOD=100°,则∠AOE=_____.
【解析】∵∠AOD+∠BOD=180°,
∴∠AOD=180°-100°=80°.
∵OE平分∠AOD,
∴∠AOE= ∠AOD=40°
【巩固拓展】
40°
一、余角、补角、对顶角的概念:
二、余角、补角、对顶角的性质:
1. 和为90°的两个角称互为余角;
2. 和为180°的两个角称互为补角;
3. 有公共顶点,且两边互为反向延长线的两个角称为对顶角
1. 同角或等角的余角相等;
2. 同角或等角的补角相等;
3. 对顶角相等.
当 堂 检 测
1.如图,∠1与∠2是对顶角的是( )
2. 下列选项中,互为补角的一对角是( )
A. 20°与70° B. 35°与145°
C. 30°与160° D. 15°与145°
C
B
当 堂 检 测
C
3. 已知∠1+∠2=90°,∠3+∠4=180°,下列说法正确的是( )
A. ∠1是余角 B. ∠3是补角
C. ∠1是∠2的余角 D. ∠3和∠4都是补角
4. 若一个角的余角是30,则这个角的补角为 _______度
120
当 堂 检 测
5.已知∠COE = ∠BOD = ∠AOC = 90°,则图中与∠BOC相等的角为_________,与∠BOC互余的角为 _________
∠DOE
∠COD、∠BOA
同课章节目录
- 第五章 基本平面图形
- 1 线段、射线、 直线
- 2 比较线段的长短
- 3 角
- 4 角的比较
- 5 多边形和圆的初步认识
- 第六章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 零指数幂与负整数指数幂
- 5 整式的乘法
- 6 平方差公式
- 7 完全平方公式
- 8 整式的除法
- 第七章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第八章 数据的收集与整理
- 1 数据的收集
- 2 普查和抽样调查
- 3 数据的表示
- 4 统计图的选择
- 第九章 变量之间的关系
- 1 用表格表示变量之间的关系
- 2 用表达式表示变量之间的关系
- 3 用图象表示变量之间的关系
