2021-2022学年高一上学期数学北师大版(2019)必修第一册7.3频率与概率 课件(共34张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学北师大版(2019)必修第一册7.3频率与概率 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 19:50:15 | ||
图片预览











文档简介
(共34张PPT)
§7.2.3频率与概率
北师大(2019)必修1
琪
胡
学习目标
1.通过实例了解频率的概念.
2.通过试验寻求概率与频率的关系
3.结合实例,会用频率估计概率
数学素养
01
体验试验中总结规律的数学思想,提升数学抽象的素养.
数学抽象核心素养
02
数学建模核心素养
通过利用频率估计事件发生的概率,培养数学建模素养.
环节一
频率
什么是频率
思考
1.在日常生活中,我们怎样来衡量“很准”或“最有把握”
我们常用频率来量化“很准”或“最有把握”,例如在篮球比赛的统计中,有一项技术指标叫“投篮命中率”,是用来衡量运动员投篮准确性的.
什么是频率
频率
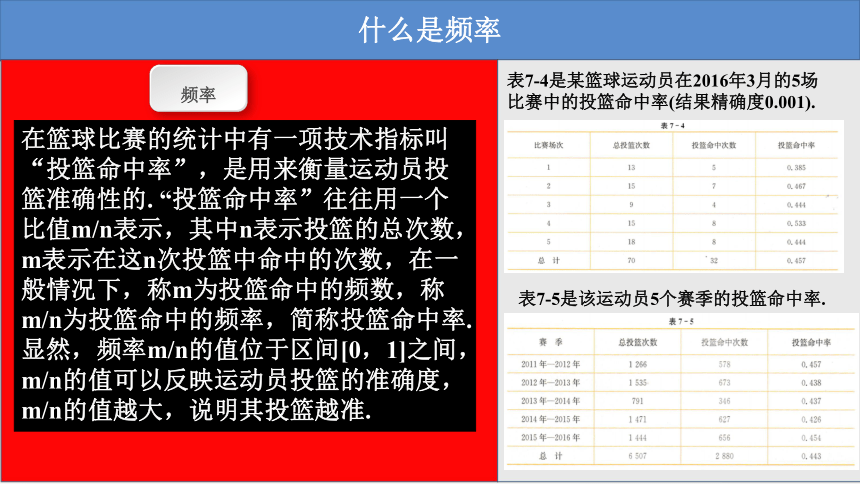
在篮球比赛的统计中有一项技术指标叫“投篮命中率”,是用来衡量运动员投篮准确性的. “投篮命中率”往往用一个比值m/n表示,其中n表示投篮的总次数,m表示在这n次投篮中命中的次数,在一般情况下,称m为投篮命中的频数,称m/n为投篮命中的频率,简称投篮命中率.显然,频率m/n的值位于区间[0,1]之间, m/n的值可以反映运动员投篮的准确度, m/n的值越大,说明其投篮越准.
表7-4是某篮球运动员在2016年3月的5场比赛中的投篮命中率(结果精确度0.001).
表7-5是该运动员5个赛季的投篮命中率.
什么是频率
频率
在篮球比赛的统计中有一项技术指标叫“投篮命中率”,是用来衡量运动员投篮准确性的. “投篮命中率”往往用一个比值m/n表示,其中n表示投篮的总次数,m表示在这n次投篮中命中的次数,在一般情况下,称m为投篮命中的频数,称m/n为投篮命中的频率,简称投篮命中率.显然,频率m/n的值位于区间[0,1]之间, m/n的值可以反映运动员投篮的准确度, m/n的值越大,说明其投篮越准.
数据分析
观察表7-4和表7-5,说说该运动员投篮命中的频率具有什么特征.
大量重复进行同一试验时,频率在某个常数附近摆动,即随机事件A发生的频率具有稳定性.
什么是频率
频率
当多次做抛掷一枚质地均匀的硬币,观察正面朝上的情况试验时,频率有什么特点
特点
与篮球运动员的投篮命中率类似,在抛掷硬币试验中,当抛掷次数较小时,由于受用力不均匀,桌面细微的凹凸不平等偶然因素的影响,使得正面朝上的频率并不稳定.但当抛掷次数逐渐增大时,试验逐渐摆脱了许多微小偶然因素的影响,而使正面朝上的频率有一种较好的稳定性,即正面朝上的频率稳定在0.5左右.
什么是频率
频率
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率通常会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,把这个常数叫作随机事件A的概率,记作P(A).显然,0≤P(A)≤1.我们通常用频率来估计概率.
频率与概率
事件发生的概率和事件发生的频率有什么区别和联系
概率是频率的稳定值,随着试验次数的增加,频率会越来越接近概率.频率本身是随机的,在试验前不能确定,概率是一个确定的常数,是客观存在的,在试验前已经确定与试验次数无关.
复习
1.什么是互斥事件
1.互斥事件的概念
(1)互斥事件:事件A与B___________发生,这时,我们称A,B为互斥事件.
(2)对立事件:互斥事件A,C中必有一个发生,这时,我们称A,C为对立事件,记作
C= 或A= .
思考
2.请从Venn图上直观判断出P(A∪B)与P(A),P(B)的大小关系
P(A)≤P(A∪B),P(B)≤P(A∪B).
环节二
频率与概率关系
频率与概率的关系
1.判断下列说法是否正确,正确的在它后面的括号里画“√”,错误的画“×”.
(1)概率是客观存在的一个确定的数.( √ )
(2)频率是客观存在的一个确定的数.( × )
(3)十次试验中,事件A发生了六次,其概率为0.6.( × )
(4)十次试验中,事件A发生了六次,其频率为0.6.( √ )
(5)随机事件A发生的频率可以用来估计随机事件A发生的概率.( √ )
辨析
(6)在大量重复试验中,概率是频率的稳定值.( √ )
(7)某次试验发生的频率越高,那么它的概率就越大.( × )
(8)概率随着频率的变化而变化.( × )
频率与概率的关系
辨析
2.下列说法:
①一个人打靶,打了10发子弹,有7发中靶.因此这个人中靶的概率为0.7;
②随机事件的频率与概率一定不相等;
③在条件不变的情况下,随机事件的概率不变;
④在一次试验结束后,随机事件的频率是变化的;
⑤任何事件都有概率.
其中正确的是 .(填序号)
解析:因为试验次数较少,此事件中靶的频率为0.7,不能说是概率,所以①错误;②在大量重复试验的情况下,频率稳定在某一常数附近,所以②错误;③概率是一个稳定值,不随试验次数的变化而变化,因此,在条件不变的情况下,概率不变,所以③正确;④频率随着试验的次数发生变化,但在一次试验结束后,频率是不变的,所以④错误;⑤事件包括必然事件、不可能事件、随机事件,它们都有概率,所以⑤正确.
答案:③⑤
频率与概率的关系
辨析
3.给出下列四个说法:
①设有一批产品,其次品率为0.05,则从中任取200件,必有10件是次品;
②做100次抛掷硬币的试验,结果51次出现正面朝上,因此,出
现正面朝上的概率是51/100;
③随机事件发生的频率就是这个随机事件发生的概率;
④抛掷一枚骰子100次,得点数是1的结果18次,则出现1点
的频率是9/50.
解析:①错误,次品率是大量产品的估计值,并不是针对200件产品来说的,所以任取200件,不一定有10件是次品;②③混淆了频率与概率的概念;④正确.
答案:④
频率与概率的关系
辨析
4.(1)下列说法正确的是( )
A.由生物学知道生男、生女的概率均约为0.5,一对夫妇先后生两小孩,则一定为一男一女
B.一次摸奖活动中,中奖概率为0.2,则摸5张票,一定有一张中奖
C.10张票中有1张奖票,10人去摸,谁先摸则谁摸到奖票的可能性大
D.10张票中有1张奖票,10人去摸,无论谁先摸,摸到奖票的概率都是0.1
D
【解析】(1)一对夫妇生两小孩可能是(男,男),(男,女),(女,男),(女,女),所以A不正确;中奖概率为0.2是说中奖的可能性为0.2,当摸5张票时,可能都中奖,也可能中一张、两张、三张、四张,或者都不中奖,所以B不正确;10张票中有1张奖票,10人去摸,每人摸到的可能性是相同的,即无论谁先摸,摸到奖票的概率都是0.1,所以C不正确;D正确.
频率与概率的关系
辨析
5.某工厂生产的产品合格率是99.99%,这说明( )
A.该厂生产的10 000件产品中不合格的产品一定有1件
B.该厂生产的10 000件产品中合格的产品一定有9 999件
C.合格率是99.99%,说明该厂生产的10 000件产品中没有不合格产品
D.该厂生产的产品合格的可能性是99.99%
D
合格率是99.99%,是指该工厂生产的每件产品合格的可能性大小,即合格的概率.
频率与概率的关系
辨析
6.在天气预报中,有“降水概率预报”.例如,预报“明天降水概率为85%”,这是指( )
A.明天该地区有85%的地区降水,其他15%地区不降水
B.明天该地区约有85%的时间降水,其他时间不降水
C.气象台的专家中,有85%的人认为会降水,另外15%的专家认为不降水
D.明天该地区降水的可能性为85%
概率的本质含义是事件发生的可能性大小,因此D正确.
规律方法提炼
1.概率意义下的“可能性”是大量随机现象的客观规律,与我们平时所说的“可能”“估计”是不同的,也就是说,单独一次结果的不肯定性与积累结果的规律性,才是概率意义下的“可能性”,而日常生活中的“可能”“估计”侧重于某次的偶然性.
2.概率与频率关系:对于一个事件而言,概率是一个常数,而频率则随着试验次数的变化而变化,试验次数越多,频率就越接近于事件的概率.
环节三
用频率估计概率
用频率估计概率
例1.某公司在过去几年内使用某种型号的灯管1 000支,该公司对这些灯管的使用寿命(单位:h)进行了统计,统计结果如下表所示.
(1)将各组的频率填入表中;
(2)根据上述统计结果,计算灯管使用寿命不足1 500 h的频率;
(3)估计灯管使用寿命不足1 500 h的概率.
用频率估计概率
用频率估计概率
例1.某公司在过去几年内使用某种型号的灯管1 000支,该公司对这些灯管的使用寿命(单位:h)进行了统计,统计结果如下表所示.
(1)将各组的频率填入表中;
(2)根据上述统计结果,计算灯管使用寿命不足1 500 h的频率;
(3)估计灯管使用寿命不足1 500 h的概率.
(2)样本中寿命不足1 500 h的频数是48+121+208+223=600,
所以样本中寿命不足1 500 h的频率是=0.6.
(3)估计灯管使用寿命不足1 500 h的概率是0.6.
用频率估计概率
例2.下面是某批乒乓球质量检查结果表:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率
(1)在上表中填上优等品出现的频率;
(2)估计该批乒乓球优等品的概率是多少?
(2)从表中数据可以看出,这批乒乓球优等品的概率是0.95.
用频率估计概率
例3.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如表:
上年度出险次数 0 1 2 3 4 ≥5
保费 0.85a a 1.25a 1.5a 1.75a 2a
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 0 1 2 3 4 ≥5
频数 60 50 30 30 20 10
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
用频率估计概率
【解析】(1)事件A发生当且仅当一年内出险次数小于2.由所给数据知,一年内出险次数小于2的频率为 =0.55,故P(A)的估计值为0.55.
(2)事件B发生当且仅当一年内出险次数大于1且小于4.
由所给数据知,一年内出险次数大于1且小于4的频率为 =0.3,
故P(B)的估计值为0.3.
(3)由所给数据得
保费 0.85a a 1.25a 1.5a 1.75a 2a
频率 0.30 0.25 0.15 0.15 0.10 0.05
调查的200名续保人的平均保费为
0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=
1.192 5a(元).
因此续保人本年度平均保费的估计值为1.192 5a(元).
环节五
当堂检测
检测
1.下列正确的结论是 ( )
A.频率是客观存在的,与试验次数无关
B.如P(A)=0.999,则A为必然事件
C.灯泡的合格率是99%,从一批灯泡中任取一个是合格品的可能性为99%
D.如P(A)=0.001,则A为不可能事件
【解析】选C.频率是由试验的次数决定的,所以选项A错误;因为必然事件的概率为1,所以可排除选项B;因为不可能事件的概率为0,所以可排除选项D;根据概率的定义可知,灯泡的合格率是99%,从一批灯泡中任取一个是合格品的可能性为99%.
检测
2. .设某厂产品的次品率为3%,估计该厂8 000件产品中次品的件数为 ( )
A.3 B.160 C.240 D.7 480
【解析】选C.因为该厂的次品率为3%,所以该厂8 000件产品的次品数为8 000×3%=240.
检测
3如果袋中装有数量差别很大而大小相同的白球和黄球(只是颜色不同)若干个,从中任取一球,取了10次有7次是白球,估计袋中数量最多的是 球.
【解析】取了10次有7次是白球,则取出白球的频率是0.7,估计其概率是0.7,那么取出黄球的概率约是0.3,取出白球的概率大于取出黄球的概率,所以估计袋中数量最多的是白球.
答案:白
检测
4.某中学为了了解初中部学生的佩戴胸卡的情况,在学校随机抽取初中部的150名学生,其中有60名佩戴胸卡.第二次检查,调查了初中部的所有学生,有500名学生佩戴胸卡.据此估计该中学初中部一共有多少名学生.
解:设初中部有n名学生,依题意得60/150=500/n,解得n=1 250.所以该中学初中部共有学生大约1 250名.
检测
5.我国古代数学名著《九章算术》中有“米谷粒分”题:粮仓开仓收粮,有人送来米1 536石,验得米内夹谷,抽样取米一把,数得256粒内夹谷18粒,则这批米内夹谷约为( )
A.108石 B.169石 C.237石 D.338石
解析:∵256粒内夹谷18粒,∴米中含谷的频率为18/256=9/128,∴1 536石中夹谷约为1 536×9/128=12×9=108(石).故选A.
课堂小结
1.核心要点
1.通过实例了解频率的概念.
2.通过试验寻求概率与频率的关系
3.结合实例,会用频率估计概率
2.数学素养
抽象素养和建模素养
胡琪老师制作
§7.2.3频率与概率
北师大(2019)必修1
琪
胡
学习目标
1.通过实例了解频率的概念.
2.通过试验寻求概率与频率的关系
3.结合实例,会用频率估计概率
数学素养
01
体验试验中总结规律的数学思想,提升数学抽象的素养.
数学抽象核心素养
02
数学建模核心素养
通过利用频率估计事件发生的概率,培养数学建模素养.
环节一
频率
什么是频率
思考
1.在日常生活中,我们怎样来衡量“很准”或“最有把握”
我们常用频率来量化“很准”或“最有把握”,例如在篮球比赛的统计中,有一项技术指标叫“投篮命中率”,是用来衡量运动员投篮准确性的.
什么是频率
频率
在篮球比赛的统计中有一项技术指标叫“投篮命中率”,是用来衡量运动员投篮准确性的. “投篮命中率”往往用一个比值m/n表示,其中n表示投篮的总次数,m表示在这n次投篮中命中的次数,在一般情况下,称m为投篮命中的频数,称m/n为投篮命中的频率,简称投篮命中率.显然,频率m/n的值位于区间[0,1]之间, m/n的值可以反映运动员投篮的准确度, m/n的值越大,说明其投篮越准.
表7-4是某篮球运动员在2016年3月的5场比赛中的投篮命中率(结果精确度0.001).
表7-5是该运动员5个赛季的投篮命中率.
什么是频率
频率
在篮球比赛的统计中有一项技术指标叫“投篮命中率”,是用来衡量运动员投篮准确性的. “投篮命中率”往往用一个比值m/n表示,其中n表示投篮的总次数,m表示在这n次投篮中命中的次数,在一般情况下,称m为投篮命中的频数,称m/n为投篮命中的频率,简称投篮命中率.显然,频率m/n的值位于区间[0,1]之间, m/n的值可以反映运动员投篮的准确度, m/n的值越大,说明其投篮越准.
数据分析
观察表7-4和表7-5,说说该运动员投篮命中的频率具有什么特征.
大量重复进行同一试验时,频率在某个常数附近摆动,即随机事件A发生的频率具有稳定性.
什么是频率
频率
当多次做抛掷一枚质地均匀的硬币,观察正面朝上的情况试验时,频率有什么特点
特点
与篮球运动员的投篮命中率类似,在抛掷硬币试验中,当抛掷次数较小时,由于受用力不均匀,桌面细微的凹凸不平等偶然因素的影响,使得正面朝上的频率并不稳定.但当抛掷次数逐渐增大时,试验逐渐摆脱了许多微小偶然因素的影响,而使正面朝上的频率有一种较好的稳定性,即正面朝上的频率稳定在0.5左右.
什么是频率
频率
在相同条件下,大量重复进行同一试验时,随机事件A发生的频率通常会在某个常数附近摆动,即随机事件A发生的频率具有稳定性.这时,把这个常数叫作随机事件A的概率,记作P(A).显然,0≤P(A)≤1.我们通常用频率来估计概率.
频率与概率
事件发生的概率和事件发生的频率有什么区别和联系
概率是频率的稳定值,随着试验次数的增加,频率会越来越接近概率.频率本身是随机的,在试验前不能确定,概率是一个确定的常数,是客观存在的,在试验前已经确定与试验次数无关.
复习
1.什么是互斥事件
1.互斥事件的概念
(1)互斥事件:事件A与B___________发生,这时,我们称A,B为互斥事件.
(2)对立事件:互斥事件A,C中必有一个发生,这时,我们称A,C为对立事件,记作
C= 或A= .
思考
2.请从Venn图上直观判断出P(A∪B)与P(A),P(B)的大小关系
P(A)≤P(A∪B),P(B)≤P(A∪B).
环节二
频率与概率关系
频率与概率的关系
1.判断下列说法是否正确,正确的在它后面的括号里画“√”,错误的画“×”.
(1)概率是客观存在的一个确定的数.( √ )
(2)频率是客观存在的一个确定的数.( × )
(3)十次试验中,事件A发生了六次,其概率为0.6.( × )
(4)十次试验中,事件A发生了六次,其频率为0.6.( √ )
(5)随机事件A发生的频率可以用来估计随机事件A发生的概率.( √ )
辨析
(6)在大量重复试验中,概率是频率的稳定值.( √ )
(7)某次试验发生的频率越高,那么它的概率就越大.( × )
(8)概率随着频率的变化而变化.( × )
频率与概率的关系
辨析
2.下列说法:
①一个人打靶,打了10发子弹,有7发中靶.因此这个人中靶的概率为0.7;
②随机事件的频率与概率一定不相等;
③在条件不变的情况下,随机事件的概率不变;
④在一次试验结束后,随机事件的频率是变化的;
⑤任何事件都有概率.
其中正确的是 .(填序号)
解析:因为试验次数较少,此事件中靶的频率为0.7,不能说是概率,所以①错误;②在大量重复试验的情况下,频率稳定在某一常数附近,所以②错误;③概率是一个稳定值,不随试验次数的变化而变化,因此,在条件不变的情况下,概率不变,所以③正确;④频率随着试验的次数发生变化,但在一次试验结束后,频率是不变的,所以④错误;⑤事件包括必然事件、不可能事件、随机事件,它们都有概率,所以⑤正确.
答案:③⑤
频率与概率的关系
辨析
3.给出下列四个说法:
①设有一批产品,其次品率为0.05,则从中任取200件,必有10件是次品;
②做100次抛掷硬币的试验,结果51次出现正面朝上,因此,出
现正面朝上的概率是51/100;
③随机事件发生的频率就是这个随机事件发生的概率;
④抛掷一枚骰子100次,得点数是1的结果18次,则出现1点
的频率是9/50.
解析:①错误,次品率是大量产品的估计值,并不是针对200件产品来说的,所以任取200件,不一定有10件是次品;②③混淆了频率与概率的概念;④正确.
答案:④
频率与概率的关系
辨析
4.(1)下列说法正确的是( )
A.由生物学知道生男、生女的概率均约为0.5,一对夫妇先后生两小孩,则一定为一男一女
B.一次摸奖活动中,中奖概率为0.2,则摸5张票,一定有一张中奖
C.10张票中有1张奖票,10人去摸,谁先摸则谁摸到奖票的可能性大
D.10张票中有1张奖票,10人去摸,无论谁先摸,摸到奖票的概率都是0.1
D
【解析】(1)一对夫妇生两小孩可能是(男,男),(男,女),(女,男),(女,女),所以A不正确;中奖概率为0.2是说中奖的可能性为0.2,当摸5张票时,可能都中奖,也可能中一张、两张、三张、四张,或者都不中奖,所以B不正确;10张票中有1张奖票,10人去摸,每人摸到的可能性是相同的,即无论谁先摸,摸到奖票的概率都是0.1,所以C不正确;D正确.
频率与概率的关系
辨析
5.某工厂生产的产品合格率是99.99%,这说明( )
A.该厂生产的10 000件产品中不合格的产品一定有1件
B.该厂生产的10 000件产品中合格的产品一定有9 999件
C.合格率是99.99%,说明该厂生产的10 000件产品中没有不合格产品
D.该厂生产的产品合格的可能性是99.99%
D
合格率是99.99%,是指该工厂生产的每件产品合格的可能性大小,即合格的概率.
频率与概率的关系
辨析
6.在天气预报中,有“降水概率预报”.例如,预报“明天降水概率为85%”,这是指( )
A.明天该地区有85%的地区降水,其他15%地区不降水
B.明天该地区约有85%的时间降水,其他时间不降水
C.气象台的专家中,有85%的人认为会降水,另外15%的专家认为不降水
D.明天该地区降水的可能性为85%
概率的本质含义是事件发生的可能性大小,因此D正确.
规律方法提炼
1.概率意义下的“可能性”是大量随机现象的客观规律,与我们平时所说的“可能”“估计”是不同的,也就是说,单独一次结果的不肯定性与积累结果的规律性,才是概率意义下的“可能性”,而日常生活中的“可能”“估计”侧重于某次的偶然性.
2.概率与频率关系:对于一个事件而言,概率是一个常数,而频率则随着试验次数的变化而变化,试验次数越多,频率就越接近于事件的概率.
环节三
用频率估计概率
用频率估计概率
例1.某公司在过去几年内使用某种型号的灯管1 000支,该公司对这些灯管的使用寿命(单位:h)进行了统计,统计结果如下表所示.
(1)将各组的频率填入表中;
(2)根据上述统计结果,计算灯管使用寿命不足1 500 h的频率;
(3)估计灯管使用寿命不足1 500 h的概率.
用频率估计概率
用频率估计概率
例1.某公司在过去几年内使用某种型号的灯管1 000支,该公司对这些灯管的使用寿命(单位:h)进行了统计,统计结果如下表所示.
(1)将各组的频率填入表中;
(2)根据上述统计结果,计算灯管使用寿命不足1 500 h的频率;
(3)估计灯管使用寿命不足1 500 h的概率.
(2)样本中寿命不足1 500 h的频数是48+121+208+223=600,
所以样本中寿命不足1 500 h的频率是=0.6.
(3)估计灯管使用寿命不足1 500 h的概率是0.6.
用频率估计概率
例2.下面是某批乒乓球质量检查结果表:
抽取球数 50 100 200 500 1 000 2 000
优等品数 45 92 194 470 954 1 902
优等品出现的频率
(1)在上表中填上优等品出现的频率;
(2)估计该批乒乓球优等品的概率是多少?
(2)从表中数据可以看出,这批乒乓球优等品的概率是0.95.
用频率估计概率
例3.某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如表:
上年度出险次数 0 1 2 3 4 ≥5
保费 0.85a a 1.25a 1.5a 1.75a 2a
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 0 1 2 3 4 ≥5
频数 60 50 30 30 20 10
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
用频率估计概率
【解析】(1)事件A发生当且仅当一年内出险次数小于2.由所给数据知,一年内出险次数小于2的频率为 =0.55,故P(A)的估计值为0.55.
(2)事件B发生当且仅当一年内出险次数大于1且小于4.
由所给数据知,一年内出险次数大于1且小于4的频率为 =0.3,
故P(B)的估计值为0.3.
(3)由所给数据得
保费 0.85a a 1.25a 1.5a 1.75a 2a
频率 0.30 0.25 0.15 0.15 0.10 0.05
调查的200名续保人的平均保费为
0.85a×0.30+a×0.25+1.25a×0.15+1.5a×0.15+1.75a×0.10+2a×0.05=
1.192 5a(元).
因此续保人本年度平均保费的估计值为1.192 5a(元).
环节五
当堂检测
检测
1.下列正确的结论是 ( )
A.频率是客观存在的,与试验次数无关
B.如P(A)=0.999,则A为必然事件
C.灯泡的合格率是99%,从一批灯泡中任取一个是合格品的可能性为99%
D.如P(A)=0.001,则A为不可能事件
【解析】选C.频率是由试验的次数决定的,所以选项A错误;因为必然事件的概率为1,所以可排除选项B;因为不可能事件的概率为0,所以可排除选项D;根据概率的定义可知,灯泡的合格率是99%,从一批灯泡中任取一个是合格品的可能性为99%.
检测
2. .设某厂产品的次品率为3%,估计该厂8 000件产品中次品的件数为 ( )
A.3 B.160 C.240 D.7 480
【解析】选C.因为该厂的次品率为3%,所以该厂8 000件产品的次品数为8 000×3%=240.
检测
3如果袋中装有数量差别很大而大小相同的白球和黄球(只是颜色不同)若干个,从中任取一球,取了10次有7次是白球,估计袋中数量最多的是 球.
【解析】取了10次有7次是白球,则取出白球的频率是0.7,估计其概率是0.7,那么取出黄球的概率约是0.3,取出白球的概率大于取出黄球的概率,所以估计袋中数量最多的是白球.
答案:白
检测
4.某中学为了了解初中部学生的佩戴胸卡的情况,在学校随机抽取初中部的150名学生,其中有60名佩戴胸卡.第二次检查,调查了初中部的所有学生,有500名学生佩戴胸卡.据此估计该中学初中部一共有多少名学生.
解:设初中部有n名学生,依题意得60/150=500/n,解得n=1 250.所以该中学初中部共有学生大约1 250名.
检测
5.我国古代数学名著《九章算术》中有“米谷粒分”题:粮仓开仓收粮,有人送来米1 536石,验得米内夹谷,抽样取米一把,数得256粒内夹谷18粒,则这批米内夹谷约为( )
A.108石 B.169石 C.237石 D.338石
解析:∵256粒内夹谷18粒,∴米中含谷的频率为18/256=9/128,∴1 536石中夹谷约为1 536×9/128=12×9=108(石).故选A.
课堂小结
1.核心要点
1.通过实例了解频率的概念.
2.通过试验寻求概率与频率的关系
3.结合实例,会用频率估计概率
2.数学素养
抽象素养和建模素养
胡琪老师制作
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
