2021-2022学年度高中数学新课标人版A版必修3课件 3.3.1几何概型 (共27张PPT)
文档属性
| 名称 | 2021-2022学年度高中数学新课标人版A版必修3课件 3.3.1几何概型 (共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:01:39 | ||
图片预览






文档简介
(共27张PPT)
古典概型的两个基本特点:
(1)每个基本事件出现的可能性相等;
(2)试验中所有可能出现的基本事件只有有限个.
前面我们学习了古典概型的特点以及概率计算公式和随机数模拟古典概型试验
对于有限的基本事件,我们了可以通过试验方法计算频率得到概率的近似估计概率,对于满足古典概型的概率问题也可以通过古典概型的概率计算公式来计算概率
随着概率论的发展,人们就注意到,单纯的考虑有限个等可能事件的随机试验是不够的,还必须考虑有无限多个的试验结果的情况.
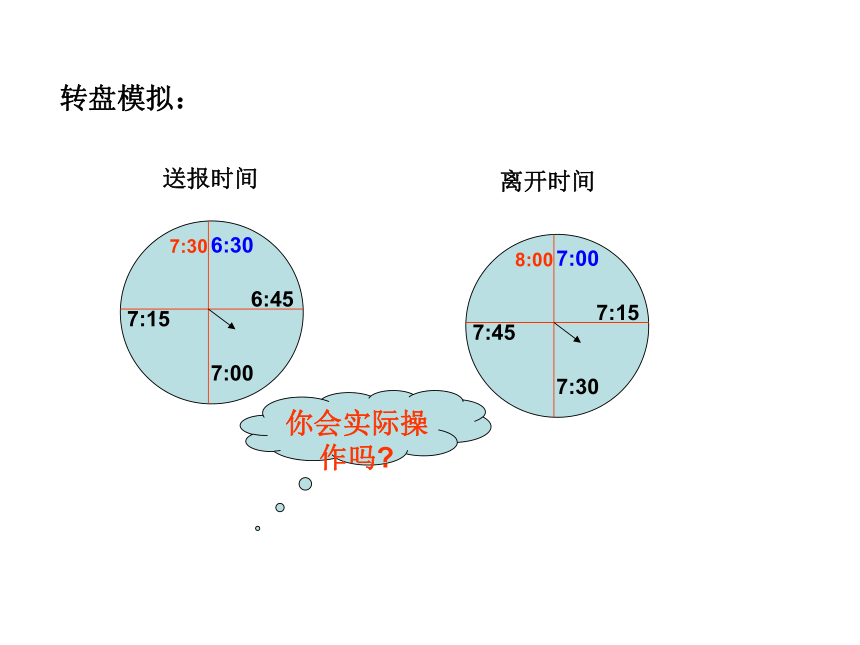
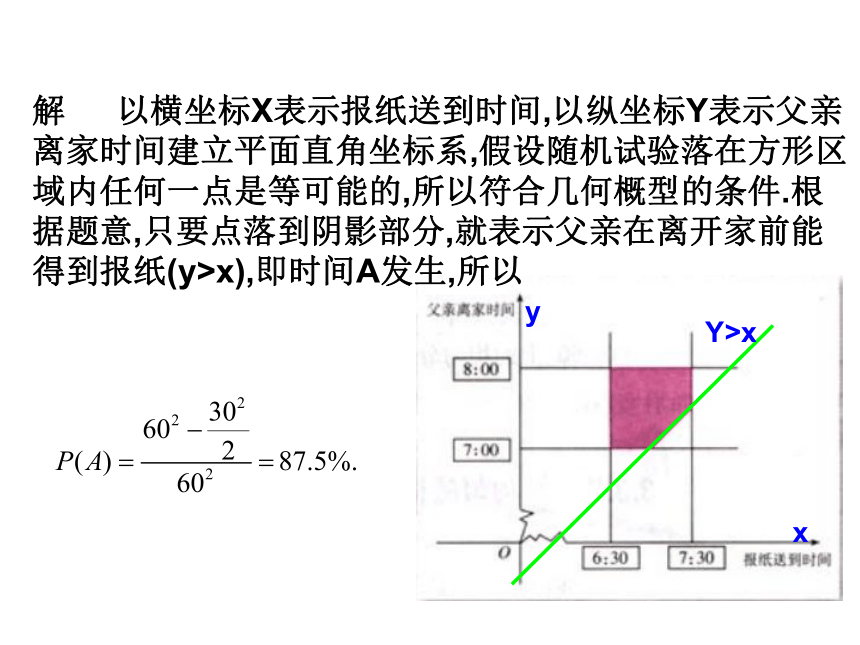
例1. 送报人可能在早上6:30-7:30之间把报纸送到你家,你父亲离开家的时间在7:00-8:00之间,问你父亲离开家前能得到报纸(称为事件A)的概率是多少
1.可否利用古典概率来计算其概率
2.可否利用随机数来模拟古典概率
3.你能否再设计一种方法来模拟这一实验
虽然事件发生的概率是随机等可能的,但事件A和总体事件的个数都无法计算出来,因此古典概率很难将它算出
利用随机数模拟方法应该可以实现,关键是怎样构造数字代表的事件,构造起来比较麻烦,利于我们通过均匀随机数法随机产生1次从630~700 的数,产生一次700~800的数,前一个表示送报时间,后一个代表离开时间,多产生几组,就可以模拟时间发生的概率
转盘模拟:
6:30
6:45
7:00
7:15
7:30
7:00
7:15
7:30
7:45
8:00
送报时间
离开时间
你会实际操作吗
对于上面的方式,我们来模拟它们的得到的概率操作过程都是很复杂的,几何概型就是专门来解决这类“无限事件”的概率问题
在解决这个问题之前,我们首先来看另外一个试验:
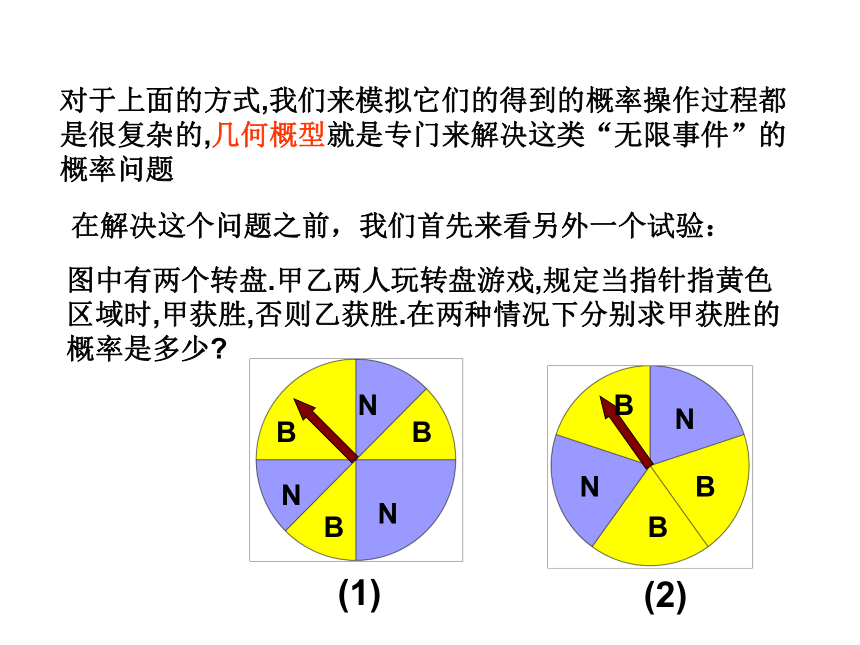
图中有两个转盘.甲乙两人玩转盘游戏,规定当指针指黄色区域时,甲获胜,否则乙获胜.在两种情况下分别求甲获胜的概率是多少
(1)
N
B
N
N
B
B
(2)
N
N
B
B
B
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例.则称这样的概率模型为几何概率模型(geometric models of probability),简称几何概型.
则上题中(1)、(2)“甲获胜”的概率分别为1/2,3/5
Y>x
y
x
解 以横坐标X表示报纸送到时间,以纵坐标Y表示父亲离家时间建立平面直角坐标系,假设随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.根据题意,只要点落到阴影部分,就表示父亲在离开家前能
得到报纸(y>x),即时间A发生,所以
两种方法得到的结果相同吗?
对于复杂的实际问题,解题的关键是要建立概率模型,找出随机事件与所有基本事件相对应的几何区域,把问题转化为几何问题,利用几何模型概率公式求解
2.某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.
1.两人相约于 7 时到 8 时在公园见面,先到者等候 20 分钟就可离去,求两人能够见面的概率。
几何概型的特点
试验中所有可能出现的结果(基本事件)有无限多个;
每个基本事件出现的可能性相等
古典概型与几何概型的区别
相同:两者基本事件发生的可能性都是相等的;
不同:古典概型要求基本事件有有限个,几何概型要求基本事件有无限多个。
解. 以 7 点为坐标原点,
小时为单位。x,y 分别表示
两人到达的时间,( x,y )
构成边长为 60的正方形S,
显然这是一个几何概率问题。
60
60
o
x
y
S
20
20
他们能见面应满足 | x – y | ≤ 20 ,因此,
A
x – y = – 20
x – y = 20
p = ————— = 1 – —— = 5/9 。
A 的面积
S 的面积
4
9
弄清π是无理数这件事可能是根本没有实际用处的 但是如果我们能弄清楚 那么肯定就不能容忍不去设法把它弄清楚——E·C·Titchmarsh
它们从不同的方式计算着π的值,
1.实验时期:过实验对 π 值进行估算
2.几何法时期:割圆术
3.分析法时期 :
4.计算机时期 :
其中比较有名的就是利用随机试验来估计π的值.
Buffoon,Georges Louis
蒲丰
(1707─1788)
利用蒙特卡罗(Monte Carlo)法进行计算机模拟.
蒲丰投针试验
例3 1777年,法国科学家蒲丰(Buffon)提出了投针
试验问题.平面上画有等距离为a(a>0)的一些平行直
线,现向此平面任意投掷一根长为b( b针与某一平行直线相交的概率.
解
由投掷的任意性可知,
这是一个几何概型问题.
投针可能事件与相交事件:
蒲丰投针试验的应用及意义
历史上一些学者的计算结果(直线距离a=1)
3.1795
859
2520
0.5419
1925
Reina
3.1415929
1808
3408
0.83
1901
Lazzerini
3.1595
489
1030
0.75
1884
Fox
3.137
382
600
1.0
1860
De Morgan
3.1554
1218
3204
0.6
1855
Smith
3.1596
2532
5000
0.8
1850
Wolf
相交次数
投掷次数
针长
时间
试验者
课本例三和例4提供了两种计算面积的方法,请大家参考后,解决下列问题:
3.一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒。当你到达路口时,看见下列三种情况的 概率各是多少?
(1)红灯;(2)黄灯;(3)不是红灯。
4.假设车站每隔 10 分钟发一班车,随机到达车站,问等车时间不超过 3 分钟的概率 ?
5.国家安全机关监听录音机记录了两个间谍的谈话,发现长30min的磁带上,从开始30s处起,有10s长的一段内容包含间谍犯罪的信息.后来发现,这段谈话的部分被某工作人员擦掉了,该工作人员声称他完全是无意中按错了键,使从此后起往后的所有内容都被擦掉了.那么由于按错了键使含有犯罪内容的谈话被部分或全部擦掉的概率有多大?
6.山姆的意大利馅饼屋中设有一个投镖靶 该靶为正方形板.边长为18厘米,挂于前门附近的墙上,顾客花两角伍分的硬币便可投一镖并可有机会赢得一种意大利馅饼中的一个,投镖靶中画有三个同心圆,圆心在靶的中心,当投镖击中半径为1厘米的最内层圆域时.可得到一个大馅饼;当击中半径为1厘米到2厘米之间的环域时,可得到一个中馅饼;如果击中半径为2厘米到3厘米之间的环域时,可得到一个小馅饼,如果击中靶上的其他部分,则得不到馅饼,我们假设每一个顾客都能投镖中靶,并假设每个圆的周边线没有宽度,即每个投镖不会击中线上,试求一顾客将嬴得: (a)一张大馅饼, (b)一张中馅饼, (c)一张小馅饼, (d)没得到馅饼的概率
7.两艘船都要停靠同一泊位,它们可能在一昼夜的任何时刻到达,甲乙两船停靠泊位的时间分别为4小时和2小时,求有一艘船停靠泊位时间必须等待一段时间的概率
对,在几何概型中,如果随机事件所在区域是一个单点,由于单点的长度、面积、体积为0,则它出现的概率为0,但它不是不可能事件;如果一个随机事件所在区域是全部区域扣除一个单点,则它出现的概率为1,但它不是必然事件
思考:“必然事件的概率为1,但概率为1的事件不一定是必然事件。”这种说法对吗?为什么
例如某人7:00~8:00上班,求它刚好不在7:30上班的概率,很明显是一个几何概型,其概率为1,但他7:30上班的确有可能,这就不是必然事件了
7:00 7:30 8:00
几何概型
特点
概率计算公式
均匀随机数
随机模拟方法
古典概型的两个基本特点:
(1)每个基本事件出现的可能性相等;
(2)试验中所有可能出现的基本事件只有有限个.
前面我们学习了古典概型的特点以及概率计算公式和随机数模拟古典概型试验
对于有限的基本事件,我们了可以通过试验方法计算频率得到概率的近似估计概率,对于满足古典概型的概率问题也可以通过古典概型的概率计算公式来计算概率
随着概率论的发展,人们就注意到,单纯的考虑有限个等可能事件的随机试验是不够的,还必须考虑有无限多个的试验结果的情况.
例1. 送报人可能在早上6:30-7:30之间把报纸送到你家,你父亲离开家的时间在7:00-8:00之间,问你父亲离开家前能得到报纸(称为事件A)的概率是多少
1.可否利用古典概率来计算其概率
2.可否利用随机数来模拟古典概率
3.你能否再设计一种方法来模拟这一实验
虽然事件发生的概率是随机等可能的,但事件A和总体事件的个数都无法计算出来,因此古典概率很难将它算出
利用随机数模拟方法应该可以实现,关键是怎样构造数字代表的事件,构造起来比较麻烦,利于我们通过均匀随机数法随机产生1次从630~700 的数,产生一次700~800的数,前一个表示送报时间,后一个代表离开时间,多产生几组,就可以模拟时间发生的概率
转盘模拟:
6:30
6:45
7:00
7:15
7:30
7:00
7:15
7:30
7:45
8:00
送报时间
离开时间
你会实际操作吗
对于上面的方式,我们来模拟它们的得到的概率操作过程都是很复杂的,几何概型就是专门来解决这类“无限事件”的概率问题
在解决这个问题之前,我们首先来看另外一个试验:
图中有两个转盘.甲乙两人玩转盘游戏,规定当指针指黄色区域时,甲获胜,否则乙获胜.在两种情况下分别求甲获胜的概率是多少
(1)
N
B
N
N
B
B
(2)
N
N
B
B
B
如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例.则称这样的概率模型为几何概率模型(geometric models of probability),简称几何概型.
则上题中(1)、(2)“甲获胜”的概率分别为1/2,3/5
Y>x
y
x
解 以横坐标X表示报纸送到时间,以纵坐标Y表示父亲离家时间建立平面直角坐标系,假设随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.根据题意,只要点落到阴影部分,就表示父亲在离开家前能
得到报纸(y>x),即时间A发生,所以
两种方法得到的结果相同吗?
对于复杂的实际问题,解题的关键是要建立概率模型,找出随机事件与所有基本事件相对应的几何区域,把问题转化为几何问题,利用几何模型概率公式求解
2.某人午觉醒来,发现表停了,他打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率.
1.两人相约于 7 时到 8 时在公园见面,先到者等候 20 分钟就可离去,求两人能够见面的概率。
几何概型的特点
试验中所有可能出现的结果(基本事件)有无限多个;
每个基本事件出现的可能性相等
古典概型与几何概型的区别
相同:两者基本事件发生的可能性都是相等的;
不同:古典概型要求基本事件有有限个,几何概型要求基本事件有无限多个。
解. 以 7 点为坐标原点,
小时为单位。x,y 分别表示
两人到达的时间,( x,y )
构成边长为 60的正方形S,
显然这是一个几何概率问题。
60
60
o
x
y
S
20
20
他们能见面应满足 | x – y | ≤ 20 ,因此,
A
x – y = – 20
x – y = 20
p = ————— = 1 – —— = 5/9 。
A 的面积
S 的面积
4
9
弄清π是无理数这件事可能是根本没有实际用处的 但是如果我们能弄清楚 那么肯定就不能容忍不去设法把它弄清楚——E·C·Titchmarsh
它们从不同的方式计算着π的值,
1.实验时期:过实验对 π 值进行估算
2.几何法时期:割圆术
3.分析法时期 :
4.计算机时期 :
其中比较有名的就是利用随机试验来估计π的值.
Buffoon,Georges Louis
蒲丰
(1707─1788)
利用蒙特卡罗(Monte Carlo)法进行计算机模拟.
蒲丰投针试验
例3 1777年,法国科学家蒲丰(Buffon)提出了投针
试验问题.平面上画有等距离为a(a>0)的一些平行直
线,现向此平面任意投掷一根长为b( b针与某一平行直线相交的概率.
解
由投掷的任意性可知,
这是一个几何概型问题.
投针可能事件与相交事件:
蒲丰投针试验的应用及意义
历史上一些学者的计算结果(直线距离a=1)
3.1795
859
2520
0.5419
1925
Reina
3.1415929
1808
3408
0.83
1901
Lazzerini
3.1595
489
1030
0.75
1884
Fox
3.137
382
600
1.0
1860
De Morgan
3.1554
1218
3204
0.6
1855
Smith
3.1596
2532
5000
0.8
1850
Wolf
相交次数
投掷次数
针长
时间
试验者
课本例三和例4提供了两种计算面积的方法,请大家参考后,解决下列问题:
3.一个路口的红绿灯,红灯的时间为30秒,黄灯的时间为5秒,绿灯的时间为40秒。当你到达路口时,看见下列三种情况的 概率各是多少?
(1)红灯;(2)黄灯;(3)不是红灯。
4.假设车站每隔 10 分钟发一班车,随机到达车站,问等车时间不超过 3 分钟的概率 ?
5.国家安全机关监听录音机记录了两个间谍的谈话,发现长30min的磁带上,从开始30s处起,有10s长的一段内容包含间谍犯罪的信息.后来发现,这段谈话的部分被某工作人员擦掉了,该工作人员声称他完全是无意中按错了键,使从此后起往后的所有内容都被擦掉了.那么由于按错了键使含有犯罪内容的谈话被部分或全部擦掉的概率有多大?
6.山姆的意大利馅饼屋中设有一个投镖靶 该靶为正方形板.边长为18厘米,挂于前门附近的墙上,顾客花两角伍分的硬币便可投一镖并可有机会赢得一种意大利馅饼中的一个,投镖靶中画有三个同心圆,圆心在靶的中心,当投镖击中半径为1厘米的最内层圆域时.可得到一个大馅饼;当击中半径为1厘米到2厘米之间的环域时,可得到一个中馅饼;如果击中半径为2厘米到3厘米之间的环域时,可得到一个小馅饼,如果击中靶上的其他部分,则得不到馅饼,我们假设每一个顾客都能投镖中靶,并假设每个圆的周边线没有宽度,即每个投镖不会击中线上,试求一顾客将嬴得: (a)一张大馅饼, (b)一张中馅饼, (c)一张小馅饼, (d)没得到馅饼的概率
7.两艘船都要停靠同一泊位,它们可能在一昼夜的任何时刻到达,甲乙两船停靠泊位的时间分别为4小时和2小时,求有一艘船停靠泊位时间必须等待一段时间的概率
对,在几何概型中,如果随机事件所在区域是一个单点,由于单点的长度、面积、体积为0,则它出现的概率为0,但它不是不可能事件;如果一个随机事件所在区域是全部区域扣除一个单点,则它出现的概率为1,但它不是必然事件
思考:“必然事件的概率为1,但概率为1的事件不一定是必然事件。”这种说法对吗?为什么
例如某人7:00~8:00上班,求它刚好不在7:30上班的概率,很明显是一个几何概型,其概率为1,但他7:30上班的确有可能,这就不是必然事件了
7:00 7:30 8:00
几何概型
特点
概率计算公式
均匀随机数
随机模拟方法
