鲁教版(五四制)数学六年级上册 第三章 整式及其加减 复习 课件(共60张)
文档属性
| 名称 | 鲁教版(五四制)数学六年级上册 第三章 整式及其加减 复习 课件(共60张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 18:04:50 | ||
图片预览








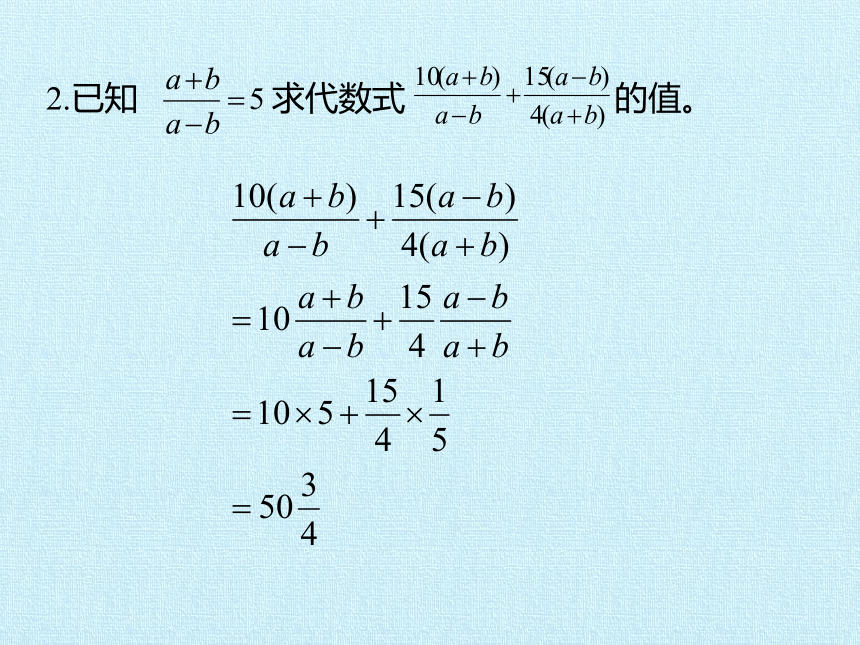


文档简介
(共60张PPT)
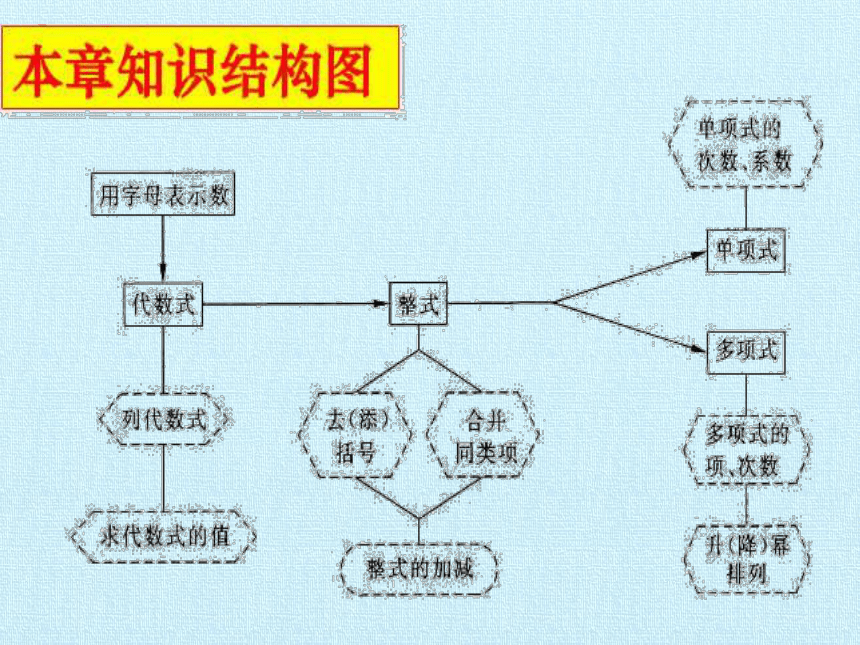
第三章 整式及其加减
复习课件
用字母表示数
1.长方形的周长是2a,宽为b,则它的面积为__________
b(a-b)
2. 将n减少5,再扩大4倍,最后结果为__________
4(n-5)
3.如果m是整数,那么与m相邻的两个整数的和为___________
(m-1)+(m+1)
7.一根绳子原长为1米,从第一天起每天折断它的一半。推断第一天剩余的长度_____,第二天剩余的长度_____…第n天剩余的长度_____
米
米
米
4.用字母n表示偶数为________奇数为___________
5. a与b的差的平方的 是______
6. a的立方与b的立方的和的2倍是______
2n
2n+1
1._____________________________________ 叫做代数式。
用运算符号把数字与字母连接起来的式子
2. 运算符号包括_________________
加,减,乘,除,乘方
判断哪些是代数式
代数式的定义
注意: 单独一个数或一个字母也是代数式。
数字与数字相乘不能省乘号。例如:3×4
一、书写含乘法运算的代数式
1.乘号省,要酌情
2.数相乘,不能省
3.数在前,字母后
4.带分数,要化假
(a+b)×(m+n)=(a+b)(m+n)
t×3常写作3t
(2a+b)×3常写作3(2a+b)
a×
=
a
除号变,分数线
当代数式中出现含有字母的除法运算时,结果一般不用“÷”,而应改用分数线,其中被除数作分子,除数作分母
如ah ÷7=
二、书写含除法运算的代数式
三、书写带有单位名称的代数式
1.遇和差,括号加
如(3a-2b)千克不能写作3a-2b千克;
(t-2) ℃ 不能写作t -2 ℃。
2.是积商,直接放
若代数式是积或商的形式,无需加括号,直接在代数式后写上单位名称即可。
如(1+a%)a米,mn元。
1、直接代入求值
例1:当x=-2,y=-3时,求代数式 的值。
解:当x=-2,y=-3时,
2.整体代入求值
1.
解:
2.
2.已知 求代数式 的值。
输入x
解:如输入x=3,则应先列式为
再列式为
所以表格中应填65
3.转换机:直接输入求值
定义:
单项式中的_________。
次数:
1.当单项式的系数是1或-1时,“1”通常省略不写。
单项式:
系数:
数字或字母的乘积
由_________________组成的式子。
单独的______或________也是单项式。
单项式中的__________________。
数字因数
所有字母的指数和
一个数
一个字母
注意的问题:
2.当式子分母中出现字母时不是单项式。
3.圆周率π是常数,不要看成字母。
4.当单项式的系数是带分数时,通常写成假分数。
5.单项式的系数应包括它前面的性质符号。
6.单项式次数是指所有字母的次数的和,与数字的次数没有关系。
7.单独的数字不含字母, 规定它的次数是零次。
定义:几个__________。
常数项:多项式中_______________。
多项式的次数_________________________
项: 组成多项式中的_____________。
有几项,就叫做_________。
1.在确定多项式的项时,要连同它前面的符号。
2.一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式。
3.在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念。
多项式
单项式的和
每一个单项式
几项式
不含字母的项
多项式中次数最高的项的次数。
注意的问题:
3. 的项是( ),次数是( ),
的项是( ),次数是( ),是( )次( )项式。
2. 的系数是( ),次数是( ), 的系数是
( ),次数是( );
1.在式子:
中,哪些是单项式,哪些是多项式?哪些是整式?
y2
、1-x-5xy2
、-x
练 一练:
y2
1-x-5xy2
2
1、-x、-5xy2
同类项的定义:
(两相同)
合并同类项概念:
_____________________________。
合并同类项法则:
2._________________不变。
2.____________________相同。
1.____相同,
字母
相同的字母的指数也
1.______相加减;
字母和字母的指数
系数
同类项
注意:几个常数项也是______
同类项。
(两无关)
2.与__________无关。
1.与____无关
系数
字母的位置
把多项式中的同类项合并成一项
3.若5x2 y与是 x m yn同类项,则m=( ) n=( )
若5x2 y与 x m yn同的和是单项式, m=( ) n=( )
1.下列各组是不是同类项:
练一练:
(1) 4abc 与 4ab
(2) -5 m2 n3 与 2n3 m2
(3) -0.3 x2 y 与 y x2
2.合并下列同类项:
(1) 3xy – 4 xy – xy = ( )
(2) -a-a-2a=( )
不是
是
是
–2xy
–4a
2
1
2
1
2.若 与 是同类项,则m+n=___
4.若 ,则m+n-p=______
5
4
3.若 与 的和是一个单项式,则 =___
-4
1.下列各式中,是同类项的是:___________
① 与
② 与
③ 与
⑤ 与
⑥-125与
③⑤⑥
④ 与
整式的加减混合运算步骤(有括号先去括号)
1.找同类项,做好标记。
2.利用加法的交换律和结合律把同类项放在一起。
3.利用乘法分配律计算结果。
4.按要求按“升”或“降”幂排列。
找
般
并
排
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
“去括号,看符号。是‘+’号,不变号,是‘-’号,全变号”
一:去括号
二:计算
(按照先小括号,再中括号,最后大括号的顺序)
3.多项式 __________与__________的和是__________,它们的差
是__________,多项式__________减去一个多项后是__________,则这个多项式是 __________
1.去括号: (1) +(x-3)= (2) -(x-3)=
(3)-(x+5y-2)= (4)+(3x-5y+6z)=
练一练:
x-3
-x+3
- x- 5y+2
3x-5y+6z
2.计算:(1)x-(-y -z+1)= ______
( 2 ) m+(-n+q)=__________;
( 3 ) a - ( b+c-3)=__________;
( 4 ) x+(5-3y)= __________
x-5xy2
-3x+xy2
-5a+4ab3
2a
x+y +z -1
m-n+q
a-b-c+3
x+5-3y
-2x-4xy2
4x-6xy2
-7a+4ab3
4.化简
已知
,
求
解:
跟踪练习:
已知
求
2. 已知
1.
求:
(1)
(2)
例:两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50千米/时,水流速度是a千米/时。
(1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
解:顺水航速=船速+水速=50+a(千米/时)
顺水航速=船速-水速=50-a(千米/时)
(2)2小时后甲船比乙船多航行
2(50+a)-2(50-a)
=100+2a-100+2a
=4a(千米)
(1) 2小时后两船相距
2(50+a)+2(50-a)
=100+2a+100-2a
=200(千米)
跟踪练习:
飞机的无风航速为a千米/时,风速为20千米/时,飞机顺风飞行6小时的行程是多少?飞机逆风飞行3小时的行程是多少?两个行程的相差是多少?
一、填空:
1.a的倒数与b的相反数的差,用代数式表示是______。
2.a、b两数的平方差除a、b两数和的平方,所得商为_______。
3.一个两位数,个位上数字是x,十位上数字是个位数字的两倍,这个两位数是_______。
4.若3x 2m-1 y2与-2xy n-1是同类项,则2m-n= _______。
5.若x+y=6,则2- x-y的值是_______。
6.甲、乙两辆车同时从A、B两地相向而行,甲车速度为v千米/时,乙车速度是甲车的2倍还多2千米,若两车出发后4小时相遇,则A、B两地路程可以表示成_______ ;若v=40,则A、B两地路程是_____ 千米。
巩固练习
二、列代数式:
1、已知长方形的宽为(2a-b)cm,长比宽多(a-b)cm,求这个长方形的周长。
3a2b - [2a2b -(2abc - a2c)- 4a2c ] – abc
四、求代数式
3a2b - [2a2b -(2abc - a2c)- 4a2c ] – abc的值,
其中a=-2,b=-3,c=1
三、化简:
1.观察一列数:3,8,13,18,23,28,……,
依次规律,在数列中第2004个数是_____。
2.下面一组按规律排列的数:2,4,8,16,
……,第2005个数应是_______。
10018
22005
探究
3.按规律填数:
(1)2,7,12,17,( ),( ),……
(2)1,2,4,8,16,( ),( ),……
22
27
32
64
4.观察下列算式:
(1)第5个等式是___________________;
(2)第n个等式是________________________________
-
=
4=1×4
-
=12=3×4
-
=20=5×4
-
=28=7×4
按规律回答:
-
=36=9×4
-
=(2n-1) ×4
5.如图,在2005年3月的日历上:
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
任意圈出一竖
列上相邻的三个
数,设中间的一个
数为x,则其余两
个数分别为
.
x-7,x+7
用火柴棒按下图的方式搭三角形 。
③
②
①
练一练
三角形个数 1 2 3 4 5
火柴棒根数
⑴填写下表 :
⑵照这样的规律搭下去,搭n个 这样的三角形需要多少根火柴棒?
4n+1
5
9
13
17
21
①
②
③
④
做一做:
用棋子摆出下列一组图形:
⑴摆第1个图形用_____枚棋子,摆第2个图形用_____枚棋子,摆第3个图形用______枚棋子;
⑵按照这种方式摆下去,摆第n个图形用_____枚棋子,摆第100个图形用_______枚棋子。
3
6
9
3n
300
1.探索规律并填空:
(1) .....
。
思考:
(2)计算: .
1.求当x= 时,多项式
的值。
解:原式=
=
=
把x= 带入 中,得
∴ 原式=5
补充例题:
a
0
b
2.已知数a,b在数轴上的位置如图所示
化简下列式子:
∴原式=-a-2[-(a+b)]-3(b-a)
解:由题意知:a<0,b>0且|a|>|b|
=-a+2[a+b]-3b+3a
=-a+2a+2b-3b+3a
=(-a+2a+3a)+(2b-3b)
=4a-b
3.当x=1时, 则当x=-1时,
解:将x=1代入 中得:
a+b-2=3
∴ a+b=5;
当x=-1时
=-a-b-2
=-(a+b)-2
=-7
=-5-2
4.已知多项式A= ,B= ,C=
求 2A-5B+3C=
解:原式=
=
=
=
5.如果关于x的多项式 的值与x
无关,则a的取值为_____。
解:原式=
由题意知,则:
6a-6=0
∴a=1
1
6.如果关于x,y的多项式 的差
不含有二次项,求 的值。
解:原式=
由题意知,则:
m-3=0
2+2n=0
∴m=3,n=-1;
∴ = = -1
一、概念中的易错题
二、运算中的易错题
易错点总结:
1.单项式的定义
例1.下列各式子中,是单项式的有______________(填序号)
①、②、④、⑦
注意:1.单个的字母或数字也是单项式;
2.用加减号把数字或字母连接在一起
的式子不是单项式;
3.只用乘号把数字或字母连接在一起
的式子仍是单项式;
4.当式子中出现分母时,要留意分母里有
没有字母,有字母的就不是单项式,如
果分母没有字母的仍有可能是单项式
(注:“π”当作数字,而不是字母)
2.单项式的系数与次数
单项式
系数
次数
例2 指出下列单项式的系数和次数;
注意:1.字母的系数“1” 可以省略的,但不代表没有系
数(次数也是同样道理);
2.有分母的单项式,分母中的数字也是单项式系
数的一部分;
3.注意“π”不是字母,而是数字,属于系数的一
部分;
4.计算次数的时候并不是简单的见到指数就相
加,注意单项式的次数指的是字母的指数和;
3.多项式的项数与次数
例3 下列多项式次数为3的是( )
C
例4 请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项;
注意(1)多项式的次数不是所有项的次数的和,而是它的最高
次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次, “π”当作数字,而不是字母。
4.书写格式中的易错点
例5 下列各个式子中,书写格式正确的是( )
1.代数式中用到乘法时,若是数字与数字乘,要用“×”
若是数字与字母乘,乘号通常写成”.”或省略不写,如
3×y应写成3·y或3y,且数字与字母相乘时,字母与
字母相乘,乘号通常写成“·”或省略不写。
2.带分数与字母相乘,要写成假分数
3.代数式中出现除法运算时,一般用分数写,即用分数
线代替除号。
4.系数一般写在字母的前面,且系数“1”往往会省略;
F
例6 王强班上有男生m人,女生比男生的一半多5人,王强班上的总人数(用m表示)为______人。
易错点:结果不进行化简,直接写
点拨:结果中有 它们是同类项,应合并以保证最后的结果最简。正确的写法是
二、运算过程中的易错题
1.同类项的判定与合并同类项的法则:
例1 判断下列各式是否是同类项?
点拨:对于(1)、(3),考察的是同类项的定义,所含字母相同,相同字母的指数也相同的称为同类项;所以(1)、(3)不是同类项;
对于(2),虽然好像它们的次数不一样,但其实它们都是常数项,所以,它们都是同类项;
对于(4),虽然它们的系数不同,字母的顺序也不同,但它依然满足同类项的定义,是同类项;
答:(2)、(4)是同类项,(1)(3)不是同类项;
例2 下列合并同类项的结果错误的有_______________.
①、②、③、④、⑤
注意:
1.合并同类项的法则是把同类项的系数相加,字母和字母的次数不变;
2.合并同类项后也要注意书写格式;
3.如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;
0
例3 合并同类项:
小明的解法:
(1)错在把所有项都当作同类项了;
正确的解法:
例3 合并同类项:
小明的解法:
(2)错在把结合同类项时弄错了符号;
正确的解法:
总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的。
2.去括号中的易错题:
判断下列各式是否正确:
√
×
×
( )
( )
( )
×
( )
去括号时,
1.注意括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2.注意外面有系数的,各项都要乘以那个系数;
练一练:
化简下列各式:
整式的加减一般步骤是(1)如果有括号就先去括号,
(2)然后再合并同类项。
3.化简求值中的易错题:
(先去括号)
(降幂排列)
(合并同类项,化简完成)
当x=-2时
(代入)
(代入时注意添上括号,乘号改回“×”)
;
2
)
6
4
3
(
3
1
)
1
4
(
3
2
3
2
-
=
+
+
-
+
-
x
x
x
x
x
的值,其中
求多项式
4.多重括号化简的易错题
注意:有多重括号的,一般先去小括号,再去中括号,最后再去大括号;
]
2
)
1
(
3
2
[
3
2
2
2
x
x
x
x
+
-
-
-
1.去掉下列各式中的括号。
(1)8m-(3n+5)
(2)n-4(3-2m)
(3)2(a-2b)-3(2m-n)
=8m-3n-5
=n-12+8m
=2a-4b-6m+3n
2.化简:
-(3x-2y+z)-[5x-x+2y-z-3x]
解:原式=
-(3x-2y+z)-[5x-(x-2y+z)-3x]
=-(3x-2y+z)-[x+2y-z]
=-(3x-2y+z)-[(5x-x-3x)+2y-z]
=-3x+2y-z-x-2y+z
=(-3x-x)+(2y-2y)+(-z+z)
=-4x
练一练:
5.“A+2B”类型的易错题:
例1 若多项式 计算多项式A-2B;
注意:列式时要先加上括号,再去括号;
例2 一个多项式A加上 得 ,求这个多项式A?
注意:我们在移项的时候是整体移项,不要漏了添上括号;
6.实际问题中的易错题:
例1 某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在再次下调20%,使收费标准为n元/分钟,那么原收费标准为 ( )
B
点拨:为了弄清各数之间的关系,我们可以借助方程来求解.假设原收费标准为每分钟x元,可得:
解得 .应选B.
例2 若长方形的一边长为a+2b,另一边长比它的3倍少a-b,求这个长方形的周长?
分析:如果直接列式的话,非常麻烦,我们可以先求出另一边长,再求周长,这样就比较容易求出答案;
解:一边长为:a+2b;
另一边长为:3(a+2b)-(a-b)
=3a+6b-a+b
=3a-a+6b+b
=2a+7b;
周长为:2(a+2b+2a+7b)
=2(a+2a+2b+7b)
=2(3a+9b)
=6a+18b;
答:长方形的周长为6a+18b
计算与求值:
作业:
实际问题
(1)小明在实践课中做一个长方形模型,一边为3a+2b,另一边比它小a-b,则长方形的周长为多少?
(2)大众超市出售一种商品其原价为a元,现三种调价方案:1.先提价格上涨20%,再降价格20%
2. 先降价格上涨20%,再提价格20%
3. 先提价格上涨15%,再降价格15%
问用这三种方案调价结果是否一样?最后是不是都恢复了原价
谢 谢
第三章 整式及其加减
复习课件
用字母表示数
1.长方形的周长是2a,宽为b,则它的面积为__________
b(a-b)
2. 将n减少5,再扩大4倍,最后结果为__________
4(n-5)
3.如果m是整数,那么与m相邻的两个整数的和为___________
(m-1)+(m+1)
7.一根绳子原长为1米,从第一天起每天折断它的一半。推断第一天剩余的长度_____,第二天剩余的长度_____…第n天剩余的长度_____
米
米
米
4.用字母n表示偶数为________奇数为___________
5. a与b的差的平方的 是______
6. a的立方与b的立方的和的2倍是______
2n
2n+1
1._____________________________________ 叫做代数式。
用运算符号把数字与字母连接起来的式子
2. 运算符号包括_________________
加,减,乘,除,乘方
判断哪些是代数式
代数式的定义
注意: 单独一个数或一个字母也是代数式。
数字与数字相乘不能省乘号。例如:3×4
一、书写含乘法运算的代数式
1.乘号省,要酌情
2.数相乘,不能省
3.数在前,字母后
4.带分数,要化假
(a+b)×(m+n)=(a+b)(m+n)
t×3常写作3t
(2a+b)×3常写作3(2a+b)
a×
=
a
除号变,分数线
当代数式中出现含有字母的除法运算时,结果一般不用“÷”,而应改用分数线,其中被除数作分子,除数作分母
如ah ÷7=
二、书写含除法运算的代数式
三、书写带有单位名称的代数式
1.遇和差,括号加
如(3a-2b)千克不能写作3a-2b千克;
(t-2) ℃ 不能写作t -2 ℃。
2.是积商,直接放
若代数式是积或商的形式,无需加括号,直接在代数式后写上单位名称即可。
如(1+a%)a米,mn元。
1、直接代入求值
例1:当x=-2,y=-3时,求代数式 的值。
解:当x=-2,y=-3时,
2.整体代入求值
1.
解:
2.
2.已知 求代数式 的值。
输入x
解:如输入x=3,则应先列式为
再列式为
所以表格中应填65
3.转换机:直接输入求值
定义:
单项式中的_________。
次数:
1.当单项式的系数是1或-1时,“1”通常省略不写。
单项式:
系数:
数字或字母的乘积
由_________________组成的式子。
单独的______或________也是单项式。
单项式中的__________________。
数字因数
所有字母的指数和
一个数
一个字母
注意的问题:
2.当式子分母中出现字母时不是单项式。
3.圆周率π是常数,不要看成字母。
4.当单项式的系数是带分数时,通常写成假分数。
5.单项式的系数应包括它前面的性质符号。
6.单项式次数是指所有字母的次数的和,与数字的次数没有关系。
7.单独的数字不含字母, 规定它的次数是零次。
定义:几个__________。
常数项:多项式中_______________。
多项式的次数_________________________
项: 组成多项式中的_____________。
有几项,就叫做_________。
1.在确定多项式的项时,要连同它前面的符号。
2.一个多项式的次数最高项的次数是几,就说这个多项式是几次多项式。
3.在多项式中,每个单项式都是这个多项式的项,每一项都有系数,但对整个多项式来说,没有系数的概念,只有次数的概念。
多项式
单项式的和
每一个单项式
几项式
不含字母的项
多项式中次数最高的项的次数。
注意的问题:
3. 的项是( ),次数是( ),
的项是( ),次数是( ),是( )次( )项式。
2. 的系数是( ),次数是( ), 的系数是
( ),次数是( );
1.在式子:
中,哪些是单项式,哪些是多项式?哪些是整式?
y2
、1-x-5xy2
、-x
练 一练:
y2
1-x-5xy2
2
1、-x、-5xy2
同类项的定义:
(两相同)
合并同类项概念:
_____________________________。
合并同类项法则:
2._________________不变。
2.____________________相同。
1.____相同,
字母
相同的字母的指数也
1.______相加减;
字母和字母的指数
系数
同类项
注意:几个常数项也是______
同类项。
(两无关)
2.与__________无关。
1.与____无关
系数
字母的位置
把多项式中的同类项合并成一项
3.若5x2 y与是 x m yn同类项,则m=( ) n=( )
若5x2 y与 x m yn同的和是单项式, m=( ) n=( )
1.下列各组是不是同类项:
练一练:
(1) 4abc 与 4ab
(2) -5 m2 n3 与 2n3 m2
(3) -0.3 x2 y 与 y x2
2.合并下列同类项:
(1) 3xy – 4 xy – xy = ( )
(2) -a-a-2a=( )
不是
是
是
–2xy
–4a
2
1
2
1
2.若 与 是同类项,则m+n=___
4.若 ,则m+n-p=______
5
4
3.若 与 的和是一个单项式,则 =___
-4
1.下列各式中,是同类项的是:___________
① 与
② 与
③ 与
⑤ 与
⑥-125与
③⑤⑥
④ 与
整式的加减混合运算步骤(有括号先去括号)
1.找同类项,做好标记。
2.利用加法的交换律和结合律把同类项放在一起。
3.利用乘法分配律计算结果。
4.按要求按“升”或“降”幂排列。
找
般
并
排
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同。
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反。
“去括号,看符号。是‘+’号,不变号,是‘-’号,全变号”
一:去括号
二:计算
(按照先小括号,再中括号,最后大括号的顺序)
3.多项式 __________与__________的和是__________,它们的差
是__________,多项式__________减去一个多项后是__________,则这个多项式是 __________
1.去括号: (1) +(x-3)= (2) -(x-3)=
(3)-(x+5y-2)= (4)+(3x-5y+6z)=
练一练:
x-3
-x+3
- x- 5y+2
3x-5y+6z
2.计算:(1)x-(-y -z+1)= ______
( 2 ) m+(-n+q)=__________;
( 3 ) a - ( b+c-3)=__________;
( 4 ) x+(5-3y)= __________
x-5xy2
-3x+xy2
-5a+4ab3
2a
x+y +z -1
m-n+q
a-b-c+3
x+5-3y
-2x-4xy2
4x-6xy2
-7a+4ab3
4.化简
已知
,
求
解:
跟踪练习:
已知
求
2. 已知
1.
求:
(1)
(2)
例:两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50千米/时,水流速度是a千米/时。
(1)2小时后两船相距多远?
(2)2小时后甲船比乙船多航行多少千米?
解:顺水航速=船速+水速=50+a(千米/时)
顺水航速=船速-水速=50-a(千米/时)
(2)2小时后甲船比乙船多航行
2(50+a)-2(50-a)
=100+2a-100+2a
=4a(千米)
(1) 2小时后两船相距
2(50+a)+2(50-a)
=100+2a+100-2a
=200(千米)
跟踪练习:
飞机的无风航速为a千米/时,风速为20千米/时,飞机顺风飞行6小时的行程是多少?飞机逆风飞行3小时的行程是多少?两个行程的相差是多少?
一、填空:
1.a的倒数与b的相反数的差,用代数式表示是______。
2.a、b两数的平方差除a、b两数和的平方,所得商为_______。
3.一个两位数,个位上数字是x,十位上数字是个位数字的两倍,这个两位数是_______。
4.若3x 2m-1 y2与-2xy n-1是同类项,则2m-n= _______。
5.若x+y=6,则2- x-y的值是_______。
6.甲、乙两辆车同时从A、B两地相向而行,甲车速度为v千米/时,乙车速度是甲车的2倍还多2千米,若两车出发后4小时相遇,则A、B两地路程可以表示成_______ ;若v=40,则A、B两地路程是_____ 千米。
巩固练习
二、列代数式:
1、已知长方形的宽为(2a-b)cm,长比宽多(a-b)cm,求这个长方形的周长。
3a2b - [2a2b -(2abc - a2c)- 4a2c ] – abc
四、求代数式
3a2b - [2a2b -(2abc - a2c)- 4a2c ] – abc的值,
其中a=-2,b=-3,c=1
三、化简:
1.观察一列数:3,8,13,18,23,28,……,
依次规律,在数列中第2004个数是_____。
2.下面一组按规律排列的数:2,4,8,16,
……,第2005个数应是_______。
10018
22005
探究
3.按规律填数:
(1)2,7,12,17,( ),( ),……
(2)1,2,4,8,16,( ),( ),……
22
27
32
64
4.观察下列算式:
(1)第5个等式是___________________;
(2)第n个等式是________________________________
-
=
4=1×4
-
=12=3×4
-
=20=5×4
-
=28=7×4
按规律回答:
-
=36=9×4
-
=(2n-1) ×4
5.如图,在2005年3月的日历上:
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
任意圈出一竖
列上相邻的三个
数,设中间的一个
数为x,则其余两
个数分别为
.
x-7,x+7
用火柴棒按下图的方式搭三角形 。
③
②
①
练一练
三角形个数 1 2 3 4 5
火柴棒根数
⑴填写下表 :
⑵照这样的规律搭下去,搭n个 这样的三角形需要多少根火柴棒?
4n+1
5
9
13
17
21
①
②
③
④
做一做:
用棋子摆出下列一组图形:
⑴摆第1个图形用_____枚棋子,摆第2个图形用_____枚棋子,摆第3个图形用______枚棋子;
⑵按照这种方式摆下去,摆第n个图形用_____枚棋子,摆第100个图形用_______枚棋子。
3
6
9
3n
300
1.探索规律并填空:
(1) .....
。
思考:
(2)计算: .
1.求当x= 时,多项式
的值。
解:原式=
=
=
把x= 带入 中,得
∴ 原式=5
补充例题:
a
0
b
2.已知数a,b在数轴上的位置如图所示
化简下列式子:
∴原式=-a-2[-(a+b)]-3(b-a)
解:由题意知:a<0,b>0且|a|>|b|
=-a+2[a+b]-3b+3a
=-a+2a+2b-3b+3a
=(-a+2a+3a)+(2b-3b)
=4a-b
3.当x=1时, 则当x=-1时,
解:将x=1代入 中得:
a+b-2=3
∴ a+b=5;
当x=-1时
=-a-b-2
=-(a+b)-2
=-7
=-5-2
4.已知多项式A= ,B= ,C=
求 2A-5B+3C=
解:原式=
=
=
=
5.如果关于x的多项式 的值与x
无关,则a的取值为_____。
解:原式=
由题意知,则:
6a-6=0
∴a=1
1
6.如果关于x,y的多项式 的差
不含有二次项,求 的值。
解:原式=
由题意知,则:
m-3=0
2+2n=0
∴m=3,n=-1;
∴ = = -1
一、概念中的易错题
二、运算中的易错题
易错点总结:
1.单项式的定义
例1.下列各式子中,是单项式的有______________(填序号)
①、②、④、⑦
注意:1.单个的字母或数字也是单项式;
2.用加减号把数字或字母连接在一起
的式子不是单项式;
3.只用乘号把数字或字母连接在一起
的式子仍是单项式;
4.当式子中出现分母时,要留意分母里有
没有字母,有字母的就不是单项式,如
果分母没有字母的仍有可能是单项式
(注:“π”当作数字,而不是字母)
2.单项式的系数与次数
单项式
系数
次数
例2 指出下列单项式的系数和次数;
注意:1.字母的系数“1” 可以省略的,但不代表没有系
数(次数也是同样道理);
2.有分母的单项式,分母中的数字也是单项式系
数的一部分;
3.注意“π”不是字母,而是数字,属于系数的一
部分;
4.计算次数的时候并不是简单的见到指数就相
加,注意单项式的次数指的是字母的指数和;
3.多项式的项数与次数
例3 下列多项式次数为3的是( )
C
例4 请说出下列各多项式是几次几项式,并写出多项式的最高次项和常数项;
注意(1)多项式的次数不是所有项的次数的和,而是它的最高
次项次数;
(2)多项式的每一项都包含它前面的符号;
(3)再强调一次, “π”当作数字,而不是字母。
4.书写格式中的易错点
例5 下列各个式子中,书写格式正确的是( )
1.代数式中用到乘法时,若是数字与数字乘,要用“×”
若是数字与字母乘,乘号通常写成”.”或省略不写,如
3×y应写成3·y或3y,且数字与字母相乘时,字母与
字母相乘,乘号通常写成“·”或省略不写。
2.带分数与字母相乘,要写成假分数
3.代数式中出现除法运算时,一般用分数写,即用分数
线代替除号。
4.系数一般写在字母的前面,且系数“1”往往会省略;
F
例6 王强班上有男生m人,女生比男生的一半多5人,王强班上的总人数(用m表示)为______人。
易错点:结果不进行化简,直接写
点拨:结果中有 它们是同类项,应合并以保证最后的结果最简。正确的写法是
二、运算过程中的易错题
1.同类项的判定与合并同类项的法则:
例1 判断下列各式是否是同类项?
点拨:对于(1)、(3),考察的是同类项的定义,所含字母相同,相同字母的指数也相同的称为同类项;所以(1)、(3)不是同类项;
对于(2),虽然好像它们的次数不一样,但其实它们都是常数项,所以,它们都是同类项;
对于(4),虽然它们的系数不同,字母的顺序也不同,但它依然满足同类项的定义,是同类项;
答:(2)、(4)是同类项,(1)(3)不是同类项;
例2 下列合并同类项的结果错误的有_______________.
①、②、③、④、⑤
注意:
1.合并同类项的法则是把同类项的系数相加,字母和字母的次数不变;
2.合并同类项后也要注意书写格式;
3.如果两个同类项的系数互为相反数,那么合并同类项后,结果得____;
0
例3 合并同类项:
小明的解法:
(1)错在把所有项都当作同类项了;
正确的解法:
例3 合并同类项:
小明的解法:
(2)错在把结合同类项时弄错了符号;
正确的解法:
总之,合并同类项现要找出式子中的同类项,并把它们写在一起,最后合并,注意同类项的系数是带符号的。
2.去括号中的易错题:
判断下列各式是否正确:
√
×
×
( )
( )
( )
×
( )
去括号时,
1.注意括号外面的符号,括号前面是“+”号,把括号和它前面的“+”号去掉,括号里各项都不用变符号;括号前面是“—”号,把括号和它前面的“—”号去掉,括号里各项都改变符号。
2.注意外面有系数的,各项都要乘以那个系数;
练一练:
化简下列各式:
整式的加减一般步骤是(1)如果有括号就先去括号,
(2)然后再合并同类项。
3.化简求值中的易错题:
(先去括号)
(降幂排列)
(合并同类项,化简完成)
当x=-2时
(代入)
(代入时注意添上括号,乘号改回“×”)
;
2
)
6
4
3
(
3
1
)
1
4
(
3
2
3
2
-
=
+
+
-
+
-
x
x
x
x
x
的值,其中
求多项式
4.多重括号化简的易错题
注意:有多重括号的,一般先去小括号,再去中括号,最后再去大括号;
]
2
)
1
(
3
2
[
3
2
2
2
x
x
x
x
+
-
-
-
1.去掉下列各式中的括号。
(1)8m-(3n+5)
(2)n-4(3-2m)
(3)2(a-2b)-3(2m-n)
=8m-3n-5
=n-12+8m
=2a-4b-6m+3n
2.化简:
-(3x-2y+z)-[5x-x+2y-z-3x]
解:原式=
-(3x-2y+z)-[5x-(x-2y+z)-3x]
=-(3x-2y+z)-[x+2y-z]
=-(3x-2y+z)-[(5x-x-3x)+2y-z]
=-3x+2y-z-x-2y+z
=(-3x-x)+(2y-2y)+(-z+z)
=-4x
练一练:
5.“A+2B”类型的易错题:
例1 若多项式 计算多项式A-2B;
注意:列式时要先加上括号,再去括号;
例2 一个多项式A加上 得 ,求这个多项式A?
注意:我们在移项的时候是整体移项,不要漏了添上括号;
6.实际问题中的易错题:
例1 某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在再次下调20%,使收费标准为n元/分钟,那么原收费标准为 ( )
B
点拨:为了弄清各数之间的关系,我们可以借助方程来求解.假设原收费标准为每分钟x元,可得:
解得 .应选B.
例2 若长方形的一边长为a+2b,另一边长比它的3倍少a-b,求这个长方形的周长?
分析:如果直接列式的话,非常麻烦,我们可以先求出另一边长,再求周长,这样就比较容易求出答案;
解:一边长为:a+2b;
另一边长为:3(a+2b)-(a-b)
=3a+6b-a+b
=3a-a+6b+b
=2a+7b;
周长为:2(a+2b+2a+7b)
=2(a+2a+2b+7b)
=2(3a+9b)
=6a+18b;
答:长方形的周长为6a+18b
计算与求值:
作业:
实际问题
(1)小明在实践课中做一个长方形模型,一边为3a+2b,另一边比它小a-b,则长方形的周长为多少?
(2)大众超市出售一种商品其原价为a元,现三种调价方案:1.先提价格上涨20%,再降价格20%
2. 先降价格上涨20%,再提价格20%
3. 先提价格上涨15%,再降价格15%
问用这三种方案调价结果是否一样?最后是不是都恢复了原价
谢 谢
