2021--2022学年人教版七年级数学上册3.3 解一元一次方程(二)去分母 课件 (22张)
文档属性
| 名称 | 2021--2022学年人教版七年级数学上册3.3 解一元一次方程(二)去分母 课件 (22张) |  | |
| 格式 | zip | ||
| 文件大小 | 176.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 08:40:51 | ||
图片预览






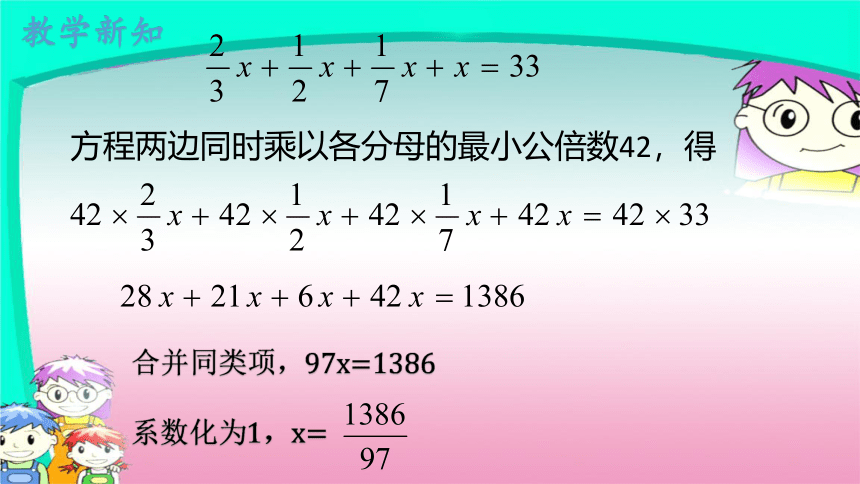


文档简介
(共22张PPT)
3.3 解一元一次方程(二)
第2课时
去分母
学习目标
1.掌握去分母解一元一次方程的方法,并能解这种类型的方程,学会一元一次方程的解法的一般步骤;
2.通过列方程解决实际问题,逐步建立方程的思想,了解数学中的化归思想。
情境1:英国伦敦博物馆里保留着一部极其珍贵的文物---纸草书。这是古代该既然用象形文字在一种用纸莎草压制成的草片上的著作。它于公元前1700年左右写成。这部书中记载了许多有关数学的问题,其中有一道著名的求未知数的问题。
情境导入
问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,这个数是多少?
情境导入
应该如何求这个数?
设这个数是x,
列方程
当时的埃及人如果把问题写成这种形式,他一定是最早的方程。
问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,这个数是多少?
这个方程与之前学习的方程有什么不一样?怎么解这个方程?
你认为采取什么方法比较简便?
两边都乘以42,去掉分母的方法比较简单。
这节课就一起来研究一下如何去分母来解一元一次方程
教学新知
一. 去分母解一元一次方程
我们怎样去分母呢
方程两边同时乘以42.
乘以的42是从哪里来的?
42是所有分母的最小公倍数
去分母的依据是什么?
依据等式 的性质
教学新知
方程两边同时乘以各分母的最小公倍数42,得
合并同类项,97x=1386
系数化为1,x=
教学新知
为了更全面的讨论问题,我们再以方程
为例,看看解有分数系数的一元一次方程的步骤。
教学新知
去分母(方程两边同时乘以各分母的最小公倍数)
移项得,15x-3x+4x=20-5+6-2
合并同类项得,16x=7
系数化为1 得,x=
5(3x+1)-10×2=(3x-2)-2(2x+3)
去括号得,15x+5-20=3x-2-4x+6
注意:方程左边的-2也要乘10,不要漏乘
教学新知
1. 去分母(方程两边同时乘以各分母的最小公倍数)
3. 移项
4. 合并同类项
5. 系数化为1
根据上面两道题的解题流程,思考一下,解含分数系的一元一次方程的步骤有哪些?
2. 去括号
教学新知
主要依据是等式的基本性质和运算律等。
通过这些步骤可以使以x为未知数的方程逐步向着x=a的形式转化,这个过程的主要依据是什么?
教学新知
二. 例题讲解
例1:解下列方程
(1)
去括号得,2x+2-4=8+2-x
移项得,2x+x=8+2+4-2
合并同类项得,3x=12
系数化为1 得,x=4
去分母得,2(x+1)-4 = 8 + (2 - x )
教学新知
二. 例题讲解
例1:解下列方程
(2)
去分母得,18x+3(x-1)=18-2(2x-1 )
移项得,18x+3x+4x=18+2+3
合并同类项得,25x=23
系数化为1 得,x=
去括号得,18x+3x-3=18-4x+2
教学新知
变式:
这个方程该如何解呢?和我们前面做的几个去分母的方程有什么不同之处呢?
之前的方程分母都是整数,现在的分母是小数
怎样把分母由小数化成整数呢?
根据分数的基本性质,把含小数的项的分子,分母乘一个适当的数,把小数化成整数。
教学新知
教学新知
去分母得,4(50x+200)-12x =3(3x+12 )-131
移项得,200x-9x-12x=36-131-800
合并同类项得,179x=-895
系数化为1 得,x= -5
去括号得,200x+800-12x=9x+36-131
巩固练习
1.若代数式4X-5与 的值相等,则x的值是( )
A B C D
A
2.方程 的解是( )
A 6
B -6
C 7
D -7
D
3.方程 去分母正确的是( )
A 3x-2(2x-1)=6
B 3x-2(2x-1)=1
C 3x-4x-1=6
D x-(2x-1)=1
A
4.解方程
(1)
(2)
(3)
(4)
总结提升
1.本节课你学到了哪些知识?
2.去分母的依据是什么?去分母的作用是什么?
3.去分母时,方程两边所乘的数如何确定?
谢谢观看!
3.3 解一元一次方程(二)
第2课时
去分母
学习目标
1.掌握去分母解一元一次方程的方法,并能解这种类型的方程,学会一元一次方程的解法的一般步骤;
2.通过列方程解决实际问题,逐步建立方程的思想,了解数学中的化归思想。
情境1:英国伦敦博物馆里保留着一部极其珍贵的文物---纸草书。这是古代该既然用象形文字在一种用纸莎草压制成的草片上的著作。它于公元前1700年左右写成。这部书中记载了许多有关数学的问题,其中有一道著名的求未知数的问题。
情境导入
问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,这个数是多少?
情境导入
应该如何求这个数?
设这个数是x,
列方程
当时的埃及人如果把问题写成这种形式,他一定是最早的方程。
问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,这个数是多少?
这个方程与之前学习的方程有什么不一样?怎么解这个方程?
你认为采取什么方法比较简便?
两边都乘以42,去掉分母的方法比较简单。
这节课就一起来研究一下如何去分母来解一元一次方程
教学新知
一. 去分母解一元一次方程
我们怎样去分母呢
方程两边同时乘以42.
乘以的42是从哪里来的?
42是所有分母的最小公倍数
去分母的依据是什么?
依据等式 的性质
教学新知
方程两边同时乘以各分母的最小公倍数42,得
合并同类项,97x=1386
系数化为1,x=
教学新知
为了更全面的讨论问题,我们再以方程
为例,看看解有分数系数的一元一次方程的步骤。
教学新知
去分母(方程两边同时乘以各分母的最小公倍数)
移项得,15x-3x+4x=20-5+6-2
合并同类项得,16x=7
系数化为1 得,x=
5(3x+1)-10×2=(3x-2)-2(2x+3)
去括号得,15x+5-20=3x-2-4x+6
注意:方程左边的-2也要乘10,不要漏乘
教学新知
1. 去分母(方程两边同时乘以各分母的最小公倍数)
3. 移项
4. 合并同类项
5. 系数化为1
根据上面两道题的解题流程,思考一下,解含分数系的一元一次方程的步骤有哪些?
2. 去括号
教学新知
主要依据是等式的基本性质和运算律等。
通过这些步骤可以使以x为未知数的方程逐步向着x=a的形式转化,这个过程的主要依据是什么?
教学新知
二. 例题讲解
例1:解下列方程
(1)
去括号得,2x+2-4=8+2-x
移项得,2x+x=8+2+4-2
合并同类项得,3x=12
系数化为1 得,x=4
去分母得,2(x+1)-4 = 8 + (2 - x )
教学新知
二. 例题讲解
例1:解下列方程
(2)
去分母得,18x+3(x-1)=18-2(2x-1 )
移项得,18x+3x+4x=18+2+3
合并同类项得,25x=23
系数化为1 得,x=
去括号得,18x+3x-3=18-4x+2
教学新知
变式:
这个方程该如何解呢?和我们前面做的几个去分母的方程有什么不同之处呢?
之前的方程分母都是整数,现在的分母是小数
怎样把分母由小数化成整数呢?
根据分数的基本性质,把含小数的项的分子,分母乘一个适当的数,把小数化成整数。
教学新知
教学新知
去分母得,4(50x+200)-12x =3(3x+12 )-131
移项得,200x-9x-12x=36-131-800
合并同类项得,179x=-895
系数化为1 得,x= -5
去括号得,200x+800-12x=9x+36-131
巩固练习
1.若代数式4X-5与 的值相等,则x的值是( )
A B C D
A
2.方程 的解是( )
A 6
B -6
C 7
D -7
D
3.方程 去分母正确的是( )
A 3x-2(2x-1)=6
B 3x-2(2x-1)=1
C 3x-4x-1=6
D x-(2x-1)=1
A
4.解方程
(1)
(2)
(3)
(4)
总结提升
1.本节课你学到了哪些知识?
2.去分母的依据是什么?去分母的作用是什么?
3.去分母时,方程两边所乘的数如何确定?
谢谢观看!
