2021-2022学年人教版八年级数学下册 19.2.2 一次函数的实际应用 第4课时 课件(共17张)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册 19.2.2 一次函数的实际应用 第4课时 课件(共17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 155.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 18:42:51 | ||
图片预览






文档简介
(共17张PPT)
第十九章 一次函数
19.2.2 第4课时 一次函数的实际应用
知识回顾
1.什么是一次函数?确定一个一次函数需要几个因素? 是哪几个?
y=kx+b(k≠0)叫做关于x的一次函数,其中k和b为常数。这样在一次函数中,只要确定了k和b的值,那么这个一次函数也就随之确定了。可以说k和b是确定一次函数的两个因素。
2.已知一次函数y=2x+1,x取何值时,函数值y=3?
令y=3,代入解析式,得3=2x+1,解得x=1。
例题讲解
类型一:一次函数的实际应用
温度的度量有两种:摄氏温度和华氏温度.
水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
例1
解:用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设C = kF + b,
由已知条件,得
212k + b =100,
32k + b = 0 .
{
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
巩固练习
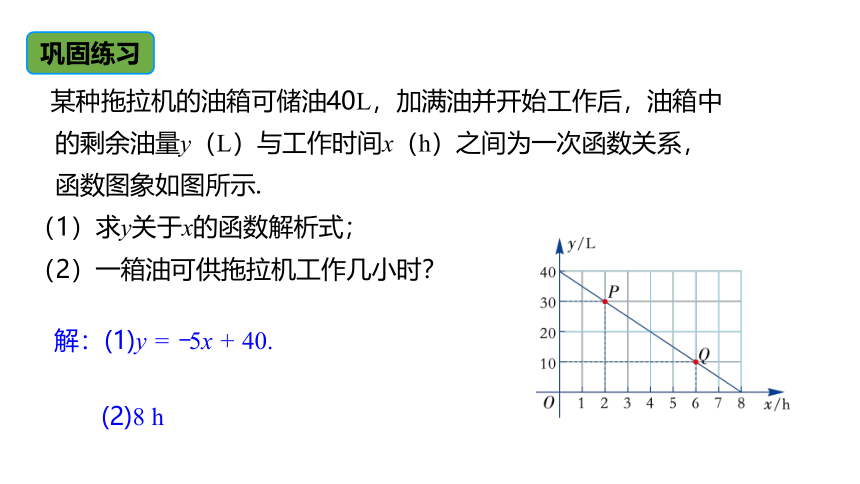
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h)之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数解析式;
(2)一箱油可供拖拉机工作几小时?
解:(1)y = -5x + 40.
(2)8 h
例2 黄金1号”玉米种子的价格为5元/kg.如果一次购买2 kg以上的种子,超过2 kg部分的种子价格打8折.
(1)填写下表.
(2)写出付款金额关于购买量的函数解析式,并画出函数图象.
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
类型二:分段函数的实际应用
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为: .
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
解:(1)
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 2.5 5 7.5 10 12 14 16 18 …
(2) 设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
y =
5x(0≤x≤2)
4x+2(x>2)
{
这样的函数叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
即:
的函数图象为:
y =
5x(0≤x≤2)
4x+2(x>2)
{
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
思考 你能由上面的函数解析式解决以下问题吗?由函数图象也能解决这些问题吗?
(1)一次购买1.5 kg种子,需付款多少元?
(2)一次购买3 kg种子,需付款多少元?
关键是根据自变量值所在的取值范围,选择对应的函数解析式带入即可或通过图象找到对应的函数值
当x=1.5时,y=5×1.5=7.5(元).
当x=3时,y=4×3+2=14(元).
巩固练习
为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:y关于x的函数解析式为:
(1+0.3)x =1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2. (x>8)
y=
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)∵1.3×8=10.4<26.6,∴该用户用水量超过8立方米.
∴2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14立方米.
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
随堂演练
1.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经过几个月才能存够200元?
40
80
120
y/元
x/月
1
2
3
4
5
o
解: (1)设函数解析式为y=kx+b,
由图可知图象过(0,40),(4,120)
∴这个函数的解析式为y=20x+40.
(2)当y=200时,20x+40=200, 解得x=8
∴小明经过8个月才能存够200元
解得
∴
40
80
120
y/元
x/月
1
2
3
4
5
o
解:(1)由题意得
当0≤t≤2时,T=20;
当2函数解析式为:
T =
20(0≤t≤2)
5t+10(22.一个试验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
{
T=20(0≤t≤2)
T=5t+10(220
10
40
T/℃
t/h
O
1
2
30
4
3
(2)函数图像为:
课堂小结
一次函数与实际问题
一次函数与实际问题;
分段函数的解析式与图象.
第十九章 一次函数
19.2.2 第4课时 一次函数的实际应用
知识回顾
1.什么是一次函数?确定一个一次函数需要几个因素? 是哪几个?
y=kx+b(k≠0)叫做关于x的一次函数,其中k和b为常数。这样在一次函数中,只要确定了k和b的值,那么这个一次函数也就随之确定了。可以说k和b是确定一次函数的两个因素。
2.已知一次函数y=2x+1,x取何值时,函数值y=3?
令y=3,代入解析式,得3=2x+1,解得x=1。
例题讲解
类型一:一次函数的实际应用
温度的度量有两种:摄氏温度和华氏温度.
水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
例1
解:用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设C = kF + b,
由已知条件,得
212k + b =100,
32k + b = 0 .
{
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
巩固练习
某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h)之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数解析式;
(2)一箱油可供拖拉机工作几小时?
解:(1)y = -5x + 40.
(2)8 h
例2 黄金1号”玉米种子的价格为5元/kg.如果一次购买2 kg以上的种子,超过2 kg部分的种子价格打8折.
(1)填写下表.
(2)写出付款金额关于购买量的函数解析式,并画出函数图象.
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
类型二:分段函数的实际应用
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为: .
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
解:(1)
购买量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 2.5 5 7.5 10 12 14 16 18 …
(2) 设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
y =
5x(0≤x≤2)
4x+2(x>2)
{
这样的函数叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
即:
的函数图象为:
y =
5x(0≤x≤2)
4x+2(x>2)
{
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
思考 你能由上面的函数解析式解决以下问题吗?由函数图象也能解决这些问题吗?
(1)一次购买1.5 kg种子,需付款多少元?
(2)一次购买3 kg种子,需付款多少元?
关键是根据自变量值所在的取值范围,选择对应的函数解析式带入即可或通过图象找到对应的函数值
当x=1.5时,y=5×1.5=7.5(元).
当x=3时,y=4×3+2=14(元).
巩固练习
为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:y关于x的函数解析式为:
(1+0.3)x =1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2. (x>8)
y=
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)∵1.3×8=10.4<26.6,∴该用户用水量超过8立方米.
∴2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14立方米.
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
随堂演练
1.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经过几个月才能存够200元?
40
80
120
y/元
x/月
1
2
3
4
5
o
解: (1)设函数解析式为y=kx+b,
由图可知图象过(0,40),(4,120)
∴这个函数的解析式为y=20x+40.
(2)当y=200时,20x+40=200, 解得x=8
∴小明经过8个月才能存够200元
解得
∴
40
80
120
y/元
x/月
1
2
3
4
5
o
解:(1)由题意得
当0≤t≤2时,T=20;
当2
T =
20(0≤t≤2)
5t+10(2
{
T=20(0≤t≤2)
T=5t+10(2
10
40
T/℃
t/h
O
1
2
30
4
3
(2)函数图像为:
课堂小结
一次函数与实际问题
一次函数与实际问题;
分段函数的解析式与图象.
