2021-2022学年九年级数学人教版下册 28.1.3 特殊角的三角函数值 课件(共22张)
文档属性
| 名称 | 2021-2022学年九年级数学人教版下册 28.1.3 特殊角的三角函数值 课件(共22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 18:45:44 | ||
图片预览




文档简介
(共22张PPT)
28.1.3 特殊角的三角函数值
学习目标
1)理解30°,45°,60°角的三角函数值的推导方法以及角与数值的对应关系
2)掌握特殊角的三角函数值的计算与简单的应用.
3)领会模型思想,数学结合,方程思想和函数思想在解决问题中的应用。
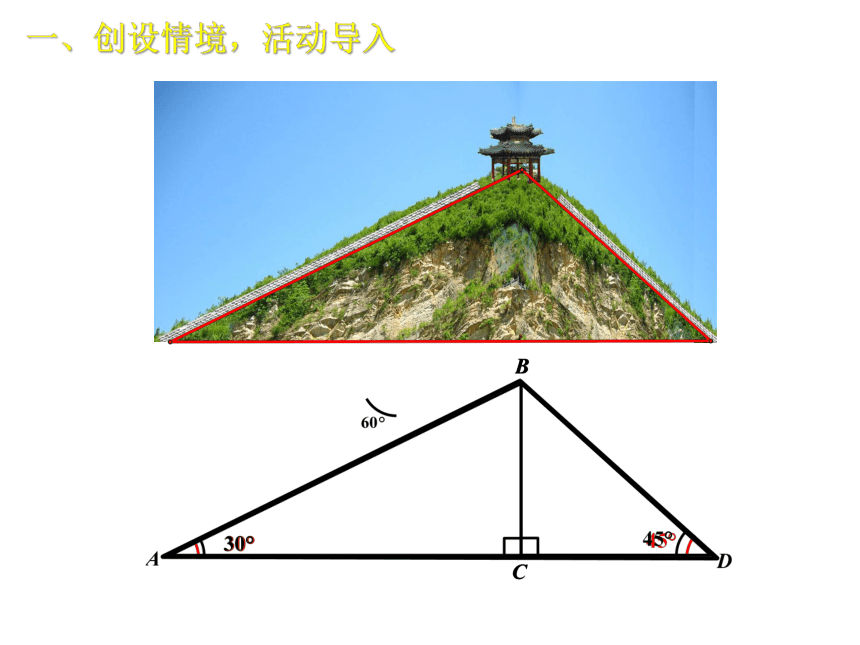
育才中学筹备“庆圣诞、迎新年”登山活动,山的东西两面各有一条石阶路通向山顶,东坡坡面与水平地面所成的夹角为45°,西坡坡面与水平地面所成的夹角为30°.学校筹备小组准备在东西两坡上设置一些小彩旗,并给每位参与登山活动的同学发一个圣诞帽.
西坡出发地
东坡出发地
请问:在上述的登山图中, 可以抽象出什么几何图形
一、创设情境,活动导入
一、创设情境,活动导入
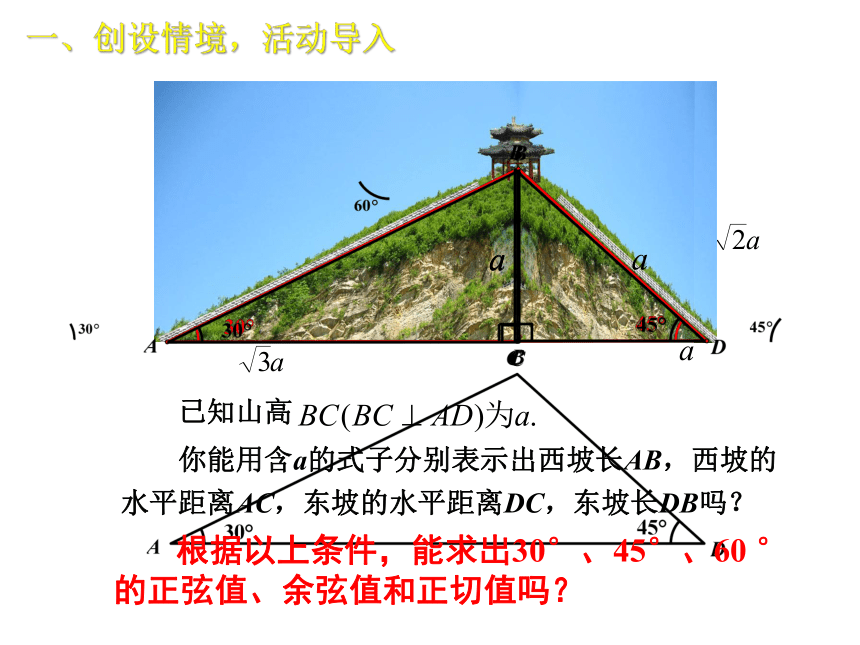
已知山高
a
a
a
根据以上条件,能求出30°、45°、60 °的正弦值、余弦值和正切值吗?
你能用含a的式子分别表示出西坡长AB,西坡的水平距离AC,东坡的水平距离DC,东坡长DB吗?
一、创设情境,活动导入
二、自主探究,获取特值
问题1:观察一副三角尺有几个锐角? 他们分别是多少度
2: 等于多少?你是怎么得到的?
3. 等于多少 呢?
4.还有两个特殊的角他们的三角函数值分别是多少?
锐角 三角函数 30° 45° 60°
特殊角的三角函值表
这张表蕴含了丰富的数学特性哟!
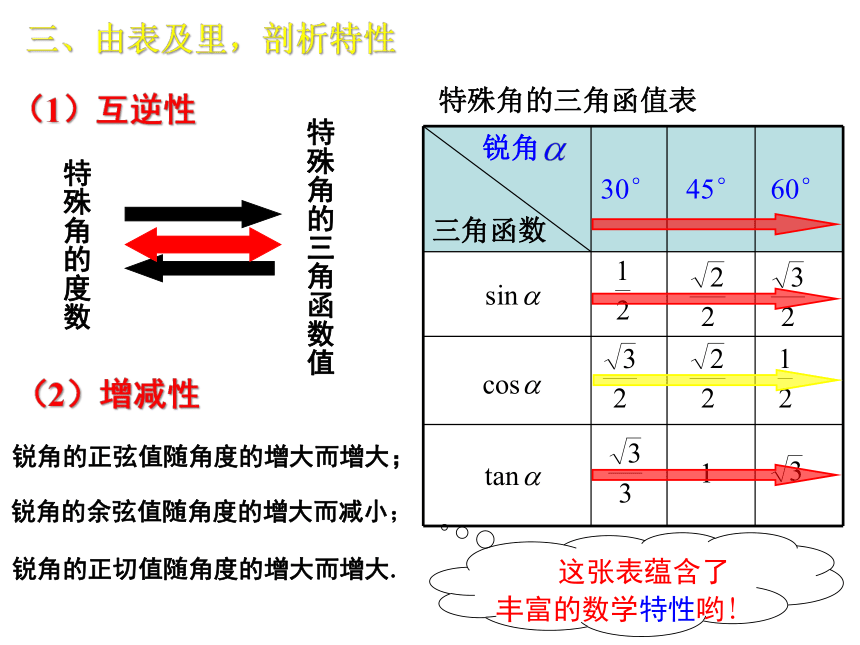
锐角的正弦值随角度的增大而增大;
特殊角的度数
(1)互逆性
(2)增减性
特殊角的三角函数值
锐角的余弦值随角度的增大而减小;
锐角的正切值随角度的增大而增大.
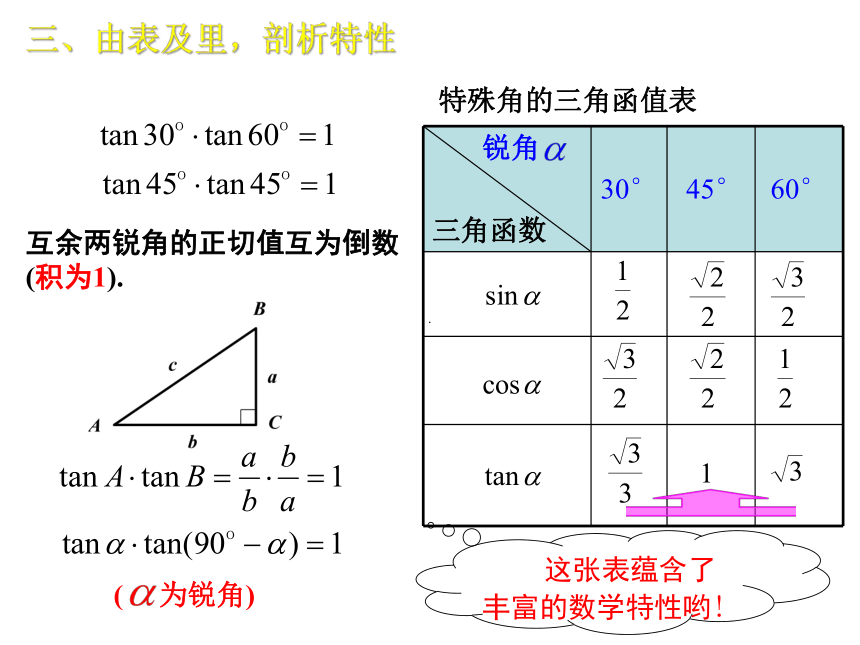
三、由表及里,剖析特性
锐角 三角函数 30° 45° 60°
特殊角的三角函值表
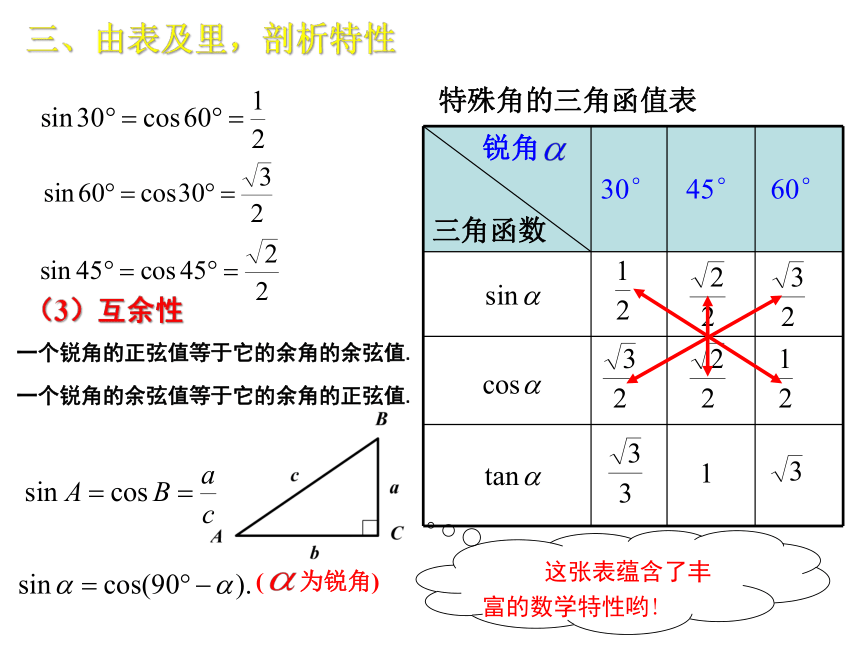
一个锐角的正弦值等于它的余角的余弦值.
这张表蕴含了丰富的数学特性哟!
一个锐角的余弦值等于它的余角的正弦值.
( 为锐角)
三、由表及里,剖析特性
(3)互余性
锐角 三角函数 30° 45° 60°
特殊角的三角函值表
互余两锐角的正切值互为倒数
(积为1).
这张表蕴含了丰富的数学特性哟!
( 为锐角)
三、由表及里,剖析特性
1. 同角三角函数关系
(1)平方关系:
(2)商除关系:
2. 互余的两角之间的三角函数关系:
若∠A+∠B=90°,则sinA cosB,cosA sinB,
tanA · tanB = .
=
=
1
三角函数间的关系
1.求下列各式的值:
◆温馨提示:
四、初步应用,发掘特质
2.育才中学在筹备“庆圣诞、迎新年”登山活动中,准备了
一些直角三角形的小彩旗和一些发给参与登山活动同学的
圆锥形圣诞帽.
(1)如图1为一个直角三角形的小彩旗,即Rt
思路点拨:
图1
四、初步应用,发掘特质
(2)如图2为一个圆锥形的圣诞帽,已知圆锥的
高AO等于圆锥的底面半径OB的
思路点拨:
AO等于
OB的
四、初步应用,发掘特质
(2)如图2为一个圆锥形的圣诞帽,已知圆锥的
高AO等于圆锥的底面半径OB的
思路点拨:
四、初步应用,发掘特质
3.(1)小明测得这座山的西坡长AB为1000米,山高为500米,请问西坡坡面与水平地面所成的夹角 为多少度
作BC⊥AD于C,
则BC为山高,BC=500米,
思路点拨:
解:
五、拓宽思路,灵活应用
4.(2)在第(1)问的条件下,
500
思路点拨:
解:
六、拓宽思路,灵活应用
4.(3)在第(1)问的条件下,若∠D=35°,求DC的长.
500
解:
六、拓宽思路,灵活应用
5、如图,在 中, , , ,延长CB至点D,使
(1)求 的度数;
(2)求 的值。
(3)你还能求出哪些非特殊角的三角函数值?
A
C
D
B
6、已知:如图,⊙O的半径OC= ,OC⊥AB于C点, 求:半径及AB的长
3.如图在⊙O中,OB为半径,BC是一条弦,
且OB=BC,则sinA= .
4.已知锐角A满足关系式
A.30° B.45° C. 60° D.不能确定
则∠A的度数为( ).
1.计算:
六、学习反思,达标检测
2.如果在△ABC中,∠C=90°sinA= ,那么sin 的值等于( )
5.已知 为锐角且 ,求 的值
6.如图,在△ABC中,∠A=30°, ,求 AB的长度.
A
B
C
2.思想方法
1.知识内容
数形结合、模型思想、方程思想、函数思想.
六、学习反思,达标检测
3.数学素养
数学运算、几何直观、数学抽象、数学建模
30°、45°、60°角的三角函数值
通过三角函数值求角度
28.1.3 特殊角的三角函数值
学习目标
1)理解30°,45°,60°角的三角函数值的推导方法以及角与数值的对应关系
2)掌握特殊角的三角函数值的计算与简单的应用.
3)领会模型思想,数学结合,方程思想和函数思想在解决问题中的应用。
育才中学筹备“庆圣诞、迎新年”登山活动,山的东西两面各有一条石阶路通向山顶,东坡坡面与水平地面所成的夹角为45°,西坡坡面与水平地面所成的夹角为30°.学校筹备小组准备在东西两坡上设置一些小彩旗,并给每位参与登山活动的同学发一个圣诞帽.
西坡出发地
东坡出发地
请问:在上述的登山图中, 可以抽象出什么几何图形
一、创设情境,活动导入
一、创设情境,活动导入
已知山高
a
a
a
根据以上条件,能求出30°、45°、60 °的正弦值、余弦值和正切值吗?
你能用含a的式子分别表示出西坡长AB,西坡的水平距离AC,东坡的水平距离DC,东坡长DB吗?
一、创设情境,活动导入
二、自主探究,获取特值
问题1:观察一副三角尺有几个锐角? 他们分别是多少度
2: 等于多少?你是怎么得到的?
3. 等于多少 呢?
4.还有两个特殊的角他们的三角函数值分别是多少?
锐角 三角函数 30° 45° 60°
特殊角的三角函值表
这张表蕴含了丰富的数学特性哟!
锐角的正弦值随角度的增大而增大;
特殊角的度数
(1)互逆性
(2)增减性
特殊角的三角函数值
锐角的余弦值随角度的增大而减小;
锐角的正切值随角度的增大而增大.
三、由表及里,剖析特性
锐角 三角函数 30° 45° 60°
特殊角的三角函值表
一个锐角的正弦值等于它的余角的余弦值.
这张表蕴含了丰富的数学特性哟!
一个锐角的余弦值等于它的余角的正弦值.
( 为锐角)
三、由表及里,剖析特性
(3)互余性
锐角 三角函数 30° 45° 60°
特殊角的三角函值表
互余两锐角的正切值互为倒数
(积为1).
这张表蕴含了丰富的数学特性哟!
( 为锐角)
三、由表及里,剖析特性
1. 同角三角函数关系
(1)平方关系:
(2)商除关系:
2. 互余的两角之间的三角函数关系:
若∠A+∠B=90°,则sinA cosB,cosA sinB,
tanA · tanB = .
=
=
1
三角函数间的关系
1.求下列各式的值:
◆温馨提示:
四、初步应用,发掘特质
2.育才中学在筹备“庆圣诞、迎新年”登山活动中,准备了
一些直角三角形的小彩旗和一些发给参与登山活动同学的
圆锥形圣诞帽.
(1)如图1为一个直角三角形的小彩旗,即Rt
思路点拨:
图1
四、初步应用,发掘特质
(2)如图2为一个圆锥形的圣诞帽,已知圆锥的
高AO等于圆锥的底面半径OB的
思路点拨:
AO等于
OB的
四、初步应用,发掘特质
(2)如图2为一个圆锥形的圣诞帽,已知圆锥的
高AO等于圆锥的底面半径OB的
思路点拨:
四、初步应用,发掘特质
3.(1)小明测得这座山的西坡长AB为1000米,山高为500米,请问西坡坡面与水平地面所成的夹角 为多少度
作BC⊥AD于C,
则BC为山高,BC=500米,
思路点拨:
解:
五、拓宽思路,灵活应用
4.(2)在第(1)问的条件下,
500
思路点拨:
解:
六、拓宽思路,灵活应用
4.(3)在第(1)问的条件下,若∠D=35°,求DC的长.
500
解:
六、拓宽思路,灵活应用
5、如图,在 中, , , ,延长CB至点D,使
(1)求 的度数;
(2)求 的值。
(3)你还能求出哪些非特殊角的三角函数值?
A
C
D
B
6、已知:如图,⊙O的半径OC= ,OC⊥AB于C点, 求:半径及AB的长
3.如图在⊙O中,OB为半径,BC是一条弦,
且OB=BC,则sinA= .
4.已知锐角A满足关系式
A.30° B.45° C. 60° D.不能确定
则∠A的度数为( ).
1.计算:
六、学习反思,达标检测
2.如果在△ABC中,∠C=90°sinA= ,那么sin 的值等于( )
5.已知 为锐角且 ,求 的值
6.如图,在△ABC中,∠A=30°, ,求 AB的长度.
A
B
C
2.思想方法
1.知识内容
数形结合、模型思想、方程思想、函数思想.
六、学习反思,达标检测
3.数学素养
数学运算、几何直观、数学抽象、数学建模
30°、45°、60°角的三角函数值
通过三角函数值求角度
