人教课标版(B版)高中数学必修3《3.3.2随机数的含义与应用》参考课件(共26张PPT)
文档属性
| 名称 | 人教课标版(B版)高中数学必修3《3.3.2随机数的含义与应用》参考课件(共26张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 372.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
3.3.2 随机数的含义与应用
随机数就是在一定范围内随机产生的数,并且得到这个范围内的每一个数的机会一样,随机数应用很广泛,利用它可以帮助我们进行随机抽样,还可以利用它在某一个范围得到每一个数机会是均等的这一特征来模拟试验,这样可代替我们自己做大量重复的试验,从而使我们顺利地求出有关事件的概率。
随机数的产生可以人工产生,例如抽签、摸球、转盘等方法,但这样做费时、费力,而且有时很难确保抽到每一个数的机会是均等的.
因此,我们现在主要是通过计算器和计算机来产生随机数的。
现在大部分计算器都能产生0~1之间的均匀随机数(实数)。
(1)用函数型计算器产生随机数的方法:
按一次SHIFT+RAN#键产生一个0~1之间的随机数,若需要多个,则重复按键;
(2)计算机中用软件产生随机数(本书用Scilab产生随机数):
①Scilab中用rand( )函数来产生0~1的均匀随机数,每调用一次rand( )函数,就产生一个随机数。
②若要产生a~b之间的随机数,可以使用变换rand( )*(b-a)+a得到.
(3)在Excel工作表中得到随机数
在Excel工作表中,在单元格中输入“=rand( )”就得到一个0~1之间的随机数。
例1. 随机模拟投掷硬币的试验,估计掷得正面的概率。
解:用计算器产生一个0~1之间的随机数,如果这个数在0~0.5之间,则认为硬币正面向上,如果这个随机数在0.5~1之间,则认为硬币正面向下。
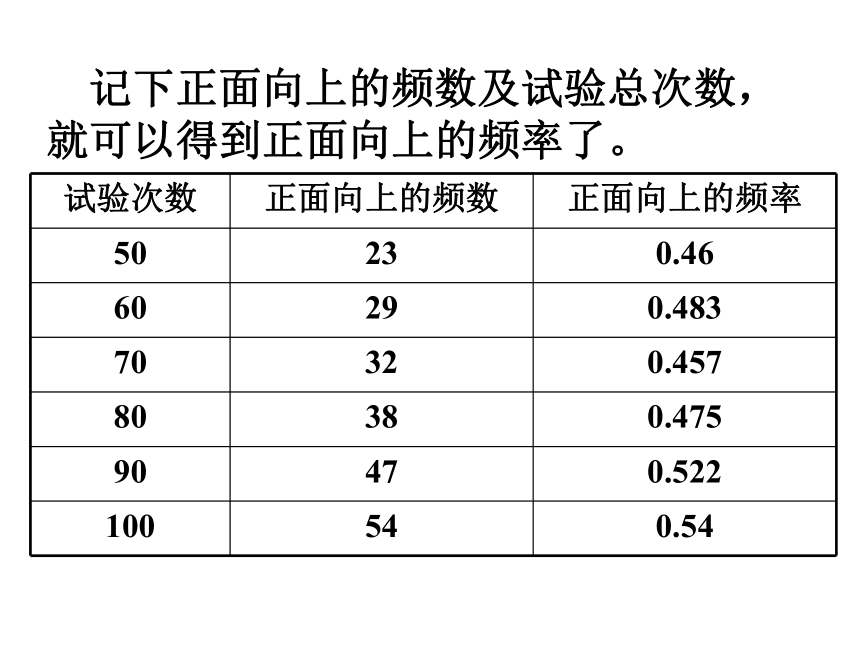
记下正面向上的频数及试验总次数,就可以得到正面向上的频率了。
试验次数 正面向上的频数 正面向上的频率
50 23 0.46
60 29 0.483
70 32 0.457
80 38 0.475
90 47 0.522
100 54 0.54
例2. 随机模拟3.3.1中例3海豚在水池中自由游弋的试验,并估计事件A:“海豚嘴尖离岸边不超过2m”的概率。
我们利用计算机产生随机数x和y,用它们来表示海豚嘴尖的横坐标与纵坐标,如果(x,y)出现在图中的阴影部分,我们就认为事件A发生了。
下面我们设计一个算法使计算机或计算器能模拟这个试验并根据事件A发生的概率.
S1 用计数器n记录做了多少次试验,用计数器m记录其中有多少次 (x,y)出现在阴影部分中,首先置n=0,m=0;
S2 用变换rand( )*30-15产生-15~15之间的随机数x作为海豚嘴尖的横坐标,用变换rand( )*20-10产生-10~10之间的随机数y作为海豚嘴尖的纵坐标;
S3 判断(x,y)是否落在阴影部分中,即是否满足||x|-15|≤2或||y|-10|≤2,如果是,则m=m+1,如果不是,则m不变;
S4 表示随机试验次数的计数器n值加1,即n=n+1, 如果还需要试验,则返回步骤S2继续执行,否则,程序结束。
程序结束后,事件A发生的频率 作为A的概率近似值。
试验次数 事件A频数m 事件A频率m/n
100 35 0.35
1000 324 0.324
10000 2997 0.2997
100000 30506 0.30506
N=input(“N=");
n=0;m=0;
for i=1:1:N
x=rand()*30-15;
y=rand()*20-10;
c=abs(abs(x)-15);
d=abs(abs(y)-10);
if c<=2|d<=2
m=m+1;
end
n=n+1;
end
p=m/N;
p
例3.利用随机数和几何概型求π的近似值.
在下图所示的边长为2的正方形中随机撒一大把豆子,计算落在正方形的内切圆中的豆子数与落在正方形中的豆子数之比,并以此估计圆周率π的值.
如果我们把“在正方形中撒豆子”看成试验,把“豆子落在圆中”看成随机事件A.
则落在圆中的豆子数与落在正方形中的豆子数的比值就是事件A发生的频率.当我们撒一大把豆子时,这时频率可以近似地看成事件A 的概率,可以认为这是一个几何概型问题.
解:由几何概型的计算公式,得
P(A)= —————
圆面积
正方形面积
所以π= 4×P(A ) .
我们在正方形中撒了n颗豆子,其中有m颗落在圆中,则圆周率π的近似值等于
用例2的类似办法,设计一个算法用计算机模拟这个撒豆子的试验。
S1 用计数器n记录做了多少次试验,用计数器m记录其中有多少颗豆子落入圆中,首先置n=0,m=0;
S2 用变换rand( )*2-1产生两个-1~1之间的随机数x和y,用它们来表示豆子的横坐标和纵坐标;
S3 判断(x,y)是否落在圆中,即是否满足x2+y2≤1,如果是,则计数器m=m+1,如果不是,则m不变;
S4 表示随机试验次数的计数器n值加1,即n=n+1, 如果还需要试验,则返回步骤S2继续执行,否则,程序结束。
程序结束后,计算 作为π的近似值.
N=input(“N=");
n=0;m=0;
for i=1:1:N
x=rand()*2-1;
y=rand()*2-1;
c=x^2+y^2;
if c<=1
m=m+1;
end
n=n+1;
end
p=4*m/N;
p
例2与例3采用的基本方法是:建立一个概率模型,它与我们感兴趣的量有关。然后设计适当的试验,并通过这个试验结果来确定这些量。
按照以上思路建立起来的方法称为计算机随机模拟法或蒙特卡洛方法。
现在随着计算机科学与技术的飞速发展,用计算机来模拟所设计的试验已经变得越来越普遍。
例4. 取一根长度为3m的绳子,拉直后在任意位置剪断,用随机模拟法估算剪得两段绳子的长度都不小于1m的概率有多大
解: 设事件A表示“剪得两段的长度都不小于1m”
S1 用计数器n记录做了多少次试验,用计数器m记录其中有多少次随机数x出现在1~2之间(即剪得两段绳子的长度都不小于1m)。首先置n=0,m=0;
S2 用变换rand()*3产生0~3之间的均匀随机数;
S3 判断剪得的两段绳子长度是否都大于1,即是否满足1S4 表示随机试验次数的计数器n的值加1,即n=n+1,如果还要继续试验,则返回步骤S2继续执行,否则,程序结束;
程序结束后事件A发生的频率 作为事件A的概率的近似值 .
例5. 利用随机模拟法近似计算图中阴影部分(曲线y=2x与x=±1及x轴围成的图形)的面积.
解:在坐标系中画出正方形,用随机模拟的方法可以求出阴影部分与正方形面积之比,从而求得阴影部分面积的近似值。
S1 用计数器n记录做了多少次投点试验,用计数器m记录其中有多少个(x,y)满足-1S2 用变换rand( )*2-1产生-1~1之间的均匀随机数x表示所投的点的横坐标;用变量rand( )*2产生0~2之间的均匀随机数y表示所投的点的纵坐标;
S3 判断点是否落在阴影部分,即是否满足0S4 表示随机试验次数的计数器n的值加1,即n=n+1,如果还要继续试验,则返回步骤S2继续执行,否则,程序结束;
程序结束后事件A发生的频率 作为事件A的概率的近似值。
设阴影部分的面积为S,正方形的面积为4,由几何概型计算公式得
所以
π的另一种求法
1777年法国科学家布丰做了一个投针试验,这个试验被认为是几何概型的第一个试验。他在一张大纸上画了一些平行线,相邻两条平行线间的距离都相等。再把长度等于平行线间距离一半的针投到纸上,并记录投针的总次数及针落到纸上与平行线中的某一条相交的次数,共计投针2212次,其中与平行线相交的有704次,发现它们的商2212÷ 704≈3.142045与π非常接近。
以后又有多位数学家重复做过投针试验,都得到了类似的结果。那么,投针试验为什么能算出π的近似值呢?
如图,取一张大纸,在上面画上一组平行线,使相邻两平行线间距离都等于d,再取一个直径为d的铁丝圆圈。如果把这个铁丝圆圈投掷到纸上,
则圆圈与平行线组的交点肯定是2个,如果投掷n次,则交点总计应为2n.
如果把铁丝拉直(长度不变)再投掷到纸上,则铁丝与平行线组的交点就可能是0个、1个、2个或3个。
布丰认为,既然两根铁丝长度相等,在大量重复试验时,它们与同一平行线的交点总数应是相等的。如果也投掷n次,则交点总计也应与2n相差甚小。再考虑铁丝上的每个点,它是否落在平行线组的某一条上也是机会均等的。
现在如果取一段长为l的铁丝,则投掷n次时,交点总数n’应与 相差甚小。即如果一根长度为l的铁丝投掷n次,得到交点总数为n’= .
故当投掷次数n较大时, 应在π附近摆动。布丰取l= ,则 应在π附近摆动。布丰试验的结果正好反映了这一事实。
3.3.2 随机数的含义与应用
随机数就是在一定范围内随机产生的数,并且得到这个范围内的每一个数的机会一样,随机数应用很广泛,利用它可以帮助我们进行随机抽样,还可以利用它在某一个范围得到每一个数机会是均等的这一特征来模拟试验,这样可代替我们自己做大量重复的试验,从而使我们顺利地求出有关事件的概率。
随机数的产生可以人工产生,例如抽签、摸球、转盘等方法,但这样做费时、费力,而且有时很难确保抽到每一个数的机会是均等的.
因此,我们现在主要是通过计算器和计算机来产生随机数的。
现在大部分计算器都能产生0~1之间的均匀随机数(实数)。
(1)用函数型计算器产生随机数的方法:
按一次SHIFT+RAN#键产生一个0~1之间的随机数,若需要多个,则重复按键;
(2)计算机中用软件产生随机数(本书用Scilab产生随机数):
①Scilab中用rand( )函数来产生0~1的均匀随机数,每调用一次rand( )函数,就产生一个随机数。
②若要产生a~b之间的随机数,可以使用变换rand( )*(b-a)+a得到.
(3)在Excel工作表中得到随机数
在Excel工作表中,在单元格中输入“=rand( )”就得到一个0~1之间的随机数。
例1. 随机模拟投掷硬币的试验,估计掷得正面的概率。
解:用计算器产生一个0~1之间的随机数,如果这个数在0~0.5之间,则认为硬币正面向上,如果这个随机数在0.5~1之间,则认为硬币正面向下。
记下正面向上的频数及试验总次数,就可以得到正面向上的频率了。
试验次数 正面向上的频数 正面向上的频率
50 23 0.46
60 29 0.483
70 32 0.457
80 38 0.475
90 47 0.522
100 54 0.54
例2. 随机模拟3.3.1中例3海豚在水池中自由游弋的试验,并估计事件A:“海豚嘴尖离岸边不超过2m”的概率。
我们利用计算机产生随机数x和y,用它们来表示海豚嘴尖的横坐标与纵坐标,如果(x,y)出现在图中的阴影部分,我们就认为事件A发生了。
下面我们设计一个算法使计算机或计算器能模拟这个试验并根据事件A发生的概率.
S1 用计数器n记录做了多少次试验,用计数器m记录其中有多少次 (x,y)出现在阴影部分中,首先置n=0,m=0;
S2 用变换rand( )*30-15产生-15~15之间的随机数x作为海豚嘴尖的横坐标,用变换rand( )*20-10产生-10~10之间的随机数y作为海豚嘴尖的纵坐标;
S3 判断(x,y)是否落在阴影部分中,即是否满足||x|-15|≤2或||y|-10|≤2,如果是,则m=m+1,如果不是,则m不变;
S4 表示随机试验次数的计数器n值加1,即n=n+1, 如果还需要试验,则返回步骤S2继续执行,否则,程序结束。
程序结束后,事件A发生的频率 作为A的概率近似值。
试验次数 事件A频数m 事件A频率m/n
100 35 0.35
1000 324 0.324
10000 2997 0.2997
100000 30506 0.30506
N=input(“N=");
n=0;m=0;
for i=1:1:N
x=rand()*30-15;
y=rand()*20-10;
c=abs(abs(x)-15);
d=abs(abs(y)-10);
if c<=2|d<=2
m=m+1;
end
n=n+1;
end
p=m/N;
p
例3.利用随机数和几何概型求π的近似值.
在下图所示的边长为2的正方形中随机撒一大把豆子,计算落在正方形的内切圆中的豆子数与落在正方形中的豆子数之比,并以此估计圆周率π的值.
如果我们把“在正方形中撒豆子”看成试验,把“豆子落在圆中”看成随机事件A.
则落在圆中的豆子数与落在正方形中的豆子数的比值就是事件A发生的频率.当我们撒一大把豆子时,这时频率可以近似地看成事件A 的概率,可以认为这是一个几何概型问题.
解:由几何概型的计算公式,得
P(A)= —————
圆面积
正方形面积
所以π= 4×P(A ) .
我们在正方形中撒了n颗豆子,其中有m颗落在圆中,则圆周率π的近似值等于
用例2的类似办法,设计一个算法用计算机模拟这个撒豆子的试验。
S1 用计数器n记录做了多少次试验,用计数器m记录其中有多少颗豆子落入圆中,首先置n=0,m=0;
S2 用变换rand( )*2-1产生两个-1~1之间的随机数x和y,用它们来表示豆子的横坐标和纵坐标;
S3 判断(x,y)是否落在圆中,即是否满足x2+y2≤1,如果是,则计数器m=m+1,如果不是,则m不变;
S4 表示随机试验次数的计数器n值加1,即n=n+1, 如果还需要试验,则返回步骤S2继续执行,否则,程序结束。
程序结束后,计算 作为π的近似值.
N=input(“N=");
n=0;m=0;
for i=1:1:N
x=rand()*2-1;
y=rand()*2-1;
c=x^2+y^2;
if c<=1
m=m+1;
end
n=n+1;
end
p=4*m/N;
p
例2与例3采用的基本方法是:建立一个概率模型,它与我们感兴趣的量有关。然后设计适当的试验,并通过这个试验结果来确定这些量。
按照以上思路建立起来的方法称为计算机随机模拟法或蒙特卡洛方法。
现在随着计算机科学与技术的飞速发展,用计算机来模拟所设计的试验已经变得越来越普遍。
例4. 取一根长度为3m的绳子,拉直后在任意位置剪断,用随机模拟法估算剪得两段绳子的长度都不小于1m的概率有多大
解: 设事件A表示“剪得两段的长度都不小于1m”
S1 用计数器n记录做了多少次试验,用计数器m记录其中有多少次随机数x出现在1~2之间(即剪得两段绳子的长度都不小于1m)。首先置n=0,m=0;
S2 用变换rand()*3产生0~3之间的均匀随机数;
S3 判断剪得的两段绳子长度是否都大于1,即是否满足1
程序结束后事件A发生的频率 作为事件A的概率的近似值 .
例5. 利用随机模拟法近似计算图中阴影部分(曲线y=2x与x=±1及x轴围成的图形)的面积.
解:在坐标系中画出正方形,用随机模拟的方法可以求出阴影部分与正方形面积之比,从而求得阴影部分面积的近似值。
S1 用计数器n记录做了多少次投点试验,用计数器m记录其中有多少个(x,y)满足-1
S3 判断点是否落在阴影部分,即是否满足0
程序结束后事件A发生的频率 作为事件A的概率的近似值。
设阴影部分的面积为S,正方形的面积为4,由几何概型计算公式得
所以
π的另一种求法
1777年法国科学家布丰做了一个投针试验,这个试验被认为是几何概型的第一个试验。他在一张大纸上画了一些平行线,相邻两条平行线间的距离都相等。再把长度等于平行线间距离一半的针投到纸上,并记录投针的总次数及针落到纸上与平行线中的某一条相交的次数,共计投针2212次,其中与平行线相交的有704次,发现它们的商2212÷ 704≈3.142045与π非常接近。
以后又有多位数学家重复做过投针试验,都得到了类似的结果。那么,投针试验为什么能算出π的近似值呢?
如图,取一张大纸,在上面画上一组平行线,使相邻两平行线间距离都等于d,再取一个直径为d的铁丝圆圈。如果把这个铁丝圆圈投掷到纸上,
则圆圈与平行线组的交点肯定是2个,如果投掷n次,则交点总计应为2n.
如果把铁丝拉直(长度不变)再投掷到纸上,则铁丝与平行线组的交点就可能是0个、1个、2个或3个。
布丰认为,既然两根铁丝长度相等,在大量重复试验时,它们与同一平行线的交点总数应是相等的。如果也投掷n次,则交点总计也应与2n相差甚小。再考虑铁丝上的每个点,它是否落在平行线组的某一条上也是机会均等的。
现在如果取一段长为l的铁丝,则投掷n次时,交点总数n’应与 相差甚小。即如果一根长度为l的铁丝投掷n次,得到交点总数为n’= .
故当投掷次数n较大时, 应在π附近摆动。布丰取l= ,则 应在π附近摆动。布丰试验的结果正好反映了这一事实。
