物理人教版 (2019)必修第二册6.3 向心加速度(共15张ppt)
文档属性
| 名称 | 物理人教版 (2019)必修第二册6.3 向心加速度(共15张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-08 08:58:03 | ||
图片预览




文档简介
(共15张PPT)
第六章 圆周运动
6.3 向心加速度
合力一定不为0,加速度一定不为0。
如何确定天宫二号空间实验室在轨飞行时加速度的方向和大小呢
天宫二号空间实验室在轨飞行时,
近似绕地球做匀速圆周运动。
线速度大小不变,但方向时刻变化
新课导入
温故知新
如何求:加速度
方法一:
加速度方向与 F 的方向相同
方法二:
v1
Δv
v2
一. 匀速圆周运动加速度
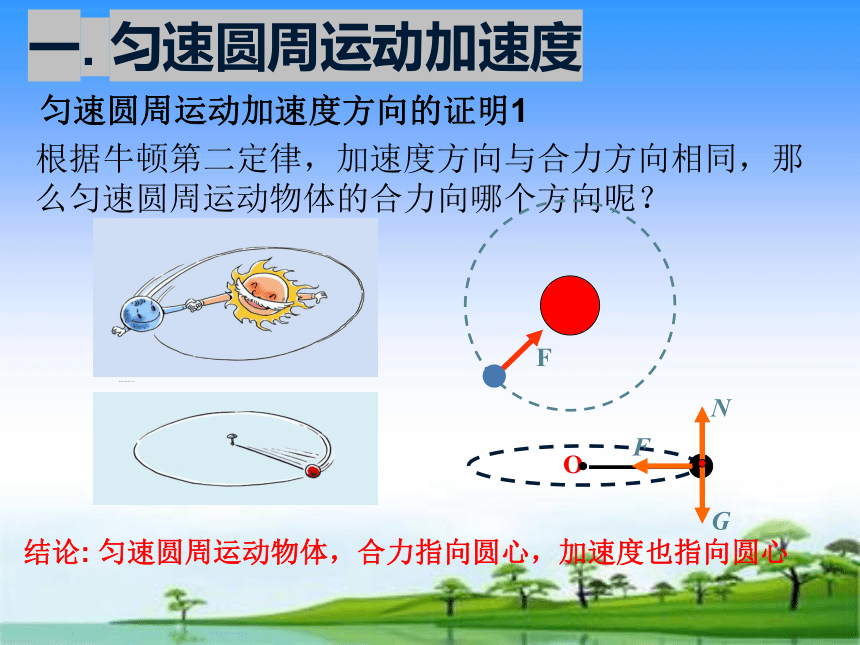
根据牛顿第二定律,加速度方向与合力方向相同,那么匀速圆周运动物体的合力向哪个方向呢?
图 5.6-1 地球受力沿什么方向?
F
F
O
G
N
结论: 匀速圆周运动物体,合力指向圆心,加速度也指向圆心
匀速圆周运动加速度方向的证明1
匀速圆周运动加速度方向的证明2
Δv
vB
vA
Δv
B
vB
vA
Δv
B
vB
vA
vA
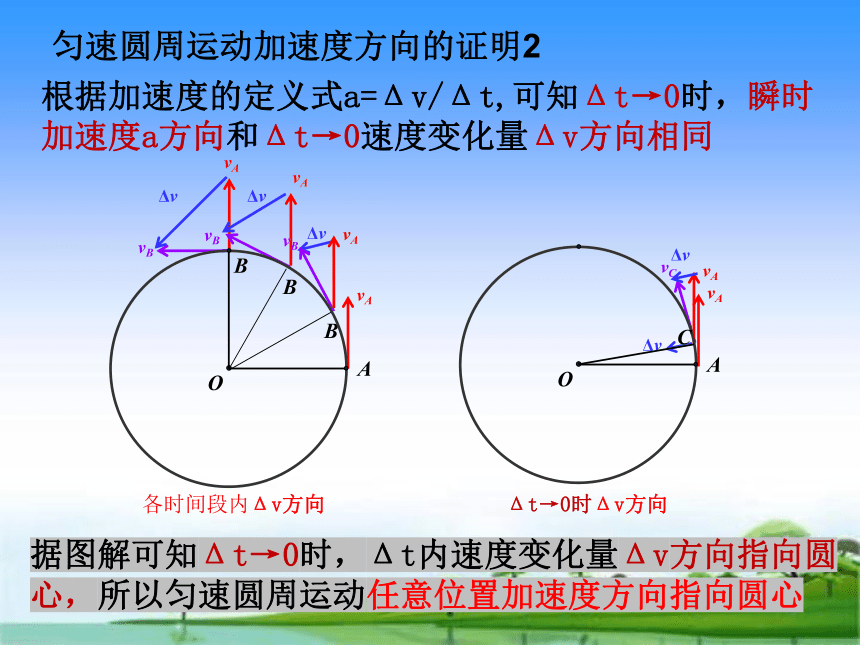
据图解可知Δt→0时,Δt内速度变化量Δv方向指向圆心,所以匀速圆周运动任意位置加速度方向指向圆心
根据加速度的定义式a=Δv/Δt,可知Δt→0时,瞬时加速度a方向和Δt→0速度变化量Δv方向相同
vA
vC
vA
Δv
Δv
O
A
B
各时间段内Δv方向
O
A
C
Δt→0时Δv方向
(1)定义:做匀速圆周运动的物体任意位置的加速度方向指向圆心,这个加速度称为向心加速度
(4)物理意义:描述速度方向变化的快慢(向心加速度只改变速度方向,不改变速度大小. )
(2)符号:an
(3)方向:始终指向圆心(与线速度方向垂直)
(5)说明:匀速圆周运动加速度的大小不变,方向时刻改变,所以匀速圆周运动不是匀变速运动,是变加速运动
1.向心加速度
(6)大小:
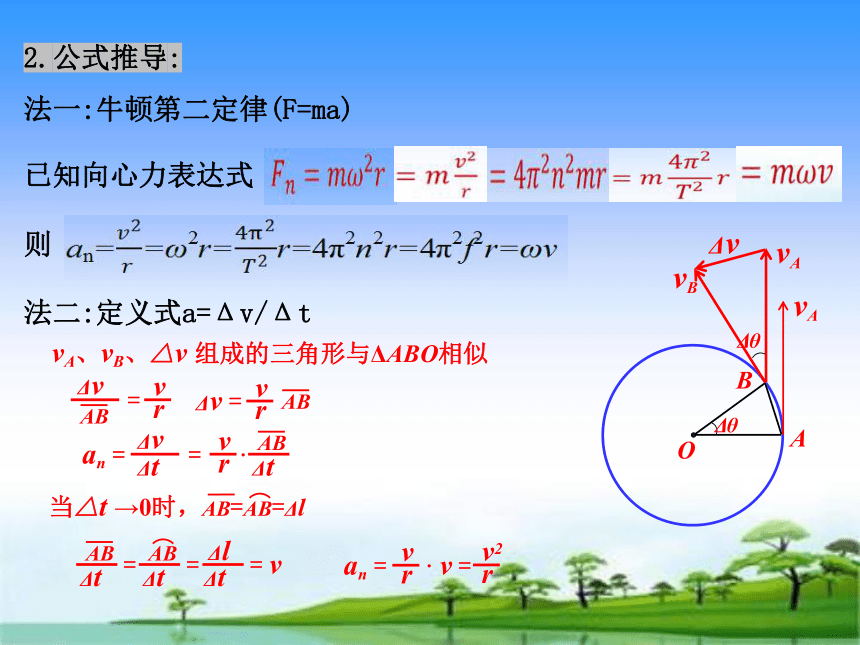
2.公式推导:
法一:牛顿第二定律(F=ma)
已知向心力表达式
则
法二:定义式a=Δv/Δt
O
B
A
vA
vB
vA
Δv
Δ
θ
Δ
θ
=
AB
Δv
v
r
vA、vB、△v 组成的三角形与ΔABO相似
Δv =
AB
v
r
an = = ·
AB
v
r
Δv
Δt
Δt
当△t →0时,AB=AB=Δl
an = · v =
v
r
v2
r
Δl
= = = v
AB
Δt
Δt
AB
Δt
3.向心加速度与半径的关系:
自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点 A、B、C,如图 6.3-2 所示。其中哪两点向心加
速度的关系适用于“向心加速度与半径成正比”,哪两点适用于“向心加速度与半径成反比”?给出解释。
思考与讨论
二、变速圆周运动的加速度
1.变速圆周运动合力与向心力
(1)合力一般不再指向圆心,与线速度一般也不垂直
(2)合力一般不等于向心力,向心力一般只是指向圆心的分力
1.变速圆周运动加速度与向心加速度
(1)合加速度一般不再指向圆心,与线速度一般也不垂直
(2)合加速度一般不等于an,an一般只是指向圆心的分加速度
(3)an改变速度方向,at改变速度大小.
ω
Fn
F
Ft
【例题1】如图6.3-3所示,在长为L的细绳下端拴一个质量为m的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就沿圆锥面旋转,这样就成了一个圆锥摆。当绳子跟竖直方向的夹角为θ时,小球运动的向心加速度an的大小为多少 通过计算说明:要增大夹角θ,应该增大小球运动的角速度。
解 根据对小球的受力分析,可得小球的向心力
Fn=mgtanθ
根据牛顿第二定律可得小球运动向心加速度
an=
=gtanθ
根据几何关系可知小球圆周运动半径
r=lsinθ
又an=ω2r,得cosθ=
从此式可以看出,当小球运动角速度增大时,夹角也随之增大。因此,要增大夹角θ,应该增大小球运动的角速度ω。
【例题2】已知地球半径R=6400km,自转周期T=24h,试计算在地球赤道和北纬300地区物体的向心加速度大小
①
②
A
O
R
r
(1)确定研究对象
(2)运动分析:确定运动性质、轨道平面,圆心和半径
(据几何关系求半径)
(3)受力分析:求合力和向心力
(4)据牛顿第二定律列式求解相关量
圆周运动动力学解题思路:
1、关于北京和广州随地球自转的向心加速度,下列说法中正确的是 ( )
A、它们的方向都沿半径指向地心
B、它们的方向都平行于赤道平面指向地轴
C、北京的向心加速度比广州的向心加速度大
D、北京的向心加速度比广州的向心加速度小
BD
2.如图所示,质量为m的木块从半径为R的半球形碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使木块的速率不变,那么下滑过程中 ( )
A.加速度为零,物块对碗面的压力大小不变
B.加速度恒定,物块对碗面的压力大小减小
C.加速度大小不变,方向时刻改变,但不一定指向圆心
D.加速度大小不变,方向时刻指向圆心,物块对碗面的压力大小增大。
D
课堂小结
第六章 圆周运动
6.3 向心加速度
合力一定不为0,加速度一定不为0。
如何确定天宫二号空间实验室在轨飞行时加速度的方向和大小呢
天宫二号空间实验室在轨飞行时,
近似绕地球做匀速圆周运动。
线速度大小不变,但方向时刻变化
新课导入
温故知新
如何求:加速度
方法一:
加速度方向与 F 的方向相同
方法二:
v1
Δv
v2
一. 匀速圆周运动加速度
根据牛顿第二定律,加速度方向与合力方向相同,那么匀速圆周运动物体的合力向哪个方向呢?
图 5.6-1 地球受力沿什么方向?
F
F
O
G
N
结论: 匀速圆周运动物体,合力指向圆心,加速度也指向圆心
匀速圆周运动加速度方向的证明1
匀速圆周运动加速度方向的证明2
Δv
vB
vA
Δv
B
vB
vA
Δv
B
vB
vA
vA
据图解可知Δt→0时,Δt内速度变化量Δv方向指向圆心,所以匀速圆周运动任意位置加速度方向指向圆心
根据加速度的定义式a=Δv/Δt,可知Δt→0时,瞬时加速度a方向和Δt→0速度变化量Δv方向相同
vA
vC
vA
Δv
Δv
O
A
B
各时间段内Δv方向
O
A
C
Δt→0时Δv方向
(1)定义:做匀速圆周运动的物体任意位置的加速度方向指向圆心,这个加速度称为向心加速度
(4)物理意义:描述速度方向变化的快慢(向心加速度只改变速度方向,不改变速度大小. )
(2)符号:an
(3)方向:始终指向圆心(与线速度方向垂直)
(5)说明:匀速圆周运动加速度的大小不变,方向时刻改变,所以匀速圆周运动不是匀变速运动,是变加速运动
1.向心加速度
(6)大小:
2.公式推导:
法一:牛顿第二定律(F=ma)
已知向心力表达式
则
法二:定义式a=Δv/Δt
O
B
A
vA
vB
vA
Δv
Δ
θ
Δ
θ
=
AB
Δv
v
r
vA、vB、△v 组成的三角形与ΔABO相似
Δv =
AB
v
r
an = = ·
AB
v
r
Δv
Δt
Δt
当△t →0时,AB=AB=Δl
an = · v =
v
r
v2
r
Δl
= = = v
AB
Δt
Δt
AB
Δt
3.向心加速度与半径的关系:
自行车的大齿轮、小齿轮、后轮的半径不一样,它们的边缘有三个点 A、B、C,如图 6.3-2 所示。其中哪两点向心加
速度的关系适用于“向心加速度与半径成正比”,哪两点适用于“向心加速度与半径成反比”?给出解释。
思考与讨论
二、变速圆周运动的加速度
1.变速圆周运动合力与向心力
(1)合力一般不再指向圆心,与线速度一般也不垂直
(2)合力一般不等于向心力,向心力一般只是指向圆心的分力
1.变速圆周运动加速度与向心加速度
(1)合加速度一般不再指向圆心,与线速度一般也不垂直
(2)合加速度一般不等于an,an一般只是指向圆心的分加速度
(3)an改变速度方向,at改变速度大小.
ω
Fn
F
Ft
【例题1】如图6.3-3所示,在长为L的细绳下端拴一个质量为m的小球,捏住绳子的上端,使小球在水平面内做圆周运动,细绳就沿圆锥面旋转,这样就成了一个圆锥摆。当绳子跟竖直方向的夹角为θ时,小球运动的向心加速度an的大小为多少 通过计算说明:要增大夹角θ,应该增大小球运动的角速度。
解 根据对小球的受力分析,可得小球的向心力
Fn=mgtanθ
根据牛顿第二定律可得小球运动向心加速度
an=
=gtanθ
根据几何关系可知小球圆周运动半径
r=lsinθ
又an=ω2r,得cosθ=
从此式可以看出,当小球运动角速度增大时,夹角也随之增大。因此,要增大夹角θ,应该增大小球运动的角速度ω。
【例题2】已知地球半径R=6400km,自转周期T=24h,试计算在地球赤道和北纬300地区物体的向心加速度大小
①
②
A
O
R
r
(1)确定研究对象
(2)运动分析:确定运动性质、轨道平面,圆心和半径
(据几何关系求半径)
(3)受力分析:求合力和向心力
(4)据牛顿第二定律列式求解相关量
圆周运动动力学解题思路:
1、关于北京和广州随地球自转的向心加速度,下列说法中正确的是 ( )
A、它们的方向都沿半径指向地心
B、它们的方向都平行于赤道平面指向地轴
C、北京的向心加速度比广州的向心加速度大
D、北京的向心加速度比广州的向心加速度小
BD
2.如图所示,质量为m的木块从半径为R的半球形碗口下滑到碗的最低点的过程中,如果由于摩擦力的作用使木块的速率不变,那么下滑过程中 ( )
A.加速度为零,物块对碗面的压力大小不变
B.加速度恒定,物块对碗面的压力大小减小
C.加速度大小不变,方向时刻改变,但不一定指向圆心
D.加速度大小不变,方向时刻指向圆心,物块对碗面的压力大小增大。
D
课堂小结
