2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程课件(15张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.2.3直线的一般式方程课件(15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 19:01:48 | ||
图片预览






文档简介
(共15张PPT)
2.2.3直线的一般式方程
名 称 几 何 条 件 方程 适用范围
点斜式
斜截式
两点式
截距式
点P(x0,y0)和斜率k
斜率k, y轴上的纵截距b
在x轴上的截距a在y轴上的截距b
P1(x1,y1),P2(x2,y2)
斜率存在
斜率存在
斜率存在,且不为0
斜率存在,且不为0,不经过原点
复习引入
思考:上述四种直线方程,能否写成如下统一形式?
x+ y+ =0
上述四式都可以写成直线方程的一般形式:Ax+By+C=0
探究新知
任意直线l,当l的斜率为k时,在其上任取一点P0(x0,y0),其方程为y-y0=k(x-x0),这是关于x、y的二元一次方程
当l的斜率不存在, 即直线l的倾斜角为90°时,直线的方程为x-x0=0,
上述方程可以认为是y的系数为0的二元一次方程
因此平面直角坐标系中的任意一条直线都可以用一个关于x、y的二元一次方程表示.
思考1 平面直角坐标系中的任意一条直线方程都可以用一个关于x,y的二元一次方程Ax+By+C=0表示吗?
探究新知
思考2 任意一个关于x,y 的二元一次方程Ax+By+C=0都表示一条直线吗?
探究新知
①当B≠0时,
②当B=0时,
这是直线的斜截式方程,它表示斜率是 ,
在y轴上的截距是 的直线.
表示垂直于x轴的一条直线
方程可化为
方程可化为
由上可知,关于x,y的二元一次方程都表示一条直线.
适用范围:
探究新知
任意一条直线
注意 : 对于直线方程的一般式,规定:
1)x的系数为正;
2)x,y的系数及常数项一般不出现分数;
3)按含x项,含y项、常数项顺序排列.
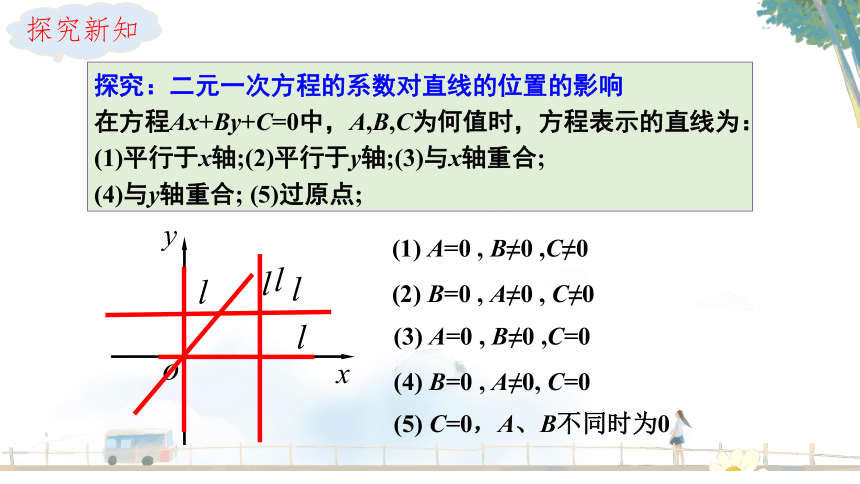
探究:二元一次方程的系数对直线的位置的影响
在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线为:
(1)平行于x轴;(2)平行于y轴;(3)与x轴重合;
(4)与y轴重合; (5)过原点;
(5) C=0,A、B不同时为0
探究新知
(1) A=0 , B≠0 ,C≠0
(2) B=0 , A≠0 , C≠0
(4) B=0 , A≠0, C=0
(3) A=0 , B≠0 ,C=0
典例分析
典例分析
O
x
y
1
1
2
3
4
2
A
B
结合例6,我们可以从几何角度看一个二元一次方程,即一个二元一次方程表示一条直线.
在代数中,我们研究了二元一次方程的解.因为二元一次方程的每一组解都可以看成平面直角坐标系中一个点的坐标,所以这个方程的全体解组成的集合,就是坐标满足二元一次方程的全体点的集合,这些点的集合组成一条直线.
平面直角坐标系是把二元一次方程和直线联系起来的桥梁,这是笛卡儿的伟大贡献.在平面直角坐标系中,任意一个二元一次方程是直角坐标平面上一条确定的直线;反之,直角坐标平面上的任意一条直线可以用一个确定的二元一次方程表示.
课堂练习
例3 直线
试讨论:(1) 的条件是什么?
(2) 的条件是什么?
典例分析
1.已知直线l1: x+(a+1)y-2+a=0和l2: 2ax+4y+16=0,若l1//l2,求a的值.
2. 已知直线l1: x-ay-1=0和l2: a2x+y+2=0,若l1⊥l2,求a的值.
a=1
a=1或a=0
小试牛刀
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
最后都要化成一般式Ax+By+C=0(A, B不同时为0)
课堂小结
2.2.3直线的一般式方程
名 称 几 何 条 件 方程 适用范围
点斜式
斜截式
两点式
截距式
点P(x0,y0)和斜率k
斜率k, y轴上的纵截距b
在x轴上的截距a在y轴上的截距b
P1(x1,y1),P2(x2,y2)
斜率存在
斜率存在
斜率存在,且不为0
斜率存在,且不为0,不经过原点
复习引入
思考:上述四种直线方程,能否写成如下统一形式?
x+ y+ =0
上述四式都可以写成直线方程的一般形式:Ax+By+C=0
探究新知
任意直线l,当l的斜率为k时,在其上任取一点P0(x0,y0),其方程为y-y0=k(x-x0),这是关于x、y的二元一次方程
当l的斜率不存在, 即直线l的倾斜角为90°时,直线的方程为x-x0=0,
上述方程可以认为是y的系数为0的二元一次方程
因此平面直角坐标系中的任意一条直线都可以用一个关于x、y的二元一次方程表示.
思考1 平面直角坐标系中的任意一条直线方程都可以用一个关于x,y的二元一次方程Ax+By+C=0表示吗?
探究新知
思考2 任意一个关于x,y 的二元一次方程Ax+By+C=0都表示一条直线吗?
探究新知
①当B≠0时,
②当B=0时,
这是直线的斜截式方程,它表示斜率是 ,
在y轴上的截距是 的直线.
表示垂直于x轴的一条直线
方程可化为
方程可化为
由上可知,关于x,y的二元一次方程都表示一条直线.
适用范围:
探究新知
任意一条直线
注意 : 对于直线方程的一般式,规定:
1)x的系数为正;
2)x,y的系数及常数项一般不出现分数;
3)按含x项,含y项、常数项顺序排列.
探究:二元一次方程的系数对直线的位置的影响
在方程Ax+By+C=0中,A,B,C为何值时,方程表示的直线为:
(1)平行于x轴;(2)平行于y轴;(3)与x轴重合;
(4)与y轴重合; (5)过原点;
(5) C=0,A、B不同时为0
探究新知
(1) A=0 , B≠0 ,C≠0
(2) B=0 , A≠0 , C≠0
(4) B=0 , A≠0, C=0
(3) A=0 , B≠0 ,C=0
典例分析
典例分析
O
x
y
1
1
2
3
4
2
A
B
结合例6,我们可以从几何角度看一个二元一次方程,即一个二元一次方程表示一条直线.
在代数中,我们研究了二元一次方程的解.因为二元一次方程的每一组解都可以看成平面直角坐标系中一个点的坐标,所以这个方程的全体解组成的集合,就是坐标满足二元一次方程的全体点的集合,这些点的集合组成一条直线.
平面直角坐标系是把二元一次方程和直线联系起来的桥梁,这是笛卡儿的伟大贡献.在平面直角坐标系中,任意一个二元一次方程是直角坐标平面上一条确定的直线;反之,直角坐标平面上的任意一条直线可以用一个确定的二元一次方程表示.
课堂练习
例3 直线
试讨论:(1) 的条件是什么?
(2) 的条件是什么?
典例分析
1.已知直线l1: x+(a+1)y-2+a=0和l2: 2ax+4y+16=0,若l1//l2,求a的值.
2. 已知直线l1: x-ay-1=0和l2: a2x+y+2=0,若l1⊥l2,求a的值.
a=1
a=1或a=0
小试牛刀
点斜式
斜率和一点坐标
斜截式
斜率k和截距b
两点坐标
两点式
点斜式
两个截距
截距式
最后都要化成一般式Ax+By+C=0(A, B不同时为0)
课堂小结
