2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.3.2-2.3.3两点间的距离、点到直线的距离课件(25张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.3.2-2.3.3两点间的距离、点到直线的距离课件(25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 19:06:45 | ||
图片预览







文档简介
(共25张PPT)
2.3.2两点间的距离
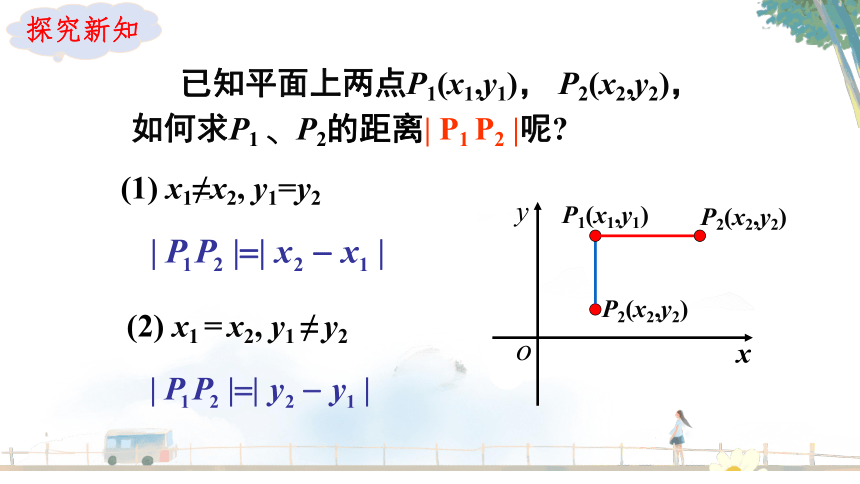
已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1 、P2的距离| P1 P2 |呢
(1) x1≠x2, y1=y2
(2) x1 = x2, y1 ≠ y2
P1(x1,y1)
P2(x2,y2)
x
y
o
P2(x2,y2)
探究新知
(3) x1 ≠ x2, y1 ≠ y2
2
2
|
|
y
x
OP
+
=
特别地, 原点O与任一点P(x, y)的距离:
x
O
y
探究新知
求下列两点间的距离:
(1) A(6,0),B(-2,0);
(2) C(0,-4),D(0,-1);
(3) P(6,0),Q(0,-2);
(4) M(2,1),N(5,-1).
|AB|=8
|CD|=3
|PQ|=
|MN|=
牛刀小试
2
2
)
1
(
4
|
|
2
=
+
+
=
a
PA
)
2
(
7
)
1
(
4
2
2
-
+
=
+
+
\
a
a
)
2
(
7
)
0
7
(
)
2
(
|
|
2
2
2
-
+
=
-
+
-
=
a
a
PB
1
=
a
解得:
)
1
(
4
)
0
2
(
)
1
(
|
|
2
2
2
+
+
=
-
+
-
-
=
a
a
PA
)
0
,
(
a
P
点的坐标为
解:设
|
|
|
|
=
PB
PA
Q
∴所求点P(1,0),且
典例分析
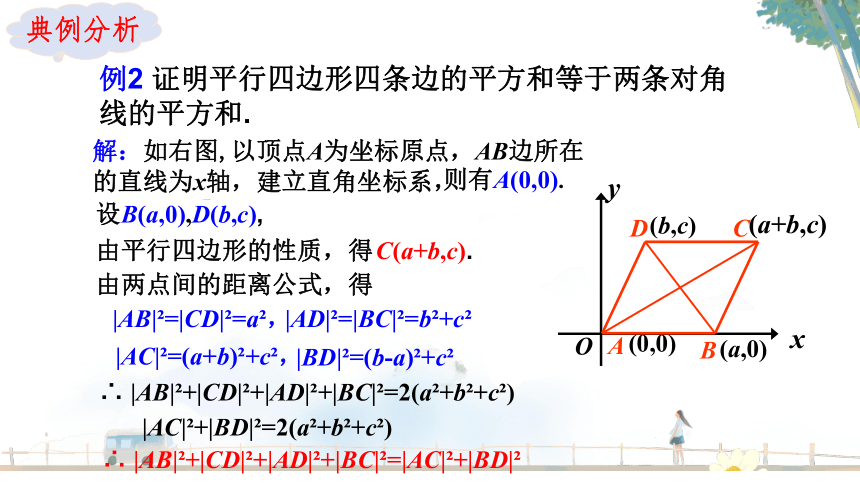
例2 证明平行四边形四条边的平方和等于两条对角线的平方和.
y
x
O
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
解:如右图,以顶点A为坐标原点,AB边所在的直线为x轴,建立直角坐标系,
则有A(0,0).
设B(a,0),D(b,c),
由平行四边形的性质,得
C(a+b,c).
典例分析
|AB| =|CD| =a ,
|AD| =|BC| =b +c
|AC| =(a+b) +c ,
由两点间的距离公式,得
|BD| =(b-a) +c
∴ |AB| +|CD| +|AD| +|BC| =2(a +b +c )
|AC| +|BD| =2(a +b +c )
∴ |AB| +|CD| +|AD| +|BC| =|AC| +|BD|
1.证明直角三角形斜边的中点到三个顶点的距离相等.
y
x
O
B
C
A
M
(0,0)
(a,0)
(0,b)
解:以顶点C为坐标原点,AC所在直线为x轴,建立直角坐标系,则有C(0,0)
巩固练习
故直角三角形斜边的中点到三个顶点的距离相等.
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算结果“翻译”所几何关系.
用坐标法解决简单的平面几何问题的步骤:
课堂小结
2.3.3点到直线的距离
x
y
P0 (x0,y0)
O
|y0|
|x0|
x0
y0
复习引入
点 到 x 轴, y 轴的距离?
x
y
P0 (x0,y0)
O
|x1-x0|
|y1-y0|
x0
y0
y1
x1
复习引入
点 到直线 x =x1, 直线 y =y1的距离?
已知点 ,直线 ,如何求点 到直线 的距离?
点 到直线 的距离,是指从点 到直线 的垂线段 的长度,其中 是垂足.
思考:如何求出 ?
x
y
O
探究新知
思路一:直接法
直线 的方程
直线 的斜率
直线 的方程
直线 的方程
交点
点 之间的距离 ( 到 的距离)
点 的坐标
直线 的斜率
点 的坐标
点 的坐标
两点间距离公式
x
y
O
思路简单运算繁琐
思路二:间接法
x
y
O
等面积法求出 |P0Q|
求出 |P0R|
求出|P0S|
利用勾股定理求出|RS|
S
R
求出点R的坐标
求出点S的坐标
思路三:向量投影法
求出直线l与y轴的交点M的坐标
x
y
O
M
求出P0M
求出直线l的垂直向量n
求出P0M在 n 上的投影|P0Q|
点 到直线 的距离:
x
y
O
探究新知
1.此公式是在A≠0、B≠0的前提下推导的;
2.如果A=0或B=0,此公式也成立;
3.用此公式时直线方程要先化成一般式.
注:
2.点(1,-1)到直线x-y+1=0的距离是( )
小试牛刀
×
C
牛刀小试
3.直线3x-4y-27=0上到点P(2,1)距离最近的点的坐标是 .
(5,-3)
例3 求点P(-1,2)到下列直线的距离:
①2x+y-10=0; ②3x=2.
解: ①根据点到直线的距离公式,得
②如图,直线3x=2平行于y轴,
O
y
x
l:3x=2
P(-1,2)
典例分析
2.求点B(1,-2)到直线4x+3y=0的距离.
1.求点A(-2,3)到直线3x+4y+3=0的距离.
4.求点P(-1,2)到直线3y=2的距离.
3.求点P(1,0)到直线3x+y-3=0的距离.
巩固练习
解:设边AB上的高为h, 则
x
y
O
-1
1
2
2
3
3
1
B (3,1)
A (1,3)
例4 已知点A(1,3), B(3,1), C(-1,0),求△ABC的面积.
典例分析
C (-1,0)
边AB所在直线l的方程为
即
点C(-1,0)到直线l的距离为
因此
巩固练习
1.已知点A(-1,3), B(-3,0), C(1,2),求△ABC的面积.
2. 已知直线l经过点M(-1,2),且A(2,3),B(-4,5)两点到直线l的距离相等,求直线l的方程.
解: 当过点M(-1,2)的直线l的斜率不存在时,直线l的方程为x=-1,
恰好A(2,3),B(-4,5)两点到直线l的距离相等,故x=-1满足题意;
当过点M(-1,2)的直线l的斜率存在时,
设l的方程为y-2=k(x+1),即kx-y+k+2=0,
由A(2,3)与B(-4,5)两点到直线l的距离相等,得
综上所述,直线l的方程为x=-1或x+3y-5=0.
跟踪训练
巩固练习
解:∵点A(1,1)与B(-3,1)到y轴的距离不相等,
∴直线l的斜率存在,设为k.
又直线l在y轴上的截距为2,则直线l的方程为y=kx+2,即kx-y+2=0.
由点A(1,1)与B(-3,1)到直线l的距离相等,
∴直线l的方程是y=2或x-y+2=0.
3.已知直线l经过点P(0,2),且A(1,1),B(-3,1)两点到直线l的距离相等,求直线l的方程.
巩固练习
另解:当直线l过线段AB的中点时,A,B两点到直线l的距离相等.
∵AB的中点是(-1,1),又直线l过点P(0,2),
∴直线l的方程是x-y+2=0.
当直线l∥AB时, A,B两点到直线l的距离相等.
∵直线AB的斜率为0,∴直线l的斜率为0,
∴直线l的方程为y=2.
综上所述,满足条件的直线l的方程是x-y+2=0或y=2.
巩固练习
3.已知直线l经过点P(0,2),且A(1,1),B(-3,1)两点到直线l的距离相等,求直线l的方程.
课堂小结
平面上两点P1(x1,y1), P2(x2,y2)的距离:
点 到直线 的距离:
2.3.2两点间的距离
已知平面上两点P1(x1,y1), P2(x2,y2),如何求P1 、P2的距离| P1 P2 |呢
(1) x1≠x2, y1=y2
(2) x1 = x2, y1 ≠ y2
P1(x1,y1)
P2(x2,y2)
x
y
o
P2(x2,y2)
探究新知
(3) x1 ≠ x2, y1 ≠ y2
2
2
|
|
y
x
OP
+
=
特别地, 原点O与任一点P(x, y)的距离:
x
O
y
探究新知
求下列两点间的距离:
(1) A(6,0),B(-2,0);
(2) C(0,-4),D(0,-1);
(3) P(6,0),Q(0,-2);
(4) M(2,1),N(5,-1).
|AB|=8
|CD|=3
|PQ|=
|MN|=
牛刀小试
2
2
)
1
(
4
|
|
2
=
+
+
=
a
PA
)
2
(
7
)
1
(
4
2
2
-
+
=
+
+
\
a
a
)
2
(
7
)
0
7
(
)
2
(
|
|
2
2
2
-
+
=
-
+
-
=
a
a
PB
1
=
a
解得:
)
1
(
4
)
0
2
(
)
1
(
|
|
2
2
2
+
+
=
-
+
-
-
=
a
a
PA
)
0
,
(
a
P
点的坐标为
解:设
|
|
|
|
=
PB
PA
Q
∴所求点P(1,0),且
典例分析
例2 证明平行四边形四条边的平方和等于两条对角线的平方和.
y
x
O
(b,c)
(a+b,c)
(a,0)
(0,0)
A
B
D
C
解:如右图,以顶点A为坐标原点,AB边所在的直线为x轴,建立直角坐标系,
则有A(0,0).
设B(a,0),D(b,c),
由平行四边形的性质,得
C(a+b,c).
典例分析
|AB| =|CD| =a ,
|AD| =|BC| =b +c
|AC| =(a+b) +c ,
由两点间的距离公式,得
|BD| =(b-a) +c
∴ |AB| +|CD| +|AD| +|BC| =2(a +b +c )
|AC| +|BD| =2(a +b +c )
∴ |AB| +|CD| +|AD| +|BC| =|AC| +|BD|
1.证明直角三角形斜边的中点到三个顶点的距离相等.
y
x
O
B
C
A
M
(0,0)
(a,0)
(0,b)
解:以顶点C为坐标原点,AC所在直线为x轴,建立直角坐标系,则有C(0,0)
巩固练习
故直角三角形斜边的中点到三个顶点的距离相等.
第一步:建立坐标系,用坐标表示有关的量;
第二步:进行有关的代数运算;
第三步:把代数运算结果“翻译”所几何关系.
用坐标法解决简单的平面几何问题的步骤:
课堂小结
2.3.3点到直线的距离
x
y
P0 (x0,y0)
O
|y0|
|x0|
x0
y0
复习引入
点 到 x 轴, y 轴的距离?
x
y
P0 (x0,y0)
O
|x1-x0|
|y1-y0|
x0
y0
y1
x1
复习引入
点 到直线 x =x1, 直线 y =y1的距离?
已知点 ,直线 ,如何求点 到直线 的距离?
点 到直线 的距离,是指从点 到直线 的垂线段 的长度,其中 是垂足.
思考:如何求出 ?
x
y
O
探究新知
思路一:直接法
直线 的方程
直线 的斜率
直线 的方程
直线 的方程
交点
点 之间的距离 ( 到 的距离)
点 的坐标
直线 的斜率
点 的坐标
点 的坐标
两点间距离公式
x
y
O
思路简单运算繁琐
思路二:间接法
x
y
O
等面积法求出 |P0Q|
求出 |P0R|
求出|P0S|
利用勾股定理求出|RS|
S
R
求出点R的坐标
求出点S的坐标
思路三:向量投影法
求出直线l与y轴的交点M的坐标
x
y
O
M
求出P0M
求出直线l的垂直向量n
求出P0M在 n 上的投影|P0Q|
点 到直线 的距离:
x
y
O
探究新知
1.此公式是在A≠0、B≠0的前提下推导的;
2.如果A=0或B=0,此公式也成立;
3.用此公式时直线方程要先化成一般式.
注:
2.点(1,-1)到直线x-y+1=0的距离是( )
小试牛刀
×
C
牛刀小试
3.直线3x-4y-27=0上到点P(2,1)距离最近的点的坐标是 .
(5,-3)
例3 求点P(-1,2)到下列直线的距离:
①2x+y-10=0; ②3x=2.
解: ①根据点到直线的距离公式,得
②如图,直线3x=2平行于y轴,
O
y
x
l:3x=2
P(-1,2)
典例分析
2.求点B(1,-2)到直线4x+3y=0的距离.
1.求点A(-2,3)到直线3x+4y+3=0的距离.
4.求点P(-1,2)到直线3y=2的距离.
3.求点P(1,0)到直线3x+y-3=0的距离.
巩固练习
解:设边AB上的高为h, 则
x
y
O
-1
1
2
2
3
3
1
B (3,1)
A (1,3)
例4 已知点A(1,3), B(3,1), C(-1,0),求△ABC的面积.
典例分析
C (-1,0)
边AB所在直线l的方程为
即
点C(-1,0)到直线l的距离为
因此
巩固练习
1.已知点A(-1,3), B(-3,0), C(1,2),求△ABC的面积.
2. 已知直线l经过点M(-1,2),且A(2,3),B(-4,5)两点到直线l的距离相等,求直线l的方程.
解: 当过点M(-1,2)的直线l的斜率不存在时,直线l的方程为x=-1,
恰好A(2,3),B(-4,5)两点到直线l的距离相等,故x=-1满足题意;
当过点M(-1,2)的直线l的斜率存在时,
设l的方程为y-2=k(x+1),即kx-y+k+2=0,
由A(2,3)与B(-4,5)两点到直线l的距离相等,得
综上所述,直线l的方程为x=-1或x+3y-5=0.
跟踪训练
巩固练习
解:∵点A(1,1)与B(-3,1)到y轴的距离不相等,
∴直线l的斜率存在,设为k.
又直线l在y轴上的截距为2,则直线l的方程为y=kx+2,即kx-y+2=0.
由点A(1,1)与B(-3,1)到直线l的距离相等,
∴直线l的方程是y=2或x-y+2=0.
3.已知直线l经过点P(0,2),且A(1,1),B(-3,1)两点到直线l的距离相等,求直线l的方程.
巩固练习
另解:当直线l过线段AB的中点时,A,B两点到直线l的距离相等.
∵AB的中点是(-1,1),又直线l过点P(0,2),
∴直线l的方程是x-y+2=0.
当直线l∥AB时, A,B两点到直线l的距离相等.
∵直线AB的斜率为0,∴直线l的斜率为0,
∴直线l的方程为y=2.
综上所述,满足条件的直线l的方程是x-y+2=0或y=2.
巩固练习
3.已知直线l经过点P(0,2),且A(1,1),B(-3,1)两点到直线l的距离相等,求直线l的方程.
课堂小结
平面上两点P1(x1,y1), P2(x2,y2)的距离:
点 到直线 的距离:
