2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.3.4 两条平行直线间的距离课件(11张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.3.4 两条平行直线间的距离课件(11张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 19:08:56 | ||
图片预览



文档简介
(共11张PPT)
2.3.4两条平行线间的距离
复习引入
1.两点P1(x1,y1), P2(x2,y2)两点间的距离公式:
2.点P0(x0, y0)到直线 的距离:
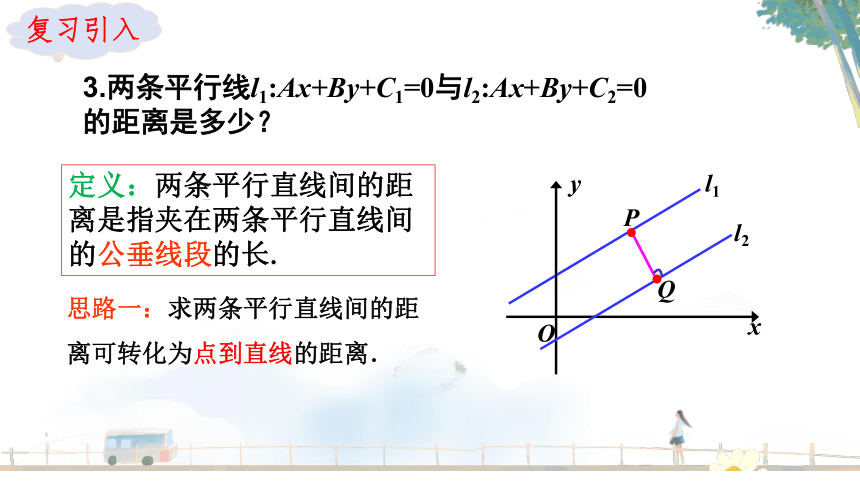
3.两条平行线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离是多少?
y
x
O
l2
l1
定义:两条平行直线间的距离是指夹在两条平行直线间的公垂线段的长.
Q
P
思路一:求两条平行直线间的距离可转化为点到直线的距离.
复习引入
3.两条平行线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离是多少?
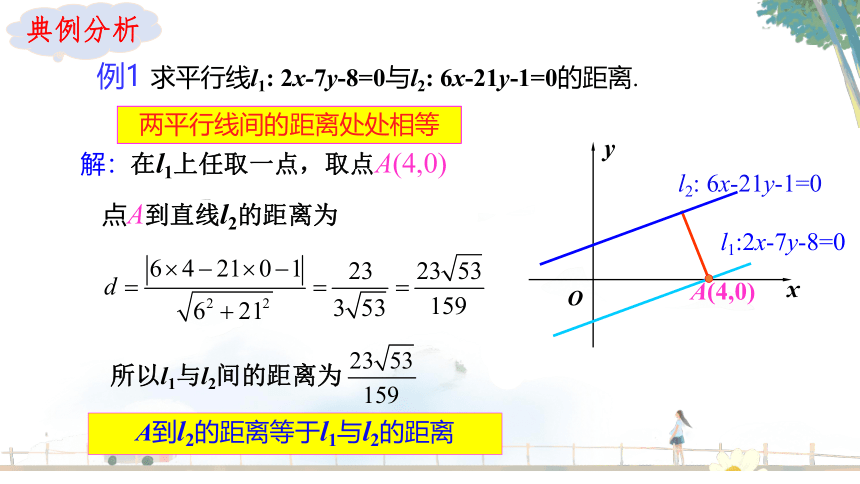
例1 求平行线l1: 2x-7y-8=0与l2: 6x-21y-1=0的距离.
解:在l1上任取一点,取点A(4,0)
A到l2的距离等于l1与l2的距离
y
O
x
l2: 6x-21y-1=0
l1:2x-7y-8=0
A(4,0)
两平行线间的距离处处相等
典例分析
点A到直线l2的距离为
所以l1与l2间的距离为
例2
证明:
典例分析
y
O
x
l1
l2
P
Q
y
O
x
l1
l2
P
Q
3.两条平行线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离是多少?
探究新知
注意:
2) 两直线方程中要求x,y的系数要相同.
1) 把直线方程要化成一般式;
例1 求平行线l1: 2x-7y-8=0与l2: 6x-21y-1=0的距离.
解:
y
O
x
l2: 6x-21y-1=0
l1:2x-7y-8=0
典例分析
直线l1: 2x-7y-8=0可化为6x-21y-24=0
由平行线间的距离公式,得
所以l1与l2间的距离为
典例分析
1.平行线2x+3y-8=0和2x+3y+18=0的距离是______;
2.两平行线3x+4y=10和6x+8y=0的距离是____.
3.两平行线3x-2y-1=0和6x-4y+2=0的距离是_______.
2
巩固练习
例3 求与直线l:5x-12y+6=0平行,且到l得距离为2的直线的方程.
解:设所求直线为5x-12y+C=0,
所求直线为5x-12y-20=0或5x-12+32=0.
即|6-C|=26,解得C=-20或32.
典例分析
典例分析
例4 过点P(1,2),且与点A(2,3)和B(4,-5)距离相等的直线 l 的方程。
①当直线平行于直线AB时,所求直线的斜率为:
故直线方程为y-2=-4(x-1)即4x+y-6=0
解:
②当直线过AB的中点(3,-1)时斜率为:
故直线方程为y-2= (x-1),即3x+2y-7=0;
所以求直线方程是为:4x+y-6=0或3x+2y-7=0.
课堂小结
1.两点P1(x1,y1), P2(x2,y2)两点间的距离公式:
2.点P0(x0, y0)到直线 的距离:
3.两条平行线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离:
2.3.4两条平行线间的距离
复习引入
1.两点P1(x1,y1), P2(x2,y2)两点间的距离公式:
2.点P0(x0, y0)到直线 的距离:
3.两条平行线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离是多少?
y
x
O
l2
l1
定义:两条平行直线间的距离是指夹在两条平行直线间的公垂线段的长.
Q
P
思路一:求两条平行直线间的距离可转化为点到直线的距离.
复习引入
3.两条平行线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离是多少?
例1 求平行线l1: 2x-7y-8=0与l2: 6x-21y-1=0的距离.
解:在l1上任取一点,取点A(4,0)
A到l2的距离等于l1与l2的距离
y
O
x
l2: 6x-21y-1=0
l1:2x-7y-8=0
A(4,0)
两平行线间的距离处处相等
典例分析
点A到直线l2的距离为
所以l1与l2间的距离为
例2
证明:
典例分析
y
O
x
l1
l2
P
Q
y
O
x
l1
l2
P
Q
3.两条平行线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离是多少?
探究新知
注意:
2) 两直线方程中要求x,y的系数要相同.
1) 把直线方程要化成一般式;
例1 求平行线l1: 2x-7y-8=0与l2: 6x-21y-1=0的距离.
解:
y
O
x
l2: 6x-21y-1=0
l1:2x-7y-8=0
典例分析
直线l1: 2x-7y-8=0可化为6x-21y-24=0
由平行线间的距离公式,得
所以l1与l2间的距离为
典例分析
1.平行线2x+3y-8=0和2x+3y+18=0的距离是______;
2.两平行线3x+4y=10和6x+8y=0的距离是____.
3.两平行线3x-2y-1=0和6x-4y+2=0的距离是_______.
2
巩固练习
例3 求与直线l:5x-12y+6=0平行,且到l得距离为2的直线的方程.
解:设所求直线为5x-12y+C=0,
所求直线为5x-12y-20=0或5x-12+32=0.
即|6-C|=26,解得C=-20或32.
典例分析
典例分析
例4 过点P(1,2),且与点A(2,3)和B(4,-5)距离相等的直线 l 的方程。
①当直线平行于直线AB时,所求直线的斜率为:
故直线方程为y-2=-4(x-1)即4x+y-6=0
解:
②当直线过AB的中点(3,-1)时斜率为:
故直线方程为y-2= (x-1),即3x+2y-7=0;
所以求直线方程是为:4x+y-6=0或3x+2y-7=0.
课堂小结
1.两点P1(x1,y1), P2(x2,y2)两点间的距离公式:
2.点P0(x0, y0)到直线 的距离:
3.两条平行线l1:Ax+By+C1=0与l2:Ax+By+C2=0的距离:
