2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.4.1 圆的标准方程课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.4.1 圆的标准方程课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:13:47 | ||
图片预览







文档简介
(共20张PPT)
2.4.1 圆的标准方程
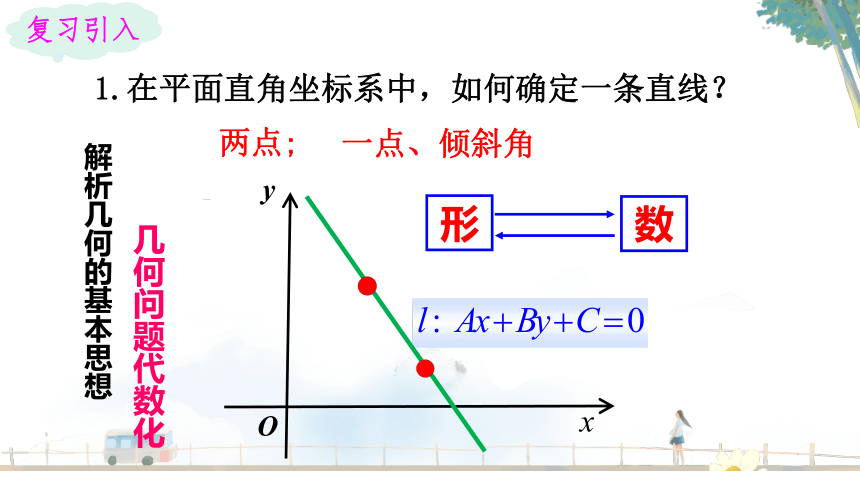
1.在平面直角坐标系中,如何确定一条直线?
两点;
一点、倾斜角
复习引入
y
O
x
形
数
解析几何的基本思想
几何问题代数化
欣赏生活中美丽的圆
欣赏生活中美丽的圆
欣赏生活中美丽的圆
车行天下
赵州桥----国际土木工程历史古迹
欣赏生活中美丽的圆
毕达哥拉斯学派
一切空间图形中,
球形是最美的图形.
一切平面图形中,
圆形是最美的图形.
圆
圆心、半径
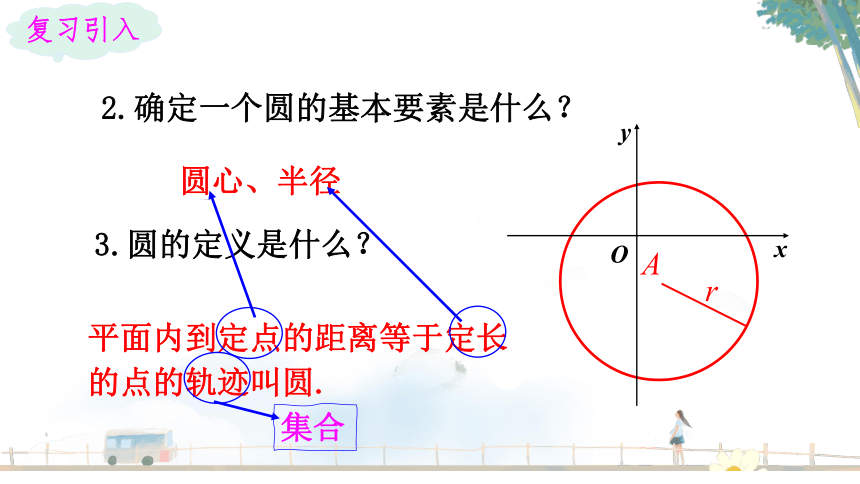
2.确定一个圆的基本要素是什么?
3.圆的定义是什么?
平面内到定点的距离等于定长的点的轨迹叫圆.
复习引入
A
r
x
y
O
集合
根据两点间距离公式,即
_________________
在平面直角坐标系中,如何确定圆的方程呢?
两边平方,得
____________________
|MC|与r的关系:_______
|MC|=r
M(x, y)
C(a,b)
设圆心C(a,b)和圆上动点M(x,y),半径为r.
探究新知
x
y
O
1.括号内x,y的系数都为______
2.括号内连接符号为____,括号外连接符号为___
特点:
特别:
圆的标准方程
(x- ) 2 + (y- ) 2 = r2
>0
3.圆上点_______;圆心_______;半径_____
1
-
+
当圆心在原点(0,0)上时,圆的方程为:
>0
探究新知
1.判断下列方程是圆的方程吗?
小试牛刀
2.根据圆的标准方程,求出圆心和半径.
(1)圆
的圆心是______,半径是___
(2)圆
的圆心是______,半径是____
(3)圆
的圆心是_____,半径是____
(3, 4)
(-3, 1)
3.已知圆心和半径,写出圆的标准方程
(1)圆心为(1, 2),半径为2,___________________
(2)圆心为(-1, 2),半径为1,__________________
(3)圆心为(1, -2),半径为 , ____________________
小试牛刀
例1 写出圆心为A(2, -3),半径长等于5的圆的方程,并判断点M1(5, -7) , M2(-2, -1) 是否在这个圆上.
解: 圆心是A(2, -3), 半径长等于5的圆的标准方程是:
把M1(5, -7)的坐标代入方程
左右两边相等,点M1的坐标适合圆的方程,所以点
M1在这个圆上;
典例分析
把点M2(-2, -1)的坐标代入方程
的左边,得 ,左右两边不相等,点M2的坐标不适合圆的方程,所以点M2不在这个圆上.
探究:如何确定点P(x0, y0)与圆 的位置关系?
|PC||PC|=r
|PC|>r
点在圆上
点在圆外
点在圆内
位置关系
图形
几何条件
代数形式
点与圆的位置关系
C
P
C
C
P
P
探究新知
A.在圆外 B.在圆上
C.在圆内 D.在圆上或圆外
(1)点P(3,2)与圆(x-2)2+(y-3)2=4的位置关系( )
C
(2)点P(m,5)与圆x2+y2=25的位置关系( )
D
A.在圆外 B.在圆上
C.在圆内 D.在圆上或圆外
4.判断点与圆的位置关系
小试牛刀
A.-4C.-5(3)已知点P(a,a+1)在圆x2+y2=25的内部,则a的取值范围是( )
A
解:设所求圆的方程为:
因为A(5,1), B(7,-3),C(2,-8)都在圆上,所以有
所求圆的方程为:
例2 △ABC的三个顶点的坐标分别是A(5,1), B(7,-3),C(2,-8), 求它的外接圆的方程.
典例分析
解得
解法1:
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
典例分析
设圆C的方程为
∵圆心在直线 l: x-y+1=0上,且圆经过A(1,1),B(2,-2)
解法2:
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
典例分析
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
典例分析
解法3: ∵ A(1,1),B(2,-2)
∴圆心C(-3,-2)
1.根据下列条件,求圆的方程:
(1)求过两点A(0,4)和B(4,6), 且圆心在直线x-y+1=0上的圆的标准方程.
(2)圆心在直线5x-3y=8上, 又与两坐标轴相切,求圆的方程.
巩固练习
圆的标准方程
圆心、半径
点与圆的位置关系
圆外:
圆上:
圆内:
通过今天的学习,你学到了哪些新知识?
在今天的学习中,运用了什么数学方法与思想?
类比法、坐标法、代数法、数形结合等
圆的基本要素
课堂小结
2.4.1 圆的标准方程
1.在平面直角坐标系中,如何确定一条直线?
两点;
一点、倾斜角
复习引入
y
O
x
形
数
解析几何的基本思想
几何问题代数化
欣赏生活中美丽的圆
欣赏生活中美丽的圆
欣赏生活中美丽的圆
车行天下
赵州桥----国际土木工程历史古迹
欣赏生活中美丽的圆
毕达哥拉斯学派
一切空间图形中,
球形是最美的图形.
一切平面图形中,
圆形是最美的图形.
圆
圆心、半径
2.确定一个圆的基本要素是什么?
3.圆的定义是什么?
平面内到定点的距离等于定长的点的轨迹叫圆.
复习引入
A
r
x
y
O
集合
根据两点间距离公式,即
_________________
在平面直角坐标系中,如何确定圆的方程呢?
两边平方,得
____________________
|MC|与r的关系:_______
|MC|=r
M(x, y)
C(a,b)
设圆心C(a,b)和圆上动点M(x,y),半径为r.
探究新知
x
y
O
1.括号内x,y的系数都为______
2.括号内连接符号为____,括号外连接符号为___
特点:
特别:
圆的标准方程
(x- ) 2 + (y- ) 2 = r2
>0
3.圆上点_______;圆心_______;半径_____
1
-
+
当圆心在原点(0,0)上时,圆的方程为:
>0
探究新知
1.判断下列方程是圆的方程吗?
小试牛刀
2.根据圆的标准方程,求出圆心和半径.
(1)圆
的圆心是______,半径是___
(2)圆
的圆心是______,半径是____
(3)圆
的圆心是_____,半径是____
(3, 4)
(-3, 1)
3.已知圆心和半径,写出圆的标准方程
(1)圆心为(1, 2),半径为2,___________________
(2)圆心为(-1, 2),半径为1,__________________
(3)圆心为(1, -2),半径为 , ____________________
小试牛刀
例1 写出圆心为A(2, -3),半径长等于5的圆的方程,并判断点M1(5, -7) , M2(-2, -1) 是否在这个圆上.
解: 圆心是A(2, -3), 半径长等于5的圆的标准方程是:
把M1(5, -7)的坐标代入方程
左右两边相等,点M1的坐标适合圆的方程,所以点
M1在这个圆上;
典例分析
把点M2(-2, -1)的坐标代入方程
的左边,得 ,左右两边不相等,点M2的坐标不适合圆的方程,所以点M2不在这个圆上.
探究:如何确定点P(x0, y0)与圆 的位置关系?
|PC|
|PC|>r
点在圆上
点在圆外
点在圆内
位置关系
图形
几何条件
代数形式
点与圆的位置关系
C
P
C
C
P
P
探究新知
A.在圆外 B.在圆上
C.在圆内 D.在圆上或圆外
(1)点P(3,2)与圆(x-2)2+(y-3)2=4的位置关系( )
C
(2)点P(m,5)与圆x2+y2=25的位置关系( )
D
A.在圆外 B.在圆上
C.在圆内 D.在圆上或圆外
4.判断点与圆的位置关系
小试牛刀
A.-4
A
解:设所求圆的方程为:
因为A(5,1), B(7,-3),C(2,-8)都在圆上,所以有
所求圆的方程为:
例2 △ABC的三个顶点的坐标分别是A(5,1), B(7,-3),C(2,-8), 求它的外接圆的方程.
典例分析
解得
解法1:
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
典例分析
设圆C的方程为
∵圆心在直线 l: x-y+1=0上,且圆经过A(1,1),B(2,-2)
解法2:
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
典例分析
例3 己知圆心为C的圆经过点A(1,1),B(2,-2)两点, 且圆心C在直线 l: x-y+1=0上, 求此圆的标准方程.
典例分析
解法3: ∵ A(1,1),B(2,-2)
∴圆心C(-3,-2)
1.根据下列条件,求圆的方程:
(1)求过两点A(0,4)和B(4,6), 且圆心在直线x-y+1=0上的圆的标准方程.
(2)圆心在直线5x-3y=8上, 又与两坐标轴相切,求圆的方程.
巩固练习
圆的标准方程
圆心、半径
点与圆的位置关系
圆外:
圆上:
圆内:
通过今天的学习,你学到了哪些新知识?
在今天的学习中,运用了什么数学方法与思想?
类比法、坐标法、代数法、数形结合等
圆的基本要素
课堂小结
