2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.5.1 直线与圆的位置关系(2)课件(13张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册2.5.1 直线与圆的位置关系(2)课件(13张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 09:19:11 | ||
图片预览




文档简介
(共13张PPT)
2.5.1 直线与圆的位置关系
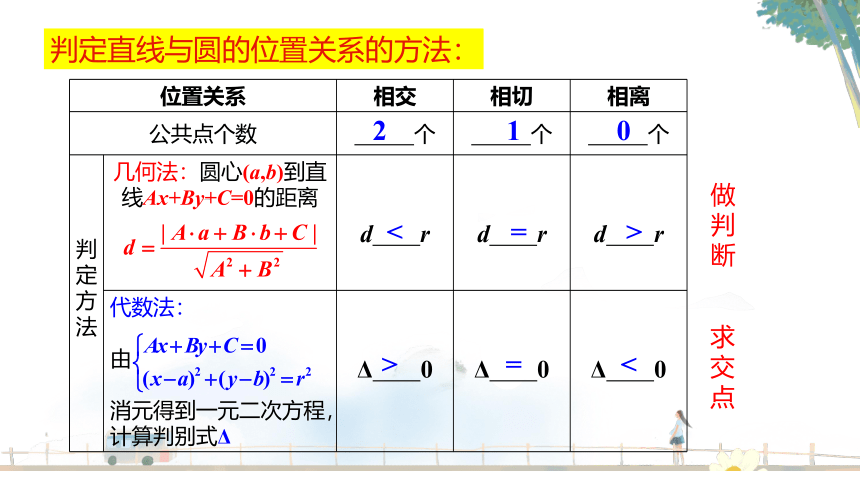
位置关系 相交 相切 相离
公共点个数 个 个 个
判定方法 几何法:圆心(a,b)到直线Ax+By+C=0的距离 d r d r
d r
代数法: 由 消元得到一元二次方程,计算判别式Δ Δ 0 Δ 0
Δ 0
判定直线与圆的位置关系的方法:
2
1
0
<
=
>
>
=
<
做判断
求交点
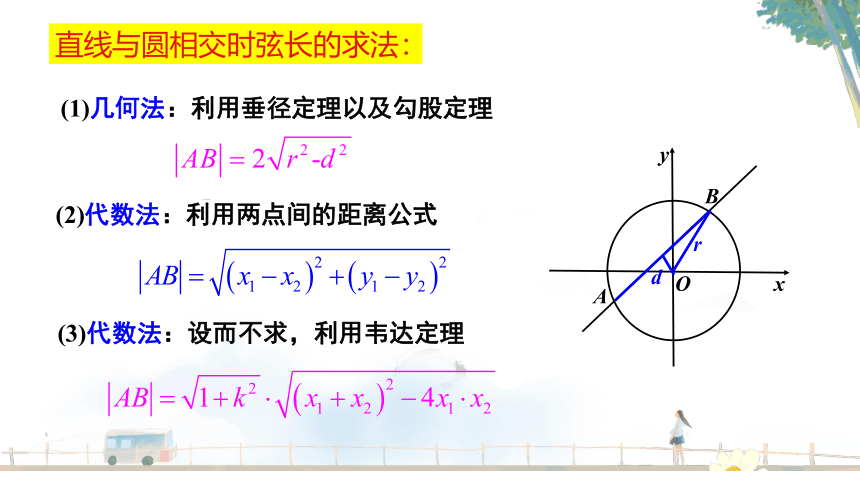
AD
x
y
O
A
B
d
r
(3)代数法:设而不求,利用韦达定理
(1)几何法:利用垂径定理以及勾股定理
(2)代数法:利用两点间的距离公式
直线与圆相交时弦长的求法:
2.已知直线 被圆 截得的弦长为 ,点(m,n) 是直线l上的任意一点,则m2+n2的最小值为( )
A.1 B.2 C.3 D.4
A
D.-2
3.若直线 被圆 所截弦长最短,则m=( )
A.4 B.2 C. D.-2
C
1. 直线2x-y+2=0 和圆(x-1)2+ (y-2)2 =4相交,直线被圆截得的弦长为 .
4.已知圆C: x2+y2- 2x-4y-20=0. 过点P(4,-4)的直线l被圆C截得的弦长为8,求直线l的方程.
设点C到直线l 距离为d,则
由圆的弦长公式,得 ,解得d=3
此时直线的方程为3x+4y+4=0
综上,直线方程为x=4或3x+4y+4=0.
解得
①当直线l斜率不存在时,直线方程为x=4,满足题意
②当直线l斜率存在时,设直线方程为y+4=k(x-4),即kx-y-4k-4=0
解: 圆C: x2+y2- 2x-4y-20=0可化为(x-1)2+ (y-2)2 =25,则
圆心坐标为C(1,2) ,半径为r=5
做这种题要分类讨论:(答题模板)
①当直线斜率不存在时,直线方程为x=x0
②当直线斜率存在时,设直线方程为
y-y0=k(x-x0).
由
5.已知圆C: x2+y2- 2x-4y-20=0. 当k取何值时,直线kx-y+3k +1=0与圆C相交的弦长最短,并求出最短弦长.
由直线kx-y+3k +1=0可化为y-1=k(x+3),
可得直线l过定点M(-3,1),
当CM⊥l 时,弦长最短,
此时最短弦长为
又由 , 可得k=-4
解: 圆C: x2+y2- 2x-4y-20=0可化为(x-1)2+ (y-2)2 =25,则
圆心坐标为C(1,2) ,半径为r=5
1.点P在圆上时:
求过圆上一点(x0, y0)的切线方程:
①先求切点与圆心连线的斜率k,
②再由垂直关系得切线的斜率为 ,
③由点斜式可得切线方程
如果斜率为零或不存在,则由图形可直接得切线方程 y=y0或 x=x0.
求过一点P的圆的切线方程的方法:
1.设点M(x0,y0)为圆 x2+y2=r2上一点,则过M 点可以作几条圆的切线?如何求过点M 的圆的切线方程?
x
O
y
过圆上一点的切线方程为x0x+y0y=r2
M(x0,y0)
2.点P在圆外时:
求过圆外一点(x0, y0)的切线方程:
(1)几何法: 设切线方程为y-y0=k(x-x0),由圆心到直线的距离等于半径,即d=r,可求得k,也就是切线方程.
(2)代数法: 设切线方程为y-y0=k(x-x0),与圆的方程联立,消去y后得到关于x的一元二次方程,由△=0求出k,可得切线方程.
做这种题要分类讨论:(答题模板)
①当切线斜率不存在时,切线方程为x=x0;
②当切线斜率存在时,设切线方程为y-y0=k(x-x0).
求过一点P的圆的切线方程的方法:
若通过上述方法只求出一个斜率k, 则说明另一条切线的斜率不存在, 此时另一条切线方程为x=x0.
2.过点P(1,2)作圆O: x2+y2=1的切线l, 求此切线l的方程.
O
P
y
x
解:
即kx-y+2-k=0
由圆心(0,0)到切线l的距离等于圆的半径1,得
设切线l的方程为y-2=k(x-1),
②当切线l的斜率存在时,
此时切线l的方程为3x-4y+5=0.
①当切线l的斜率不存在时,
解得
此时切线l的方程为x=1
综上所述,切线l的方程为x=1或3x-4y+5=0.
2.5.1 直线与圆的位置关系
位置关系 相交 相切 相离
公共点个数 个 个 个
判定方法 几何法:圆心(a,b)到直线Ax+By+C=0的距离 d r d r
d r
代数法: 由 消元得到一元二次方程,计算判别式Δ Δ 0 Δ 0
Δ 0
判定直线与圆的位置关系的方法:
2
1
0
<
=
>
>
=
<
做判断
求交点
AD
x
y
O
A
B
d
r
(3)代数法:设而不求,利用韦达定理
(1)几何法:利用垂径定理以及勾股定理
(2)代数法:利用两点间的距离公式
直线与圆相交时弦长的求法:
2.已知直线 被圆 截得的弦长为 ,点(m,n) 是直线l上的任意一点,则m2+n2的最小值为( )
A.1 B.2 C.3 D.4
A
D.-2
3.若直线 被圆 所截弦长最短,则m=( )
A.4 B.2 C. D.-2
C
1. 直线2x-y+2=0 和圆(x-1)2+ (y-2)2 =4相交,直线被圆截得的弦长为 .
4.已知圆C: x2+y2- 2x-4y-20=0. 过点P(4,-4)的直线l被圆C截得的弦长为8,求直线l的方程.
设点C到直线l 距离为d,则
由圆的弦长公式,得 ,解得d=3
此时直线的方程为3x+4y+4=0
综上,直线方程为x=4或3x+4y+4=0.
解得
①当直线l斜率不存在时,直线方程为x=4,满足题意
②当直线l斜率存在时,设直线方程为y+4=k(x-4),即kx-y-4k-4=0
解: 圆C: x2+y2- 2x-4y-20=0可化为(x-1)2+ (y-2)2 =25,则
圆心坐标为C(1,2) ,半径为r=5
做这种题要分类讨论:(答题模板)
①当直线斜率不存在时,直线方程为x=x0
②当直线斜率存在时,设直线方程为
y-y0=k(x-x0).
由
5.已知圆C: x2+y2- 2x-4y-20=0. 当k取何值时,直线kx-y+3k +1=0与圆C相交的弦长最短,并求出最短弦长.
由直线kx-y+3k +1=0可化为y-1=k(x+3),
可得直线l过定点M(-3,1),
当CM⊥l 时,弦长最短,
此时最短弦长为
又由 , 可得k=-4
解: 圆C: x2+y2- 2x-4y-20=0可化为(x-1)2+ (y-2)2 =25,则
圆心坐标为C(1,2) ,半径为r=5
1.点P在圆上时:
求过圆上一点(x0, y0)的切线方程:
①先求切点与圆心连线的斜率k,
②再由垂直关系得切线的斜率为 ,
③由点斜式可得切线方程
如果斜率为零或不存在,则由图形可直接得切线方程 y=y0或 x=x0.
求过一点P的圆的切线方程的方法:
1.设点M(x0,y0)为圆 x2+y2=r2上一点,则过M 点可以作几条圆的切线?如何求过点M 的圆的切线方程?
x
O
y
过圆上一点的切线方程为x0x+y0y=r2
M(x0,y0)
2.点P在圆外时:
求过圆外一点(x0, y0)的切线方程:
(1)几何法: 设切线方程为y-y0=k(x-x0),由圆心到直线的距离等于半径,即d=r,可求得k,也就是切线方程.
(2)代数法: 设切线方程为y-y0=k(x-x0),与圆的方程联立,消去y后得到关于x的一元二次方程,由△=0求出k,可得切线方程.
做这种题要分类讨论:(答题模板)
①当切线斜率不存在时,切线方程为x=x0;
②当切线斜率存在时,设切线方程为y-y0=k(x-x0).
求过一点P的圆的切线方程的方法:
若通过上述方法只求出一个斜率k, 则说明另一条切线的斜率不存在, 此时另一条切线方程为x=x0.
2.过点P(1,2)作圆O: x2+y2=1的切线l, 求此切线l的方程.
O
P
y
x
解:
即kx-y+2-k=0
由圆心(0,0)到切线l的距离等于圆的半径1,得
设切线l的方程为y-2=k(x-1),
②当切线l的斜率存在时,
此时切线l的方程为3x-4y+5=0.
①当切线l的斜率不存在时,
解得
此时切线l的方程为x=1
综上所述,切线l的方程为x=1或3x-4y+5=0.
