2021-2022学年高一数学人教A版(2019)必修一4.5.3函数模型的应用课件(共30张PPT)
文档属性
| 名称 | 2021-2022学年高一数学人教A版(2019)必修一4.5.3函数模型的应用课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 389.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:16:51 | ||
图片预览








文档简介
(共30张PPT)
4.5.3 函数模型的应用
我们知道,函数是描述客观世界变化规律的数学模型,不同的变化规律需要用不同的函数模型来刻画.面临一个实际问题,该如何选择恰当的函数模型来刻画它呢?
温故知新
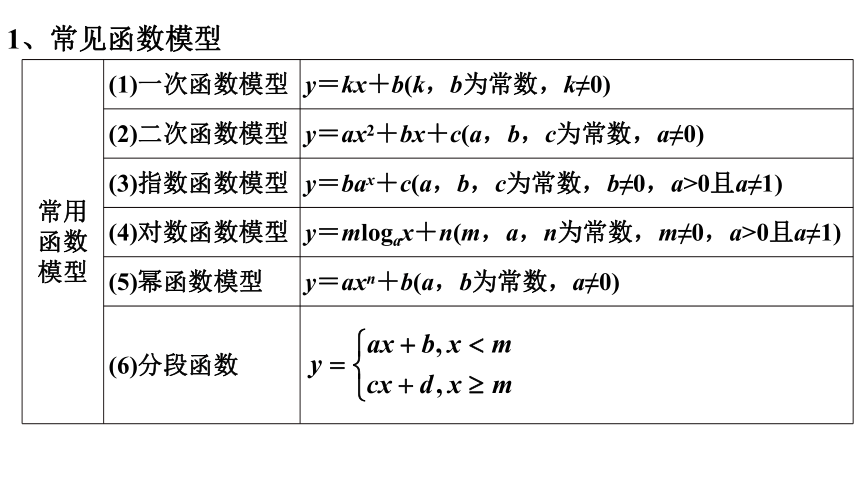
1、常见函数模型
常用函数模型 (1)一次函数模型 y=kx+b(k,b为常数,k≠0)
(2)二次函数模型 y=ax2+bx+c(a,b,c为常数,a≠0)
(3)指数函数模型 y=bax+c(a,b,c为常数,b≠0,a>0且a≠1)
(4)对数函数模型 y=mlogax+n(m,a,n为常数,m≠0,a>0且a≠1)
(5)幂函数模型 y=axn+b(a,b为常数,a≠0)
(6)分段函数
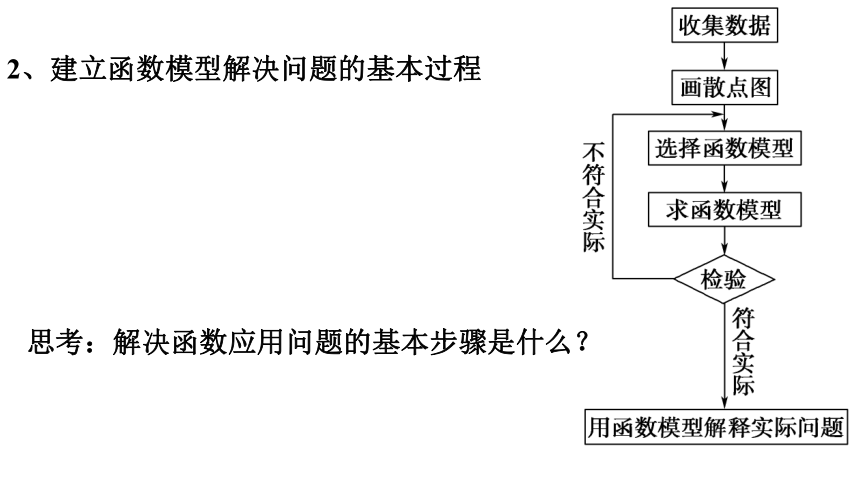
2、建立函数模型解决问题的基本过程
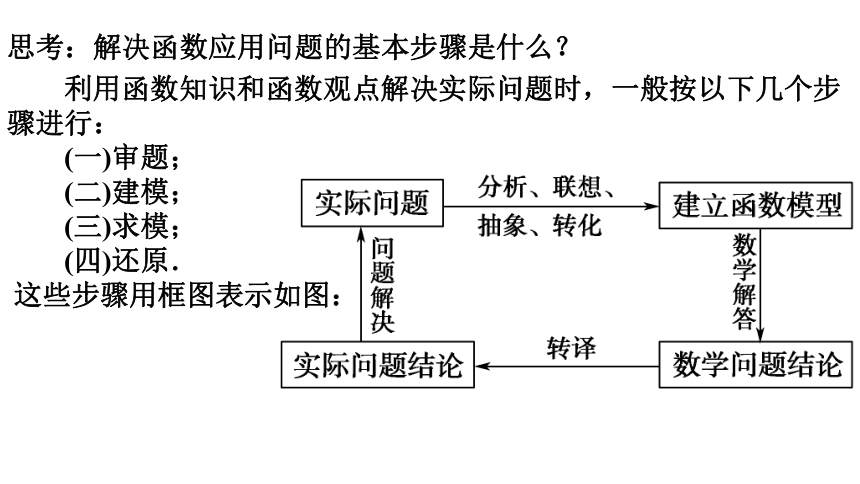
思考:解决函数应用问题的基本步骤是什么?
利用函数知识和函数观点解决实际问题时,一般按以下几个步骤进行:
(一)审题;
(二)建模;
(三)求模;
(四)还原.
这些步骤用框图表示如图:
思考:解决函数应用问题的基本步骤是什么?
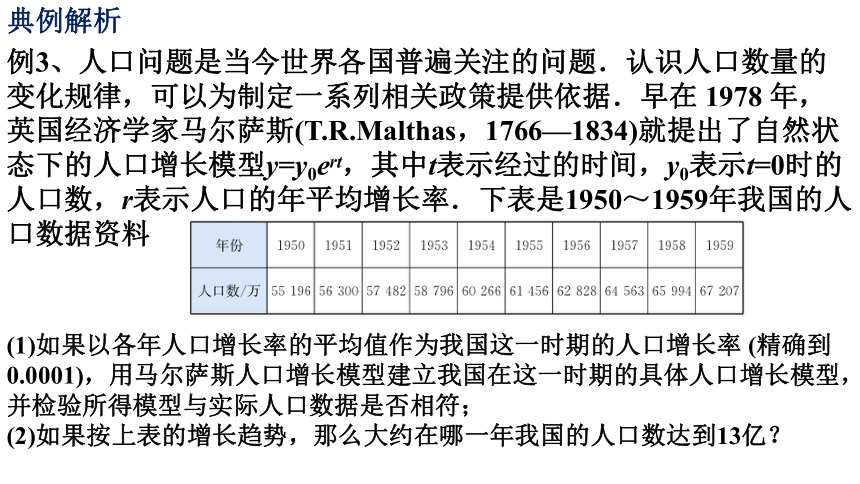
例3、人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为制定一系列相关政策提供依据.早在 1978 年,英国经济学家马尔萨斯(T.R.Malthas,1766—1834)就提出了自然状态下的人口增长模型y=y0ert,其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的年平均增长率.下表是1950~1959年我国的人口数据资料
(1)如果以各年人口增长率的平均值作为我国这一时期的人口增长率 (精确到0.0001),用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;
(2)如果按上表的增长趋势,那么大约在哪一年我国的人口数达到13亿?
典例解析
分析:用马尔萨斯人口增长模型建立具体人口增长模型,就是要确定其中的初始量y0和年平均增长率r.
解:(1)设1951~1959年我国各年的人口增长率分别为r1,r2,…,r9.
由55196(1+r1)=56300可得1951年的人口增长率r1≈0.0200.
同理可得,r2≈0.0210,r3≈0.0229,r4≈0.0250,r5≈0.0197,
r6≈0.0223,r7≈0.0276,r8≈0.0222,r9≈0.0154.
于是,1951~1959年期间,
我国人口的年平均增长率为:
r=(r1+r2+…+r9)÷9≈0.0221
令y0=55196,
则我国在1950~1959年期间的人口增长模型为y=55196e0.0221t,t∈N.
根据表中的数据画出散点图,并画出函数y=55196e0.0221t(t∈N)的图象,由图可以看出,所得模型与1950~1959年的实际人口数据基本吻合 .
事实上,我国1989年的人口数为11.27亿,直到2005年才突破13亿.对由函数模型所得的结果与实际情况不符 , 你有何看法 ?
因为人口基数较大,人口增长过快,与我国经济发展水平产生了较大矛盾,所以我国从20世纪70年代逐步实施了计划生育政策.因此这一阶段的人口增长条件并不符合马尔萨斯人口增长模型的条件,自然就出现了依模型得到的结果与实际不符的情况.
(2)如果按上表的增长趋势,那么大约在t=39,即1989年我国的人口数达到13亿.
例4、2010年,考古学家对良渚古城水利系统中一条水坝的建筑材料上提取的草茎遗存进行碳14年代学检测,检测出碳 14的残留量约为初始量的55.2%,能否以此推断此水坝大概是什么年代建成的
分析:因为死亡生物机体内碳14的初始量按确定的衰减率衰减,属于指数衰减,所以应选择函数y=kax(k∈R,且k≠0;a>0,且a≠1)建立数学模型.
解:设样本中碳14的初始量为k,衰减率为p(0y=k(1-p)x(k∈R,且k≠0;0由碳14的半衰期为5730年,得
典例解析
于是 ,所以
由样本中碳14 的残余量约为初始量的55.2%可知 ,即
解得 .由计算工具得x≈4912.
因为2010年之前的4912年是公元前2902年,所以推断此水坝大概是公元前2902年建成的.
归纳总结
[规律方法]已知函数模型解决实际问题,往往给出的函数解析式含有参数,需要将题中的数据代入函数模型,求得函数模型中的参数,再将问题转化为已知函数解析式求函数值或自变量的值.
例5、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?
①问题中涉及哪些数量关系?
②如何用函数描述这些数量关系?
投资天数、回报金额
日回报
累计回报
典例解析
40
40
40
40
40
10
10+10
=10×2
10+10+10
=10×3
10+10+10+10
=10×4
10+10+10+10+10
=10×5
0.4
0.4×2
0.4×2×2
=0.4×22
0.4×2×2×2
=0.4×23
0.4×2×2×2×2
=0.4×24
方案一
方案二
方案三
1
2
3
4
5
则方案一可以用函数________________进行描述;
方案二可以用函数__________________进行描述;
方案三可以用函数___________________进行描述。
设第x天的回报是y元,
y=40 (x∈N*)
y=10x (x∈N*)
y=0.4×2x-1 (x∈N*)
三种方案每天回报表
x/天 方案1 方案2 方案3 y/元 增加量/元 y/元 增加量/元 y/元 增加量/元
1 40 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
10 40 0 100 10 204.8 102.4
… … … … … … …
30 40 0 300 10 214748365 107374182.4
0
x
y
20
40
60
80
100
120
140
4
2
6
8
10
12
1 2 3 4 5 6 7 8 9 10 11 … 30
方案一 40 80 120 160 200 240 280 320 360 400 440 … 1200
方案二 10 30 60 100 150 210 280 360 450 550 660 … 4650
方案三 0 1 2.8 6 12 25 50.8 102 204 409 819 … 429496729.2
例5 累计回报表
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三。
假如某公司每天给你投资1万元,共投资30天。公司要求你给他的回报是:第一天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天,你认为这样的交易对你有利吗?
你30天内给公司的回报为:
0.01+0.01×2+0.01×22+…+0.01×229
=10737418.23
≈1074(万元)
30万元
解答如下:公司30天内为你的总投资为:
上述例子只是一种假想情况,但从中可以看到,不同的函数增长模型,增长变化存在很大差异
一次函数,
对数型函数,
指数函数。
①例6涉及了哪几类函数模型?
②你能用数学语言描述符合公司奖励方案的条件吗
例6、某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%。
现有三个奖励模型:y=0.25x, y=log7x+1, y=1.002x,其中哪个模型能符合公司的要求?
典例解析
分析:本例提供了三个不同增长方式的奖励模型,按要求选择其中一个函数作为刻画奖金总数与销售利润的关系.由于公司总的利润目标为1000万元,所以销售人员的销售利润一般不会超过公司总的利润.于是,只需在区间[10,1000]上,寻找并验证所选函数是否满足两条要求 :
第一,奖金总数不超过5万元,即最大值不大于5;
第二,奖金不超过利润的25%,即y≤0.25x.不妨先画出函数图象,通过观察函数图象,得到初步的结论,再通过具体计算,确认结果.
解:借助信息技术画出函数y=5,y=0.25x,y=log7x+1,y=1.002x的图象. 观察图象发现,在区间[10,1000]上 , 模型y=0.25x,y=1.002x的图象都有一部分在直线y=5的上方 , 只有模型y=log7x+1的图象始终在y=5的下方 , 这说明只有按模型y=log7x+1进行奖励时才符合公司的要求 .
下面通过计算确认上述判断 .
先计算哪个模型的奖金总数不超过5万元 .
对于模型y=0.25x, 它在区间[10,1000]上单调递增 , 而且当x=20时,y=5,
因此,当x>20时,y>5,所以该模型不符合要求 ;
对于模型y=1.002x,由函数图象,并利用信息技术,可知在区间(805,806)内有一个点x0满足1.002x0=5,由于它在区间[10,1000]上单调递增,因此当x>x0时,y>5,所以该模型也不符合要求 ;
对于模型y=log7x+1,它在区间[10,1000]上单调递增,而且当x=1000 时 ,y=log71000+1≈4.55<5 , 所以它符合奖金总数不超过5万元的要求 .
再计算按模型y=log7x+1奖励时, 奖金是否不超过利润的25% ,即当x∈[10,1000]时,是否有y≤0.25x,
即y=log7x+1≤0.25x成立 .
令f(x)=log7x+1-0.25x,x∈[10,1000],
利用信息技术画出它的图象
由图象可知函数f(x)在区间[10,1000]上单调递减,
因此f(x)≤f(10)≈-0.3167<0,即y=log7x+1≤0.25x.
所以,当x∈[10,1000]时,y≤0.25x,说明按模型y=log7x+1奖励 ,奖金不会超过利润的25%.
综上所述,模型y=log7x+1确实能符合公司要求 .
归纳总结
[规律方法] 自建模型时主要抓住四个关键:“求什么,设什么,列什么,限制什么”.
“求什么”就是弄清楚要解决什么问题,完成什么任务.
“设什么”就是弄清楚这个问题有哪些因素,谁是核心因素,通常设核心因素为自变量.
“列什么”就是把问题已知条件用所设变量表示出来,可以是方程、函数、不等式等.
“限制什么”主要是指自变量所应满足的限制条件,在实际问题中,除了要使函数式有意义外,还要考虑变量的实际含义,如人不能是半个等.
当堂达标
1、一辆汽车在某段路程中的行驶路程s关于时间t变化的图象如图所示,那么图象所对应的函数模型是( )
A.分段函数 B.二次函数 C.指数函数 D.对数函数
A
由图可知,该图象所对应的函数模型是分段函数模型.
2、若镭经过100年后剩留原来质量的95.76%,设质量为1的镭经过x年后剩留量为y,则x,y的函数关系是( )
A
3、若一根蜡烛长20cm,点燃后每小时燃烧5cm,则燃烧剩下的高度h(cm)与燃烧时间t(h)的函数关系用图象表示为( )
B [由题意h=20-5t(0≤t≤4),其图象为B.]
4、某工厂生产某种产品固定成本为2000万元,并且每生产一单位产品,成本增加10万元.又知总收入K是单位产品数Q的函数, ,则总利润L(Q)的最大值是________万元.
∵每生产一单位产品,成本增加10万元,∴单位产品数Q时的总成本为2000+10Q万元.
2500
∴Q=300时,利润L(Q)的最大值是2 500万元.
5、已知A,B两地相距150 km,某人开汽车以60 km/h的速度从A地到达B地,在B地停留1小时后再以50 km/h的速度返回A地.(1)把汽车离开A地的距离s表示为时间t的函数(从A地出发时开始),并画出函数的图象;(2)把车速v(km/h)表示为时间t(h)的函数,并画出函数的图象.
解析:(1)
①汽车由A地到B地行驶th所走的距离s=60t(0≤t≤2.5).②汽车在B地停留1小时,则汽车到A地的距离s=150(2.5<t≤3.5).③由B地返回A地,则汽车到A地的距离s=150-50(t-3.5)=325-50t(3.5<t≤6.5).
实际应用问题
审 题
(设)
分析、联想、抽象、转化
构建数学模型
数学化
(列)
寻找解题思路
(解)
解答数学问题
还原
(答)
课堂小结
4.5.3 函数模型的应用
我们知道,函数是描述客观世界变化规律的数学模型,不同的变化规律需要用不同的函数模型来刻画.面临一个实际问题,该如何选择恰当的函数模型来刻画它呢?
温故知新
1、常见函数模型
常用函数模型 (1)一次函数模型 y=kx+b(k,b为常数,k≠0)
(2)二次函数模型 y=ax2+bx+c(a,b,c为常数,a≠0)
(3)指数函数模型 y=bax+c(a,b,c为常数,b≠0,a>0且a≠1)
(4)对数函数模型 y=mlogax+n(m,a,n为常数,m≠0,a>0且a≠1)
(5)幂函数模型 y=axn+b(a,b为常数,a≠0)
(6)分段函数
2、建立函数模型解决问题的基本过程
思考:解决函数应用问题的基本步骤是什么?
利用函数知识和函数观点解决实际问题时,一般按以下几个步骤进行:
(一)审题;
(二)建模;
(三)求模;
(四)还原.
这些步骤用框图表示如图:
思考:解决函数应用问题的基本步骤是什么?
例3、人口问题是当今世界各国普遍关注的问题.认识人口数量的变化规律,可以为制定一系列相关政策提供依据.早在 1978 年,英国经济学家马尔萨斯(T.R.Malthas,1766—1834)就提出了自然状态下的人口增长模型y=y0ert,其中t表示经过的时间,y0表示t=0时的人口数,r表示人口的年平均增长率.下表是1950~1959年我国的人口数据资料
(1)如果以各年人口增长率的平均值作为我国这一时期的人口增长率 (精确到0.0001),用马尔萨斯人口增长模型建立我国在这一时期的具体人口增长模型,并检验所得模型与实际人口数据是否相符;
(2)如果按上表的增长趋势,那么大约在哪一年我国的人口数达到13亿?
典例解析
分析:用马尔萨斯人口增长模型建立具体人口增长模型,就是要确定其中的初始量y0和年平均增长率r.
解:(1)设1951~1959年我国各年的人口增长率分别为r1,r2,…,r9.
由55196(1+r1)=56300可得1951年的人口增长率r1≈0.0200.
同理可得,r2≈0.0210,r3≈0.0229,r4≈0.0250,r5≈0.0197,
r6≈0.0223,r7≈0.0276,r8≈0.0222,r9≈0.0154.
于是,1951~1959年期间,
我国人口的年平均增长率为:
r=(r1+r2+…+r9)÷9≈0.0221
令y0=55196,
则我国在1950~1959年期间的人口增长模型为y=55196e0.0221t,t∈N.
根据表中的数据画出散点图,并画出函数y=55196e0.0221t(t∈N)的图象,由图可以看出,所得模型与1950~1959年的实际人口数据基本吻合 .
事实上,我国1989年的人口数为11.27亿,直到2005年才突破13亿.对由函数模型所得的结果与实际情况不符 , 你有何看法 ?
因为人口基数较大,人口增长过快,与我国经济发展水平产生了较大矛盾,所以我国从20世纪70年代逐步实施了计划生育政策.因此这一阶段的人口增长条件并不符合马尔萨斯人口增长模型的条件,自然就出现了依模型得到的结果与实际不符的情况.
(2)如果按上表的增长趋势,那么大约在t=39,即1989年我国的人口数达到13亿.
例4、2010年,考古学家对良渚古城水利系统中一条水坝的建筑材料上提取的草茎遗存进行碳14年代学检测,检测出碳 14的残留量约为初始量的55.2%,能否以此推断此水坝大概是什么年代建成的
分析:因为死亡生物机体内碳14的初始量按确定的衰减率衰减,属于指数衰减,所以应选择函数y=kax(k∈R,且k≠0;a>0,且a≠1)建立数学模型.
解:设样本中碳14的初始量为k,衰减率为p(0
典例解析
于是 ,所以
由样本中碳14 的残余量约为初始量的55.2%可知 ,即
解得 .由计算工具得x≈4912.
因为2010年之前的4912年是公元前2902年,所以推断此水坝大概是公元前2902年建成的.
归纳总结
[规律方法]已知函数模型解决实际问题,往往给出的函数解析式含有参数,需要将题中的数据代入函数模型,求得函数模型中的参数,再将问题转化为已知函数解析式求函数值或自变量的值.
例5、假设你有一笔资金用于投资,现有三种投资方案供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
请问,你会选择哪种投资方案?
①问题中涉及哪些数量关系?
②如何用函数描述这些数量关系?
投资天数、回报金额
日回报
累计回报
典例解析
40
40
40
40
40
10
10+10
=10×2
10+10+10
=10×3
10+10+10+10
=10×4
10+10+10+10+10
=10×5
0.4
0.4×2
0.4×2×2
=0.4×22
0.4×2×2×2
=0.4×23
0.4×2×2×2×2
=0.4×24
方案一
方案二
方案三
1
2
3
4
5
则方案一可以用函数________________进行描述;
方案二可以用函数__________________进行描述;
方案三可以用函数___________________进行描述。
设第x天的回报是y元,
y=40 (x∈N*)
y=10x (x∈N*)
y=0.4×2x-1 (x∈N*)
三种方案每天回报表
x/天 方案1 方案2 方案3 y/元 增加量/元 y/元 增加量/元 y/元 增加量/元
1 40 10 0.4
2 40 0 20 10 0.8 0.4
3 40 0 30 10 1.6 0.8
4 40 0 40 10 3.2 1.6
5 40 0 50 10 6.4 3.2
6 40 0 60 10 12.8 6.4
7 40 0 70 10 25.6 12.8
8 40 0 80 10 51.2 25.6
9 40 0 90 10 102.4 51.2
10 40 0 100 10 204.8 102.4
… … … … … … …
30 40 0 300 10 214748365 107374182.4
0
x
y
20
40
60
80
100
120
140
4
2
6
8
10
12
1 2 3 4 5 6 7 8 9 10 11 … 30
方案一 40 80 120 160 200 240 280 320 360 400 440 … 1200
方案二 10 30 60 100 150 210 280 360 450 550 660 … 4650
方案三 0 1 2.8 6 12 25 50.8 102 204 409 819 … 429496729.2
例5 累计回报表
投资1~6天,应选择方案一;
投资7天,应选择方案一或方案二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三。
假如某公司每天给你投资1万元,共投资30天。公司要求你给他的回报是:第一天给公司1分钱,第二天给公司2分钱,以后每天给的钱都是前一天的2倍,共30天,你认为这样的交易对你有利吗?
你30天内给公司的回报为:
0.01+0.01×2+0.01×22+…+0.01×229
=10737418.23
≈1074(万元)
30万元
解答如下:公司30天内为你的总投资为:
上述例子只是一种假想情况,但从中可以看到,不同的函数增长模型,增长变化存在很大差异
一次函数,
对数型函数,
指数函数。
①例6涉及了哪几类函数模型?
②你能用数学语言描述符合公司奖励方案的条件吗
例6、某公司为了实现1000万元利润的目标,准备制定一个激励销售人员的奖励方案:在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金总数不超过5万元,同时奖金不超过利润的25%。
现有三个奖励模型:y=0.25x, y=log7x+1, y=1.002x,其中哪个模型能符合公司的要求?
典例解析
分析:本例提供了三个不同增长方式的奖励模型,按要求选择其中一个函数作为刻画奖金总数与销售利润的关系.由于公司总的利润目标为1000万元,所以销售人员的销售利润一般不会超过公司总的利润.于是,只需在区间[10,1000]上,寻找并验证所选函数是否满足两条要求 :
第一,奖金总数不超过5万元,即最大值不大于5;
第二,奖金不超过利润的25%,即y≤0.25x.不妨先画出函数图象,通过观察函数图象,得到初步的结论,再通过具体计算,确认结果.
解:借助信息技术画出函数y=5,y=0.25x,y=log7x+1,y=1.002x的图象. 观察图象发现,在区间[10,1000]上 , 模型y=0.25x,y=1.002x的图象都有一部分在直线y=5的上方 , 只有模型y=log7x+1的图象始终在y=5的下方 , 这说明只有按模型y=log7x+1进行奖励时才符合公司的要求 .
下面通过计算确认上述判断 .
先计算哪个模型的奖金总数不超过5万元 .
对于模型y=0.25x, 它在区间[10,1000]上单调递增 , 而且当x=20时,y=5,
因此,当x>20时,y>5,所以该模型不符合要求 ;
对于模型y=1.002x,由函数图象,并利用信息技术,可知在区间(805,806)内有一个点x0满足1.002x0=5,由于它在区间[10,1000]上单调递增,因此当x>x0时,y>5,所以该模型也不符合要求 ;
对于模型y=log7x+1,它在区间[10,1000]上单调递增,而且当x=1000 时 ,y=log71000+1≈4.55<5 , 所以它符合奖金总数不超过5万元的要求 .
再计算按模型y=log7x+1奖励时, 奖金是否不超过利润的25% ,即当x∈[10,1000]时,是否有y≤0.25x,
即y=log7x+1≤0.25x成立 .
令f(x)=log7x+1-0.25x,x∈[10,1000],
利用信息技术画出它的图象
由图象可知函数f(x)在区间[10,1000]上单调递减,
因此f(x)≤f(10)≈-0.3167<0,即y=log7x+1≤0.25x.
所以,当x∈[10,1000]时,y≤0.25x,说明按模型y=log7x+1奖励 ,奖金不会超过利润的25%.
综上所述,模型y=log7x+1确实能符合公司要求 .
归纳总结
[规律方法] 自建模型时主要抓住四个关键:“求什么,设什么,列什么,限制什么”.
“求什么”就是弄清楚要解决什么问题,完成什么任务.
“设什么”就是弄清楚这个问题有哪些因素,谁是核心因素,通常设核心因素为自变量.
“列什么”就是把问题已知条件用所设变量表示出来,可以是方程、函数、不等式等.
“限制什么”主要是指自变量所应满足的限制条件,在实际问题中,除了要使函数式有意义外,还要考虑变量的实际含义,如人不能是半个等.
当堂达标
1、一辆汽车在某段路程中的行驶路程s关于时间t变化的图象如图所示,那么图象所对应的函数模型是( )
A.分段函数 B.二次函数 C.指数函数 D.对数函数
A
由图可知,该图象所对应的函数模型是分段函数模型.
2、若镭经过100年后剩留原来质量的95.76%,设质量为1的镭经过x年后剩留量为y,则x,y的函数关系是( )
A
3、若一根蜡烛长20cm,点燃后每小时燃烧5cm,则燃烧剩下的高度h(cm)与燃烧时间t(h)的函数关系用图象表示为( )
B [由题意h=20-5t(0≤t≤4),其图象为B.]
4、某工厂生产某种产品固定成本为2000万元,并且每生产一单位产品,成本增加10万元.又知总收入K是单位产品数Q的函数, ,则总利润L(Q)的最大值是________万元.
∵每生产一单位产品,成本增加10万元,∴单位产品数Q时的总成本为2000+10Q万元.
2500
∴Q=300时,利润L(Q)的最大值是2 500万元.
5、已知A,B两地相距150 km,某人开汽车以60 km/h的速度从A地到达B地,在B地停留1小时后再以50 km/h的速度返回A地.(1)把汽车离开A地的距离s表示为时间t的函数(从A地出发时开始),并画出函数的图象;(2)把车速v(km/h)表示为时间t(h)的函数,并画出函数的图象.
解析:(1)
①汽车由A地到B地行驶th所走的距离s=60t(0≤t≤2.5).②汽车在B地停留1小时,则汽车到A地的距离s=150(2.5<t≤3.5).③由B地返回A地,则汽车到A地的距离s=150-50(t-3.5)=325-50t(3.5<t≤6.5).
实际应用问题
审 题
(设)
分析、联想、抽象、转化
构建数学模型
数学化
(列)
寻找解题思路
(解)
解答数学问题
还原
(答)
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
