2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.4.2.2 用空间向量研究夹角问题课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.4.2.2 用空间向量研究夹角问题课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:37:23 | ||
图片预览




文档简介
(共17张PPT)
1.4.2.2 用空间向量研究夹角问题
复习回顾
1.空间两点之间的距离
2. 点到直线的距离
两条平行直线的距离
思考:两条异面直线的距离怎么求?
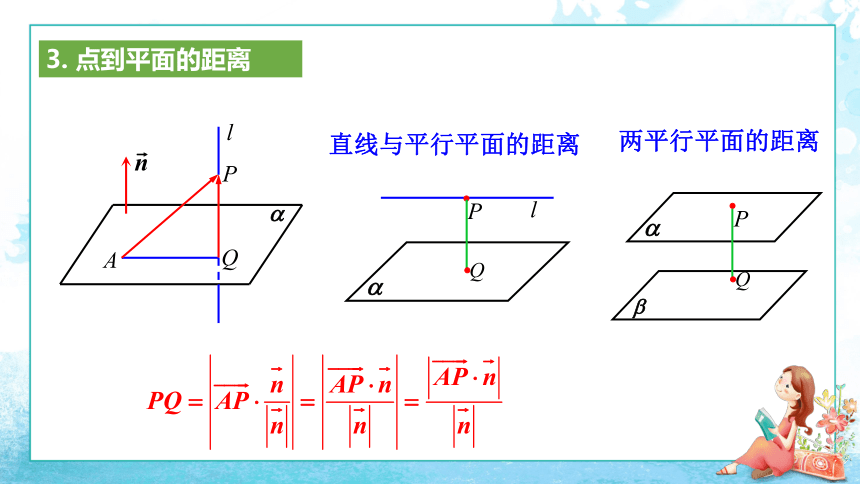
3. 点到平面的距离
A
P
Q
l
l
直线与平行平面的距离
两平行平面的距离
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何结论.
(化为向量问题)
(进行向量运算)
(回到图形)
用空间向量解决立体几何问题的“三步曲”:
与距离类似,角度是立体几何中另一个重要的度量.
下面我们用向量方法研究直线与直线所成的角、直线与平面所成的角以及平面与平面的夹角.
直接引入
先回顾一下向量与向量所成的角如何求?
C
A
B
D
M
N
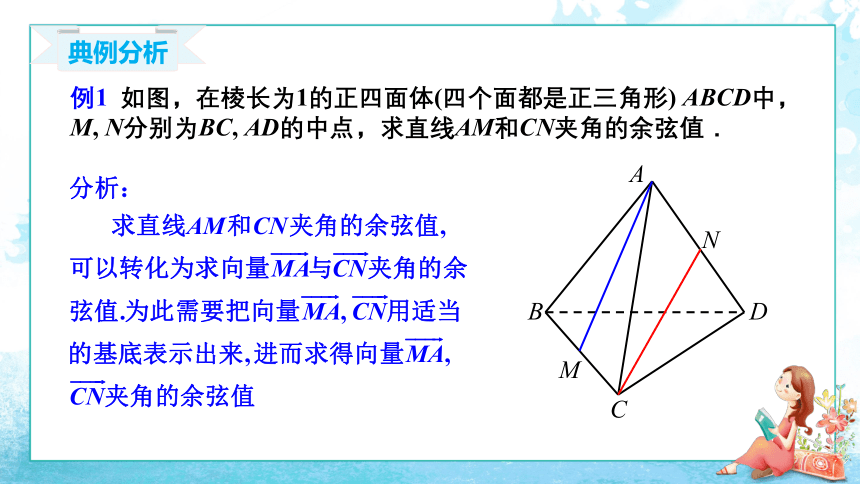
例1 如图,在棱长为1的正四面体(四个面都是正三角形) ABCD中, M, N分别为BC, AD的中点,求直线AM和CN夹角的余弦值.
典例分析
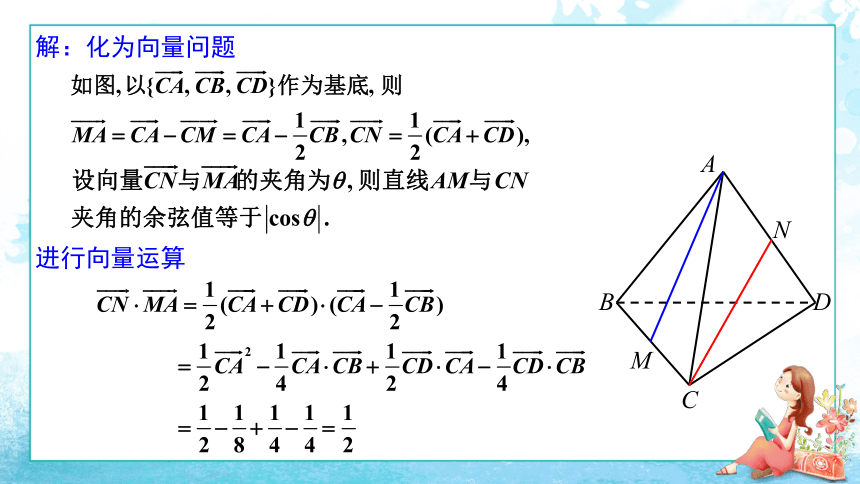
解:化为向量问题
C
A
B
D
M
N
进行向量运算
C
A
B
D
M
N
回到图形问题
探究新知
思考:我们在例1用向量方法解决了异面直线AM和CN所成角的问题,你能用向量方法求直线AB与平面BCD所成的角吗?
探究新知
C
A
B
D
M
N
A
B
C
探究新知
探究新知
思考:图中有几个二面角?两个平面的夹角与这两个平面形成的二面角有什么关系?
探究新知
A
B
C
C1
A1
B1
x
y
z
P
Q
R
典例分析
解:化为向量问题
A
B
C
C1
A1
B1
x
y
z
P
Q
R
进行向量运算
y
回到图形问题
课堂小结
1.4.2.2 用空间向量研究夹角问题
复习回顾
1.空间两点之间的距离
2. 点到直线的距离
两条平行直线的距离
思考:两条异面直线的距离怎么求?
3. 点到平面的距离
A
P
Q
l
l
直线与平行平面的距离
两平行平面的距离
(1)建立立体图形与空间向量的联系,用空间向量表示问题中涉及的点、直线、平面,把立体几何问题转化为向量问题;
(2)通过向量运算,研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题;
(3)把向量的运算结果“翻译”成相应的几何结论.
(化为向量问题)
(进行向量运算)
(回到图形)
用空间向量解决立体几何问题的“三步曲”:
与距离类似,角度是立体几何中另一个重要的度量.
下面我们用向量方法研究直线与直线所成的角、直线与平面所成的角以及平面与平面的夹角.
直接引入
先回顾一下向量与向量所成的角如何求?
C
A
B
D
M
N
例1 如图,在棱长为1的正四面体(四个面都是正三角形) ABCD中, M, N分别为BC, AD的中点,求直线AM和CN夹角的余弦值.
典例分析
解:化为向量问题
C
A
B
D
M
N
进行向量运算
C
A
B
D
M
N
回到图形问题
探究新知
思考:我们在例1用向量方法解决了异面直线AM和CN所成角的问题,你能用向量方法求直线AB与平面BCD所成的角吗?
探究新知
C
A
B
D
M
N
A
B
C
探究新知
探究新知
思考:图中有几个二面角?两个平面的夹角与这两个平面形成的二面角有什么关系?
探究新知
A
B
C
C1
A1
B1
x
y
z
P
Q
R
典例分析
解:化为向量问题
A
B
C
C1
A1
B1
x
y
z
P
Q
R
进行向量运算
y
回到图形问题
课堂小结
