2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.4.2.3 用向量方法解决立体几何问题的综合应用课件(共11张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.4.2.3 用向量方法解决立体几何问题的综合应用课件(共11张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:38:34 | ||
图片预览




文档简介
(共11张PPT)
1.4.2.3 用向量方法解决立体几何问题的综合应用
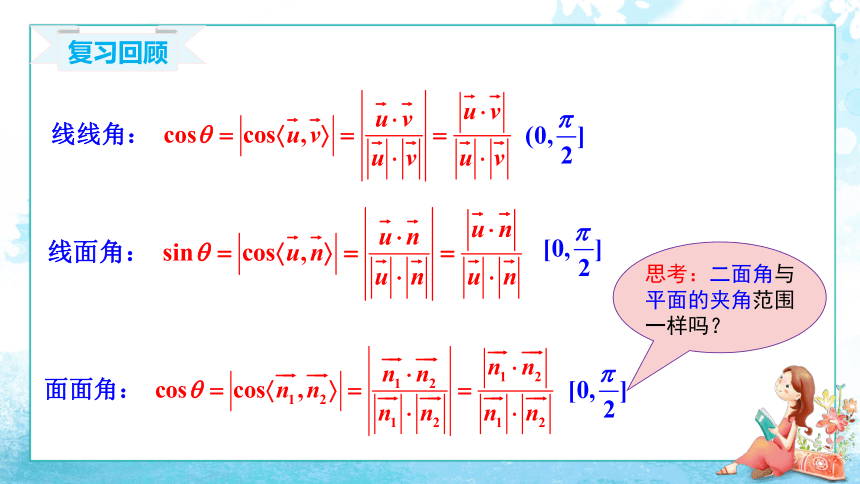
复习回顾
思考:二面角与平面的夹角范围一样吗?
直接引入
前面我们学习了如何用向量方法求解立体几何中的距离和角度问题.这节课我们应用这些知识解决综合性较强的问题.
下面先看一道生活中的实际问题,思考如何转化为数学问题来进行解决.
例9 下图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为30°,已知礼物的质量为1 kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度g取9.8 m/s2,精确到0.01 N).
思考下列问题:
1.降落伞匀速下落,下落过程中,8根绳子拉力的合力大小与礼物重力大小有什么关系?
2.每根绳子的拉力和合力有什么关系?
3.如何用向量方法解决这个问题?
典例分析
8根绳子的拉力在水平面的法向量方向上的投影向量的和向量与礼物的重力是一对相反向量.
A
B
C
D
E
F
G
P
z
x
y
分析: 本题涉及的问题包括:直线与平面平行和垂直的判定,计算两个平面的夹角,这些问题都可以利用向量方法解决.由于四棱锥的底面是正方形,而且一条侧棱垂直于底面,可以利用这些条件建立适当的空间直角坐标系,用向量及坐标表示问题中的几何元素,进而解决问题.
典例分析
A
B
C
D
E
F
G
P
z
x
y
A
B
C
D
E
F
G
P
z
x
y
A
B
C
D
E
F
G
P
z
x
y
用空间向量表示立体图形中点、直线、平面等元素
进行空间向量的运算,研究点、直线、平面之间的关系
把运算结果“翻译”成相应的几何意义
1.通过本节的学习,向量方法解决立体几何问题的基本步骤是什么?你能用框图表示吗?
课堂小结
2.解决立体几何中的问题,可用三种方法:综合法、向量法、坐标法.你能说出它们各自的特点吗?
综合法以逻辑推理作为工具解决问题;向量法利用向量的概念及其运算解决问题,如本节的例7、例9;坐标法利用数及其运算来解决问题,坐标法经常与向量法结合起来使用,如本节的例6,例8,例10.对于具体的问题,应根据它的条件和所求选择合适的方法.
1.4.2.3 用向量方法解决立体几何问题的综合应用
复习回顾
思考:二面角与平面的夹角范围一样吗?
直接引入
前面我们学习了如何用向量方法求解立体几何中的距离和角度问题.这节课我们应用这些知识解决综合性较强的问题.
下面先看一道生活中的实际问题,思考如何转化为数学问题来进行解决.
例9 下图为某种礼物降落伞的示意图,其中有8根绳子和伞面连接,每根绳子和水平面的法向量的夹角均为30°,已知礼物的质量为1 kg,每根绳子的拉力大小相同.求降落伞在匀速下落的过程中每根绳子拉力的大小(重力加速度g取9.8 m/s2,精确到0.01 N).
思考下列问题:
1.降落伞匀速下落,下落过程中,8根绳子拉力的合力大小与礼物重力大小有什么关系?
2.每根绳子的拉力和合力有什么关系?
3.如何用向量方法解决这个问题?
典例分析
8根绳子的拉力在水平面的法向量方向上的投影向量的和向量与礼物的重力是一对相反向量.
A
B
C
D
E
F
G
P
z
x
y
分析: 本题涉及的问题包括:直线与平面平行和垂直的判定,计算两个平面的夹角,这些问题都可以利用向量方法解决.由于四棱锥的底面是正方形,而且一条侧棱垂直于底面,可以利用这些条件建立适当的空间直角坐标系,用向量及坐标表示问题中的几何元素,进而解决问题.
典例分析
A
B
C
D
E
F
G
P
z
x
y
A
B
C
D
E
F
G
P
z
x
y
A
B
C
D
E
F
G
P
z
x
y
用空间向量表示立体图形中点、直线、平面等元素
进行空间向量的运算,研究点、直线、平面之间的关系
把运算结果“翻译”成相应的几何意义
1.通过本节的学习,向量方法解决立体几何问题的基本步骤是什么?你能用框图表示吗?
课堂小结
2.解决立体几何中的问题,可用三种方法:综合法、向量法、坐标法.你能说出它们各自的特点吗?
综合法以逻辑推理作为工具解决问题;向量法利用向量的概念及其运算解决问题,如本节的例7、例9;坐标法利用数及其运算来解决问题,坐标法经常与向量法结合起来使用,如本节的例6,例8,例10.对于具体的问题,应根据它的条件和所求选择合适的方法.
