2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.1.2 空间向量的数量积运算课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.1.2 空间向量的数量积运算课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 10:41:40 | ||
图片预览




文档简介
(共20张PPT)
1.1.2 空间向量的数量积运算
复习引入
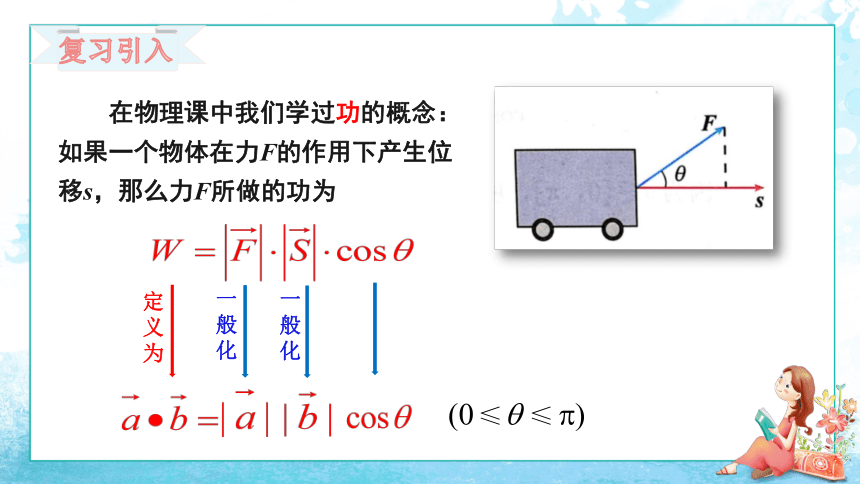
在物理课中我们学过功的概念:如果一个物体在力F的作用下产生位移s,那么力F所做的功为
一般化
一般化
定义为
平面向量的数量积 性质
几何 意义
运算律
A
C
D
A1
B1
B
a
b
O
B
A
O
B
A
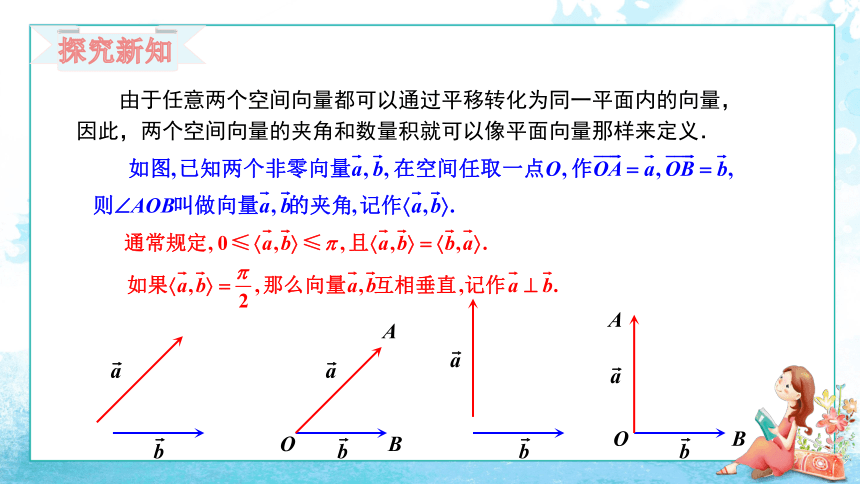
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
探究新知
特别地,零向量与任意向量的数量积为0.
探究新知
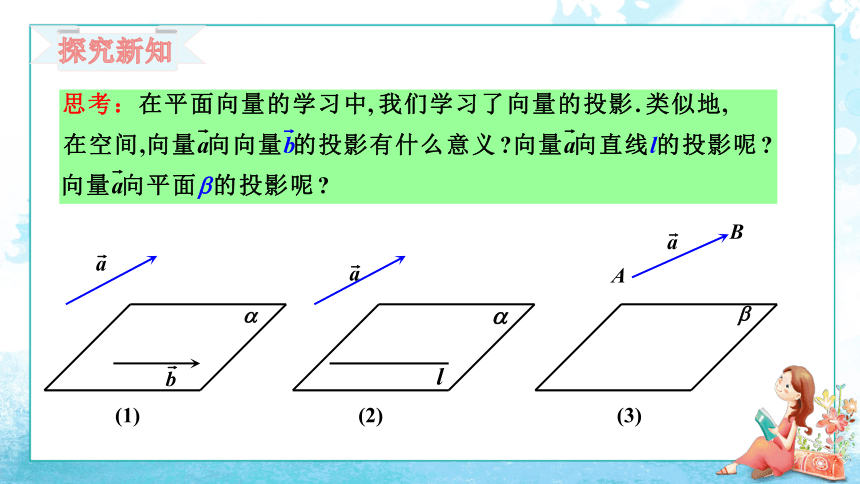
探究新知
(1)
(2)
A
B
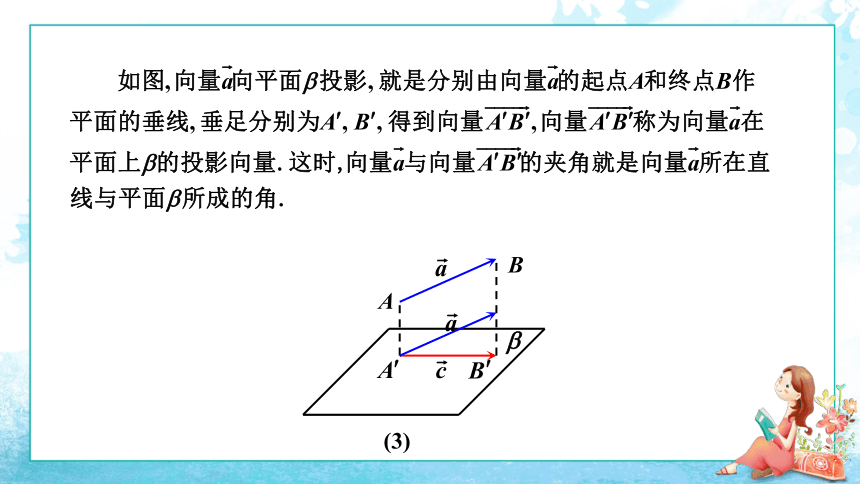
(3)
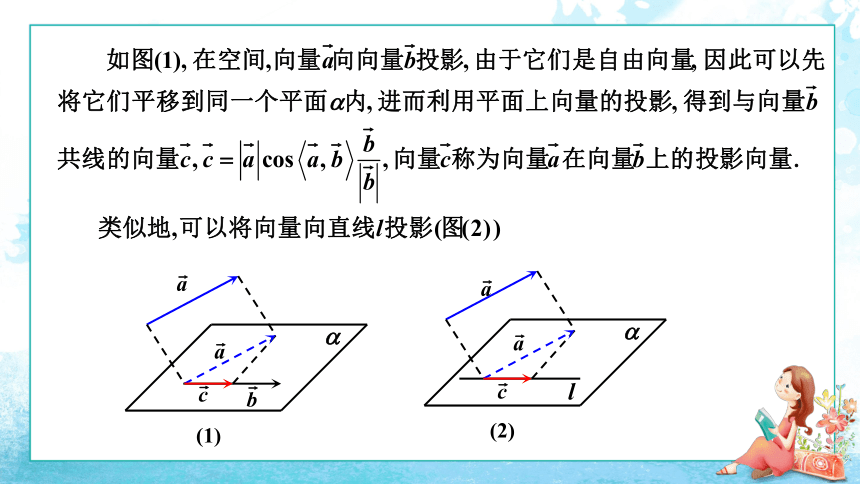
(1)
(2)
A
B
(3)
探究新知
a
c
b
不能
探究新知
不能
向量没有除法运算,因为有两种乘法:一是数量积a·b,二是向量积a×b,所以向量的除法没有意义.
不成立
当a与c共线时,(a·b)·c=a·(b·c)成立;
当a与c不共线时,(a·b)·c≠a·(b·c).
因此,(a·b)·c=a·(b·c)不一定成立.
向量的数量积不满足结合律.
证明:
A
B
C
D
典例分析
l
m
n
g
典例分析
l
m
n
g
A
B
C
C1
A1
B1
B
课堂练习
B
D
A
C
A
B
C
D
A
B
D
C
a
c
b
空间向量的数量积
空间两个向量的夹角
定义
几何意义
运算律
性质
利用向量解决立体几何问题的应用
课堂小结
1.1.2 空间向量的数量积运算
复习引入
在物理课中我们学过功的概念:如果一个物体在力F的作用下产生位移s,那么力F所做的功为
一般化
一般化
定义为
平面向量的数量积 性质
几何 意义
运算律
A
C
D
A1
B1
B
a
b
O
B
A
O
B
A
由于任意两个空间向量都可以通过平移转化为同一平面内的向量,因此,两个空间向量的夹角和数量积就可以像平面向量那样来定义.
探究新知
特别地,零向量与任意向量的数量积为0.
探究新知
探究新知
(1)
(2)
A
B
(3)
(1)
(2)
A
B
(3)
探究新知
a
c
b
不能
探究新知
不能
向量没有除法运算,因为有两种乘法:一是数量积a·b,二是向量积a×b,所以向量的除法没有意义.
不成立
当a与c共线时,(a·b)·c=a·(b·c)成立;
当a与c不共线时,(a·b)·c≠a·(b·c).
因此,(a·b)·c=a·(b·c)不一定成立.
向量的数量积不满足结合律.
证明:
A
B
C
D
典例分析
l
m
n
g
典例分析
l
m
n
g
A
B
C
C1
A1
B1
B
课堂练习
B
D
A
C
A
B
C
D
A
B
D
C
a
c
b
空间向量的数量积
空间两个向量的夹角
定义
几何意义
运算律
性质
利用向量解决立体几何问题的应用
课堂小结
