2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.2空间向量基本定理(第一课时)课件(20张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册1.2空间向量基本定理(第一课时)课件(20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 09:58:27 | ||
图片预览





文档简介
(共20张PPT)
1.2 空间向量基本定理
2.平面向量的正交分解
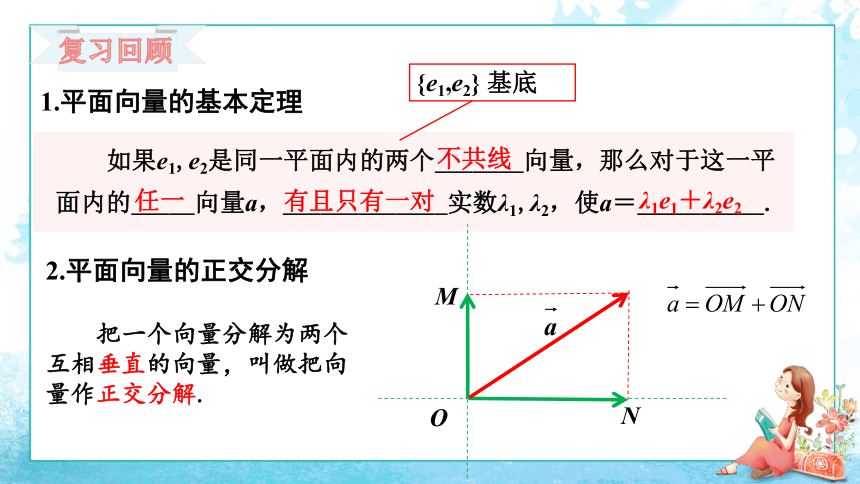
如果e1,e2是同一平面内的两个_______向量,那么对于这一平面内的_____向量a,_____________实数λ1,λ2,使a=__________.
1.平面向量的基本定理
不共线
任一
有且只有一对
λ1e1+λ2e2
{e1,e2} 基底
M
N
O
把一个向量分解为两个互相垂直的向量,叫做把向量作正交分解.
复习回顾
我们先从空间中三个不共面的向量两两垂直这一特殊情况开始讨论.
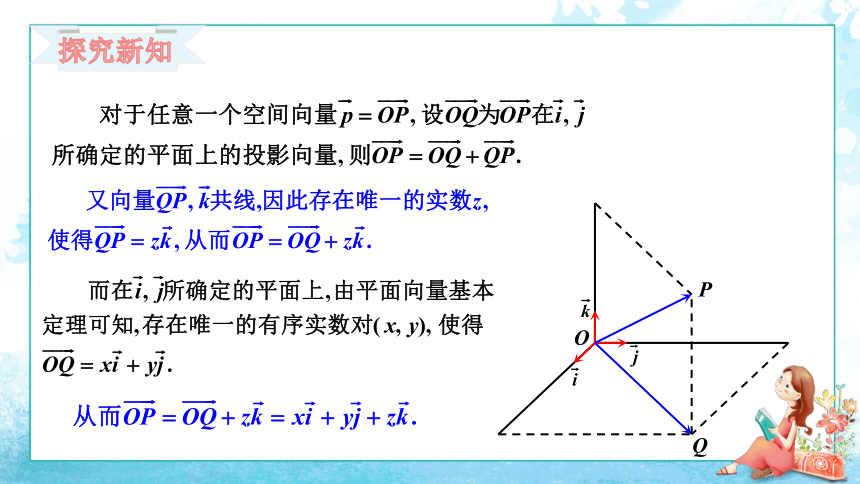
探究新知
O
O
P
Q
探究新知
O
P
Q
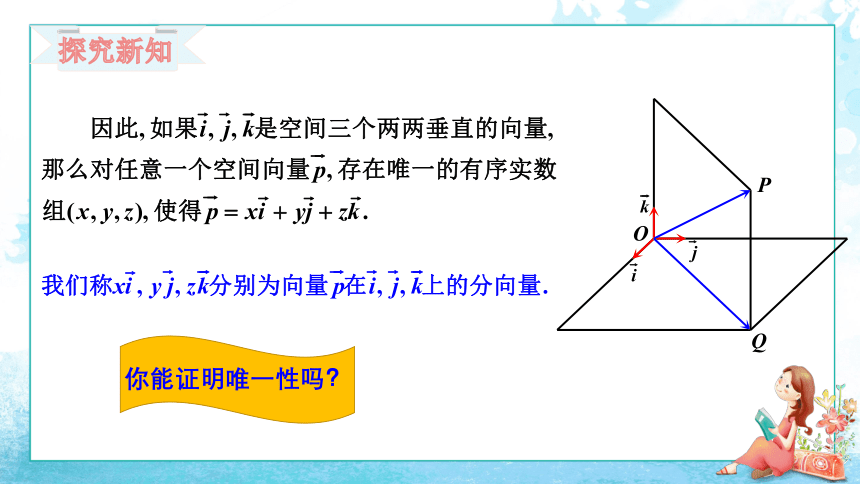
你能证明唯一性吗?
探究新知
+zk +z1k
反证法
假设存在x1,y1,z1使得+z1k也成立
+z1k-zk
整理+z1-zk
不妨不相等
所以+k
,k 共面,与已知矛盾.
证明:
矛盾在哪里?
共面
探究新知
【空间向量基本定理】
如果三个向量 不共面,那么对任意一个空间向量 ,存在唯一的有序实数组( x,y,z),使得
请你自己给出空间向量基本定理的证明.
过P'作直线P'A'平行于直线OB,
作直线P'B'平行于直线OA,
作直线P'C'平行于直线OP',
p
P
P ′
A′
B′
C′
a
O
A
c
C
b
B
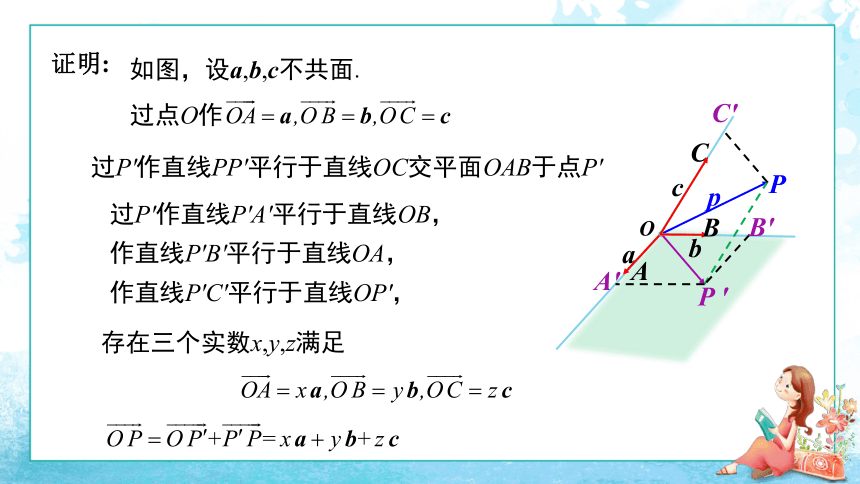
证明:
如图,设a,b,c不共面.
过点O作
过P'作直线PP'平行于直线OC交平面OAB于点P'
存在三个实数x,y,z满足
阅读教材,回答下列问题:
(1)什么是基底?什么是基向量?
(2)一个基底包含几个基向量?三个向量要构成一个基底需要满足什么条件?
(3)什么是单位正交基底?
(4)正交分解的定义是什么?
探究新知
(1)什么是基底?什么是基向量?
(2)一个基底包含几个基向量?三个向量要构成一个基底需要满足什么条件?
(3)什么是单位正交基底?
(4)正交分解的定义是什么?
空间向量间的运算 基向量间的运算
转化
C
A
B
M
N
P
O
典例分析
A
B
C
D
M
N
B1
A1
C1
D1
典例分析
A
B
C
D
M
N
B1
A1
C1
D1
C
A
B
D
E
F
G
典例分析
C
A
B
D
E
F
G
C
A
B
D
E
F
G
1. 已知向量 是空间的一个基底.求证:向量 能构成空间的一个基底.
课堂练习
课堂练习
2.如图,已知平行六面体OABC-O'A'B'C',点G是侧面BB'C'C的中心,且
(1) 是否构成空间的一个基底?
(2)如果 构成空间的一个基底,那么用它表示下列向量:
B
C
O
A1
B1
C1
O1
A
G
课堂小结
1.2 空间向量基本定理
2.平面向量的正交分解
如果e1,e2是同一平面内的两个_______向量,那么对于这一平面内的_____向量a,_____________实数λ1,λ2,使a=__________.
1.平面向量的基本定理
不共线
任一
有且只有一对
λ1e1+λ2e2
{e1,e2} 基底
M
N
O
把一个向量分解为两个互相垂直的向量,叫做把向量作正交分解.
复习回顾
我们先从空间中三个不共面的向量两两垂直这一特殊情况开始讨论.
探究新知
O
O
P
Q
探究新知
O
P
Q
你能证明唯一性吗?
探究新知
+zk +z1k
反证法
假设存在x1,y1,z1使得+z1k也成立
+z1k-zk
整理+z1-zk
不妨不相等
所以+k
,k 共面,与已知矛盾.
证明:
矛盾在哪里?
共面
探究新知
【空间向量基本定理】
如果三个向量 不共面,那么对任意一个空间向量 ,存在唯一的有序实数组( x,y,z),使得
请你自己给出空间向量基本定理的证明.
过P'作直线P'A'平行于直线OB,
作直线P'B'平行于直线OA,
作直线P'C'平行于直线OP',
p
P
P ′
A′
B′
C′
a
O
A
c
C
b
B
证明:
如图,设a,b,c不共面.
过点O作
过P'作直线PP'平行于直线OC交平面OAB于点P'
存在三个实数x,y,z满足
阅读教材,回答下列问题:
(1)什么是基底?什么是基向量?
(2)一个基底包含几个基向量?三个向量要构成一个基底需要满足什么条件?
(3)什么是单位正交基底?
(4)正交分解的定义是什么?
探究新知
(1)什么是基底?什么是基向量?
(2)一个基底包含几个基向量?三个向量要构成一个基底需要满足什么条件?
(3)什么是单位正交基底?
(4)正交分解的定义是什么?
空间向量间的运算 基向量间的运算
转化
C
A
B
M
N
P
O
典例分析
A
B
C
D
M
N
B1
A1
C1
D1
典例分析
A
B
C
D
M
N
B1
A1
C1
D1
C
A
B
D
E
F
G
典例分析
C
A
B
D
E
F
G
C
A
B
D
E
F
G
1. 已知向量 是空间的一个基底.求证:向量 能构成空间的一个基底.
课堂练习
课堂练习
2.如图,已知平行六面体OABC-O'A'B'C',点G是侧面BB'C'C的中心,且
(1) 是否构成空间的一个基底?
(2)如果 构成空间的一个基底,那么用它表示下列向量:
B
C
O
A1
B1
C1
O1
A
G
课堂小结
