新疆维吾尔自治区喀什地区莎车县第一学校2022届高三上学期第三次质量检测数学试题(Word版含答案)
文档属性
| 名称 | 新疆维吾尔自治区喀什地区莎车县第一学校2022届高三上学期第三次质量检测数学试题(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 353.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 00:00:00 | ||
图片预览


文档简介
莎车县第一学校2022届高三上学期第三次质量检测
数学试题
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.若复数,其中为虚数单位,则( )
A. B. C. D.
3.命题“ x0∈(0,+∞),”的否定是( )
A. x∈(﹣∞,0),2x+sinx≥0
B. x∈(0,+∞),2x+sinx≥0
C. x0∈(0,+∞),
D. x0∈(﹣∞,0),
4.已知非零向量与满足且,则为( )
A.三边均不相等的三角形 B.直角三角形
C.等腰非等边三角形 D.等边三角形
5.f(x)是定义在R上的奇函数,且,为的导函数,且当时,则不等式f(x﹣1)>0的解集为( )
A.(0,1)∪(2,+∞) B.(﹣∞,1)∪(1,+∞)
C.(﹣∞,1)∪(2,+∞) D.(﹣∞,0)∪(1,+∞)
6.某程序框图如图所示,该程序运行后输出的值是( )
A. B. C. D.
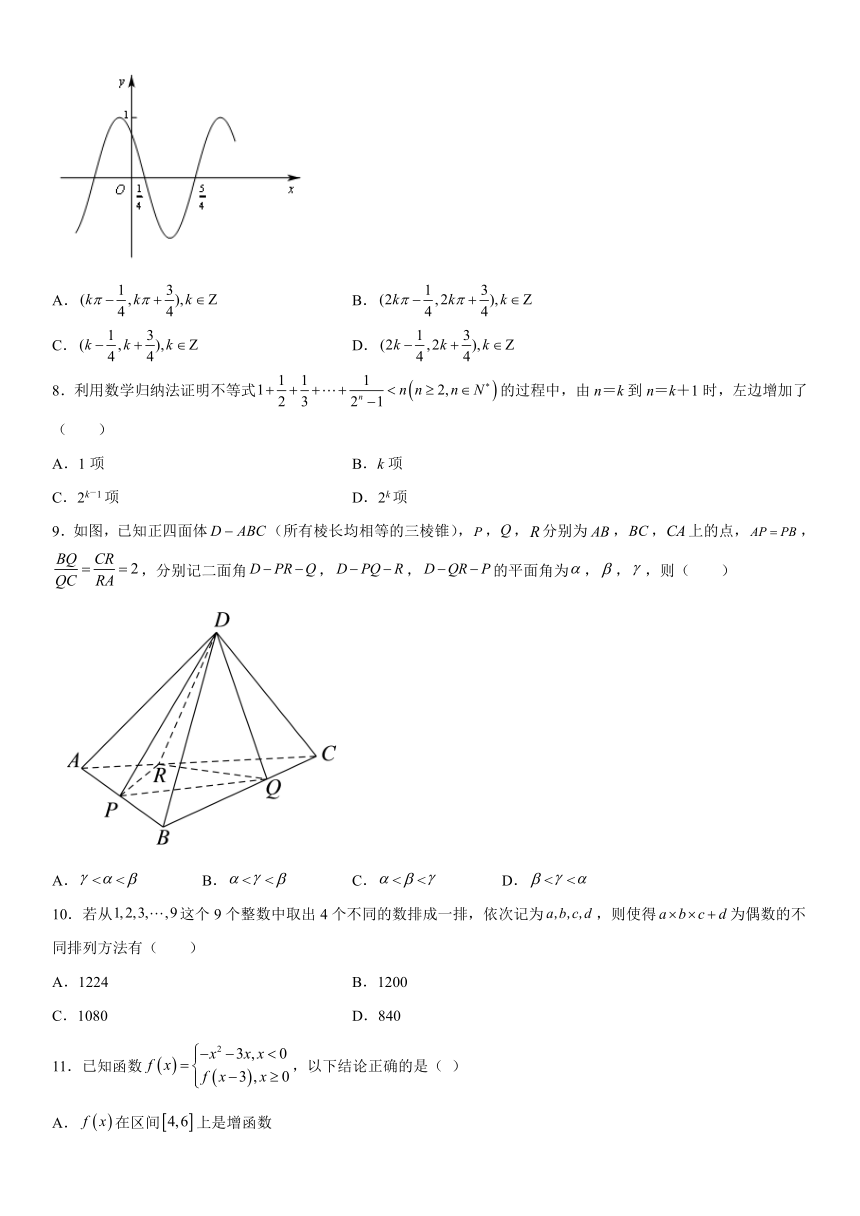
7.函数的部分图像如图所示,则的单调递减区间为( )
A. B.
C. D.
8.利用数学归纳法证明不等式的过程中,由n=k到n=k+1时,左边增加了( )
A.1项 B.k项
C.2k-1项 D.2k项
9.如图,已知正四面体(所有棱长均相等的三棱锥),,,分别为,,上的点,,,分别记二面角,,的平面角为,,,则( )
A.<< B.<< C.<< D.<<
10.若从这个9个整数中取出4个不同的数排成一排,依次记为,则使得为偶数的不同排列方法有( )
A.1224 B.1200
C.1080 D.840
11.已知函数,以下结论正确的是( )
A.在区间上是增函数
B.
C.若方程恰有个实根,则
D.若函数在上有 6个零点,则
12.已知函数在处取得极值,且,,若的单调递减区间为;则的取值范围为( )
A. B. C. D.
填空题:本题共4小题,每小题5分,共20分.
13.某工厂生产,,三种不同型号的产品,产品的数量之比依次为,现用分层抽样的方法抽出容量为的样本,样本中型产品有12件,那么样本容量为___________.
14.已知向量.若向量与垂直,则m=________.
15.已知定义在上的奇函数的导函数为,若,则实数的取值范围为___________.
16.函数的值域为________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知向量,函数()的最小正周期是.
(1)求的值及函数的单调递减区间;
(2)当时,求函数的值域.
18.如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向且与A相距10海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.
(1)求乙船每小时航行多少海里?
(2)在C处北偏西30°方向且与C相距海里处有一个暗礁E,暗礁E周围海里范围内为航行危险区域.问:甲、乙两船按原航向和速度航行有无危险?如有危险,从有危险开始多少小时后能脱离危险;如无危险,请说明理由.
19.为弘扬劳动精神,树立学生“劳动最美,劳动最光荣”的观念,某校持续开展“家庭劳动大比拼”活动.某班统计了本班同学1~7月份的人均月劳动时间(单位:小时),并建立了人均月劳动时间y关于月份x的线性回归方程,y与x的原始数据如表所示:
月份x 1 2 3 4 5 6 7
人均月劳动时间y 8 9 m 12 n 19 22
由于某些原因导致部分数据丢失,但已知.
(1)求m,n的值;
(2)求该班6月份人均月劳动时间数据的残差值(残差即样本数据与预测值之差).
参考公式:在线性回归方程中,.
20.学校举办运动会,某班有人报名参赛,其中人报名参加游泳比赛,人报名参加田径比赛,人报名参加球类比赛,同时报名参加游泳比赛和田径比赛的有人,同时报名参加田径比赛和球类比赛的有人,没有人同时报名参加这三项比赛.
(1)求同时报名参加游泳和球类比赛的学生人数;
(2)在只报名参加游泳一项比赛的人中,男生比女生多人,且男生甲和女生乙都在其中,现从这人中随机选出男女生各人,求男生甲被选中且女生乙未被选中的概率.
21.已知函数.
(1)当时,求曲线在点,处的切线方程;
(2)若存在,,使得不等式成立,求的取值范围.
22.在直角坐标系xOy中,以O为极点,x轴非负半轴为极轴,取相同单位长度,建立极坐标系.曲线C的极坐标方程为,M,N分别为C与x轴、y轴的交点.
(1)写出C的直角坐标方程,并求M,N的极坐标;
(2)设MN的中点为P,求直线OP的极坐标方程.
23.已知(,).
(1)当,时,解关于的不等式;
(2)若最小值为,求的最小值.
参考答案
1.A 2.A 3.B 4.D 5.A 6.B 7.D 8.D 9.B 10.A 11.C 12.D 13.60
14.7
15.
16.
17.(1),;(2).
18.(1)每小时30海里;(2)甲船没有危险,乙船有危险,且在遭遇危险开始持续小时后脱险,理由见解析.
19.(1)m=10,n=16;(2).
20.
(1)
(2)
21.(1);(2).
22.(1)见解析;(2)见解析
23.
(1)
(2)
数学试题
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.若复数,其中为虚数单位,则( )
A. B. C. D.
3.命题“ x0∈(0,+∞),”的否定是( )
A. x∈(﹣∞,0),2x+sinx≥0
B. x∈(0,+∞),2x+sinx≥0
C. x0∈(0,+∞),
D. x0∈(﹣∞,0),
4.已知非零向量与满足且,则为( )
A.三边均不相等的三角形 B.直角三角形
C.等腰非等边三角形 D.等边三角形
5.f(x)是定义在R上的奇函数,且,为的导函数,且当时,则不等式f(x﹣1)>0的解集为( )
A.(0,1)∪(2,+∞) B.(﹣∞,1)∪(1,+∞)
C.(﹣∞,1)∪(2,+∞) D.(﹣∞,0)∪(1,+∞)
6.某程序框图如图所示,该程序运行后输出的值是( )
A. B. C. D.
7.函数的部分图像如图所示,则的单调递减区间为( )
A. B.
C. D.
8.利用数学归纳法证明不等式的过程中,由n=k到n=k+1时,左边增加了( )
A.1项 B.k项
C.2k-1项 D.2k项
9.如图,已知正四面体(所有棱长均相等的三棱锥),,,分别为,,上的点,,,分别记二面角,,的平面角为,,,则( )
A.<< B.<< C.<< D.<<
10.若从这个9个整数中取出4个不同的数排成一排,依次记为,则使得为偶数的不同排列方法有( )
A.1224 B.1200
C.1080 D.840
11.已知函数,以下结论正确的是( )
A.在区间上是增函数
B.
C.若方程恰有个实根,则
D.若函数在上有 6个零点,则
12.已知函数在处取得极值,且,,若的单调递减区间为;则的取值范围为( )
A. B. C. D.
填空题:本题共4小题,每小题5分,共20分.
13.某工厂生产,,三种不同型号的产品,产品的数量之比依次为,现用分层抽样的方法抽出容量为的样本,样本中型产品有12件,那么样本容量为___________.
14.已知向量.若向量与垂直,则m=________.
15.已知定义在上的奇函数的导函数为,若,则实数的取值范围为___________.
16.函数的值域为________.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
17.已知向量,函数()的最小正周期是.
(1)求的值及函数的单调递减区间;
(2)当时,求函数的值域.
18.如图,甲船从A处以每小时30海里的速度沿正北方向航行,乙船在B处沿固定方向匀速航行,B在A北偏西105°方向且与A相距10海里处.当甲船航行20分钟到达C处时,乙船航行到甲船的北偏西120°方向的D处,此时两船相距10海里.
(1)求乙船每小时航行多少海里?
(2)在C处北偏西30°方向且与C相距海里处有一个暗礁E,暗礁E周围海里范围内为航行危险区域.问:甲、乙两船按原航向和速度航行有无危险?如有危险,从有危险开始多少小时后能脱离危险;如无危险,请说明理由.
19.为弘扬劳动精神,树立学生“劳动最美,劳动最光荣”的观念,某校持续开展“家庭劳动大比拼”活动.某班统计了本班同学1~7月份的人均月劳动时间(单位:小时),并建立了人均月劳动时间y关于月份x的线性回归方程,y与x的原始数据如表所示:
月份x 1 2 3 4 5 6 7
人均月劳动时间y 8 9 m 12 n 19 22
由于某些原因导致部分数据丢失,但已知.
(1)求m,n的值;
(2)求该班6月份人均月劳动时间数据的残差值(残差即样本数据与预测值之差).
参考公式:在线性回归方程中,.
20.学校举办运动会,某班有人报名参赛,其中人报名参加游泳比赛,人报名参加田径比赛,人报名参加球类比赛,同时报名参加游泳比赛和田径比赛的有人,同时报名参加田径比赛和球类比赛的有人,没有人同时报名参加这三项比赛.
(1)求同时报名参加游泳和球类比赛的学生人数;
(2)在只报名参加游泳一项比赛的人中,男生比女生多人,且男生甲和女生乙都在其中,现从这人中随机选出男女生各人,求男生甲被选中且女生乙未被选中的概率.
21.已知函数.
(1)当时,求曲线在点,处的切线方程;
(2)若存在,,使得不等式成立,求的取值范围.
22.在直角坐标系xOy中,以O为极点,x轴非负半轴为极轴,取相同单位长度,建立极坐标系.曲线C的极坐标方程为,M,N分别为C与x轴、y轴的交点.
(1)写出C的直角坐标方程,并求M,N的极坐标;
(2)设MN的中点为P,求直线OP的极坐标方程.
23.已知(,).
(1)当,时,解关于的不等式;
(2)若最小值为,求的最小值.
参考答案
1.A 2.A 3.B 4.D 5.A 6.B 7.D 8.D 9.B 10.A 11.C 12.D 13.60
14.7
15.
16.
17.(1),;(2).
18.(1)每小时30海里;(2)甲船没有危险,乙船有危险,且在遭遇危险开始持续小时后脱险,理由见解析.
19.(1)m=10,n=16;(2).
20.
(1)
(2)
21.(1);(2).
22.(1)见解析;(2)见解析
23.
(1)
(2)
同课章节目录
