2021-2022学年苏科版数学八年级下册第10章分式达标检测卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级下册第10章分式达标检测卷(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 77.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 19:04:25 | ||
图片预览
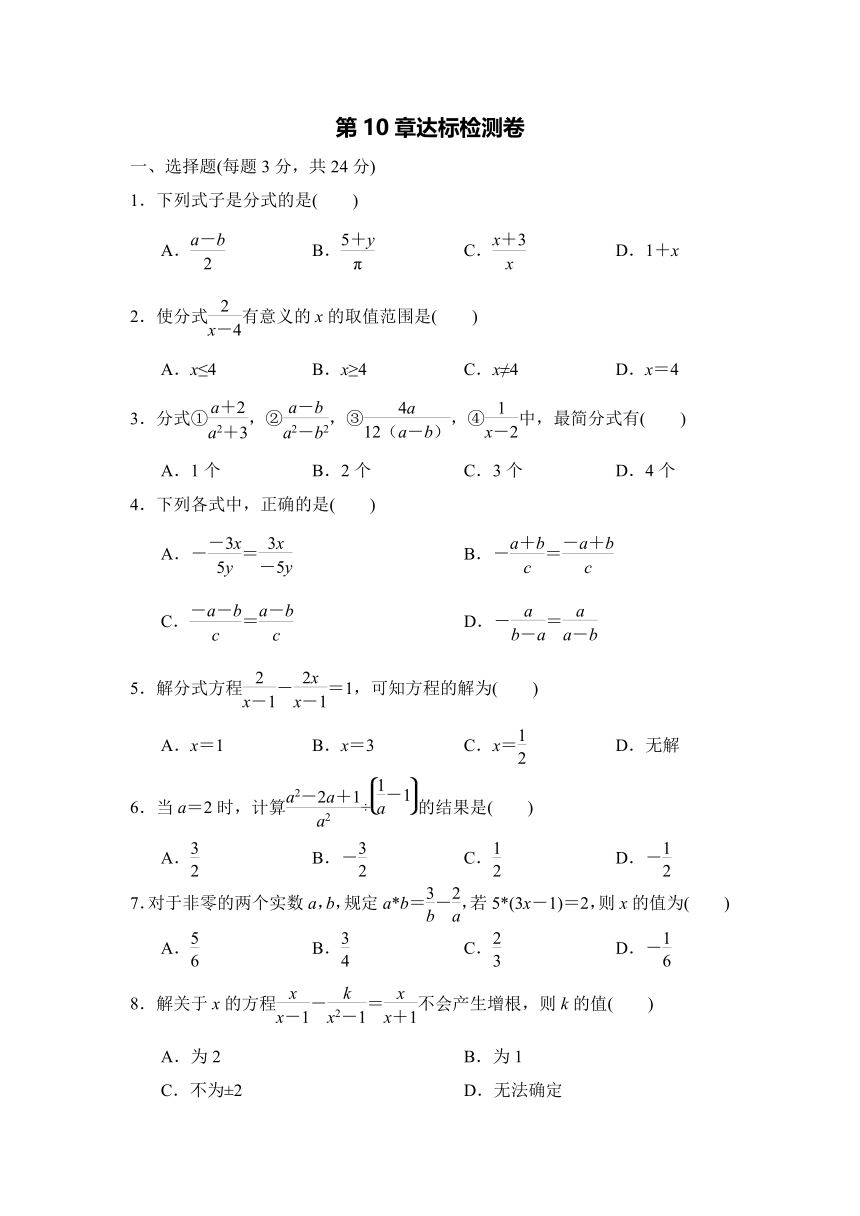

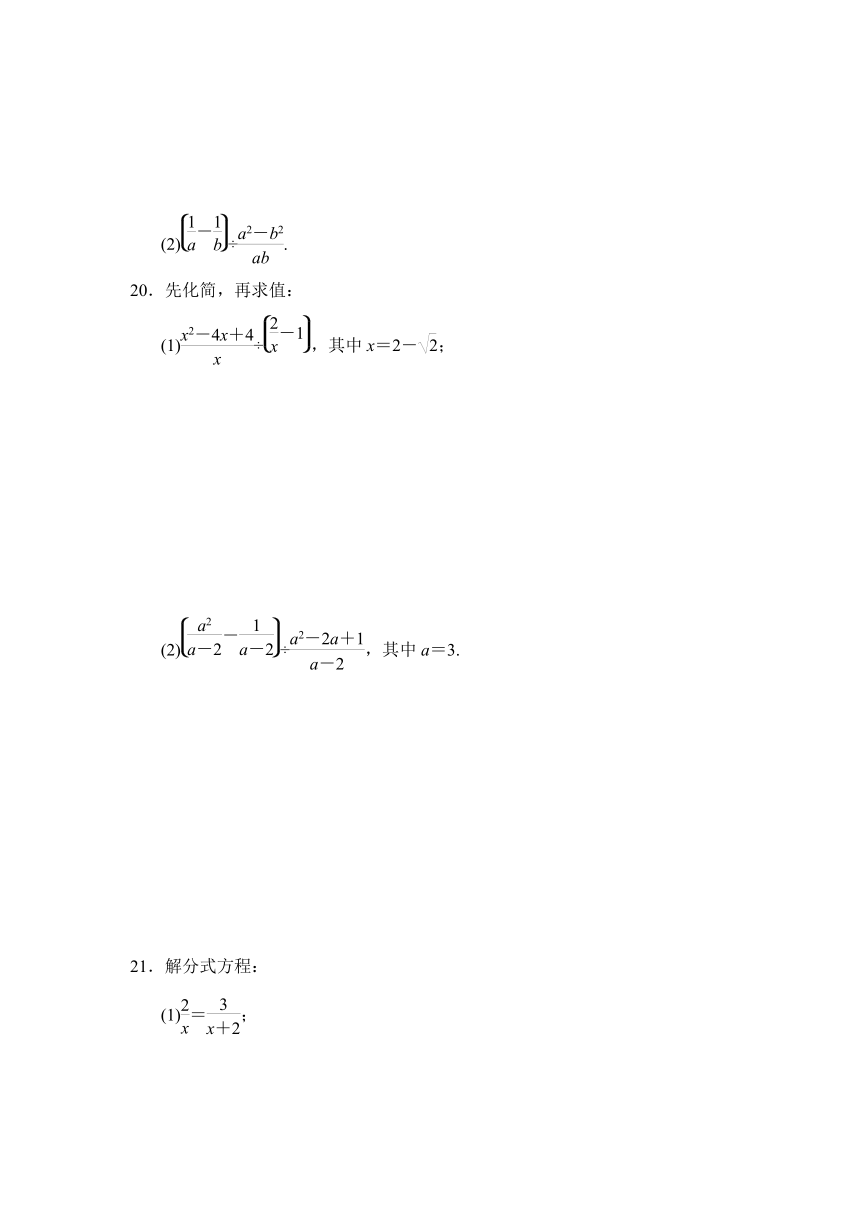


文档简介
第10章达标检测卷
一、选择题(每题3分,共24分)
1.下列式子是分式的是( )
A. B. C. D.1+x
2.使分式有意义的x的取值范围是( )
A.x≤4 B.x≥4 C.x≠4 D.x=4
3.分式①,②,③,④中,最简分式有( )
A.1个 B.2个 C.3个 D.4个
4.下列各式中,正确的是( )
A.-= B.-=
C.= D.-=
5.解分式方程-=1,可知方程的解为( )
A.x=1 B.x=3 C.x= D.无解
6.当a=2时,计算÷的结果是( )
A. B.- C. D.-
7.对于非零的两个实数a,b,规定a*b=-,若5*(3x-1)=2,则x的值为( )
A. B. C. D.-
8.解关于x的方程-=不会产生增根,则k的值( )
A.为2 B.为1
C.不为±2 D.无法确定
二、填空题(每题2分,共20分)
9.与的最简公分母是________.
10.计算·÷的结果是________.
11.若x=1是分式方程-=0的根,则a=________.
12.若关于x的方程-1=0无实数根,则a的值为________.
13.若关于x的分式方程+=1的解为正数,则m的取值范围是________.
14.小明同学在对分式方程+=1去分母时,方程右边的1没有乘x-2,若此时解得x=2,则原方程的解为________.
15.已知=+,则A=________,B=________.
16.目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小琼步行12 000步与小博步行
9 000步消耗的能量相同.若小琼每消耗1千卡能量行走的步数比小博的多10步,则小博每消耗1千卡能量需要行走________步.
17.若=3,则+=________.
18.“绿水青山就是金山银山”.某地为美化环境,计划种植树木6 000棵.由于志愿者的加入,实际每天植树的棵数比原计划增加了25%,结果提前3天完成任务,则实际每天植树________棵.
三、解答题(19~21题每题6分,22~23题每题7分,24~26题每题8分,共56分)
19.计算:(1)-;
(2)÷.
20.先化简,再求值:
(1)÷,其中x=2-;
(2)÷,其中a=3.
21.解分式方程:
(1)=;
(2)+=1.
22.已知M=,N=,用“+”或“-”连接M,N,有三种不同的形式:M+N,M-N,N-M,任选其中一种进行计算,并化简求值,其中
x∶ y=5∶ 2.
23.已知关于x的方程-=.
(1)若m=-3,解这个方程;
(2)若原方程无解,求m的值.
24.为落实节约用水的政策,某旅游景点进行设施改造,将手拧水龙头全部更换成感应水龙头.已知该景点在设施改造后,平均每天用水量是原来的一半,20吨水可以比原来多用5天.该景点在设施改造后平均每天用水多少吨?
25.小张去离家2 520 m的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有23 min,于是他跑步回家,拿到门票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小张骑车的时间比跑步的时间少用了4 min,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度.
(2)如果小张在家取票和寻找“共享单车”共用了5 min,他能否在演唱会开始前赶到奥体中心?并说明理由.
26.阅读下面材料,解答后面的问题.
解方程:-=0.
解:设y=,则原方程可化为y-=0,方程两边同时乘y,得y2-4=0,解得y=±2.
经检验,y=2和y=-2都是方程y-=0的解.
当y=2时,=2,解得x=-1;
当y=-2时,=-2,解得x=.
经检验,x=-1和x=都是原分式方程的解.∴原分式方程的解为x=-1或x=.
上述这种解分式方程的方法称为换元法.
问题:
(1)若在方程-=0中,设y=,则原方程可化为______________;
(2)若在方程-=0中,设y=,则原方程可化为_____________;
(3)模仿上述换元法解方程:--1=0.
答案
一、1.C 2.C 3.B 4.D 5.D 6.D
7.B 点拨:根据题意得-=2,解得x=.经检验x=是原方程的解.故选B.
8.C 点拨:去分母,得x(x+1)-k=x(x-1),解得x=k.∵方程-=不会产生增根,∴x≠±1,∴k≠±1,即k≠±2.故选C.
二、9.18a2b2c 10.-x2
11.1 点拨:∵x=1是分式方程-=0的根,∴-=0,解得a=1.
12.1或-1 13.m>2且m≠3
14.x=1 点拨:小明去分母得到的整式方程是2x-(3-m)=1,把x=2代入,得4-(3-m)=1,解得3-m=3.故原分式方程为+=1,解得x=1,经检验,x=1是原分式方程的解.
15.-; 点拨:∵=+,
∴==,
∴解得
16.30 点拨:设小博每消耗1千卡能量需要行走x步,则小琼每消耗1千卡能量需要行走(x+10)步,根据题意得=,解得x=30,经检验,
x=30是原方程的解.故小博每消耗1千卡能量需要行走30步.
17. 18.500
三、19.解:(1)原式=-=.
(2)原式=·=-·=-.
20.解:(1)原式=÷=·=2-x.当x=2-时,
原式=2-(2-)=.
(2)原式=·=·=.当a=3时,原式==2.
21.解:(1)方程两边都乘x(x+2),
得2(x+2)=3x,解得x=4.
检验:当x=4时,x(x+2)≠0,
所以原分式方程的解为x=4.
(2)方程两边都乘(x+1)(x-1),得(x+1)2+4=(x+1)(x-1),解得x=-3.
检验:当x=-3时,(x+1)(x-1)≠0,所以原分式方程的解为x=-3.
22.解:选择一,M+N=+==.当x∶y=5∶2时,x=y,∴原式==;
选择二,M-N=-==.当x∶y=5∶2时,x=y,∴原式==-;
选择三,N-M=-==.当x∶y=5∶2时,x=y,∴原式==.
点拨:任选一种即可.
23.解:(1)把m=-3代入原方程得-=.
方程两边都乘(x-3)(x+3),得-3(x-3)+(x+3)=1.
解这个一元一次方程,得x=5.5.
检验:当x=5.5时,(x+3)(x-3)≠0,
∴x=5.5是原方程的解.
(2)当(x+3)(x-3)=0时,x=±3.
方程两边都乘(x-3)(x+3),得m(x-3)+(x+3)=m+4,
整理,得(m+1)x=1+4m,
当m+1=0时,1+4m≠0,方程无解,此时m=-1.当m+1≠0时,x=,当x=3时,(x-3)(x+3)=0,方程无解,即=3,解得m=2.当x=-3时,(x-3)(x+3)=0,方程无解,即=-3,解得m=-.
综上,若原方程无解,则m=-1或2或-.
24.解:设该景点在设施改造后平均每天用水x吨,则在改造前平均每天用水2x吨,
根据题意,得-=5,
解得x=2.
经检验,x=2是原方程的解,且符合题意.
答:该景点在设施改造后平均每天用水2吨.
25.解:(1)设小张跑步的平均速度为x m/min,则小张骑车的平均速度为
1.5x m/min,
根据题意,得-=4,
解得x=210.
经检验,x=210是原方程的解,且符合题意.
答:小张跑步的平均速度为210 m/min.
(2)不能.理由:小张跑步到家所用时间为2 520÷210=12(min),
小张骑车赶回奥体中心所用时间为12-4=8(min),
小张从开始跑步回家到赶回奥体中心所用时间为12+8+5=25(min),
∵25>23,
∴小张不能在演唱会开始前赶到奥体中心.
26.解:(1)-=0 (2)y-=0
(3)原方程可化为-=0,
设y=,
则原方程可化为y-=0,
方程两边同时乘y,得y2-1=0,解得y=±1.
经检验,y=1和y=-1都是方程y-=0的解.
当y=1时,=1,该方程无解;
当y=-1时,=-1,解得x=-.经检验,x=-是原分式方程的解.
∴原分式方程的解为x=-.
一、选择题(每题3分,共24分)
1.下列式子是分式的是( )
A. B. C. D.1+x
2.使分式有意义的x的取值范围是( )
A.x≤4 B.x≥4 C.x≠4 D.x=4
3.分式①,②,③,④中,最简分式有( )
A.1个 B.2个 C.3个 D.4个
4.下列各式中,正确的是( )
A.-= B.-=
C.= D.-=
5.解分式方程-=1,可知方程的解为( )
A.x=1 B.x=3 C.x= D.无解
6.当a=2时,计算÷的结果是( )
A. B.- C. D.-
7.对于非零的两个实数a,b,规定a*b=-,若5*(3x-1)=2,则x的值为( )
A. B. C. D.-
8.解关于x的方程-=不会产生增根,则k的值( )
A.为2 B.为1
C.不为±2 D.无法确定
二、填空题(每题2分,共20分)
9.与的最简公分母是________.
10.计算·÷的结果是________.
11.若x=1是分式方程-=0的根,则a=________.
12.若关于x的方程-1=0无实数根,则a的值为________.
13.若关于x的分式方程+=1的解为正数,则m的取值范围是________.
14.小明同学在对分式方程+=1去分母时,方程右边的1没有乘x-2,若此时解得x=2,则原方程的解为________.
15.已知=+,则A=________,B=________.
16.目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现小琼步行12 000步与小博步行
9 000步消耗的能量相同.若小琼每消耗1千卡能量行走的步数比小博的多10步,则小博每消耗1千卡能量需要行走________步.
17.若=3,则+=________.
18.“绿水青山就是金山银山”.某地为美化环境,计划种植树木6 000棵.由于志愿者的加入,实际每天植树的棵数比原计划增加了25%,结果提前3天完成任务,则实际每天植树________棵.
三、解答题(19~21题每题6分,22~23题每题7分,24~26题每题8分,共56分)
19.计算:(1)-;
(2)÷.
20.先化简,再求值:
(1)÷,其中x=2-;
(2)÷,其中a=3.
21.解分式方程:
(1)=;
(2)+=1.
22.已知M=,N=,用“+”或“-”连接M,N,有三种不同的形式:M+N,M-N,N-M,任选其中一种进行计算,并化简求值,其中
x∶ y=5∶ 2.
23.已知关于x的方程-=.
(1)若m=-3,解这个方程;
(2)若原方程无解,求m的值.
24.为落实节约用水的政策,某旅游景点进行设施改造,将手拧水龙头全部更换成感应水龙头.已知该景点在设施改造后,平均每天用水量是原来的一半,20吨水可以比原来多用5天.该景点在设施改造后平均每天用水多少吨?
25.小张去离家2 520 m的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有23 min,于是他跑步回家,拿到门票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小张骑车的时间比跑步的时间少用了4 min,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度.
(2)如果小张在家取票和寻找“共享单车”共用了5 min,他能否在演唱会开始前赶到奥体中心?并说明理由.
26.阅读下面材料,解答后面的问题.
解方程:-=0.
解:设y=,则原方程可化为y-=0,方程两边同时乘y,得y2-4=0,解得y=±2.
经检验,y=2和y=-2都是方程y-=0的解.
当y=2时,=2,解得x=-1;
当y=-2时,=-2,解得x=.
经检验,x=-1和x=都是原分式方程的解.∴原分式方程的解为x=-1或x=.
上述这种解分式方程的方法称为换元法.
问题:
(1)若在方程-=0中,设y=,则原方程可化为______________;
(2)若在方程-=0中,设y=,则原方程可化为_____________;
(3)模仿上述换元法解方程:--1=0.
答案
一、1.C 2.C 3.B 4.D 5.D 6.D
7.B 点拨:根据题意得-=2,解得x=.经检验x=是原方程的解.故选B.
8.C 点拨:去分母,得x(x+1)-k=x(x-1),解得x=k.∵方程-=不会产生增根,∴x≠±1,∴k≠±1,即k≠±2.故选C.
二、9.18a2b2c 10.-x2
11.1 点拨:∵x=1是分式方程-=0的根,∴-=0,解得a=1.
12.1或-1 13.m>2且m≠3
14.x=1 点拨:小明去分母得到的整式方程是2x-(3-m)=1,把x=2代入,得4-(3-m)=1,解得3-m=3.故原分式方程为+=1,解得x=1,经检验,x=1是原分式方程的解.
15.-; 点拨:∵=+,
∴==,
∴解得
16.30 点拨:设小博每消耗1千卡能量需要行走x步,则小琼每消耗1千卡能量需要行走(x+10)步,根据题意得=,解得x=30,经检验,
x=30是原方程的解.故小博每消耗1千卡能量需要行走30步.
17. 18.500
三、19.解:(1)原式=-=.
(2)原式=·=-·=-.
20.解:(1)原式=÷=·=2-x.当x=2-时,
原式=2-(2-)=.
(2)原式=·=·=.当a=3时,原式==2.
21.解:(1)方程两边都乘x(x+2),
得2(x+2)=3x,解得x=4.
检验:当x=4时,x(x+2)≠0,
所以原分式方程的解为x=4.
(2)方程两边都乘(x+1)(x-1),得(x+1)2+4=(x+1)(x-1),解得x=-3.
检验:当x=-3时,(x+1)(x-1)≠0,所以原分式方程的解为x=-3.
22.解:选择一,M+N=+==.当x∶y=5∶2时,x=y,∴原式==;
选择二,M-N=-==.当x∶y=5∶2时,x=y,∴原式==-;
选择三,N-M=-==.当x∶y=5∶2时,x=y,∴原式==.
点拨:任选一种即可.
23.解:(1)把m=-3代入原方程得-=.
方程两边都乘(x-3)(x+3),得-3(x-3)+(x+3)=1.
解这个一元一次方程,得x=5.5.
检验:当x=5.5时,(x+3)(x-3)≠0,
∴x=5.5是原方程的解.
(2)当(x+3)(x-3)=0时,x=±3.
方程两边都乘(x-3)(x+3),得m(x-3)+(x+3)=m+4,
整理,得(m+1)x=1+4m,
当m+1=0时,1+4m≠0,方程无解,此时m=-1.当m+1≠0时,x=,当x=3时,(x-3)(x+3)=0,方程无解,即=3,解得m=2.当x=-3时,(x-3)(x+3)=0,方程无解,即=-3,解得m=-.
综上,若原方程无解,则m=-1或2或-.
24.解:设该景点在设施改造后平均每天用水x吨,则在改造前平均每天用水2x吨,
根据题意,得-=5,
解得x=2.
经检验,x=2是原方程的解,且符合题意.
答:该景点在设施改造后平均每天用水2吨.
25.解:(1)设小张跑步的平均速度为x m/min,则小张骑车的平均速度为
1.5x m/min,
根据题意,得-=4,
解得x=210.
经检验,x=210是原方程的解,且符合题意.
答:小张跑步的平均速度为210 m/min.
(2)不能.理由:小张跑步到家所用时间为2 520÷210=12(min),
小张骑车赶回奥体中心所用时间为12-4=8(min),
小张从开始跑步回家到赶回奥体中心所用时间为12+8+5=25(min),
∵25>23,
∴小张不能在演唱会开始前赶到奥体中心.
26.解:(1)-=0 (2)y-=0
(3)原方程可化为-=0,
设y=,
则原方程可化为y-=0,
方程两边同时乘y,得y2-1=0,解得y=±1.
经检验,y=1和y=-1都是方程y-=0的解.
当y=1时,=1,该方程无解;
当y=-1时,=-1,解得x=-.经检验,x=-是原分式方程的解.
∴原分式方程的解为x=-.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
