2021-2022学年苏科版数学八年级下册第12章 二次根式达标检测卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版数学八年级下册第12章 二次根式达标检测卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 94.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 00:00:00 | ||
图片预览


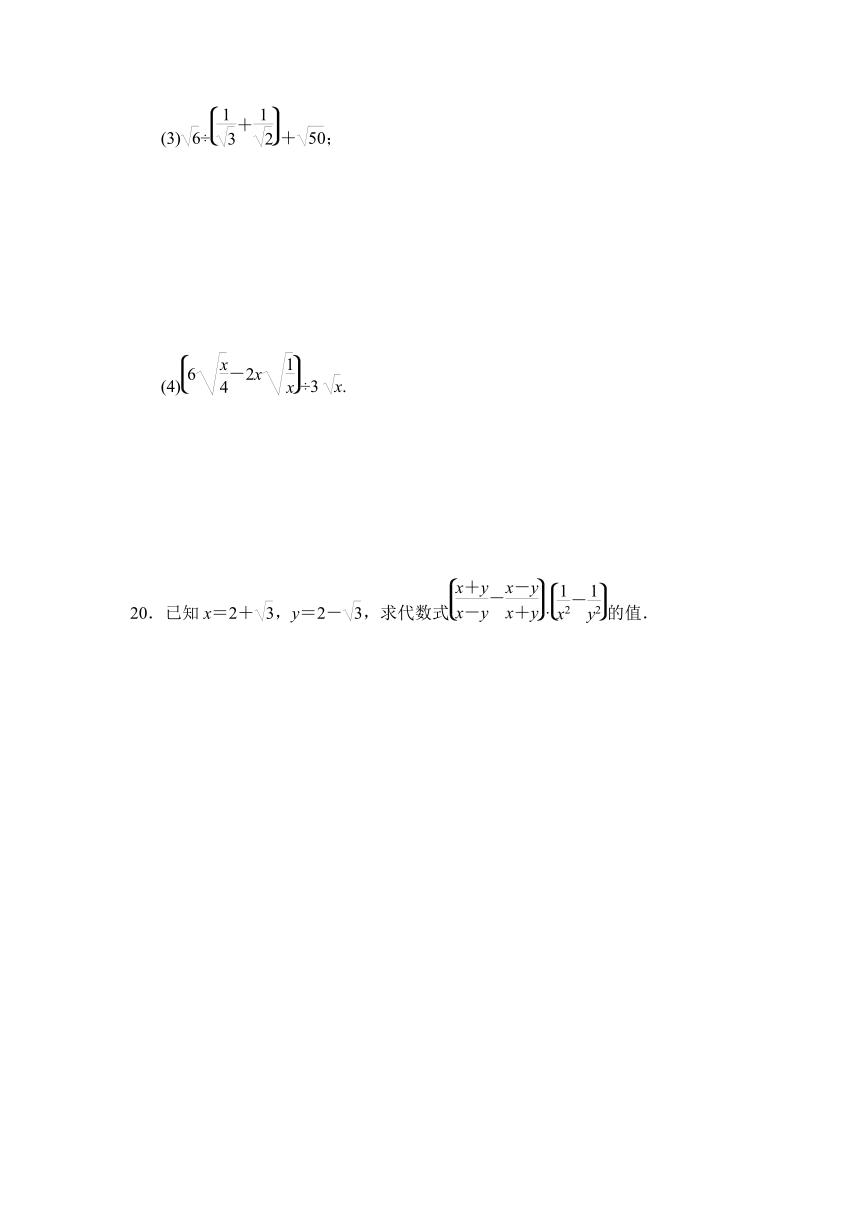

文档简介
第12章达标检测卷
一、选择题(每题3分,共24分)
1.若二次根式在实数范围内有意义,则x的取值范围是( )
A.x≥4 B.x≥-4 C.x≤-4 D.x>4
2.若为二次根式,则m的取值范围是( )
A.m<3 B.m≤3 C.m≥3 D.m>3
3.下列等式成立的是( )
A.=±4 B.=2
C.-a= D.-=-8
4.计算()2的结果是( )
A. B.3 C.2 D.9
5.下列计算正确的是( )
A.+= B.3+=3
C.×= D.2 -2=
6.等式=成立的条件是( )
A.x> B.x≥
C.x>2 D.≤x<2
7.计算+的结果是( )
A.65 B.5 C.5 D.5
8.计算-×的结果是( )
A.0 B. C.3 D.
二、填空题(每题2分,共20分)
9.计算:-=________.
10.若最简二次根式与可以合并,则a=________.
11.计算(+1)(-1)的结果等于________.
12.计算:2÷5 ×=________.
13.若有意义,则x的取值范围是________.
14.不等式2x->0的解集是________.
15.如果菱形的两条对角线长分别为(+)cm和(-)cm,那么菱形的面积为________.
16.已知a=2-,则代数式a2-4a-2的值为________.
17.已知y=-x+5,当x分别取1,2,3,…,2 022时,所对应y值的总和是________.
18.若计算×m的结果为正整数,则无理数m的值可以是________________(写出一个符合条件的即可).
三、解答题(19,24题每题8分,20~23题每题5分,25~26题每题10分,共56分)
19.计算:(1)3 ÷(-2)·(a>0);
(2)+4-+3;
(3)÷+;
(4)÷3 .
20.已知x=2+,y=2-,求代数式·的值.
21.嘉琪准备完成题目“计算:-”时,发现“■”处的数字印刷不清楚,她把“■”处的数学猜成3,请你计算-.
22.已知a、b分别为等腰三角形的两条边长,且a、b满足b=4++3,求此三角形的周长.
23.已知等腰三角形的腰长为2 cm,底边长为4 cm,求这个等腰三角形的面积.
24.已知+=×.
(1)求a+b的值;
(2)求7x+y2 022的值.
25.细心观察下图,认真分析各点,然后回答问题.
OA22=()2+1=2,S1=;OA32=()2+1=3,S2= ;
OA42=()2+1=4,S3=;….
(1)请用含n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求出S12+S22+S32+…+S102的值.
26.阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2=(1+)2,善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为正整数),则有a+b=m2+2n2+2mn,
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b=(m+n)2,用含m、n的式子分别表示a、b,得a=________,b=________;
(2)若a+4=(m+n)2,且a、m、n均为正整数,求a的值;
(3)化简:.
答案
一、1.A 2.B 3.D 4.B 5.C
6.C 7.C 8.B
二、9. 10.1 11.6 12.
13.x≥1且x≠2
14.x> 15.1cm2 16.-1 17.2 034
18.(答案不唯一)
三、19.解:(1)原式=-×=-×=-.
(2)原式=2+4×-×3+3×=2+2-2+=3.
(3)原式=÷+5=÷+5=×+
5=×+5=3·-2·+5=6-
6+5=6-.
(4)原式=÷3 =÷3=
20.解:原式=-.
当x=2+,y=2-时,原式=-4.
21.解:-(-4)=3×-×3-+4×=-2-+2=-.
22.解:由题意得3a-6≥0,2-a≥0,解得a≥2,a≤2,∴a=2,∴b=4,
∵2+2=4,∴2、2、4不能组成三角形,
∴此三角形的三边长分别为2、4、4.
∴此三角形的周长为2+4+4=10.
23.解:此等腰三角形底边上的高为=4(cm),所以三角形的面积=×4×4=8(cm2).
24.解:(1)由题意可知:
解得:a+b=2 022.
(2)由(1)易知×=0,
∴
解得
∴7x+y2 022=14+1=15.
25.解:(1)OAn2=()2+1=n,
Sn=.
(2)因为OA1=1,OA2=,OA3=,所以OA10=.
(3)S12+S22+S32+…+S102=+++…+=×(1+2+3+…+10)=.
26.解:(1)m2+6n2;2mn
(2)∵(m+n)2=m2+3n2+2mn,a+4=(m+n)2,
∴a=m2+3n2,mn=2.
∵m、n均为正整数,
∴m=1,n=2或m=2,n=1,
∴a=13或7.
(3)===2 +1,
则====-1.
一、选择题(每题3分,共24分)
1.若二次根式在实数范围内有意义,则x的取值范围是( )
A.x≥4 B.x≥-4 C.x≤-4 D.x>4
2.若为二次根式,则m的取值范围是( )
A.m<3 B.m≤3 C.m≥3 D.m>3
3.下列等式成立的是( )
A.=±4 B.=2
C.-a= D.-=-8
4.计算()2的结果是( )
A. B.3 C.2 D.9
5.下列计算正确的是( )
A.+= B.3+=3
C.×= D.2 -2=
6.等式=成立的条件是( )
A.x> B.x≥
C.x>2 D.≤x<2
7.计算+的结果是( )
A.65 B.5 C.5 D.5
8.计算-×的结果是( )
A.0 B. C.3 D.
二、填空题(每题2分,共20分)
9.计算:-=________.
10.若最简二次根式与可以合并,则a=________.
11.计算(+1)(-1)的结果等于________.
12.计算:2÷5 ×=________.
13.若有意义,则x的取值范围是________.
14.不等式2x->0的解集是________.
15.如果菱形的两条对角线长分别为(+)cm和(-)cm,那么菱形的面积为________.
16.已知a=2-,则代数式a2-4a-2的值为________.
17.已知y=-x+5,当x分别取1,2,3,…,2 022时,所对应y值的总和是________.
18.若计算×m的结果为正整数,则无理数m的值可以是________________(写出一个符合条件的即可).
三、解答题(19,24题每题8分,20~23题每题5分,25~26题每题10分,共56分)
19.计算:(1)3 ÷(-2)·(a>0);
(2)+4-+3;
(3)÷+;
(4)÷3 .
20.已知x=2+,y=2-,求代数式·的值.
21.嘉琪准备完成题目“计算:-”时,发现“■”处的数字印刷不清楚,她把“■”处的数学猜成3,请你计算-.
22.已知a、b分别为等腰三角形的两条边长,且a、b满足b=4++3,求此三角形的周长.
23.已知等腰三角形的腰长为2 cm,底边长为4 cm,求这个等腰三角形的面积.
24.已知+=×.
(1)求a+b的值;
(2)求7x+y2 022的值.
25.细心观察下图,认真分析各点,然后回答问题.
OA22=()2+1=2,S1=;OA32=()2+1=3,S2= ;
OA42=()2+1=4,S3=;….
(1)请用含n(n是正整数)的等式表示上述变化规律;
(2)推算出OA10的长;
(3)求出S12+S22+S32+…+S102的值.
26.阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2=(1+)2,善于思考的小明进行了以下探索:
设a+b=(m+n)2(其中a、b、m、n均为正整数),则有a+b=m2+2n2+2mn,
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b=(m+n)2,用含m、n的式子分别表示a、b,得a=________,b=________;
(2)若a+4=(m+n)2,且a、m、n均为正整数,求a的值;
(3)化简:.
答案
一、1.A 2.B 3.D 4.B 5.C
6.C 7.C 8.B
二、9. 10.1 11.6 12.
13.x≥1且x≠2
14.x> 15.1cm2 16.-1 17.2 034
18.(答案不唯一)
三、19.解:(1)原式=-×=-×=-.
(2)原式=2+4×-×3+3×=2+2-2+=3.
(3)原式=÷+5=÷+5=×+
5=×+5=3·-2·+5=6-
6+5=6-.
(4)原式=÷3 =÷3=
20.解:原式=-.
当x=2+,y=2-时,原式=-4.
21.解:-(-4)=3×-×3-+4×=-2-+2=-.
22.解:由题意得3a-6≥0,2-a≥0,解得a≥2,a≤2,∴a=2,∴b=4,
∵2+2=4,∴2、2、4不能组成三角形,
∴此三角形的三边长分别为2、4、4.
∴此三角形的周长为2+4+4=10.
23.解:此等腰三角形底边上的高为=4(cm),所以三角形的面积=×4×4=8(cm2).
24.解:(1)由题意可知:
解得:a+b=2 022.
(2)由(1)易知×=0,
∴
解得
∴7x+y2 022=14+1=15.
25.解:(1)OAn2=()2+1=n,
Sn=.
(2)因为OA1=1,OA2=,OA3=,所以OA10=.
(3)S12+S22+S32+…+S102=+++…+=×(1+2+3+…+10)=.
26.解:(1)m2+6n2;2mn
(2)∵(m+n)2=m2+3n2+2mn,a+4=(m+n)2,
∴a=m2+3n2,mn=2.
∵m、n均为正整数,
∴m=1,n=2或m=2,n=1,
∴a=13或7.
(3)===2 +1,
则====-1.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
