北师大版八上数学期末复习专题一次函数压轴题专练(word解析版)
文档属性
| 名称 | 北师大版八上数学期末复习专题一次函数压轴题专练(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 07:38:02 | ||
图片预览



文档简介
一次函数压轴题专练
1.(2021秋 海珠区校级期中)如图所示,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足,C的坐标为(﹣1,0),且AH⊥BC于点H,AH交OB于点P.
(1)如图1,写出a、b的值,证明△AOP≌△BOC;
(2)如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,求证:S△BDM﹣S△ADN=4.
2.(2021秋 高新区校级期中)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求出点A、点B的坐标;
(2)求△COB的面积;
(3)在y轴上是否存在一点P,使得△PBC为等腰三角形?若存在,请直接写出点P坐标,若不存在,请说明理由.
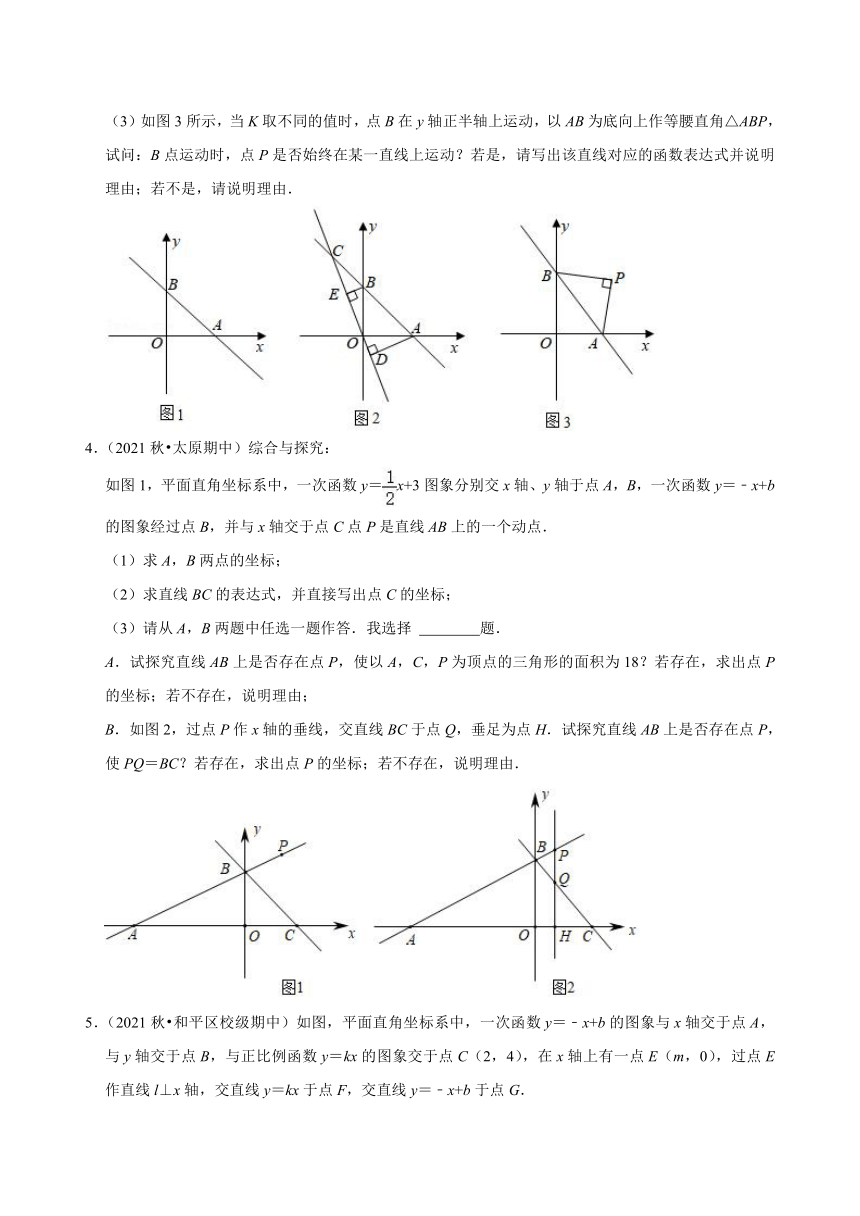
3.(2021秋 苏家屯区期中)如图1所示,直线l:y=k(x﹣2)(k<0)与x轴正半轴和y轴正半轴分别交于点A、B两点.
(1)当OA=OB时,求直线l的表达式;
(2)在(1)的条件下,如图2所示,设C为线段AB延长线上一点,作直线OC,过点A、B两点分别作AD⊥OC于点D,BE⊥OC于点E,若AD=,求BE的长;
(3)如图3所示,当K取不同的值时,点B在y轴正半轴上运动,以AB为底向上作等腰直角△ABP,试问:B点运动时,点P是否始终在某一直线上运动?若是,请写出该直线对应的函数表达式并说明理由;若不是,请说明理由.
4.(2021秋 太原期中)综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
(3)请从A,B两题中任选一题作答.我选择 题.
A.试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由;
B.如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
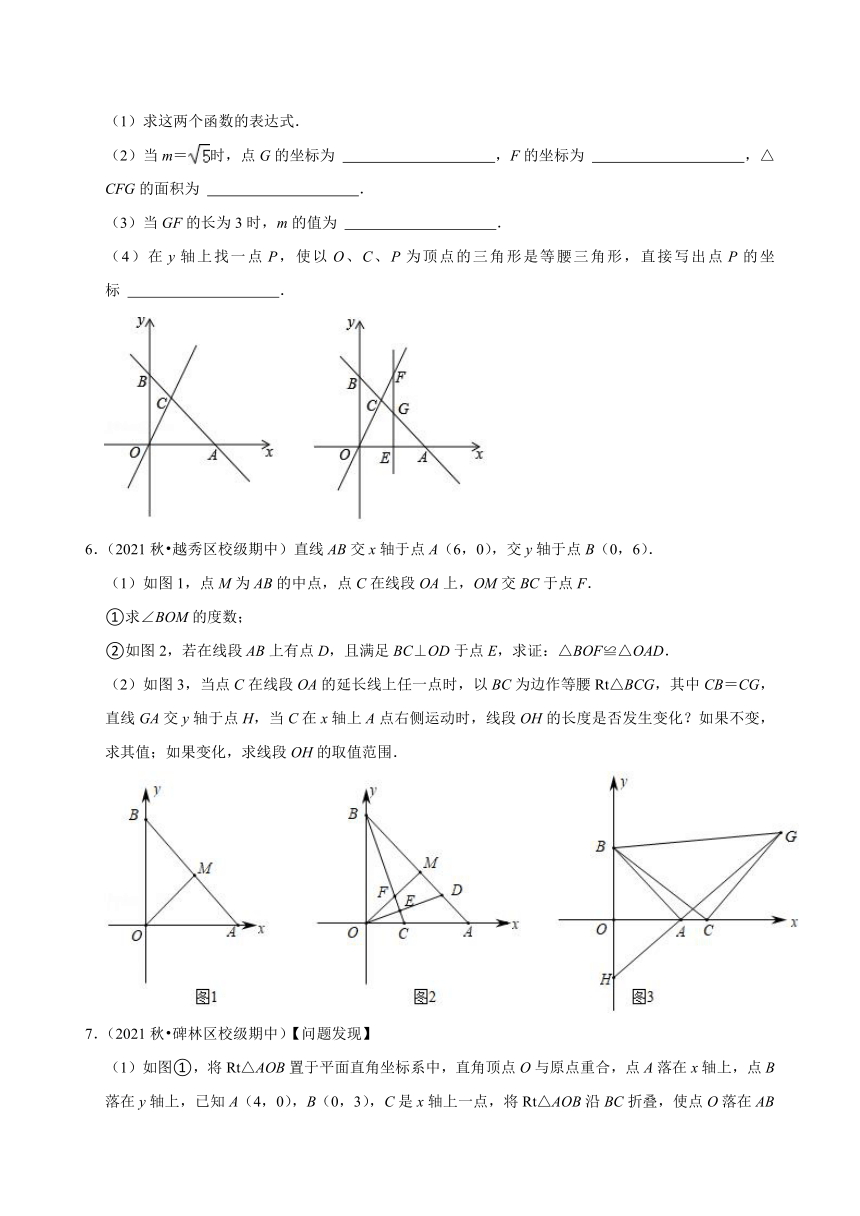
5.(2021秋 和平区校级期中)如图,平面直角坐标系中,一次函数y=﹣x+b的图象与x轴交于点A,与y轴交于点B,与正比例函数y=kx的图象交于点C(2,4),在x轴上有一点E(m,0),过点E作直线l⊥x轴,交直线y=kx于点F,交直线y=﹣x+b于点G.
(1)求这两个函数的表达式.
(2)当m=时,点G的坐标为 ,F的坐标为 ,△CFG的面积为 .
(3)当GF的长为3时,m的值为 .
(4)在y轴上找一点P,使以O、C、P为顶点的三角形是等腰三角形,直接写出点P的坐标 .
6.(2021秋 越秀区校级期中)直线AB交x轴于点A(6,0),交y轴于点B(0,6).
(1)如图1,点M为AB的中点,点C在线段OA上,OM交BC于点F.
①求∠BOM的度数;
②如图2,若在线段AB上有点D,且满足BC⊥OD于点E,求证:△BOF≌△OAD.
(2)如图3,当点C在线段OA的延长线上任一点时,以BC为边作等腰Rt△BCG,其中CB=CG,直线GA交y轴于点H,当C在x轴上A点右侧运动时,线段OH的长度是否发生变化?如果不变,求其值;如果变化,求线段OH的取值范围.
7.(2021秋 碑林区校级期中)【问题发现】
(1)如图①,将Rt△AOB置于平面直角坐标系中,直角顶点O与原点重合,点A落在x轴上,点B落在y轴上,已知A(4,0),B(0,3),C是x轴上一点,将Rt△AOB沿BC折叠,使点O落在AB边上的点D处,则点C的坐标为 .
【问题探究】
(2)如图②,将长方形OABC置于平面直角坐标系中,点A在y轴上,点C在x轴上,已知B(12,5),E是OA上一点,将长方形OABC沿CE折叠,点O恰好落在对角线AC上的点F处,求OF所在直线的函数表达式.
(3)如图③,将长方形OABC置于平面直角坐标系中,点A在y轴上,点C在x轴上,已知B(8,6),D在对角线AC上,且CD=OC,P是OD的中点,Q是OC上一点,将△OPQ沿PQ折叠,使点O落在AC边上的点E处,求点D的坐标及四边形OPEQ的面积.
8.(2021秋 和平区期中)如图1,直线y=x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)直线BC的函数表达式为 ;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,请直接写出点P的坐标 ;
②若△PQB的面积为,请直接写出点M的坐标 ;
③若点K为线段OB的中点,连接CK,如图2,若在线段OC上有一点F,满足∠CKF=45°,请直接写出点F的坐标 .
9.(2021秋 碑林区校级期中)如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MN∥x轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
10.(2021秋 深圳期中)如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)填空:k= ;b= ;m= ;
(2)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由.
(3)若动点P在射线DC上从点D开始以每秒1个单位的速度运动,连接AP,设点P的运动时间为t秒.是否存在t的值,使△ACP和△ADP的面积比为1:3?若存在,直接写出t的值;若不存在,请说明理由.
11.(2021秋 开福区校级月考)已知直线AB交x轴于点A(a,o),交y轴于点B(0,b),且a、b满足|a+b|+(b﹣4)2=0.
(1)求∠ABO的度数;
(2)如图1,若点C在第一象限,且BE⊥AC于点E,延长BE至点D,使得BD=AC,连接OC、OD、CD,试判断△COD的形状,并说明理由;
(3)如图2,若点C在OB上,点F在AB的延长线上,且AC=CF,△ACP是以AC为直角边的等腰直角三角形,CQ⊥AF于点Q,求的值.
12.(2021 南岗区校级开学)如图,直线y=x+6交x轴于A,交y轴于B,把△AOB绕着点O顺时针旋转,得到△COD,且点D在x轴正半轴上,延长AB交CD于点E.
(1)求直线CD的解析式;
(2)点P为线段DE上一点,连接PA、PB,设点P的横坐标为m,△PAB的面积为S,求S与m的函数解析式;
(3)在(2)的条件下,点Q为OD边上一点,若∠PQC=2∠OCQ,PQ+CQ=PA,求点P的坐标.
13.(2021春 黄陂区期末)如图,直线l1:y=kx﹣2k+1经过定点C,分别交x轴,y轴于A,B两点,直线l2经过O,C两点,点Dl2上.
(1)①直接写出点C的坐标为 ;②求直线l2的解析式;
(2)如图1,若S△BOC=2S△BCD,求点D的坐标;
(3)如图2,直线l3经过D,E(0,﹣)两点,分别交x轴的正半轴、l1于点P,F,若PE=PF,∠EDO=45°,求k的值.
14.(2021春 东港区校级期末)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0),(12,6),直线y=﹣x+b(b>0)与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣x+b(b>0)平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,过点P的直线,与直线BC和x轴分别交于点N、M.问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长,若不存在,请说明理由.
(3)将(1)中的直线沿y轴向下平移a个单位得到新直线l,矩形OABC沿平移后的直线折叠,若点O落在边BC上的F处,CF=9,求出a的值.
15.(2021春 连山区期末)如图,矩形OABC在平面直角坐标系中,OA在x轴负半轴,OC在y轴正半轴,点D在边OC上,连接BD,将△BCD沿BD折叠,得到△BDE,使点E落在矩形OABC内部,过点E作EF⊥AB于F,直线CF交x轴于点M,若点E(﹣3,9),F恰为AB中点.
(1)如图1,直线CM的解析式;
(2)如图2,点P为x轴上的动点,过P作x轴的垂线,分别交直线CM、BD于点N、Q,若NQ=2CD,求点P坐标;
(3)点H为直线BD上动点,若△AEH以AE为直角边的直角三角形,是否存在点H?如果存在,直接写出点H坐标;不存在,请说明理由!
16.(2021春 铁锋区期末)综合与探究.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0)、点B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)直接写出AB的长 ;
(2)点C的坐标 ,点D的坐标 ;
(3)求直线AB的函数表达式;
(4)y轴上是否存在一点P,使得S△PAB=S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.
17.(2021春 集贤县期末)如图1,平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
(1)求点C的坐标及直线AB的表达式;
(2)如图2,在x轴上有一点E,过点E作直线l⊥x轴,交直线y=2x于点F,交直线y=kx+b于点G,若GF的长为3,求点E的坐标;
(3)在y轴上是否存在一点M,使以O、C、M为顶点的三角形是等腰三角形,若存在,直接写出点M的坐标;若不存在,说明理由.
18.(2021春 天心区期末)我们知道一次函数y=mx+n与y=﹣mx+n(m≠0)的图象关于y轴对称,所以我们定义:函数y=mx+n与y=﹣mx+n(m≠0)互为“M”函数.
(1)请直接写出函数y=2x+5的“M”函数;
(2)如果一对“M”函数y=mx+n与y=﹣mx+n(m≠0)的图象交于点A,且与x轴交于B,C两点,如图所示,若∠BAC=90°,且△ABC的面积是8,求这对“M”函数的解析式;
(3)在(2)的条件下,若点D是y轴上的一个动点,当△ABD为等腰三角形时,请求出点D的坐标.
19.(2021春 洪泽区期末)如图,直线y=﹣x+12与x轴交于点A(12,0),与直线OB交于点B(8,4),x轴上一点P从O点出发以每秒2个单位的速度向终点A运动,作PE⊥x轴交OB于E,过E作EF∥x轴且EF=PE,以PE、EF为边作矩形PEFG,设运动时间为t.
(1)当点F落在直线AB上时,求t的值;
(2)在运动过程中,设矩形PEFG与△ABO的重叠部分面积为S,求S与t的关系式,并写出相应的t的取值范围;
(3)矩形PEFG的对角线交于点Q,直接写出PQ+AQ的最小值为 .
参考答案与试题解析
1.(2021秋 海珠区校级期中)如图所示,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足,C的坐标为(﹣1,0),且AH⊥BC于点H,AH交OB于点P.
(1)如图1,写出a、b的值,证明△AOP≌△BOC;
(2)如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,求证:S△BDM﹣S△ADN=4.
【解答】(1)解:∵+(a﹣4)2=0,
∴a+b=0,a﹣4=0,
∴a=4,b=﹣4,
则OA=OB=4.
∵AH⊥BC即∠AHC=90°,∠COB=90°,
∴∠HAC+∠ACH=∠OBC+∠OCB=90°,
∴∠HAC=∠OBC.
在△OAP与△OBC中,
,
∴△OAP≌△OBC(ASA);
(2)证明:过O分别作OM⊥CB于M点,作ON⊥HA于N点.
在四边形OMHN中,∠MON=360°﹣3×90°=90°,
∴∠COM=∠PON=90°﹣∠MOP.
∵△OAP≌△OBC,
∴OC=OP,
在△COM与△PON中,
,
∴△COM≌△PON(AAS),
∴OM=ON.
∵OM⊥CB,ON⊥HA,
∴HO平分∠CHA,
∴∠OHP=∠CHA=45°;
(3)证明:如图:连接OD.
∵∠AOB=90°,OA=OB,D为AB的中点,
∴OD⊥AB,∠BOD=∠AOD=45°,OD=DA=BD,
∴∠OAD=45°,∠MOD=90°+45°=135°,
∴∠DAN=135°=∠MOD.
∵MD⊥ND即∠MDN=90°,
∴∠MDO=∠NDA=90°﹣∠MDA.
在△ODM与△ADN中,
,
∴△ODM≌△ADN(ASA),
∴S△ODM=S△ADN.
∴S△BDM﹣S△ADN=S△BDM﹣S△ODM=S△BOD=S△AOB=×AO BO=××4×4=4.
2.(2021秋 高新区校级期中)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求出点A、点B的坐标;
(2)求△COB的面积;
(3)在y轴上是否存在一点P,使得△PBC为等腰三角形?若存在,请直接写出点P坐标,若不存在,请说明理由.
【解答】解:(1)对于直线l2的解析式为y=﹣x+3,令x=0,得到y=3,
∴B(0,3),
令y=0,得到x=6,
∴A(6,0).
∴点A是坐标为(6,0),点B的坐标为(0,3);
(2)联立y=x,y=﹣x+3并解得:x=2,
∴点C(2,2),
∴S△COB=OB xC=×3×2=3;
(3)存在.
∵点B(0,3),点C(2,2),
∴BC==,
设P(0,y),
①当PC=BC=时,如图,
又∵点C(2,2),
∴PC2=22+(2﹣y)2,
∴()2=22+(2﹣y)2,
∴y=1或3,
∵y=3时,与点B重合,故舍去,
∴点P(0,1);
②当BP=BC=时,如图,
OP=OB+PB=3+,OP′=OB﹣P′B=3﹣,
∴点P(0,3+),(0,3﹣);
③当PB=PC时,如图,
∵PB2=PC2,
∴(3﹣y)2=22+(2﹣y)2,
∴解得:y=,
∴点P(0,),
综上所述:点P坐标为(0,3+),(0,3﹣),(0,1),(0,).
3.(2021秋 苏家屯区期中)如图1所示,直线l:y=k(x﹣2)(k<0)与x轴正半轴和y轴正半轴分别交于点A、B两点.
(1)当OA=OB时,求直线l的表达式;
(2)在(1)的条件下,如图2所示,设C为线段AB延长线上一点,作直线OC,过点A、B两点分别作AD⊥OC于点D,BE⊥OC于点E,若AD=,求BE的长;
(3)如图3所示,当K取不同的值时,点B在y轴正半轴上运动,以AB为底向上作等腰直角△ABP,试问:B点运动时,点P是否始终在某一直线上运动?若是,请写出该直线对应的函数表达式并说明理由;若不是,请说明理由.
【解答】解:(1)当x=0时,y=﹣2k;当y=0时,x=2,
∴点B坐标为(0,﹣2k),点A坐标(2,0),
∴OA=2,OB=﹣2k,
∵OA=OB,
∴k=﹣2,
∴直线l的函数表达式为y=﹣2x+2;
(2)在Rt△OAD中,AD=,OA=2,
∴OD==1,
∵∠OEB=∠ADO=∠AOB=90°,
∴∠BOE+∠OBE=90°,∠BOE+∠AOD=90°,
∴∠OBE=∠AOD,
∵OB=OA,
在Rt△OBE和Rt△AOD中,
,
∴△OBE≌△AOD(AAS),
∴BE=OD=1;
(3)点P始终在直线y=x上运动,
理由:如图3,过P作PE⊥x轴于E,PF⊥y轴于F,
则∠PFO=∠PEO=∠AOB=90°,
∴∠EPF=90°,
∵△ABP是等腰直角三角形,
∴∠APB=90°,PA=PB,
∴∠BPF=∠APE,
在△PBF与△PAE中,
,
∴△PBF≌△PAE(AAS),
∴PF=PE,
∴点P到x轴的距离等于点P到y轴的距离,
∴动点P在直线y=x上运动.
4.(2021秋 太原期中)综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
(3)请从A,B两题中任选一题作答.我选择 A或B 题.
A.试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由;
B.如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
【解答】解:(1)当y=0时,x+3=0,解得x=﹣6,则A点坐标为(﹣6,0);
当x=0时,y=x+3=3,则B点坐标为(0,3);
(2)将B点坐标(0,3)代入一次函数y=﹣x+b得:b=3,
∴直线BC的表达式为y=﹣x+3,
当y=0时,﹣x+3=0,解得x=3,则C点坐标为(3,0);
(3)A.过点P作PH⊥x轴于H,
设点P(x,x+3),
∴PH=|x+3|,
∵A点坐标为(﹣6,0),C点坐标(3,0),
∴AC=9,
∵S△ACP=AC PH=×9 PH=18,
∴PH=4,
∴x+3=±4,
当x+3=4时,x=2;当x+3=﹣4时,x=﹣14,
∴存在,点P的坐标为(2,4)或(﹣14,﹣4);
B.如图,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.
设点P(x,x+3),则Q(x,﹣x+3),
∴PQ=|x+3﹣(﹣x+3)|=|x|,
∵B点坐标(0,3),C点坐标(3,0),
∴OB=OC=3,
∴BC=3,
∵PQ=BC,
∴|x|=3,解得:x=2或﹣2,
∴存在,点P的坐标为(2,+3)或(﹣2,﹣+3).
5.(2021秋 和平区校级期中)如图,平面直角坐标系中,一次函数y=﹣x+b的图象与x轴交于点A,与y轴交于点B,与正比例函数y=kx的图象交于点C(2,4),在x轴上有一点E(m,0),过点E作直线l⊥x轴,交直线y=kx于点F,交直线y=﹣x+b于点G.
(1)求这两个函数的表达式.
(2)当m=时,点G的坐标为 (,6﹣) ,F的坐标为 (,2) ,△CFG的面积为 .
(3)当GF的长为3时,m的值为 3或1 .
(4)在y轴上找一点P,使以O、C、P为顶点的三角形是等腰三角形,直接写出点P的坐标 (0,8)或(0,2)或p(0,﹣2)或(0,) .
【解答】解:(1)∵正比例函数y=kx的图象过点C(2,4),
∴2k=4,
解得k=2,
∴正比例函数的表达式为y=2x;
∵一次函数y=﹣x+b的图象与正比例函数y=kx的图象交于点C(2,4),
∴4=﹣2+b,
∴b=6,
∴一次函数的表达式为:y=﹣x+6;
(2)∵点G在一次函数y=﹣x+6上,点F在正比例函数y=2x上,且点F.G.E在直线l上,E (m,0),m=,
∴点F、点G横坐标都为,
分别代入一次函数y=﹣x+6,正比例函数y=2x,
∴点G的纵坐标为y=﹣+6=6﹣,点F的纵坐标为y=2,
∴点G的坐标为(,6﹣),F的坐标为(,2),
∴FG=2﹣(6﹣)=3﹣6,
∴S△CFG=×(3﹣6)×(﹣2)=.
故答案为:(,6﹣),(,2),;
(3)①当点F在G点上方,即m>2时,
由(2)知点G的纵坐标为y=﹣m+6,点F的纵坐标为y=2m,
∴GF=2m﹣(﹣m+6)=3m﹣6,
当GF=3时,3m﹣6=3,
解得:m=3;
②当F点在G点下方,即m<2时,
点G的纵坐标为y=﹣m+6,点F的纵坐标为y=2m,
∴GF=(﹣m+6)﹣2m=﹣3m+6,
当GF=3时,﹣3m+6=3,
解得:m=1,
综上,m的值为3或1,
故答案为:3或1;
(4)①当CP=CO时,过点C作CM⊥y轴于M,△PCO为等腰三形,
∴PM=OM,
∵C(2,4),
∴OM=4.
∴PM=4,
∴P(0,8);
②当OP=OC时,
:C(2,4),
∴OC==2,
∴OP=2,
∴P(0,2)或p(0,﹣2);
③当PO=PC时,设P(0,y),
∴PO=|y|,PC==,
解得:y=,
∴P(0,).
故答案为:(0,8)或(0,2)或p(0,﹣2)或(0,).
6.(2021秋 越秀区校级期中)直线AB交x轴于点A(6,0),交y轴于点B(0,6).
(1)如图1,点M为AB的中点,点C在线段OA上,OM交BC于点F.
①求∠BOM的度数;
②如图2,若在线段AB上有点D,且满足BC⊥OD于点E,求证:△BOF≌△OAD.
(2)如图3,当点C在线段OA的延长线上任一点时,以BC为边作等腰Rt△BCG,其中CB=CG,直线GA交y轴于点H,当C在x轴上A点右侧运动时,线段OH的长度是否发生变化?如果不变,求其值;如果变化,求线段OH的取值范围.
【解答】解:(1)①∵点A(6,0),点B(0,6),
∴OA=OB=6,
又∵∠AOB=90°,点M为AB的中点,
∴∠BOM=45°;
②∵BC⊥OD,
∴∠BEO=90°=∠AOB,
∴∠BOE+∠OBE=90°=∠BOE+∠DOA,
∴∠OBE=∠DOA,
∵OA=OB=6,AOB=90°,
∴∠OAB=45°=∠BOM,
在△OAD和△BOF中,
,
∴△OAD≌△BOF(ASA);
(2)线段OH的长度不会变化,OH=6,理由如下:
过G作GN⊥x轴,垂足为N.
∵∠BCG=90°,
∴∠BCO+∠GCN=90°.
∵∠AOB=∠GNC=90°,
∴∠BCO=∠CGN,∠CBO=∠GCN.
∵BC=CG,
∴△BCO≌△CGN(ASA),
∴GN=OC,CN=AO=BO,
∴OC=OA+AC=CN+AC=AN,
∴GN=AN,
∴∠GAN=45°=∠OAH.
∵∠AOH=90°,
∴△OAH是等腰直角三角形,
∴OA=OH=6.
∴无论P点怎么动,OH的长不变.
7.(2021秋 碑林区校级期中)【问题发现】
(1)如图①,将Rt△AOB置于平面直角坐标系中,直角顶点O与原点重合,点A落在x轴上,点B落在y轴上,已知A(4,0),B(0,3),C是x轴上一点,将Rt△AOB沿BC折叠,使点O落在AB边上的点D处,则点C的坐标为 (,0) .
【问题探究】
(2)如图②,将长方形OABC置于平面直角坐标系中,点A在y轴上,点C在x轴上,已知B(12,5),E是OA上一点,将长方形OABC沿CE折叠,点O恰好落在对角线AC上的点F处,求OF所在直线的函数表达式.
(3)如图③,将长方形OABC置于平面直角坐标系中,点A在y轴上,点C在x轴上,已知B(8,6),D在对角线AC上,且CD=OC,P是OD的中点,Q是OC上一点,将△OPQ沿PQ折叠,使点O落在AC边上的点E处,求点D的坐标及四边形OPEQ的面积.
【解答】解:(1)设OC为x,
∵A(4,0),B(0,3),
∴AB===5,
由翻折可知,DB=OB=3,OC=CD=x,
∴AD=2,
由勾股定理得,AD2+CD2=AC2,
即x2+22=(4﹣x)2,
解得x=,
∴点C的坐标为(,0),
故答案为:(,0);
(2)∵长方形OABC,点A在y轴上,点C在x轴上,B(12,5),
∴A(0,5),C(12,0),
设直线AC的解析式为y=kx+b,把A点和C点坐标代入得,
,
解得,
∴直线AC的解析式为y=﹣x+5,
由翻折可知,OC=CF=12,AF=1,
设OE=EF=y,
由勾股定理得,EF2+AF2=AE2,
即y2+12=(5﹣y)2,
解得y=2.4,
即OE=EF=2.4,
∴AE=2.6,
设点F的坐标为(m,﹣m+5),
∴×AF EF=AE yF,
即×1×2.4=×2.6m,
解得m=,
则点F的坐标为(,),
设直线OF的解析式为y=dx,代入F点坐标得,=d,
解得d=5,
∴直线OF的解析式为y=5x;
(3)连接OE,
∵P是OD的中点,
∴OP=PD,
由折叠可知,OP=PD=PE,OE⊥PQ,
∴∠POE=∠PEO,∠PED=∠PDE,
∴∠PEO+∠PED=90°,
∴OE⊥CD,
∴PQ∥CD,
∴Q是OC的中点,
∴三角形OPQ的面积是三角形OCD面积的四分之一,四边形OPEQ的面积是三角形OCD面积的二分之一,
∵B(8,6),
∴A(0,6),C(8,0),
∴AC===10,
∴OA OC=AC OE,
即×6×8=×10×OE,
解得OE=4.8,
∵OC=CD=8,
∴三角形OCD的面积为:CD OE=×8×4.8=19.2,
∴四边形OPEQ的面积是×19.2=9.6,
∵三角形OCD的面积为19.2,OC=8,
∴点D的纵坐标为19.2×2÷8=4.8,
设直线AC的解析式为y=nx+e,把A点和C点坐标代入得,,
解得,
∴直线AC的解析式为y=﹣x+6,
∵点D在直线AC上,当y=4.8时,4.8=﹣x+6,
解得x=1.6,
∴点D的坐标为(1.6,4.8).
8.(2021秋 和平区期中)如图1,直线y=x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)直线BC的函数表达式为 y=﹣x+3 ;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,请直接写出点P的坐标 (﹣,) ;
②若△PQB的面积为,请直接写出点M的坐标 (,0)或(﹣,0) ;
③若点K为线段OB的中点,连接CK,如图2,若在线段OC上有一点F,满足∠CKF=45°,请直接写出点F的坐标 (,0) .
【解答】解:(1)对于y=x+3,令x=0,y=3,
∴B(0,3),
令y=0,
∴x+3=0,
∴x=﹣6,
∴A(﹣6,0),
∵点C与点A关于y轴对称,
∴C(6,0),
设直线BC的解析式为y=kx+b,
∴,
∴,
∴直线BC的解析式为y=﹣x+3,
故答案为:y=﹣x+3;
(2)①设点M(m,0),
∴P(m,m+3),
∵B(0,3),C(6,0),
∴BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,
∵∠MBC=90°,
∴△BMC是直角三角形,
∴BM2+BC2=MC2,
∴m2+9+45=(6﹣m)2,
∴m=﹣,
∴P(﹣,),
故答案为:(﹣,);
②设点M(n,0),
∵点P在直线AB:y=x+3上,
∴P(n,n+3),
∵点Q在直线BC:y=﹣x+3上,
∴Q(n,﹣n+3),
∴PQ=|n+3﹣(﹣n+3)|=|n|,
∵△PQB的面积为,
∴S△PQB=|n| |n|=n2=,
∴n=±,
∴M(,0)或(﹣,0),
故答案为:(,0)或(﹣,0);
③过点F作FH⊥FK交CK于H,过点H作HE⊥x轴于E,
∵∠CKF=45°,
∴△KFH是等腰直角三角形,
∴KF=FH,∠KFO+∠HFE=90°,
∵∠KFO+∠FKO=90°,
∴∠HFE=∠FKO,
∵∠KOF=∠FEH=90°,
∴△KOF≌△FEH(AAS),
∴EH=OF,EF=OK,
∵点K为线段OB的中点,OB=6,
∴EF=OK=,K(0,),
设F(x,0),则OE=x+,EH=OF=x,则H(x+,x),
∵C(6,0),K(0,),
设直线CK的解析式为y=kx+b,
∴,解得:,
∴直线CK的解析式为y=﹣x+,
∵点H在CK上,H(x+,x),
∴x=﹣(x+)+,解得:x=,
∴点F的坐标为(,0).
故答案为:(,0).
9.(2021秋 碑林区校级期中)如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 (1,7) .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MN∥x轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
【解答】解:(1)解方程组,得,
所以点C的坐标为(1,7),
故答案为:(1,7);
(2)∵M是直线AB上一点,
设点M的坐标为(a,a+6),
∵MN∥x轴,点N是直线y=﹣2x+9上一点,
∴a+6=﹣2x+9,解得x=,
∴点N的坐标是(,a+6),
∵MN=6,
∴|﹣a|=6,解得:a=5或﹣3,
∴点M的坐标为(5,11)或(﹣3,3);
(3)存在,
①点M的坐标为(﹣3,3)时,点N的坐标为(3,3),
∴MN=6,MC==,NC==,
设点P的坐标为(x,y),
∵直线y=x+6交x轴于点A,交y轴于点B,
∴B(0,6),OB=6=MN,
当BP=NC,OP=MC时;
,解得:或,
∴点P的坐标为(4,4)或(﹣4,4),
当BP=MC,OP=NC时,
,解得:或,
∴点P的坐标为(4,2)或(﹣4,2),
②点M的坐标为(5,11)时,点N的坐标为(﹣1,11),
∴MN=6,MC==,NC==,
此时△MNC与①中的△MNC三边都对应相等,所以此时情况与①相同.
综上,点P的坐标为(4,4)或(﹣4,4)或(4,2)或(﹣4,2).
10.(2021秋 深圳期中)如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)填空:k= ;b= 4 ;m= 2 ;
(2)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由.
(3)若动点P在射线DC上从点D开始以每秒1个单位的速度运动,连接AP,设点P的运动时间为t秒.是否存在t的值,使△ACP和△ADP的面积比为1:3?若存在,直接写出t的值;若不存在,请说明理由.
【解答】解:(1)∵直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),
∴5=1+b,
∴b=4,
∴直线l2:y=﹣x+4,
∵直线l2:y=﹣x+4经过点C(2,m),
∴m=﹣2+4=2,
∴C(2,2),
把C(2,2)代入y=kx+1,得到k=.
∴k=,b=4,m=2.
故答案为:,4,2;
(2)作点C关于x轴的对称点C′,连接BC′交x轴于E,连接EC,则△BCE的周长最小.
∵B(﹣1,5),C′(2,﹣2),
∴直线BC′的解析式为y=﹣x+,
令y=0,得到x=,
∴E(,0),
∴存在一点E,使△BCE的周长最短,E(,0);
(3)∵点P在射线DC上从点D开始以每秒1个单位的速度运动,直线l1:y=x+1,
∴D(﹣2,0),
∵C(2,2),
∴CD==2,
∵点P的运动时间为t秒.
∴DP=t,
分两种情况:①点P在线段DC上,
∵△ACP和△ADP的面积比为1:3,
∴,
∴,
∴DP=×2=,
∴t=;
②点P在线段DC的延长线上,
∵△ACP和△ADP的面积比为1:3,
∴,
∴=,
∴DP=×2=3,
∴t=3.
综上:存在t的值,使△ACP和△ADP的面积比为1:3,t的值为或3.
11.(2021秋 开福区校级月考)已知直线AB交x轴于点A(a,o),交y轴于点B(0,b),且a、b满足|a+b|+(b﹣4)2=0.
(1)求∠ABO的度数;
(2)如图1,若点C在第一象限,且BE⊥AC于点E,延长BE至点D,使得BD=AC,连接OC、OD、CD,试判断△COD的形状,并说明理由;
(3)如图2,若点C在OB上,点F在AB的延长线上,且AC=CF,△ACP是以AC为直角边的等腰直角三角形,CQ⊥AF于点Q,求的值.
【解答】解:(1)∵|a+b|+(b﹣4)2=0,
∴a=﹣4,b=4,
∴点A的坐标为(﹣4,0),点B的坐标为(0,4),
∴AO=BO=4,
∵∠AOB=90°,
∴∠ABO的度数为45°;
(2)△COD是等腰直角三角形.
证明:如图1:
∵BE⊥AC,OA⊥OB,
∴∠EFB+∠EBF=∠OFA+∠OAF,
又∵∠OFA=∠EFB,
∴∠EBF=∠OAF,
在△AOC与△BOD中,
,
∴△AOC≌△BOD(SAS),
∴OC=OD,∠AOC=∠BOD,
∴∠AOB+∠BOC=∠BOC+∠DOC,
∴∠DOC=∠AOB=90°,
∴△COD为等腰直角三角形;
(3)过点C作CK⊥OB交AB于K,
∵∠ACP=90°,
∴∠BCP=∠OAC,
∵OA=OB,
∴∠OAC+∠CAF=∠OAB=45°,
∴∠OBA=∠F+∠BCF=45°,
∵AC=CF,
∴∠CAF=∠F,
∴∠BCF=∠OAC=∠BCP,即OB平分∠PCF,
∵△ACP是以AC为直角边的等腰直角三角形,
∴CA=CP,
∵AC=CF,
∴CP=CF,
∵CB=CB,
∴△BCF≌△BCP (SAS),
∴BF=BP,
∵∠OBA=45°,CK⊥OB,
∴△BCK为等腰直角三角形,
∴△ACF和△BCK均为等腰三角形,
∵CQ⊥AF,
∴FQ=AQ,BQ=QK,
∴BF=AK,
∵△BCK为等腰直角三角形,
∴BQ=QK=CQ,
∴===2.
12.(2021 南岗区校级开学)如图,直线y=x+6交x轴于A,交y轴于B,把△AOB绕着点O顺时针旋转,得到△COD,且点D在x轴正半轴上,延长AB交CD于点E.
(1)求直线CD的解析式;
(2)点P为线段DE上一点,连接PA、PB,设点P的横坐标为m,△PAB的面积为S,求S与m的函数解析式;
(3)在(2)的条件下,点Q为OD边上一点,若∠PQC=2∠OCQ,PQ+CQ=PA,求点P的坐标.
【解答】解:∵直线y=x+6交x轴于A,交y轴于B,
∴A(﹣12,0),B(0,6),
∴OA=12,OB=6,
∵把△AOB绕着点O顺时针旋转,得到△COD,
∴OC=OA=12,OD=OB=6,
∴C(0,12),D(6,0),
设直线CD的解析式为y=kx+b,
则,
解得:,
∴直线CD的解析式为y=﹣2x+12;
(2)如图1,∵点P在直线CD上且横坐标为m,
∴P(m,﹣2m+12),
设直线PA的解析式为y=ax+c,将P(m,﹣2m+12),A(﹣12,0)代入,
得:,
解得:,
∴直线PA的解析式为y=x+,
∵直线PA交y轴于点F,
∴F(0,),
∴OF=,
∴BF=OB﹣OF=6﹣=,
∴S△PAB=S△FAB+S△PBF=BF OA+BF xP=××(12+m)=15m﹣36,
∴S=15m﹣36;
(3)如图2,延长PQ交y轴于F,过点P作PH⊥x轴于点H,作PG⊥OC于点G,连接AF,
∵∠PQC=2∠OCQ,
∴180°﹣∠CQO﹣∠PQD=2(90°﹣∠CQO),
∴∠CQO=∠PQD,
∵∠FQO=∠PQD,
∴∠CQO=∠FQO,
∵∠COQ=∠FOQ=90°,OQ=OQ,
∴△COQ≌△FOQ(ASA),
∴OF=OC=12,QC=QF,
∵PQ+CQ=PA,
∴PQ+QF=PA,
即PF=PA,
∴∠PAF=∠PFA,
∵OA=OF=12,
∴∠OAF=∠OFA,
∴∠PAF﹣∠OAF=∠PFA﹣∠OFA,
即∠PAH=∠PFG,
∵∠PHA=∠PGF=90°,PA=PF,
∴△PHA≌△PGF(AAS),
∴PH=PG,
∴﹣2m+12=m,
解得:m=4,
∴P(4,4).
13.(2021春 黄陂区期末)如图,直线l1:y=kx﹣2k+1经过定点C,分别交x轴,y轴于A,B两点,直线l2经过O,C两点,点Dl2上.
(1)①直接写出点C的坐标为 (2,1) ;②求直线l2的解析式;
(2)如图1,若S△BOC=2S△BCD,求点D的坐标;
(3)如图2,直线l3经过D,E(0,﹣)两点,分别交x轴的正半轴、l1于点P,F,若PE=PF,∠EDO=45°,求k的值.
【解答】解(1)①∵y=kx﹣2k+1经过定点C,
∴点C的坐标与k的取值无关,
∴x=2时,y=1,
∴C(2,1),
故答案为:(2,1);
②设l2的解析式为:y=ax,
把C(2,1)代入y=ax得:a=,
∴l2的解析式为y=,
(2)如图,取OB的中点H,连接CH,
∵C(2,1),
∵S△BOC=2S△BCD,
当点D在线段OC上时,
则点D为OC的中点,
∴D(1,);
当点D在线段DC的延长线时,
∴S△BCD=,
即OB=,|xD|=3,
∴D(3,),
综上所述,符合条件的点D坐标为(1,)或(3,).
(3)过点C作CH∥EF,过点O作OH⊥OC,分别过点C,H作CM⊥OB于M,MN⊥OB于N,
∵∠EDO=45°,
∴∠OCH=45°,
∴OC=OH,
又∵∠MOC=∠NHO,∠OMC=∠ONH,
∴△COM≌△OHN(AAS),
∴CM=OH,OM=NH,
由C(2,1)得:H(1,﹣2),
∴yCH=3x﹣5,
由E(0,﹣)得:yEF=3x﹣,
∴P(,0),
过点F作FK⊥OA于K,
∵PF=PE,
∴△OPE≌△FPK(AAS),
∴F(1,),
将F(1,)代入l1:y=kx﹣2k+1,
∴k﹣2k+1=,
解得k=﹣.
14.(2021春 东港区校级期末)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0),(12,6),直线y=﹣x+b(b>0)与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣x+b(b>0)平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,过点P的直线,与直线BC和x轴分别交于点N、M.问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长,若不存在,请说明理由.
(3)将(1)中的直线沿y轴向下平移a个单位得到新直线l,矩形OABC沿平移后的直线折叠,若点O落在边BC上的F处,CF=9,求出a的值.
【解答】解:(1)∵直线y=﹣x+b(b>0)平分矩形OABC的面积,
∴直线过矩形的中心,
∵B(12,6),
∴矩形中心为(6,3),
∴﹣6+b=3,
解得b=12;
(2)如图,假设存在ON平分∠CNM的情况,
当PM与线段BC,OA交于N,M时,
过点O作OH⊥MN于H,
∵ON平分∠CNM,OC⊥BC,OH⊥MN,
∴OH=OC=6,
∵OP=12,
∴∠OPN=30°,
∴OM=OP=4,
当y=0时,﹣,解得x=8,
∴OD=8,
∴DM=OD﹣OM=8﹣4;
当PM与直线BC,OA交于N,M时,如图,
同理可得,此时DM=OD+OM=8+4,
综上:存在ON平分∠CNM的情况,此时DM=8﹣4或8+4;
(3)设平移后的直线y=﹣与y轴交于点P',沿此直线折叠,点O的对应点恰好落在BC边上F处,连接P'F,OF,
则有OP'=P'F=m,CP'=m﹣6,
在Rt△CP'F中,由勾股定理得:
(m﹣6)2+92=m2,
解得m=,
∴PP'=12﹣=,
∴a=.
15.(2021春 连山区期末)如图,矩形OABC在平面直角坐标系中,OA在x轴负半轴,OC在y轴正半轴,点D在边OC上,连接BD,将△BCD沿BD折叠,得到△BDE,使点E落在矩形OABC内部,过点E作EF⊥AB于F,直线CF交x轴于点M,若点E(﹣3,9),F恰为AB中点.
(1)如图1,直线CM的解析式;
(2)如图2,点P为x轴上的动点,过P作x轴的垂线,分别交直线CM、BD于点N、Q,若NQ=2CD,求点P坐标;
(3)点H为直线BD上动点,若△AEH以AE为直角边的直角三角形,是否存在点H?如果存在,直接写出点H坐标;不存在,请说明理由!
【解答】解:(1)延长FE交OC于点H,如图:
设OA=m,由折叠可知BC=BE=OA=m,
∵点E(﹣3,9),
∴AF=9,EH=3,EF=m﹣3,
∵F恰为AB中点,
∴BF=AF=9,OC=AB=18,
∴C(0,18),
在Rt△BEF中,由勾股定理得BE2=BF2+EF2,
∴m2=92+(m﹣3)2,
∴m=15,
∴F(﹣15,9),
设直线CM的解析式为y=kx+b,将C(0,18),F(﹣15,9)代入得:
,
解得,
∴直线CM解析式为:;
(2)如图:
设CD=n,则DE=n,DH=9﹣n,
在Rt△DEH中,DE2=DH2+EH2,
∴n2=(9﹣n)2+32,解得n=5,
∴CD=5,
∴OD=13,
∴D(0,13),
∵B(﹣15,18)
∴直线BD解析式为:
设P(t,0),则N(t,t+18),Q(t,﹣t+13),
∴NQ=|(t+18)﹣(﹣t+13)|=|t+5|,
∵NQ=2CD=10,
∴|t+5|=10,
解得t=或t=﹣,
∴P(,0)或P(﹣,0);
(3)存在,理由如下:
由(2)知直线BD为:,
设H(s,﹣s+13),而A(﹣15,0),E(﹣3,9),
∴AH2=(s+15)2+(﹣s+13)2,EH2=(s+3)2+(﹣s+4)2,AE2=122+(﹣9)2=225,
当EH为斜边时,EH2=AH2+AE2,
∴(s+3)2+(﹣s+4)2=(s+15)2+(﹣s+13)2+225,解得s=﹣33,
∴H(﹣33,24),
当AH为斜边时,AH2=EH2+AE2,
∴(s+15)2+(﹣s+13)2=(s+3)2+(﹣s+4)2+225,
解得s=﹣8,
∴H(﹣8,),
综上所述,H坐标为(﹣33,24)或(﹣8,).
16.(2021春 铁锋区期末)综合与探究.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0)、点B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)直接写出AB的长 5 ;
(2)点C的坐标 (8,0) ,点D的坐标 D(0,﹣6) ;
(3)求直线AB的函数表达式;
(4)y轴上是否存在一点P,使得S△PAB=S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵A(3,0)、B(0,4),
∴OA=3,OB=4,
∵∠AOB=90°,
∴AB=;
故答案为:5;
(2)设直线AB的表达式为y=kx+b,将A(3,0)、B(0,4)代入,
得:,
解得:,
∴直线AB的表达式为y=﹣x+4;
(3)由折叠得:AC=AB=5,
∴OC=OA+AC=3+5=8,
∴点C的坐标为(8,0),
设点D(0,m),则OD=﹣m,
由折叠得CD=BD=4﹣m,
在Rt△OCD中,OC2+OD2=CD2,
∴82+(﹣m)2=(4﹣m)2,
解得:m=﹣6,
∴D(0,﹣6),
故答案为:C(8,0),D(0,﹣6);
(4)存在,设点P(0,n),
∴PB=|n﹣4|,
∵S△PAB=S△OCD,
∴PB OA=××OC×OD,
即|n﹣4|×3=××8×6,
解得:n=12或﹣4,
∴P(0,12)或(0,﹣4).
17.(2021春 集贤县期末)如图1,平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
(1)求点C的坐标及直线AB的表达式;
(2)如图2,在x轴上有一点E,过点E作直线l⊥x轴,交直线y=2x于点F,交直线y=kx+b于点G,若GF的长为3,求点E的坐标;
(3)在y轴上是否存在一点M,使以O、C、M为顶点的三角形是等腰三角形,若存在,直接写出点M的坐标;若不存在,说明理由.
【解答】解:(1)∵点C在直线y=2x上,
∴2a=4,
解得a=2,
∴C(2,4);
将A(6,0),C(2,4)代入直线y=kx+b,得:
,
解得,
∴直线AB的解析式为:y=﹣x+6;
(2)根据题意设E点坐标为(m,0),
∵点E、F、G三点在同一直线上,且点F在直线y=2x上,点G在y=﹣x+6上,
∴F(m,2m),G(m,﹣m+6),
又∵|FG|=3,
∴|2m﹣(﹣m+6)|=3,
解得m=3或m=1,
∴E点的坐标为(3,0)或(1,0);
(3)存在,
设M(0,t),
∵C(2,4),
∴OC==2,OM=|t|,CM==,
要使以O、C、M为顶点的三角形是等腰三角形,分以下三种情况:
①当OC=OM时,
即|t|=2,
解得t=±2,
∴M(0,2)或(0,﹣2);
②当OC=CM时,
即=2,
解得t=8或t=0(舍去),
∴M(0,8);
③当CM=OM时,
即=|t|,
解得t=,
∴M(0,);
综上,符合条件的M点的坐标是(0,2)或(0,﹣2)或(0,8)或(0,).
18.(2021春 天心区期末)我们知道一次函数y=mx+n与y=﹣mx+n(m≠0)的图象关于y轴对称,所以我们定义:函数y=mx+n与y=﹣mx+n(m≠0)互为“M”函数.
(1)请直接写出函数y=2x+5的“M”函数;
(2)如果一对“M”函数y=mx+n与y=﹣mx+n(m≠0)的图象交于点A,且与x轴交于B,C两点,如图所示,若∠BAC=90°,且△ABC的面积是8,求这对“M”函数的解析式;
(3)在(2)的条件下,若点D是y轴上的一个动点,当△ABD为等腰三角形时,请求出点D的坐标.
【解答】(1)解:根据互为“M”函数的定义,
∴函数y=2x+5的“M”函数为y=﹣2x+5;
(2)解:根据题意,y=mx+n 和 y=﹣mx+n 为一对“M函数”.
∴AB=AC,
又∵∠BAC=90°,
∴△ABC 为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∵OB=OC,
∴∠BAO=∠CAO=45°,
∴OA=OB=OC,
又∵ 且 BC=2AO,
∴,
∵A、B、C是一次函数y=mx+n与y=﹣mx+n(m≠0)的图象于坐标轴的交点,
∴A(0,n),B(﹣,0),C(,0),
∵OA=OB=n,
∴=2,
∴m=1,
∴ 和 ;
(3)解:根据等腰三角形的性质,分情况,
∵,
∴AB=4,
由(2)知,A(0,2),B(﹣2,0),C(2,0),
∴①以 A 为顶点,则 AB=AD,
当点D在点A上方时,AD=2+4,
当点D在点A下方时,AD=2﹣4,
∴D1(0,2+4),D2(0,2﹣4),
②以 B 为顶点,则 BA=BD,
此时点D在y轴负半轴,
∴D3(0,﹣2),
③以 D 为顶点,则 DA=DB,
此时D为坐标原点,
∴D4(0,0).
∴D点坐标为 D1(0,2+4),D2(0,2﹣4),D3(0,﹣2),∴D4(0,0).
19.(2021春 洪泽区期末)如图,直线y=﹣x+12与x轴交于点A(12,0),与直线OB交于点B(8,4),x轴上一点P从O点出发以每秒2个单位的速度向终点A运动,作PE⊥x轴交OB于E,过E作EF∥x轴且EF=PE,以PE、EF为边作矩形PEFG,设运动时间为t.
(1)当点F落在直线AB上时,求t的值;
(2)在运动过程中,设矩形PEFG与△ABO的重叠部分面积为S,求S与t的关系式,并写出相应的t的取值范围;
(3)矩形PEFG的对角线交于点Q,直接写出PQ+AQ的最小值为 .
【解答】解:(1)如图1,设直线OB的解析式为y=kx,
∵点B(8,4)在直线y=kx上,
∴8k=4,
解得,k=,
∴y=x,
∵OP=2t,
∴P(2t,0),E(2t,t),
∵EF=PE=t,
∴F(t,t),G(t,0),
当点F落在直线AB上时,则t+12=t,解得t=.
(2)当点E与点B重合时,则2t=8,解得t=4;
当点G与点A重合时,则t=12,解得t=;
当点P与点A重合时,则2t=12,解得t=6,
当0<t≤时,如图1,PE=t,EF=t,
∴S=t t=t2;
当<t≤4时,如图2,设直线y=﹣x+12交y轴于点C,则C(0,12),
∴OA=OC=12,
∵∠AOC=90°,
∴∠OAC=∠OCA=45°,
设EF、FG分别交AB于点J、点K,则∠FKJ=∠OCA=45°,∠FJK=∠OAC=45°,
∴JF=FK;
对于y=﹣x+12,当x=t时,y=t+12,
∴K(t,t+12),
∴FK=t﹣(t+12)=t﹣12,
∴S=t2﹣(t﹣12)2=t2+42t﹣72;
当4<t≤时,如图3,∠GKA=∠PJA=∠OAC=45°,
∴PA=PJ=12﹣2t,GA=GK=12t,
∴S=(12﹣2t)2(12t)2=t2+6t;
当<t≤6时,如图4,S=(12﹣2t)2=2t2﹣24t+72,
综上所述,S=.
(3)如图4,连接AE、GE,由矩形的性质可知,点Q在GE上,且PQ=EQ,
∴PQ+AQ=EQ+AQ≥AE,
∴当点Q落在AE上,且AE最小时,PQ+AQ的值最小;
如图5,点G与点A重合,则AE与GE重合,
∴点Q在AE上,
∴PQ+AQ=AE,
此时t=,
∴OP=2t=2×=,
∴AP=12﹣=,
∴PE=2×=,
∴AE==;
作BD⊥x轴于点D,作AE′⊥OB于点E′,则OB==4,
由S△OAB=×OB AE′=OA BD,得×AE′=×12×4,解得AE′=,
∴AE=AE′,
∴AE的长就是点A到直线OB的距离,
∴AE⊥OB,
∴AE的值最小,此时PQ+AQ的值最小,为,
故答案为:.
1.(2021秋 海珠区校级期中)如图所示,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足,C的坐标为(﹣1,0),且AH⊥BC于点H,AH交OB于点P.
(1)如图1,写出a、b的值,证明△AOP≌△BOC;
(2)如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,求证:S△BDM﹣S△ADN=4.
2.(2021秋 高新区校级期中)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求出点A、点B的坐标;
(2)求△COB的面积;
(3)在y轴上是否存在一点P,使得△PBC为等腰三角形?若存在,请直接写出点P坐标,若不存在,请说明理由.
3.(2021秋 苏家屯区期中)如图1所示,直线l:y=k(x﹣2)(k<0)与x轴正半轴和y轴正半轴分别交于点A、B两点.
(1)当OA=OB时,求直线l的表达式;
(2)在(1)的条件下,如图2所示,设C为线段AB延长线上一点,作直线OC,过点A、B两点分别作AD⊥OC于点D,BE⊥OC于点E,若AD=,求BE的长;
(3)如图3所示,当K取不同的值时,点B在y轴正半轴上运动,以AB为底向上作等腰直角△ABP,试问:B点运动时,点P是否始终在某一直线上运动?若是,请写出该直线对应的函数表达式并说明理由;若不是,请说明理由.
4.(2021秋 太原期中)综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
(3)请从A,B两题中任选一题作答.我选择 题.
A.试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由;
B.如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
5.(2021秋 和平区校级期中)如图,平面直角坐标系中,一次函数y=﹣x+b的图象与x轴交于点A,与y轴交于点B,与正比例函数y=kx的图象交于点C(2,4),在x轴上有一点E(m,0),过点E作直线l⊥x轴,交直线y=kx于点F,交直线y=﹣x+b于点G.
(1)求这两个函数的表达式.
(2)当m=时,点G的坐标为 ,F的坐标为 ,△CFG的面积为 .
(3)当GF的长为3时,m的值为 .
(4)在y轴上找一点P,使以O、C、P为顶点的三角形是等腰三角形,直接写出点P的坐标 .
6.(2021秋 越秀区校级期中)直线AB交x轴于点A(6,0),交y轴于点B(0,6).
(1)如图1,点M为AB的中点,点C在线段OA上,OM交BC于点F.
①求∠BOM的度数;
②如图2,若在线段AB上有点D,且满足BC⊥OD于点E,求证:△BOF≌△OAD.
(2)如图3,当点C在线段OA的延长线上任一点时,以BC为边作等腰Rt△BCG,其中CB=CG,直线GA交y轴于点H,当C在x轴上A点右侧运动时,线段OH的长度是否发生变化?如果不变,求其值;如果变化,求线段OH的取值范围.
7.(2021秋 碑林区校级期中)【问题发现】
(1)如图①,将Rt△AOB置于平面直角坐标系中,直角顶点O与原点重合,点A落在x轴上,点B落在y轴上,已知A(4,0),B(0,3),C是x轴上一点,将Rt△AOB沿BC折叠,使点O落在AB边上的点D处,则点C的坐标为 .
【问题探究】
(2)如图②,将长方形OABC置于平面直角坐标系中,点A在y轴上,点C在x轴上,已知B(12,5),E是OA上一点,将长方形OABC沿CE折叠,点O恰好落在对角线AC上的点F处,求OF所在直线的函数表达式.
(3)如图③,将长方形OABC置于平面直角坐标系中,点A在y轴上,点C在x轴上,已知B(8,6),D在对角线AC上,且CD=OC,P是OD的中点,Q是OC上一点,将△OPQ沿PQ折叠,使点O落在AC边上的点E处,求点D的坐标及四边形OPEQ的面积.
8.(2021秋 和平区期中)如图1,直线y=x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)直线BC的函数表达式为 ;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,请直接写出点P的坐标 ;
②若△PQB的面积为,请直接写出点M的坐标 ;
③若点K为线段OB的中点,连接CK,如图2,若在线段OC上有一点F,满足∠CKF=45°,请直接写出点F的坐标 .
9.(2021秋 碑林区校级期中)如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MN∥x轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
10.(2021秋 深圳期中)如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)填空:k= ;b= ;m= ;
(2)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由.
(3)若动点P在射线DC上从点D开始以每秒1个单位的速度运动,连接AP,设点P的运动时间为t秒.是否存在t的值,使△ACP和△ADP的面积比为1:3?若存在,直接写出t的值;若不存在,请说明理由.
11.(2021秋 开福区校级月考)已知直线AB交x轴于点A(a,o),交y轴于点B(0,b),且a、b满足|a+b|+(b﹣4)2=0.
(1)求∠ABO的度数;
(2)如图1,若点C在第一象限,且BE⊥AC于点E,延长BE至点D,使得BD=AC,连接OC、OD、CD,试判断△COD的形状,并说明理由;
(3)如图2,若点C在OB上,点F在AB的延长线上,且AC=CF,△ACP是以AC为直角边的等腰直角三角形,CQ⊥AF于点Q,求的值.
12.(2021 南岗区校级开学)如图,直线y=x+6交x轴于A,交y轴于B,把△AOB绕着点O顺时针旋转,得到△COD,且点D在x轴正半轴上,延长AB交CD于点E.
(1)求直线CD的解析式;
(2)点P为线段DE上一点,连接PA、PB,设点P的横坐标为m,△PAB的面积为S,求S与m的函数解析式;
(3)在(2)的条件下,点Q为OD边上一点,若∠PQC=2∠OCQ,PQ+CQ=PA,求点P的坐标.
13.(2021春 黄陂区期末)如图,直线l1:y=kx﹣2k+1经过定点C,分别交x轴,y轴于A,B两点,直线l2经过O,C两点,点Dl2上.
(1)①直接写出点C的坐标为 ;②求直线l2的解析式;
(2)如图1,若S△BOC=2S△BCD,求点D的坐标;
(3)如图2,直线l3经过D,E(0,﹣)两点,分别交x轴的正半轴、l1于点P,F,若PE=PF,∠EDO=45°,求k的值.
14.(2021春 东港区校级期末)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0),(12,6),直线y=﹣x+b(b>0)与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣x+b(b>0)平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,过点P的直线,与直线BC和x轴分别交于点N、M.问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长,若不存在,请说明理由.
(3)将(1)中的直线沿y轴向下平移a个单位得到新直线l,矩形OABC沿平移后的直线折叠,若点O落在边BC上的F处,CF=9,求出a的值.
15.(2021春 连山区期末)如图,矩形OABC在平面直角坐标系中,OA在x轴负半轴,OC在y轴正半轴,点D在边OC上,连接BD,将△BCD沿BD折叠,得到△BDE,使点E落在矩形OABC内部,过点E作EF⊥AB于F,直线CF交x轴于点M,若点E(﹣3,9),F恰为AB中点.
(1)如图1,直线CM的解析式;
(2)如图2,点P为x轴上的动点,过P作x轴的垂线,分别交直线CM、BD于点N、Q,若NQ=2CD,求点P坐标;
(3)点H为直线BD上动点,若△AEH以AE为直角边的直角三角形,是否存在点H?如果存在,直接写出点H坐标;不存在,请说明理由!
16.(2021春 铁锋区期末)综合与探究.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0)、点B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)直接写出AB的长 ;
(2)点C的坐标 ,点D的坐标 ;
(3)求直线AB的函数表达式;
(4)y轴上是否存在一点P,使得S△PAB=S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.
17.(2021春 集贤县期末)如图1,平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
(1)求点C的坐标及直线AB的表达式;
(2)如图2,在x轴上有一点E,过点E作直线l⊥x轴,交直线y=2x于点F,交直线y=kx+b于点G,若GF的长为3,求点E的坐标;
(3)在y轴上是否存在一点M,使以O、C、M为顶点的三角形是等腰三角形,若存在,直接写出点M的坐标;若不存在,说明理由.
18.(2021春 天心区期末)我们知道一次函数y=mx+n与y=﹣mx+n(m≠0)的图象关于y轴对称,所以我们定义:函数y=mx+n与y=﹣mx+n(m≠0)互为“M”函数.
(1)请直接写出函数y=2x+5的“M”函数;
(2)如果一对“M”函数y=mx+n与y=﹣mx+n(m≠0)的图象交于点A,且与x轴交于B,C两点,如图所示,若∠BAC=90°,且△ABC的面积是8,求这对“M”函数的解析式;
(3)在(2)的条件下,若点D是y轴上的一个动点,当△ABD为等腰三角形时,请求出点D的坐标.
19.(2021春 洪泽区期末)如图,直线y=﹣x+12与x轴交于点A(12,0),与直线OB交于点B(8,4),x轴上一点P从O点出发以每秒2个单位的速度向终点A运动,作PE⊥x轴交OB于E,过E作EF∥x轴且EF=PE,以PE、EF为边作矩形PEFG,设运动时间为t.
(1)当点F落在直线AB上时,求t的值;
(2)在运动过程中,设矩形PEFG与△ABO的重叠部分面积为S,求S与t的关系式,并写出相应的t的取值范围;
(3)矩形PEFG的对角线交于点Q,直接写出PQ+AQ的最小值为 .
参考答案与试题解析
1.(2021秋 海珠区校级期中)如图所示,直线AB交x轴于点A(a,0),交y轴于点B(0,b),且a、b满足,C的坐标为(﹣1,0),且AH⊥BC于点H,AH交OB于点P.
(1)如图1,写出a、b的值,证明△AOP≌△BOC;
(2)如图2,连接OH,求证:∠OHP=45°;
(3)如图3,若点D为AB的中点,点M为y轴正半轴上一动点,连接MD,过D作DN⊥DM交x轴于N点,当M点在y轴正半轴上运动的过程中,求证:S△BDM﹣S△ADN=4.
【解答】(1)解:∵+(a﹣4)2=0,
∴a+b=0,a﹣4=0,
∴a=4,b=﹣4,
则OA=OB=4.
∵AH⊥BC即∠AHC=90°,∠COB=90°,
∴∠HAC+∠ACH=∠OBC+∠OCB=90°,
∴∠HAC=∠OBC.
在△OAP与△OBC中,
,
∴△OAP≌△OBC(ASA);
(2)证明:过O分别作OM⊥CB于M点,作ON⊥HA于N点.
在四边形OMHN中,∠MON=360°﹣3×90°=90°,
∴∠COM=∠PON=90°﹣∠MOP.
∵△OAP≌△OBC,
∴OC=OP,
在△COM与△PON中,
,
∴△COM≌△PON(AAS),
∴OM=ON.
∵OM⊥CB,ON⊥HA,
∴HO平分∠CHA,
∴∠OHP=∠CHA=45°;
(3)证明:如图:连接OD.
∵∠AOB=90°,OA=OB,D为AB的中点,
∴OD⊥AB,∠BOD=∠AOD=45°,OD=DA=BD,
∴∠OAD=45°,∠MOD=90°+45°=135°,
∴∠DAN=135°=∠MOD.
∵MD⊥ND即∠MDN=90°,
∴∠MDO=∠NDA=90°﹣∠MDA.
在△ODM与△ADN中,
,
∴△ODM≌△ADN(ASA),
∴S△ODM=S△ADN.
∴S△BDM﹣S△ADN=S△BDM﹣S△ODM=S△BOD=S△AOB=×AO BO=××4×4=4.
2.(2021秋 高新区校级期中)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为y=﹣x+3,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求出点A、点B的坐标;
(2)求△COB的面积;
(3)在y轴上是否存在一点P,使得△PBC为等腰三角形?若存在,请直接写出点P坐标,若不存在,请说明理由.
【解答】解:(1)对于直线l2的解析式为y=﹣x+3,令x=0,得到y=3,
∴B(0,3),
令y=0,得到x=6,
∴A(6,0).
∴点A是坐标为(6,0),点B的坐标为(0,3);
(2)联立y=x,y=﹣x+3并解得:x=2,
∴点C(2,2),
∴S△COB=OB xC=×3×2=3;
(3)存在.
∵点B(0,3),点C(2,2),
∴BC==,
设P(0,y),
①当PC=BC=时,如图,
又∵点C(2,2),
∴PC2=22+(2﹣y)2,
∴()2=22+(2﹣y)2,
∴y=1或3,
∵y=3时,与点B重合,故舍去,
∴点P(0,1);
②当BP=BC=时,如图,
OP=OB+PB=3+,OP′=OB﹣P′B=3﹣,
∴点P(0,3+),(0,3﹣);
③当PB=PC时,如图,
∵PB2=PC2,
∴(3﹣y)2=22+(2﹣y)2,
∴解得:y=,
∴点P(0,),
综上所述:点P坐标为(0,3+),(0,3﹣),(0,1),(0,).
3.(2021秋 苏家屯区期中)如图1所示,直线l:y=k(x﹣2)(k<0)与x轴正半轴和y轴正半轴分别交于点A、B两点.
(1)当OA=OB时,求直线l的表达式;
(2)在(1)的条件下,如图2所示,设C为线段AB延长线上一点,作直线OC,过点A、B两点分别作AD⊥OC于点D,BE⊥OC于点E,若AD=,求BE的长;
(3)如图3所示,当K取不同的值时,点B在y轴正半轴上运动,以AB为底向上作等腰直角△ABP,试问:B点运动时,点P是否始终在某一直线上运动?若是,请写出该直线对应的函数表达式并说明理由;若不是,请说明理由.
【解答】解:(1)当x=0时,y=﹣2k;当y=0时,x=2,
∴点B坐标为(0,﹣2k),点A坐标(2,0),
∴OA=2,OB=﹣2k,
∵OA=OB,
∴k=﹣2,
∴直线l的函数表达式为y=﹣2x+2;
(2)在Rt△OAD中,AD=,OA=2,
∴OD==1,
∵∠OEB=∠ADO=∠AOB=90°,
∴∠BOE+∠OBE=90°,∠BOE+∠AOD=90°,
∴∠OBE=∠AOD,
∵OB=OA,
在Rt△OBE和Rt△AOD中,
,
∴△OBE≌△AOD(AAS),
∴BE=OD=1;
(3)点P始终在直线y=x上运动,
理由:如图3,过P作PE⊥x轴于E,PF⊥y轴于F,
则∠PFO=∠PEO=∠AOB=90°,
∴∠EPF=90°,
∵△ABP是等腰直角三角形,
∴∠APB=90°,PA=PB,
∴∠BPF=∠APE,
在△PBF与△PAE中,
,
∴△PBF≌△PAE(AAS),
∴PF=PE,
∴点P到x轴的距离等于点P到y轴的距离,
∴动点P在直线y=x上运动.
4.(2021秋 太原期中)综合与探究:
如图1,平面直角坐标系中,一次函数y=x+3图象分别交x轴、y轴于点A,B,一次函数y=﹣x+b的图象经过点B,并与x轴交于点C点P是直线AB上的一个动点.
(1)求A,B两点的坐标;
(2)求直线BC的表达式,并直接写出点C的坐标;
(3)请从A,B两题中任选一题作答.我选择 A或B 题.
A.试探究直线AB上是否存在点P,使以A,C,P为顶点的三角形的面积为18?若存在,求出点P的坐标;若不存在,说明理由;
B.如图2,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.试探究直线AB上是否存在点P,使PQ=BC?若存在,求出点P的坐标;若不存在,说明理由.
【解答】解:(1)当y=0时,x+3=0,解得x=﹣6,则A点坐标为(﹣6,0);
当x=0时,y=x+3=3,则B点坐标为(0,3);
(2)将B点坐标(0,3)代入一次函数y=﹣x+b得:b=3,
∴直线BC的表达式为y=﹣x+3,
当y=0时,﹣x+3=0,解得x=3,则C点坐标为(3,0);
(3)A.过点P作PH⊥x轴于H,
设点P(x,x+3),
∴PH=|x+3|,
∵A点坐标为(﹣6,0),C点坐标(3,0),
∴AC=9,
∵S△ACP=AC PH=×9 PH=18,
∴PH=4,
∴x+3=±4,
当x+3=4时,x=2;当x+3=﹣4时,x=﹣14,
∴存在,点P的坐标为(2,4)或(﹣14,﹣4);
B.如图,过点P作x轴的垂线,交直线BC于点Q,垂足为点H.
设点P(x,x+3),则Q(x,﹣x+3),
∴PQ=|x+3﹣(﹣x+3)|=|x|,
∵B点坐标(0,3),C点坐标(3,0),
∴OB=OC=3,
∴BC=3,
∵PQ=BC,
∴|x|=3,解得:x=2或﹣2,
∴存在,点P的坐标为(2,+3)或(﹣2,﹣+3).
5.(2021秋 和平区校级期中)如图,平面直角坐标系中,一次函数y=﹣x+b的图象与x轴交于点A,与y轴交于点B,与正比例函数y=kx的图象交于点C(2,4),在x轴上有一点E(m,0),过点E作直线l⊥x轴,交直线y=kx于点F,交直线y=﹣x+b于点G.
(1)求这两个函数的表达式.
(2)当m=时,点G的坐标为 (,6﹣) ,F的坐标为 (,2) ,△CFG的面积为 .
(3)当GF的长为3时,m的值为 3或1 .
(4)在y轴上找一点P,使以O、C、P为顶点的三角形是等腰三角形,直接写出点P的坐标 (0,8)或(0,2)或p(0,﹣2)或(0,) .
【解答】解:(1)∵正比例函数y=kx的图象过点C(2,4),
∴2k=4,
解得k=2,
∴正比例函数的表达式为y=2x;
∵一次函数y=﹣x+b的图象与正比例函数y=kx的图象交于点C(2,4),
∴4=﹣2+b,
∴b=6,
∴一次函数的表达式为:y=﹣x+6;
(2)∵点G在一次函数y=﹣x+6上,点F在正比例函数y=2x上,且点F.G.E在直线l上,E (m,0),m=,
∴点F、点G横坐标都为,
分别代入一次函数y=﹣x+6,正比例函数y=2x,
∴点G的纵坐标为y=﹣+6=6﹣,点F的纵坐标为y=2,
∴点G的坐标为(,6﹣),F的坐标为(,2),
∴FG=2﹣(6﹣)=3﹣6,
∴S△CFG=×(3﹣6)×(﹣2)=.
故答案为:(,6﹣),(,2),;
(3)①当点F在G点上方,即m>2时,
由(2)知点G的纵坐标为y=﹣m+6,点F的纵坐标为y=2m,
∴GF=2m﹣(﹣m+6)=3m﹣6,
当GF=3时,3m﹣6=3,
解得:m=3;
②当F点在G点下方,即m<2时,
点G的纵坐标为y=﹣m+6,点F的纵坐标为y=2m,
∴GF=(﹣m+6)﹣2m=﹣3m+6,
当GF=3时,﹣3m+6=3,
解得:m=1,
综上,m的值为3或1,
故答案为:3或1;
(4)①当CP=CO时,过点C作CM⊥y轴于M,△PCO为等腰三形,
∴PM=OM,
∵C(2,4),
∴OM=4.
∴PM=4,
∴P(0,8);
②当OP=OC时,
:C(2,4),
∴OC==2,
∴OP=2,
∴P(0,2)或p(0,﹣2);
③当PO=PC时,设P(0,y),
∴PO=|y|,PC==,
解得:y=,
∴P(0,).
故答案为:(0,8)或(0,2)或p(0,﹣2)或(0,).
6.(2021秋 越秀区校级期中)直线AB交x轴于点A(6,0),交y轴于点B(0,6).
(1)如图1,点M为AB的中点,点C在线段OA上,OM交BC于点F.
①求∠BOM的度数;
②如图2,若在线段AB上有点D,且满足BC⊥OD于点E,求证:△BOF≌△OAD.
(2)如图3,当点C在线段OA的延长线上任一点时,以BC为边作等腰Rt△BCG,其中CB=CG,直线GA交y轴于点H,当C在x轴上A点右侧运动时,线段OH的长度是否发生变化?如果不变,求其值;如果变化,求线段OH的取值范围.
【解答】解:(1)①∵点A(6,0),点B(0,6),
∴OA=OB=6,
又∵∠AOB=90°,点M为AB的中点,
∴∠BOM=45°;
②∵BC⊥OD,
∴∠BEO=90°=∠AOB,
∴∠BOE+∠OBE=90°=∠BOE+∠DOA,
∴∠OBE=∠DOA,
∵OA=OB=6,AOB=90°,
∴∠OAB=45°=∠BOM,
在△OAD和△BOF中,
,
∴△OAD≌△BOF(ASA);
(2)线段OH的长度不会变化,OH=6,理由如下:
过G作GN⊥x轴,垂足为N.
∵∠BCG=90°,
∴∠BCO+∠GCN=90°.
∵∠AOB=∠GNC=90°,
∴∠BCO=∠CGN,∠CBO=∠GCN.
∵BC=CG,
∴△BCO≌△CGN(ASA),
∴GN=OC,CN=AO=BO,
∴OC=OA+AC=CN+AC=AN,
∴GN=AN,
∴∠GAN=45°=∠OAH.
∵∠AOH=90°,
∴△OAH是等腰直角三角形,
∴OA=OH=6.
∴无论P点怎么动,OH的长不变.
7.(2021秋 碑林区校级期中)【问题发现】
(1)如图①,将Rt△AOB置于平面直角坐标系中,直角顶点O与原点重合,点A落在x轴上,点B落在y轴上,已知A(4,0),B(0,3),C是x轴上一点,将Rt△AOB沿BC折叠,使点O落在AB边上的点D处,则点C的坐标为 (,0) .
【问题探究】
(2)如图②,将长方形OABC置于平面直角坐标系中,点A在y轴上,点C在x轴上,已知B(12,5),E是OA上一点,将长方形OABC沿CE折叠,点O恰好落在对角线AC上的点F处,求OF所在直线的函数表达式.
(3)如图③,将长方形OABC置于平面直角坐标系中,点A在y轴上,点C在x轴上,已知B(8,6),D在对角线AC上,且CD=OC,P是OD的中点,Q是OC上一点,将△OPQ沿PQ折叠,使点O落在AC边上的点E处,求点D的坐标及四边形OPEQ的面积.
【解答】解:(1)设OC为x,
∵A(4,0),B(0,3),
∴AB===5,
由翻折可知,DB=OB=3,OC=CD=x,
∴AD=2,
由勾股定理得,AD2+CD2=AC2,
即x2+22=(4﹣x)2,
解得x=,
∴点C的坐标为(,0),
故答案为:(,0);
(2)∵长方形OABC,点A在y轴上,点C在x轴上,B(12,5),
∴A(0,5),C(12,0),
设直线AC的解析式为y=kx+b,把A点和C点坐标代入得,
,
解得,
∴直线AC的解析式为y=﹣x+5,
由翻折可知,OC=CF=12,AF=1,
设OE=EF=y,
由勾股定理得,EF2+AF2=AE2,
即y2+12=(5﹣y)2,
解得y=2.4,
即OE=EF=2.4,
∴AE=2.6,
设点F的坐标为(m,﹣m+5),
∴×AF EF=AE yF,
即×1×2.4=×2.6m,
解得m=,
则点F的坐标为(,),
设直线OF的解析式为y=dx,代入F点坐标得,=d,
解得d=5,
∴直线OF的解析式为y=5x;
(3)连接OE,
∵P是OD的中点,
∴OP=PD,
由折叠可知,OP=PD=PE,OE⊥PQ,
∴∠POE=∠PEO,∠PED=∠PDE,
∴∠PEO+∠PED=90°,
∴OE⊥CD,
∴PQ∥CD,
∴Q是OC的中点,
∴三角形OPQ的面积是三角形OCD面积的四分之一,四边形OPEQ的面积是三角形OCD面积的二分之一,
∵B(8,6),
∴A(0,6),C(8,0),
∴AC===10,
∴OA OC=AC OE,
即×6×8=×10×OE,
解得OE=4.8,
∵OC=CD=8,
∴三角形OCD的面积为:CD OE=×8×4.8=19.2,
∴四边形OPEQ的面积是×19.2=9.6,
∵三角形OCD的面积为19.2,OC=8,
∴点D的纵坐标为19.2×2÷8=4.8,
设直线AC的解析式为y=nx+e,把A点和C点坐标代入得,,
解得,
∴直线AC的解析式为y=﹣x+6,
∵点D在直线AC上,当y=4.8时,4.8=﹣x+6,
解得x=1.6,
∴点D的坐标为(1.6,4.8).
8.(2021秋 和平区期中)如图1,直线y=x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)直线BC的函数表达式为 y=﹣x+3 ;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,请直接写出点P的坐标 (﹣,) ;
②若△PQB的面积为,请直接写出点M的坐标 (,0)或(﹣,0) ;
③若点K为线段OB的中点,连接CK,如图2,若在线段OC上有一点F,满足∠CKF=45°,请直接写出点F的坐标 (,0) .
【解答】解:(1)对于y=x+3,令x=0,y=3,
∴B(0,3),
令y=0,
∴x+3=0,
∴x=﹣6,
∴A(﹣6,0),
∵点C与点A关于y轴对称,
∴C(6,0),
设直线BC的解析式为y=kx+b,
∴,
∴,
∴直线BC的解析式为y=﹣x+3,
故答案为:y=﹣x+3;
(2)①设点M(m,0),
∴P(m,m+3),
∵B(0,3),C(6,0),
∴BC2=45,BM2=OM2+OB2=m2+9,MC2=(6﹣m)2,
∵∠MBC=90°,
∴△BMC是直角三角形,
∴BM2+BC2=MC2,
∴m2+9+45=(6﹣m)2,
∴m=﹣,
∴P(﹣,),
故答案为:(﹣,);
②设点M(n,0),
∵点P在直线AB:y=x+3上,
∴P(n,n+3),
∵点Q在直线BC:y=﹣x+3上,
∴Q(n,﹣n+3),
∴PQ=|n+3﹣(﹣n+3)|=|n|,
∵△PQB的面积为,
∴S△PQB=|n| |n|=n2=,
∴n=±,
∴M(,0)或(﹣,0),
故答案为:(,0)或(﹣,0);
③过点F作FH⊥FK交CK于H,过点H作HE⊥x轴于E,
∵∠CKF=45°,
∴△KFH是等腰直角三角形,
∴KF=FH,∠KFO+∠HFE=90°,
∵∠KFO+∠FKO=90°,
∴∠HFE=∠FKO,
∵∠KOF=∠FEH=90°,
∴△KOF≌△FEH(AAS),
∴EH=OF,EF=OK,
∵点K为线段OB的中点,OB=6,
∴EF=OK=,K(0,),
设F(x,0),则OE=x+,EH=OF=x,则H(x+,x),
∵C(6,0),K(0,),
设直线CK的解析式为y=kx+b,
∴,解得:,
∴直线CK的解析式为y=﹣x+,
∵点H在CK上,H(x+,x),
∴x=﹣(x+)+,解得:x=,
∴点F的坐标为(,0).
故答案为:(,0).
9.(2021秋 碑林区校级期中)如图,在平面直角坐标系中,直线y=x+6交x轴于点A,交y轴于点B,交直线y=﹣2x+9于点C.
(1)点C的坐标是 (1,7) .
(2)点M是直线AB上一点,点N是直线y=﹣2x+9上一点,连接线段MN,若MN∥x轴,且MN=6,求出所有符合条件的点M的坐标.
(3)在(2)的条件下,平面上是否存在点P,使得△BOP和△MNC全等,若存在,请直接写出点P的坐标,若不存在,请说明理由.
【解答】解:(1)解方程组,得,
所以点C的坐标为(1,7),
故答案为:(1,7);
(2)∵M是直线AB上一点,
设点M的坐标为(a,a+6),
∵MN∥x轴,点N是直线y=﹣2x+9上一点,
∴a+6=﹣2x+9,解得x=,
∴点N的坐标是(,a+6),
∵MN=6,
∴|﹣a|=6,解得:a=5或﹣3,
∴点M的坐标为(5,11)或(﹣3,3);
(3)存在,
①点M的坐标为(﹣3,3)时,点N的坐标为(3,3),
∴MN=6,MC==,NC==,
设点P的坐标为(x,y),
∵直线y=x+6交x轴于点A,交y轴于点B,
∴B(0,6),OB=6=MN,
当BP=NC,OP=MC时;
,解得:或,
∴点P的坐标为(4,4)或(﹣4,4),
当BP=MC,OP=NC时,
,解得:或,
∴点P的坐标为(4,2)或(﹣4,2),
②点M的坐标为(5,11)时,点N的坐标为(﹣1,11),
∴MN=6,MC==,NC==,
此时△MNC与①中的△MNC三边都对应相等,所以此时情况与①相同.
综上,点P的坐标为(4,4)或(﹣4,4)或(4,2)或(﹣4,2).
10.(2021秋 深圳期中)如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)填空:k= ;b= 4 ;m= 2 ;
(2)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由.
(3)若动点P在射线DC上从点D开始以每秒1个单位的速度运动,连接AP,设点P的运动时间为t秒.是否存在t的值,使△ACP和△ADP的面积比为1:3?若存在,直接写出t的值;若不存在,请说明理由.
【解答】解:(1)∵直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),
∴5=1+b,
∴b=4,
∴直线l2:y=﹣x+4,
∵直线l2:y=﹣x+4经过点C(2,m),
∴m=﹣2+4=2,
∴C(2,2),
把C(2,2)代入y=kx+1,得到k=.
∴k=,b=4,m=2.
故答案为:,4,2;
(2)作点C关于x轴的对称点C′,连接BC′交x轴于E,连接EC,则△BCE的周长最小.
∵B(﹣1,5),C′(2,﹣2),
∴直线BC′的解析式为y=﹣x+,
令y=0,得到x=,
∴E(,0),
∴存在一点E,使△BCE的周长最短,E(,0);
(3)∵点P在射线DC上从点D开始以每秒1个单位的速度运动,直线l1:y=x+1,
∴D(﹣2,0),
∵C(2,2),
∴CD==2,
∵点P的运动时间为t秒.
∴DP=t,
分两种情况:①点P在线段DC上,
∵△ACP和△ADP的面积比为1:3,
∴,
∴,
∴DP=×2=,
∴t=;
②点P在线段DC的延长线上,
∵△ACP和△ADP的面积比为1:3,
∴,
∴=,
∴DP=×2=3,
∴t=3.
综上:存在t的值,使△ACP和△ADP的面积比为1:3,t的值为或3.
11.(2021秋 开福区校级月考)已知直线AB交x轴于点A(a,o),交y轴于点B(0,b),且a、b满足|a+b|+(b﹣4)2=0.
(1)求∠ABO的度数;
(2)如图1,若点C在第一象限,且BE⊥AC于点E,延长BE至点D,使得BD=AC,连接OC、OD、CD,试判断△COD的形状,并说明理由;
(3)如图2,若点C在OB上,点F在AB的延长线上,且AC=CF,△ACP是以AC为直角边的等腰直角三角形,CQ⊥AF于点Q,求的值.
【解答】解:(1)∵|a+b|+(b﹣4)2=0,
∴a=﹣4,b=4,
∴点A的坐标为(﹣4,0),点B的坐标为(0,4),
∴AO=BO=4,
∵∠AOB=90°,
∴∠ABO的度数为45°;
(2)△COD是等腰直角三角形.
证明:如图1:
∵BE⊥AC,OA⊥OB,
∴∠EFB+∠EBF=∠OFA+∠OAF,
又∵∠OFA=∠EFB,
∴∠EBF=∠OAF,
在△AOC与△BOD中,
,
∴△AOC≌△BOD(SAS),
∴OC=OD,∠AOC=∠BOD,
∴∠AOB+∠BOC=∠BOC+∠DOC,
∴∠DOC=∠AOB=90°,
∴△COD为等腰直角三角形;
(3)过点C作CK⊥OB交AB于K,
∵∠ACP=90°,
∴∠BCP=∠OAC,
∵OA=OB,
∴∠OAC+∠CAF=∠OAB=45°,
∴∠OBA=∠F+∠BCF=45°,
∵AC=CF,
∴∠CAF=∠F,
∴∠BCF=∠OAC=∠BCP,即OB平分∠PCF,
∵△ACP是以AC为直角边的等腰直角三角形,
∴CA=CP,
∵AC=CF,
∴CP=CF,
∵CB=CB,
∴△BCF≌△BCP (SAS),
∴BF=BP,
∵∠OBA=45°,CK⊥OB,
∴△BCK为等腰直角三角形,
∴△ACF和△BCK均为等腰三角形,
∵CQ⊥AF,
∴FQ=AQ,BQ=QK,
∴BF=AK,
∵△BCK为等腰直角三角形,
∴BQ=QK=CQ,
∴===2.
12.(2021 南岗区校级开学)如图,直线y=x+6交x轴于A,交y轴于B,把△AOB绕着点O顺时针旋转,得到△COD,且点D在x轴正半轴上,延长AB交CD于点E.
(1)求直线CD的解析式;
(2)点P为线段DE上一点,连接PA、PB,设点P的横坐标为m,△PAB的面积为S,求S与m的函数解析式;
(3)在(2)的条件下,点Q为OD边上一点,若∠PQC=2∠OCQ,PQ+CQ=PA,求点P的坐标.
【解答】解:∵直线y=x+6交x轴于A,交y轴于B,
∴A(﹣12,0),B(0,6),
∴OA=12,OB=6,
∵把△AOB绕着点O顺时针旋转,得到△COD,
∴OC=OA=12,OD=OB=6,
∴C(0,12),D(6,0),
设直线CD的解析式为y=kx+b,
则,
解得:,
∴直线CD的解析式为y=﹣2x+12;
(2)如图1,∵点P在直线CD上且横坐标为m,
∴P(m,﹣2m+12),
设直线PA的解析式为y=ax+c,将P(m,﹣2m+12),A(﹣12,0)代入,
得:,
解得:,
∴直线PA的解析式为y=x+,
∵直线PA交y轴于点F,
∴F(0,),
∴OF=,
∴BF=OB﹣OF=6﹣=,
∴S△PAB=S△FAB+S△PBF=BF OA+BF xP=××(12+m)=15m﹣36,
∴S=15m﹣36;
(3)如图2,延长PQ交y轴于F,过点P作PH⊥x轴于点H,作PG⊥OC于点G,连接AF,
∵∠PQC=2∠OCQ,
∴180°﹣∠CQO﹣∠PQD=2(90°﹣∠CQO),
∴∠CQO=∠PQD,
∵∠FQO=∠PQD,
∴∠CQO=∠FQO,
∵∠COQ=∠FOQ=90°,OQ=OQ,
∴△COQ≌△FOQ(ASA),
∴OF=OC=12,QC=QF,
∵PQ+CQ=PA,
∴PQ+QF=PA,
即PF=PA,
∴∠PAF=∠PFA,
∵OA=OF=12,
∴∠OAF=∠OFA,
∴∠PAF﹣∠OAF=∠PFA﹣∠OFA,
即∠PAH=∠PFG,
∵∠PHA=∠PGF=90°,PA=PF,
∴△PHA≌△PGF(AAS),
∴PH=PG,
∴﹣2m+12=m,
解得:m=4,
∴P(4,4).
13.(2021春 黄陂区期末)如图,直线l1:y=kx﹣2k+1经过定点C,分别交x轴,y轴于A,B两点,直线l2经过O,C两点,点Dl2上.
(1)①直接写出点C的坐标为 (2,1) ;②求直线l2的解析式;
(2)如图1,若S△BOC=2S△BCD,求点D的坐标;
(3)如图2,直线l3经过D,E(0,﹣)两点,分别交x轴的正半轴、l1于点P,F,若PE=PF,∠EDO=45°,求k的值.
【解答】解(1)①∵y=kx﹣2k+1经过定点C,
∴点C的坐标与k的取值无关,
∴x=2时,y=1,
∴C(2,1),
故答案为:(2,1);
②设l2的解析式为:y=ax,
把C(2,1)代入y=ax得:a=,
∴l2的解析式为y=,
(2)如图,取OB的中点H,连接CH,
∵C(2,1),
∵S△BOC=2S△BCD,
当点D在线段OC上时,
则点D为OC的中点,
∴D(1,);
当点D在线段DC的延长线时,
∴S△BCD=,
即OB=,|xD|=3,
∴D(3,),
综上所述,符合条件的点D坐标为(1,)或(3,).
(3)过点C作CH∥EF,过点O作OH⊥OC,分别过点C,H作CM⊥OB于M,MN⊥OB于N,
∵∠EDO=45°,
∴∠OCH=45°,
∴OC=OH,
又∵∠MOC=∠NHO,∠OMC=∠ONH,
∴△COM≌△OHN(AAS),
∴CM=OH,OM=NH,
由C(2,1)得:H(1,﹣2),
∴yCH=3x﹣5,
由E(0,﹣)得:yEF=3x﹣,
∴P(,0),
过点F作FK⊥OA于K,
∵PF=PE,
∴△OPE≌△FPK(AAS),
∴F(1,),
将F(1,)代入l1:y=kx﹣2k+1,
∴k﹣2k+1=,
解得k=﹣.
14.(2021春 东港区校级期末)如图,在平面直角坐标系中,四边形OABC为矩形,点A、B的坐标分别为(12,0),(12,6),直线y=﹣x+b(b>0)与y轴交于点P,与边OA交于点D,与边BC交于点E.
(1)若直线y=﹣x+b(b>0)平分矩形OABC的面积,求b的值;
(2)在(1)的条件下,过点P的直线,与直线BC和x轴分别交于点N、M.问:是否存在ON平分∠CNM的情况?若存在,求线段DM的长,若不存在,请说明理由.
(3)将(1)中的直线沿y轴向下平移a个单位得到新直线l,矩形OABC沿平移后的直线折叠,若点O落在边BC上的F处,CF=9,求出a的值.
【解答】解:(1)∵直线y=﹣x+b(b>0)平分矩形OABC的面积,
∴直线过矩形的中心,
∵B(12,6),
∴矩形中心为(6,3),
∴﹣6+b=3,
解得b=12;
(2)如图,假设存在ON平分∠CNM的情况,
当PM与线段BC,OA交于N,M时,
过点O作OH⊥MN于H,
∵ON平分∠CNM,OC⊥BC,OH⊥MN,
∴OH=OC=6,
∵OP=12,
∴∠OPN=30°,
∴OM=OP=4,
当y=0时,﹣,解得x=8,
∴OD=8,
∴DM=OD﹣OM=8﹣4;
当PM与直线BC,OA交于N,M时,如图,
同理可得,此时DM=OD+OM=8+4,
综上:存在ON平分∠CNM的情况,此时DM=8﹣4或8+4;
(3)设平移后的直线y=﹣与y轴交于点P',沿此直线折叠,点O的对应点恰好落在BC边上F处,连接P'F,OF,
则有OP'=P'F=m,CP'=m﹣6,
在Rt△CP'F中,由勾股定理得:
(m﹣6)2+92=m2,
解得m=,
∴PP'=12﹣=,
∴a=.
15.(2021春 连山区期末)如图,矩形OABC在平面直角坐标系中,OA在x轴负半轴,OC在y轴正半轴,点D在边OC上,连接BD,将△BCD沿BD折叠,得到△BDE,使点E落在矩形OABC内部,过点E作EF⊥AB于F,直线CF交x轴于点M,若点E(﹣3,9),F恰为AB中点.
(1)如图1,直线CM的解析式;
(2)如图2,点P为x轴上的动点,过P作x轴的垂线,分别交直线CM、BD于点N、Q,若NQ=2CD,求点P坐标;
(3)点H为直线BD上动点,若△AEH以AE为直角边的直角三角形,是否存在点H?如果存在,直接写出点H坐标;不存在,请说明理由!
【解答】解:(1)延长FE交OC于点H,如图:
设OA=m,由折叠可知BC=BE=OA=m,
∵点E(﹣3,9),
∴AF=9,EH=3,EF=m﹣3,
∵F恰为AB中点,
∴BF=AF=9,OC=AB=18,
∴C(0,18),
在Rt△BEF中,由勾股定理得BE2=BF2+EF2,
∴m2=92+(m﹣3)2,
∴m=15,
∴F(﹣15,9),
设直线CM的解析式为y=kx+b,将C(0,18),F(﹣15,9)代入得:
,
解得,
∴直线CM解析式为:;
(2)如图:
设CD=n,则DE=n,DH=9﹣n,
在Rt△DEH中,DE2=DH2+EH2,
∴n2=(9﹣n)2+32,解得n=5,
∴CD=5,
∴OD=13,
∴D(0,13),
∵B(﹣15,18)
∴直线BD解析式为:
设P(t,0),则N(t,t+18),Q(t,﹣t+13),
∴NQ=|(t+18)﹣(﹣t+13)|=|t+5|,
∵NQ=2CD=10,
∴|t+5|=10,
解得t=或t=﹣,
∴P(,0)或P(﹣,0);
(3)存在,理由如下:
由(2)知直线BD为:,
设H(s,﹣s+13),而A(﹣15,0),E(﹣3,9),
∴AH2=(s+15)2+(﹣s+13)2,EH2=(s+3)2+(﹣s+4)2,AE2=122+(﹣9)2=225,
当EH为斜边时,EH2=AH2+AE2,
∴(s+3)2+(﹣s+4)2=(s+15)2+(﹣s+13)2+225,解得s=﹣33,
∴H(﹣33,24),
当AH为斜边时,AH2=EH2+AE2,
∴(s+15)2+(﹣s+13)2=(s+3)2+(﹣s+4)2+225,
解得s=﹣8,
∴H(﹣8,),
综上所述,H坐标为(﹣33,24)或(﹣8,).
16.(2021春 铁锋区期末)综合与探究.如图,在平面直角坐标系xOy中,直线AB与x轴,y轴分别交于点A(3,0)、点B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)直接写出AB的长 5 ;
(2)点C的坐标 (8,0) ,点D的坐标 D(0,﹣6) ;
(3)求直线AB的函数表达式;
(4)y轴上是否存在一点P,使得S△PAB=S△OCD?若存在,直接写出点P的坐标;若不存在,请说明理由.
【解答】解:(1)∵A(3,0)、B(0,4),
∴OA=3,OB=4,
∵∠AOB=90°,
∴AB=;
故答案为:5;
(2)设直线AB的表达式为y=kx+b,将A(3,0)、B(0,4)代入,
得:,
解得:,
∴直线AB的表达式为y=﹣x+4;
(3)由折叠得:AC=AB=5,
∴OC=OA+AC=3+5=8,
∴点C的坐标为(8,0),
设点D(0,m),则OD=﹣m,
由折叠得CD=BD=4﹣m,
在Rt△OCD中,OC2+OD2=CD2,
∴82+(﹣m)2=(4﹣m)2,
解得:m=﹣6,
∴D(0,﹣6),
故答案为:C(8,0),D(0,﹣6);
(4)存在,设点P(0,n),
∴PB=|n﹣4|,
∵S△PAB=S△OCD,
∴PB OA=××OC×OD,
即|n﹣4|×3=××8×6,
解得:n=12或﹣4,
∴P(0,12)或(0,﹣4).
17.(2021春 集贤县期末)如图1,平面直角坐标系中,直线y=kx+b与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4).
(1)求点C的坐标及直线AB的表达式;
(2)如图2,在x轴上有一点E,过点E作直线l⊥x轴,交直线y=2x于点F,交直线y=kx+b于点G,若GF的长为3,求点E的坐标;
(3)在y轴上是否存在一点M,使以O、C、M为顶点的三角形是等腰三角形,若存在,直接写出点M的坐标;若不存在,说明理由.
【解答】解:(1)∵点C在直线y=2x上,
∴2a=4,
解得a=2,
∴C(2,4);
将A(6,0),C(2,4)代入直线y=kx+b,得:
,
解得,
∴直线AB的解析式为:y=﹣x+6;
(2)根据题意设E点坐标为(m,0),
∵点E、F、G三点在同一直线上,且点F在直线y=2x上,点G在y=﹣x+6上,
∴F(m,2m),G(m,﹣m+6),
又∵|FG|=3,
∴|2m﹣(﹣m+6)|=3,
解得m=3或m=1,
∴E点的坐标为(3,0)或(1,0);
(3)存在,
设M(0,t),
∵C(2,4),
∴OC==2,OM=|t|,CM==,
要使以O、C、M为顶点的三角形是等腰三角形,分以下三种情况:
①当OC=OM时,
即|t|=2,
解得t=±2,
∴M(0,2)或(0,﹣2);
②当OC=CM时,
即=2,
解得t=8或t=0(舍去),
∴M(0,8);
③当CM=OM时,
即=|t|,
解得t=,
∴M(0,);
综上,符合条件的M点的坐标是(0,2)或(0,﹣2)或(0,8)或(0,).
18.(2021春 天心区期末)我们知道一次函数y=mx+n与y=﹣mx+n(m≠0)的图象关于y轴对称,所以我们定义:函数y=mx+n与y=﹣mx+n(m≠0)互为“M”函数.
(1)请直接写出函数y=2x+5的“M”函数;
(2)如果一对“M”函数y=mx+n与y=﹣mx+n(m≠0)的图象交于点A,且与x轴交于B,C两点,如图所示,若∠BAC=90°,且△ABC的面积是8,求这对“M”函数的解析式;
(3)在(2)的条件下,若点D是y轴上的一个动点,当△ABD为等腰三角形时,请求出点D的坐标.
【解答】(1)解:根据互为“M”函数的定义,
∴函数y=2x+5的“M”函数为y=﹣2x+5;
(2)解:根据题意,y=mx+n 和 y=﹣mx+n 为一对“M函数”.
∴AB=AC,
又∵∠BAC=90°,
∴△ABC 为等腰直角三角形,
∴∠ABC=∠ACB=45°,
∵OB=OC,
∴∠BAO=∠CAO=45°,
∴OA=OB=OC,
又∵ 且 BC=2AO,
∴,
∵A、B、C是一次函数y=mx+n与y=﹣mx+n(m≠0)的图象于坐标轴的交点,
∴A(0,n),B(﹣,0),C(,0),
∵OA=OB=n,
∴=2,
∴m=1,
∴ 和 ;
(3)解:根据等腰三角形的性质,分情况,
∵,
∴AB=4,
由(2)知,A(0,2),B(﹣2,0),C(2,0),
∴①以 A 为顶点,则 AB=AD,
当点D在点A上方时,AD=2+4,
当点D在点A下方时,AD=2﹣4,
∴D1(0,2+4),D2(0,2﹣4),
②以 B 为顶点,则 BA=BD,
此时点D在y轴负半轴,
∴D3(0,﹣2),
③以 D 为顶点,则 DA=DB,
此时D为坐标原点,
∴D4(0,0).
∴D点坐标为 D1(0,2+4),D2(0,2﹣4),D3(0,﹣2),∴D4(0,0).
19.(2021春 洪泽区期末)如图,直线y=﹣x+12与x轴交于点A(12,0),与直线OB交于点B(8,4),x轴上一点P从O点出发以每秒2个单位的速度向终点A运动,作PE⊥x轴交OB于E,过E作EF∥x轴且EF=PE,以PE、EF为边作矩形PEFG,设运动时间为t.
(1)当点F落在直线AB上时,求t的值;
(2)在运动过程中,设矩形PEFG与△ABO的重叠部分面积为S,求S与t的关系式,并写出相应的t的取值范围;
(3)矩形PEFG的对角线交于点Q,直接写出PQ+AQ的最小值为 .
【解答】解:(1)如图1,设直线OB的解析式为y=kx,
∵点B(8,4)在直线y=kx上,
∴8k=4,
解得,k=,
∴y=x,
∵OP=2t,
∴P(2t,0),E(2t,t),
∵EF=PE=t,
∴F(t,t),G(t,0),
当点F落在直线AB上时,则t+12=t,解得t=.
(2)当点E与点B重合时,则2t=8,解得t=4;
当点G与点A重合时,则t=12,解得t=;
当点P与点A重合时,则2t=12,解得t=6,
当0<t≤时,如图1,PE=t,EF=t,
∴S=t t=t2;
当<t≤4时,如图2,设直线y=﹣x+12交y轴于点C,则C(0,12),
∴OA=OC=12,
∵∠AOC=90°,
∴∠OAC=∠OCA=45°,
设EF、FG分别交AB于点J、点K,则∠FKJ=∠OCA=45°,∠FJK=∠OAC=45°,
∴JF=FK;
对于y=﹣x+12,当x=t时,y=t+12,
∴K(t,t+12),
∴FK=t﹣(t+12)=t﹣12,
∴S=t2﹣(t﹣12)2=t2+42t﹣72;
当4<t≤时,如图3,∠GKA=∠PJA=∠OAC=45°,
∴PA=PJ=12﹣2t,GA=GK=12t,
∴S=(12﹣2t)2(12t)2=t2+6t;
当<t≤6时,如图4,S=(12﹣2t)2=2t2﹣24t+72,
综上所述,S=.
(3)如图4,连接AE、GE,由矩形的性质可知,点Q在GE上,且PQ=EQ,
∴PQ+AQ=EQ+AQ≥AE,
∴当点Q落在AE上,且AE最小时,PQ+AQ的值最小;
如图5,点G与点A重合,则AE与GE重合,
∴点Q在AE上,
∴PQ+AQ=AE,
此时t=,
∴OP=2t=2×=,
∴AP=12﹣=,
∴PE=2×=,
∴AE==;
作BD⊥x轴于点D,作AE′⊥OB于点E′,则OB==4,
由S△OAB=×OB AE′=OA BD,得×AE′=×12×4,解得AE′=,
∴AE=AE′,
∴AE的长就是点A到直线OB的距离,
∴AE⊥OB,
∴AE的值最小,此时PQ+AQ的值最小,为,
故答案为:.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
