2021-2022学年人教五四新版九年级上册数学期中复习试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年人教五四新版九年级上册数学期中复习试卷(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 453.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 08:34:02 | ||
图片预览


文档简介
2021-2022学年人教五四新版九年级上册数学期中复习试卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列各数中,是无理数的是( )
A. B. C. D.3.1415
2.下列运算正确的是( )
A.(﹣2a3)2=4a6 B.a2 a3=a6
C.3a+a2=3a3 D.(a﹣b)2=a2﹣b2
3.一个正多边形绕它的中心旋转45°后,就与原正多边形第一次重合,那么这个正多边形( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
4.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )
A. B. C.2 D.
5.如图,AB为⊙O的直径,点C为⊙O上的一点,过点C作⊙O的切线,交直径AB的延长线于点D;若∠A=23°,则∠D的度数是( )
A.23° B.44° C.46° D.57°
6.某校八年级组织一次篮球赛,各班均组队参赛,赛制为单循环形式(每两班之间都赛一场),共需安排15场比赛,则八年级班级的个数为( )
A.5 B.6 C.7 D.8
7.若分式+2的值为0,则x的值为( )
A.±2 B.2 C.﹣2 D.0
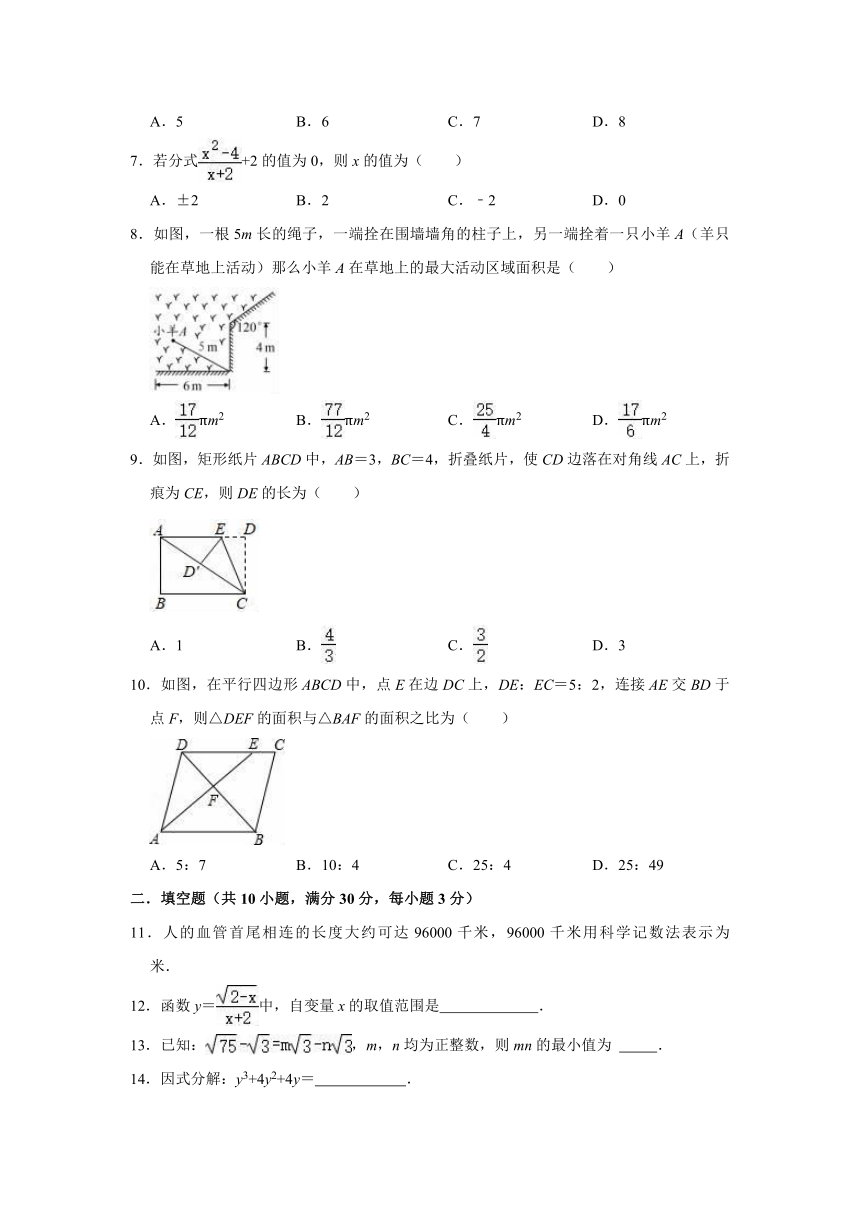
8.如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )
A.πm2 B.πm2 C.πm2 D.πm2
9.如图,矩形纸片ABCD中,AB=3,BC=4,折叠纸片,使CD边落在对角线AC上,折痕为CE,则DE的长为( )
A.1 B. C. D.3
10.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=5:2,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.5:7 B.10:4 C.25:4 D.25:49
二.填空题(共10小题,满分30分,每小题3分)
11.人的血管首尾相连的长度大约可达96000千米,96000千米用科学记数法表示为 米.
12.函数y=中,自变量x的取值范围是 .
13.已知:,m,n均为正整数,则mn的最小值为 .
14.因式分解:y3+4y2+4y= .
15.请写出一个图象在第二、四象限的反比例函数的表达式: .
16.如果不等式组的解集是x>3,那么m的取值范围是 .
17.⊙O的半径为2cm,则⊙O的内接正方形的面积是 cm2.
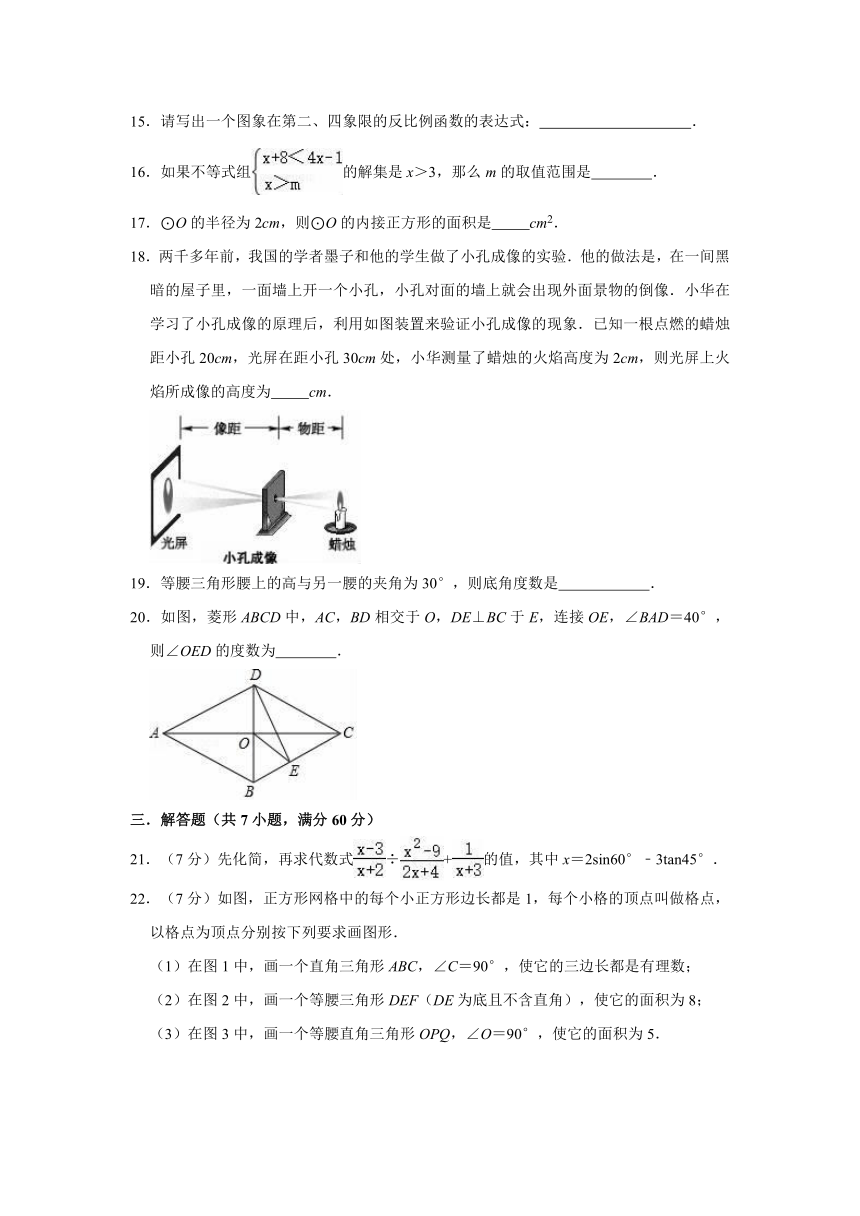
18.两千多年前,我国的学者墨子和他的学生做了小孔成像的实验.他的做法是,在一间黑暗的屋子里,一面墙上开一个小孔,小孔对面的墙上就会出现外面景物的倒像.小华在学习了小孔成像的原理后,利用如图装置来验证小孔成像的现象.已知一根点燃的蜡烛距小孔20cm,光屏在距小孔30cm处,小华测量了蜡烛的火焰高度为2cm,则光屏上火焰所成像的高度为 cm.
19.等腰三角形腰上的高与另一腰的夹角为30°,则底角度数是 .
20.如图,菱形ABCD中,AC,BD相交于O,DE⊥BC于E,连接OE,∠BAD=40°,则∠OED的度数为 .
三.解答题(共7小题,满分60分)
21.(7分)先化简,再求代数式÷+的值,其中x=2sin60°﹣3tan45°.
22.(7分)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图形.
(1)在图1中,画一个直角三角形ABC,∠C=90°,使它的三边长都是有理数;
(2)在图2中,画一个等腰三角形DEF(DE为底且不含直角),使它的面积为8;
(3)在图3中,画一个等腰直角三角形OPQ,∠O=90°,使它的面积为5.
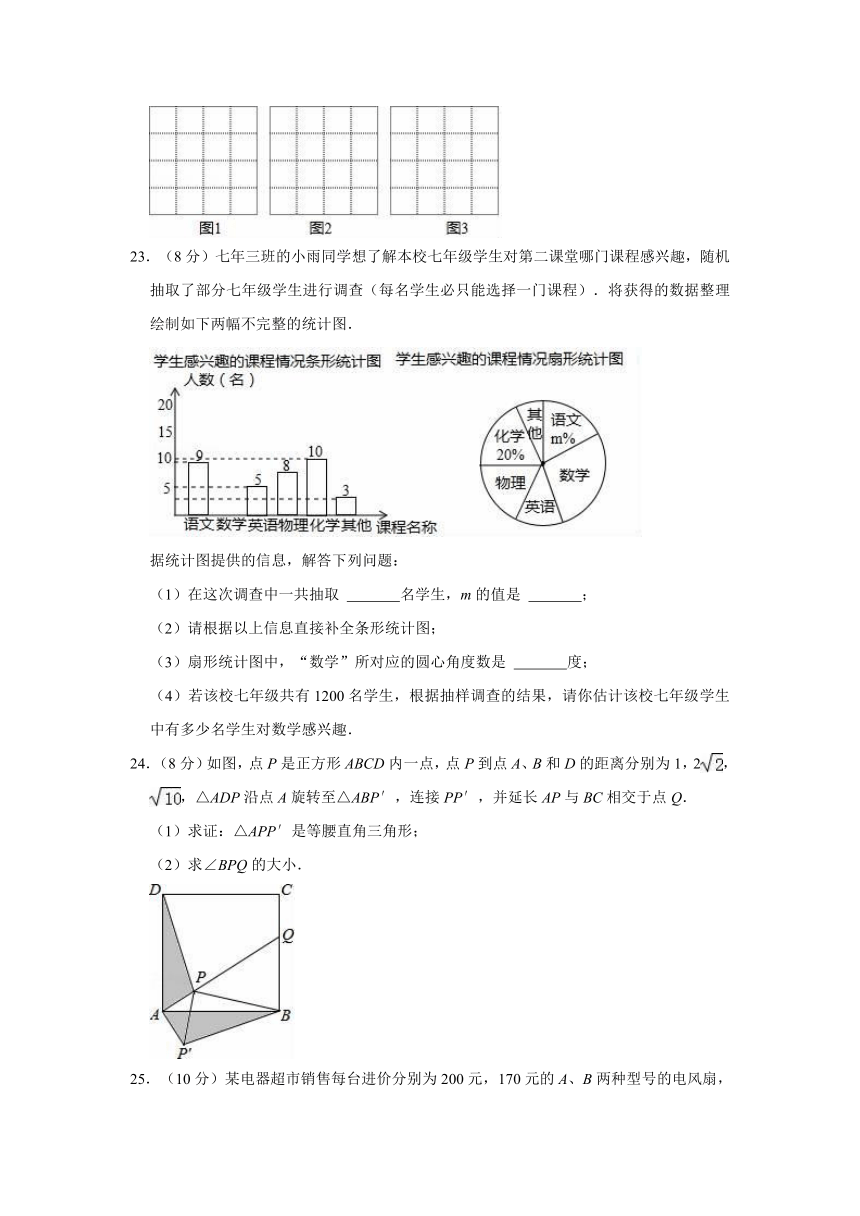
23.(8分)七年三班的小雨同学想了解本校七年级学生对第二课堂哪门课程感兴趣,随机抽取了部分七年级学生进行调查(每名学生必只能选择一门课程).将获得的数据整理绘制如下两幅不完整的统计图.
据统计图提供的信息,解答下列问题:
(1)在这次调查中一共抽取 名学生,m的值是 ;
(2)请根据以上信息直接补全条形统计图;
(3)扇形统计图中,“数学”所对应的圆心角度数是 度;
(4)若该校七年级共有1200名学生,根据抽样调查的结果,请你估计该校七年级学生中有多少名学生对数学感兴趣.
24.(8分)如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2,,△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.
25.(10分)某电器超市销售每台进价分别为200元,170元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 3台 5台 1800元
第二周 4台 10台 3100元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
26.(10分)定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到这边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连接AD,若AD2=BD CD,则称点D是△ABC中BC边上的“好点”.
(1)如图2,点D是△ABC中BC边上的“好点”,且∠BAC=90°,∠C=30°,AC=4,则BD= ;
(2)△ABC中,BC=14,tanB=,tanC=1,点D是BC边上的“好点”,求线段BD的长;
(3)如图3,△ABC是⊙O的内接三角形,点H在AB上,连接CH并延长交⊙O于点D.若点H是△BCD中CD边上的“好点”.
①求证:OH⊥AB;
②若OH∥BD,⊙O的半径为R,且R=3OH,求的值.
27.(10分)(1)如图1,在四边形ABCD中,已知AD∥BC,点M是CD的中点,连接AM并延长交BC的延长线于点E,若S四边形ABCD=10,那么S△ABE= .
(2)如图2,已知,锐角∠AOB内有一点M,过点M作直线l分别交OA,OB于点P、Q,将直线l绕点M旋转时,发现:当点M恰好是PQ中点时,S△OPQ最小,请证明这个结论.
(3)如图3,已知在直角坐标系中,OA是第一象限的角分线,∠MOx=30°,且OM=3,过点M作直线l交OA于点P,交x轴正半轴于点Q,求S△OPQ的最小值及此时直线l的表达式.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、是无理数,故此选项正确;
B、=2是整数,是有理数,故此选项错误;
C、是分数,是有理数,故此选项错误;
D、3.1415是有限小数,是有理数,故此选项错误.
故选:A.
2.解:(﹣2a3)2=4a6,故A正确;
a2 a3=a5,故B错误;
3a与a2不是同类项,不能合并,故C错误;
(a﹣b)2=a2﹣2ab+b2,故D选项错误;
故选:A.
3.解:∵一个正多边形绕着它的中心旋转45°后,能与原正多边形重合,
360°÷45°=8,
∴这个正多边形是正八边形.
正八边形既是轴对称图形,又是中心对称图形.
故选:C.
4.解:连接BD.
则BD=,AD=2,
则tanA===.
故选:D.
5.解:连接OC,如图,
∵CD为⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
∵∠COD=2∠A=46°,
∴∠D=90°﹣46°=44°.
故选:B.
6.解:设八年级有x个班,
依题意得: x(x﹣1)=15,
整理得:x2﹣x﹣30=0,
解得:x1=6,x2=﹣5(不合题意,舍去).
故选:B.
7.解:∵ +2=0,
∴x2﹣4+2x+4=0.
即x2+2x=0.
∴(x+2)x=0.
∴x1=﹣2,x2=0.
当x=﹣2时,分式的分母为0,分式无意义.
所以x=0
故选:D.
8.解:大扇形的圆心角是90度,半径是5,
所以面积==π(m2);
小扇形的圆心角是180°﹣120°=60°,半径是1m,
则面积==(m2),
则小羊A在草地上的最大活动区域面积=π+=π(m2).
故选:B.
9.解:在矩形ABCD中,AB=3,AD=4,
∴∠A=∠D=90°,DC=AB=3,
∴AC===5,
由折叠的性质得:∠CD'E=∠D=90°D'C=DC=3,DE=D'E,
∴∠AD'E=90°,AD'=AC﹣CD'=5﹣3=2,
设DE=x,则D'E=x,AE=4﹣x,
在Rt△AED'中:AD'2+ED'2=AE2,
即22+x2=(4﹣x)2,
解得:x=,
即DE=,
故选:C.
10.解:设DE=5k,EC=2k,则CD=7k,
∵四边形ABCD是平行四边形,
∴AB=CD=7k,DE∥AB,
∴△DEF∽△BAF,
∴===,
故选:D.
二.填空题(共10小题,满分30分,每小题3分)
11.解:96000千米=96000000=9.6×107(米).
故答案为:9.6×107.
12.解:根据题意,得:,
解得:x≤2且x≠﹣2,
故答案为:x≤2且x≠﹣2.
13.解:原式=5﹣=m﹣n,
∵m,n均为正整数,
∴n的最小值为1,此时m最小值为5,
∴mn的最小值为5×1=5,
故答案为:5.
14.解:原式=y(y2+4y+4)=y(y+2)2,
故答案为:y(y+2)2.
15.解:∵图象在第二、四象限,
∴y=﹣,
故答案为:y=﹣.
16.解:在中
由①得,x>3
由②得,x>m
根据已知条件,不等式组解集是x>3
根据“同大取大”原则m≤3.
故答案为:m≤3.
17.解:如图所示:
∵四边形ABCD是⊙O的内接正方形,
∴∠BAD=∠ABC=90°,BD=AC,
∴BD、AC是直径,
∵⊙O的半径为2cm,
∴BD=AC=2×2=4(cm),
∴正方形ABCD的面积=AC BD=×4×4=8(cm2),
故答案为:8.
18.解:如图,OE=20cm,OF=30cm,AB=2cm,
∵AB∥CD,
∴△OAB∽△OCD,
∴=,即=,
∴CD=3(cm),
即光屏上火焰所成像的高度为3cm.
19.解:如图,分两种情况:
①在左图中,AB=AC,BD⊥AC,∠ABD=30°,
∴∠A=60°,
∴∠C=∠ABC==60°;
②在右图中,AB=AC,BD⊥AC,∠ABD=30°,
∴∠DAB=60°,∠BAC=120°,
∴∠C=∠ABC==30°.
故答案为30°或60°.
20.解:∵四边形ABCD是菱形,∠BAD=40°,
∴∠DAO=BAD=20°,AC⊥BD,DO=BO,AD∥BC,
∴∠DOA=90°,
∴∠ADO=90°﹣∠DAO=70°,
∵AD∥BC,DE⊥BC,
∴DE⊥AD,
∴∠ADE=90°,
∴∠ODE=∠AD∠E﹣∠ADO=20°,
∵DE⊥BC,
∴∠DEB=90°,
∵DO=BO,
∴OE=BD=OD,
∴∠OED=∠ODE=20°,
故答案为:20°.
三.解答题(共7小题,满分60分)
21.解:原式=×+=.
∵x=2sin60°﹣3tan45°=2×﹣3×1=﹣3,
∴原式==.
22.解:(1)如图1中,△ABC即为所求作.
(2)如图2中,△DEF即为所求作.
(3)如图3中,△OPQ即为所求作.
23.解:(1)在这次调查中一共抽取学生10÷20%=50(名),m%=×100%=18%,即m=18;
故答案为:50、18;
(2)选择数学课程的人数为50﹣(9+5+8+10+3)=15(名),
补全图形如下:
(3)扇形统计图中,“数学”所对应的圆心角度数是360°×=108°,
故答案为:108;
(4)1200×=360(名),
答:估计该校七年级学生中有360名学生对数学感兴趣.
24.(1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵△ADP沿点A旋转至△ABP′,
∴AP=AP′,∠PAP′=∠DAB=90°,
∴△APP′是等腰直角三角形;
(2)解:∵△APP′是等腰直角三角形,
∴PP′=PA=,∠APP′=45°,
∵△ADP沿点A旋转至△ABP′,
∴PD=P′B=,
在△PP′B中,PP′=,PB=2,P′B=,
∵()2+(2)2=()2,
∴PP′2+PB2=P′B2,
∴△PP′B为直角三角形,∠P′PB=90°,
∴∠BPQ=180°﹣∠APP′﹣∠P′PB=180°﹣45°﹣90°=45°.
25.解:(1)设A、B两种型号电风扇的销售单价分别为x元、y元,
依题意得:,
解得:,
答:A、B两种型号电风扇的销售单价分别为250元、210元;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30﹣a)台.
依题意得:200a+170(30﹣a)≤5400,
解得:a≤10.
答:超市最多采购A种型号电风扇10台时,采购金额不多于5400元;
(3)依题意有:(250﹣200)a+(210﹣170)(30﹣a)=1400,
解得:a=20,
∵a≤10,
∴在(2)的条件下超市不能实现利润1400元的目标.
26.解:(1)如图1,
当AD⊥BC时,
∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,
∵∠BAC=90°,
∴∠B+∠C=90°,
∴∠BAD=∠C,
∴△ABD∽△CAD,
∴,
∴AD2=BD CD,
∴D是BC边上的“好点”,
在Rt△ABC 中,∠C=30°,AC=4,
∴AB=4 tan30°=,
在Rt△ABD中,∠BAD=∠C=30°,
∴BD=AB=,
故答案是;
(2)如图2,
作AE⊥BC于E,
在Rt△ABE中,tanB==,
∴设AE=3a,BE=4a,
在Rt△ACE中,∠C=45°,
∵tan45°=,
∵CE=AE=3a,
∴3a+4a=14,
∴a=2,
∴AE=CE=6,BE=8,
∴AB=10,
设BD=x,
∴DE=8﹣x,
在Rt△ADE中,由勾股定理得,
AD2=DE2+AE2=(8﹣x)2+62,
∵点D是BC边上的“好点”,
∴AD2=BD CD=x (14﹣x),
∴x (14﹣x)=(8﹣x)2+62,
∴x1=5,x2=10,
即BD=5或10;
(3)如图3,
①证明:∵点H是△BCD中CD边上的“好点”,
∴BH2=CH HD,
∵∠CAB=∠CBD,∠ACD=∠ABD,
∴△ACH∽△DBH,
∴=,
∴CH HD=AH BH,
∴BH2=AH BH,
∴AH=BH,
∴OH⊥AB;
②连接AD,
设OH=a,则OA=3a,,
由①知,OH⊥AB,
又∵OH∥BD,
∴BD⊥AB,
∴∠ABD=90°,
∴AD是⊙O的直径,
∴OA=OD=3a,
在Rt△AOH 中,由勾股定理得,
AH=2,
∵AH=BH=2,OA=OD,
∴BD=2a,
在Rt△BDH中,由勾股定理得,
DH==2a,
由BH2=CH DH得,
(2)2=CH (2),
∴CH=a,
∴==;
27.解:(1)∵AD∥BC,
∴∠ADE=∠FCE,
在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA),
∴S△ADE=S△FCE,
∴S四边形ABCD=S四边形ABCE+S△ADE=S四边形ABCE+S△FCE=S△ABF,
∵S四边形ABCD=10,
∴S△ABE=10,
故答案为:10.
(2)过点M作EF交AO于点E,交BO于点F,过点P作PG∥OB交EF于点G,如答图1.
设MF<ME,由(1)可得,
当M为PQ中点时,可证明△MPG≌△MQF.
∴S四边形POFG=S△OPQ,
∵S四边形POFG<S△EOF,
∴S△OPQ<S△EOF.
故结论得证.
(3)由(2)可知,当点M为PQ中点时,S△OPQ值最小.
过点M作MR⊥x轴于点R,过点P作PS⊥x轴于点S,如答图2.
∵∠MOx=30°,OM=3.
∴MR=OM=,
OR=cos30° OM=.
∴点M坐标为(,).
∵MQ∥PS,
∴△MQR∽△PQS,
∴,
∴PS=2MR=3.
又直线OA表达式为y=x,把y=3代入得x=3,
∴点P坐标为(3,3).
设直线l的表达式为y=kx+b,
∴,解得.
∴直线l的表达式为y=(2+)x﹣3﹣3.
令y=0,则x=3﹣3.
即OQ=3﹣3.
∴S△OPQ= OQ PS
=
=.
故S△OPQ的面积最小为,此时直线l的表达式为y=(2+)x﹣3﹣3.
一.选择题(共10小题,满分30分,每小题3分)
1.下列各数中,是无理数的是( )
A. B. C. D.3.1415
2.下列运算正确的是( )
A.(﹣2a3)2=4a6 B.a2 a3=a6
C.3a+a2=3a3 D.(a﹣b)2=a2﹣b2
3.一个正多边形绕它的中心旋转45°后,就与原正多边形第一次重合,那么这个正多边形( )
A.是轴对称图形,但不是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.既是轴对称图形,又是中心对称图形
D.既不是轴对称图形,也不是中心对称图形
4.如图,将△ABC放在每个小正方形的边长为1的网格中,点A,B,C均在格点上,则tanA的值是( )
A. B. C.2 D.
5.如图,AB为⊙O的直径,点C为⊙O上的一点,过点C作⊙O的切线,交直径AB的延长线于点D;若∠A=23°,则∠D的度数是( )
A.23° B.44° C.46° D.57°
6.某校八年级组织一次篮球赛,各班均组队参赛,赛制为单循环形式(每两班之间都赛一场),共需安排15场比赛,则八年级班级的个数为( )
A.5 B.6 C.7 D.8
7.若分式+2的值为0,则x的值为( )
A.±2 B.2 C.﹣2 D.0
8.如图,一根5m长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动)那么小羊A在草地上的最大活动区域面积是( )
A.πm2 B.πm2 C.πm2 D.πm2
9.如图,矩形纸片ABCD中,AB=3,BC=4,折叠纸片,使CD边落在对角线AC上,折痕为CE,则DE的长为( )
A.1 B. C. D.3
10.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=5:2,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A.5:7 B.10:4 C.25:4 D.25:49
二.填空题(共10小题,满分30分,每小题3分)
11.人的血管首尾相连的长度大约可达96000千米,96000千米用科学记数法表示为 米.
12.函数y=中,自变量x的取值范围是 .
13.已知:,m,n均为正整数,则mn的最小值为 .
14.因式分解:y3+4y2+4y= .
15.请写出一个图象在第二、四象限的反比例函数的表达式: .
16.如果不等式组的解集是x>3,那么m的取值范围是 .
17.⊙O的半径为2cm,则⊙O的内接正方形的面积是 cm2.
18.两千多年前,我国的学者墨子和他的学生做了小孔成像的实验.他的做法是,在一间黑暗的屋子里,一面墙上开一个小孔,小孔对面的墙上就会出现外面景物的倒像.小华在学习了小孔成像的原理后,利用如图装置来验证小孔成像的现象.已知一根点燃的蜡烛距小孔20cm,光屏在距小孔30cm处,小华测量了蜡烛的火焰高度为2cm,则光屏上火焰所成像的高度为 cm.
19.等腰三角形腰上的高与另一腰的夹角为30°,则底角度数是 .
20.如图,菱形ABCD中,AC,BD相交于O,DE⊥BC于E,连接OE,∠BAD=40°,则∠OED的度数为 .
三.解答题(共7小题,满分60分)
21.(7分)先化简,再求代数式÷+的值,其中x=2sin60°﹣3tan45°.
22.(7分)如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图形.
(1)在图1中,画一个直角三角形ABC,∠C=90°,使它的三边长都是有理数;
(2)在图2中,画一个等腰三角形DEF(DE为底且不含直角),使它的面积为8;
(3)在图3中,画一个等腰直角三角形OPQ,∠O=90°,使它的面积为5.
23.(8分)七年三班的小雨同学想了解本校七年级学生对第二课堂哪门课程感兴趣,随机抽取了部分七年级学生进行调查(每名学生必只能选择一门课程).将获得的数据整理绘制如下两幅不完整的统计图.
据统计图提供的信息,解答下列问题:
(1)在这次调查中一共抽取 名学生,m的值是 ;
(2)请根据以上信息直接补全条形统计图;
(3)扇形统计图中,“数学”所对应的圆心角度数是 度;
(4)若该校七年级共有1200名学生,根据抽样调查的结果,请你估计该校七年级学生中有多少名学生对数学感兴趣.
24.(8分)如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2,,△ADP沿点A旋转至△ABP′,连接PP′,并延长AP与BC相交于点Q.
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小.
25.(10分)某电器超市销售每台进价分别为200元,170元的A、B两种型号的电风扇,表中是近两周的销售情况:
销售时段 销售数量 销售收入
A种型号 B种型号
第一周 3台 5台 1800元
第二周 4台 10台 3100元
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
26.(10分)定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到这边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连接AD,若AD2=BD CD,则称点D是△ABC中BC边上的“好点”.
(1)如图2,点D是△ABC中BC边上的“好点”,且∠BAC=90°,∠C=30°,AC=4,则BD= ;
(2)△ABC中,BC=14,tanB=,tanC=1,点D是BC边上的“好点”,求线段BD的长;
(3)如图3,△ABC是⊙O的内接三角形,点H在AB上,连接CH并延长交⊙O于点D.若点H是△BCD中CD边上的“好点”.
①求证:OH⊥AB;
②若OH∥BD,⊙O的半径为R,且R=3OH,求的值.
27.(10分)(1)如图1,在四边形ABCD中,已知AD∥BC,点M是CD的中点,连接AM并延长交BC的延长线于点E,若S四边形ABCD=10,那么S△ABE= .
(2)如图2,已知,锐角∠AOB内有一点M,过点M作直线l分别交OA,OB于点P、Q,将直线l绕点M旋转时,发现:当点M恰好是PQ中点时,S△OPQ最小,请证明这个结论.
(3)如图3,已知在直角坐标系中,OA是第一象限的角分线,∠MOx=30°,且OM=3,过点M作直线l交OA于点P,交x轴正半轴于点Q,求S△OPQ的最小值及此时直线l的表达式.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、是无理数,故此选项正确;
B、=2是整数,是有理数,故此选项错误;
C、是分数,是有理数,故此选项错误;
D、3.1415是有限小数,是有理数,故此选项错误.
故选:A.
2.解:(﹣2a3)2=4a6,故A正确;
a2 a3=a5,故B错误;
3a与a2不是同类项,不能合并,故C错误;
(a﹣b)2=a2﹣2ab+b2,故D选项错误;
故选:A.
3.解:∵一个正多边形绕着它的中心旋转45°后,能与原正多边形重合,
360°÷45°=8,
∴这个正多边形是正八边形.
正八边形既是轴对称图形,又是中心对称图形.
故选:C.
4.解:连接BD.
则BD=,AD=2,
则tanA===.
故选:D.
5.解:连接OC,如图,
∵CD为⊙O的切线,
∴OC⊥CD,
∴∠OCD=90°,
∵∠COD=2∠A=46°,
∴∠D=90°﹣46°=44°.
故选:B.
6.解:设八年级有x个班,
依题意得: x(x﹣1)=15,
整理得:x2﹣x﹣30=0,
解得:x1=6,x2=﹣5(不合题意,舍去).
故选:B.
7.解:∵ +2=0,
∴x2﹣4+2x+4=0.
即x2+2x=0.
∴(x+2)x=0.
∴x1=﹣2,x2=0.
当x=﹣2时,分式的分母为0,分式无意义.
所以x=0
故选:D.
8.解:大扇形的圆心角是90度,半径是5,
所以面积==π(m2);
小扇形的圆心角是180°﹣120°=60°,半径是1m,
则面积==(m2),
则小羊A在草地上的最大活动区域面积=π+=π(m2).
故选:B.
9.解:在矩形ABCD中,AB=3,AD=4,
∴∠A=∠D=90°,DC=AB=3,
∴AC===5,
由折叠的性质得:∠CD'E=∠D=90°D'C=DC=3,DE=D'E,
∴∠AD'E=90°,AD'=AC﹣CD'=5﹣3=2,
设DE=x,则D'E=x,AE=4﹣x,
在Rt△AED'中:AD'2+ED'2=AE2,
即22+x2=(4﹣x)2,
解得:x=,
即DE=,
故选:C.
10.解:设DE=5k,EC=2k,则CD=7k,
∵四边形ABCD是平行四边形,
∴AB=CD=7k,DE∥AB,
∴△DEF∽△BAF,
∴===,
故选:D.
二.填空题(共10小题,满分30分,每小题3分)
11.解:96000千米=96000000=9.6×107(米).
故答案为:9.6×107.
12.解:根据题意,得:,
解得:x≤2且x≠﹣2,
故答案为:x≤2且x≠﹣2.
13.解:原式=5﹣=m﹣n,
∵m,n均为正整数,
∴n的最小值为1,此时m最小值为5,
∴mn的最小值为5×1=5,
故答案为:5.
14.解:原式=y(y2+4y+4)=y(y+2)2,
故答案为:y(y+2)2.
15.解:∵图象在第二、四象限,
∴y=﹣,
故答案为:y=﹣.
16.解:在中
由①得,x>3
由②得,x>m
根据已知条件,不等式组解集是x>3
根据“同大取大”原则m≤3.
故答案为:m≤3.
17.解:如图所示:
∵四边形ABCD是⊙O的内接正方形,
∴∠BAD=∠ABC=90°,BD=AC,
∴BD、AC是直径,
∵⊙O的半径为2cm,
∴BD=AC=2×2=4(cm),
∴正方形ABCD的面积=AC BD=×4×4=8(cm2),
故答案为:8.
18.解:如图,OE=20cm,OF=30cm,AB=2cm,
∵AB∥CD,
∴△OAB∽△OCD,
∴=,即=,
∴CD=3(cm),
即光屏上火焰所成像的高度为3cm.
19.解:如图,分两种情况:
①在左图中,AB=AC,BD⊥AC,∠ABD=30°,
∴∠A=60°,
∴∠C=∠ABC==60°;
②在右图中,AB=AC,BD⊥AC,∠ABD=30°,
∴∠DAB=60°,∠BAC=120°,
∴∠C=∠ABC==30°.
故答案为30°或60°.
20.解:∵四边形ABCD是菱形,∠BAD=40°,
∴∠DAO=BAD=20°,AC⊥BD,DO=BO,AD∥BC,
∴∠DOA=90°,
∴∠ADO=90°﹣∠DAO=70°,
∵AD∥BC,DE⊥BC,
∴DE⊥AD,
∴∠ADE=90°,
∴∠ODE=∠AD∠E﹣∠ADO=20°,
∵DE⊥BC,
∴∠DEB=90°,
∵DO=BO,
∴OE=BD=OD,
∴∠OED=∠ODE=20°,
故答案为:20°.
三.解答题(共7小题,满分60分)
21.解:原式=×+=.
∵x=2sin60°﹣3tan45°=2×﹣3×1=﹣3,
∴原式==.
22.解:(1)如图1中,△ABC即为所求作.
(2)如图2中,△DEF即为所求作.
(3)如图3中,△OPQ即为所求作.
23.解:(1)在这次调查中一共抽取学生10÷20%=50(名),m%=×100%=18%,即m=18;
故答案为:50、18;
(2)选择数学课程的人数为50﹣(9+5+8+10+3)=15(名),
补全图形如下:
(3)扇形统计图中,“数学”所对应的圆心角度数是360°×=108°,
故答案为:108;
(4)1200×=360(名),
答:估计该校七年级学生中有360名学生对数学感兴趣.
24.(1)证明:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∵△ADP沿点A旋转至△ABP′,
∴AP=AP′,∠PAP′=∠DAB=90°,
∴△APP′是等腰直角三角形;
(2)解:∵△APP′是等腰直角三角形,
∴PP′=PA=,∠APP′=45°,
∵△ADP沿点A旋转至△ABP′,
∴PD=P′B=,
在△PP′B中,PP′=,PB=2,P′B=,
∵()2+(2)2=()2,
∴PP′2+PB2=P′B2,
∴△PP′B为直角三角形,∠P′PB=90°,
∴∠BPQ=180°﹣∠APP′﹣∠P′PB=180°﹣45°﹣90°=45°.
25.解:(1)设A、B两种型号电风扇的销售单价分别为x元、y元,
依题意得:,
解得:,
答:A、B两种型号电风扇的销售单价分别为250元、210元;
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(30﹣a)台.
依题意得:200a+170(30﹣a)≤5400,
解得:a≤10.
答:超市最多采购A种型号电风扇10台时,采购金额不多于5400元;
(3)依题意有:(250﹣200)a+(210﹣170)(30﹣a)=1400,
解得:a=20,
∵a≤10,
∴在(2)的条件下超市不能实现利润1400元的目标.
26.解:(1)如图1,
当AD⊥BC时,
∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,
∵∠BAC=90°,
∴∠B+∠C=90°,
∴∠BAD=∠C,
∴△ABD∽△CAD,
∴,
∴AD2=BD CD,
∴D是BC边上的“好点”,
在Rt△ABC 中,∠C=30°,AC=4,
∴AB=4 tan30°=,
在Rt△ABD中,∠BAD=∠C=30°,
∴BD=AB=,
故答案是;
(2)如图2,
作AE⊥BC于E,
在Rt△ABE中,tanB==,
∴设AE=3a,BE=4a,
在Rt△ACE中,∠C=45°,
∵tan45°=,
∵CE=AE=3a,
∴3a+4a=14,
∴a=2,
∴AE=CE=6,BE=8,
∴AB=10,
设BD=x,
∴DE=8﹣x,
在Rt△ADE中,由勾股定理得,
AD2=DE2+AE2=(8﹣x)2+62,
∵点D是BC边上的“好点”,
∴AD2=BD CD=x (14﹣x),
∴x (14﹣x)=(8﹣x)2+62,
∴x1=5,x2=10,
即BD=5或10;
(3)如图3,
①证明:∵点H是△BCD中CD边上的“好点”,
∴BH2=CH HD,
∵∠CAB=∠CBD,∠ACD=∠ABD,
∴△ACH∽△DBH,
∴=,
∴CH HD=AH BH,
∴BH2=AH BH,
∴AH=BH,
∴OH⊥AB;
②连接AD,
设OH=a,则OA=3a,,
由①知,OH⊥AB,
又∵OH∥BD,
∴BD⊥AB,
∴∠ABD=90°,
∴AD是⊙O的直径,
∴OA=OD=3a,
在Rt△AOH 中,由勾股定理得,
AH=2,
∵AH=BH=2,OA=OD,
∴BD=2a,
在Rt△BDH中,由勾股定理得,
DH==2a,
由BH2=CH DH得,
(2)2=CH (2),
∴CH=a,
∴==;
27.解:(1)∵AD∥BC,
∴∠ADE=∠FCE,
在△ADE与△FCE中,
,
∴△ADE≌△FCE(ASA),
∴S△ADE=S△FCE,
∴S四边形ABCD=S四边形ABCE+S△ADE=S四边形ABCE+S△FCE=S△ABF,
∵S四边形ABCD=10,
∴S△ABE=10,
故答案为:10.
(2)过点M作EF交AO于点E,交BO于点F,过点P作PG∥OB交EF于点G,如答图1.
设MF<ME,由(1)可得,
当M为PQ中点时,可证明△MPG≌△MQF.
∴S四边形POFG=S△OPQ,
∵S四边形POFG<S△EOF,
∴S△OPQ<S△EOF.
故结论得证.
(3)由(2)可知,当点M为PQ中点时,S△OPQ值最小.
过点M作MR⊥x轴于点R,过点P作PS⊥x轴于点S,如答图2.
∵∠MOx=30°,OM=3.
∴MR=OM=,
OR=cos30° OM=.
∴点M坐标为(,).
∵MQ∥PS,
∴△MQR∽△PQS,
∴,
∴PS=2MR=3.
又直线OA表达式为y=x,把y=3代入得x=3,
∴点P坐标为(3,3).
设直线l的表达式为y=kx+b,
∴,解得.
∴直线l的表达式为y=(2+)x﹣3﹣3.
令y=0,则x=3﹣3.
即OQ=3﹣3.
∴S△OPQ= OQ PS
=
=.
故S△OPQ的面积最小为,此时直线l的表达式为y=(2+)x﹣3﹣3.
同课章节目录
