第二章 机械振动 章末综合复习(课件)(35张PPT)-2021-2022学年【扬帆起航系列】人教版(2019)高中物理课件选择性必修第一册
文档属性
| 名称 | 第二章 机械振动 章末综合复习(课件)(35张PPT)-2021-2022学年【扬帆起航系列】人教版(2019)高中物理课件选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-09 09:01:54 | ||
图片预览







文档简介
(共35张PPT)
人教版(2019)高中物理选择性必修第一册
第二章 机械振动
章 末 复 习
授课人:扬帆起航
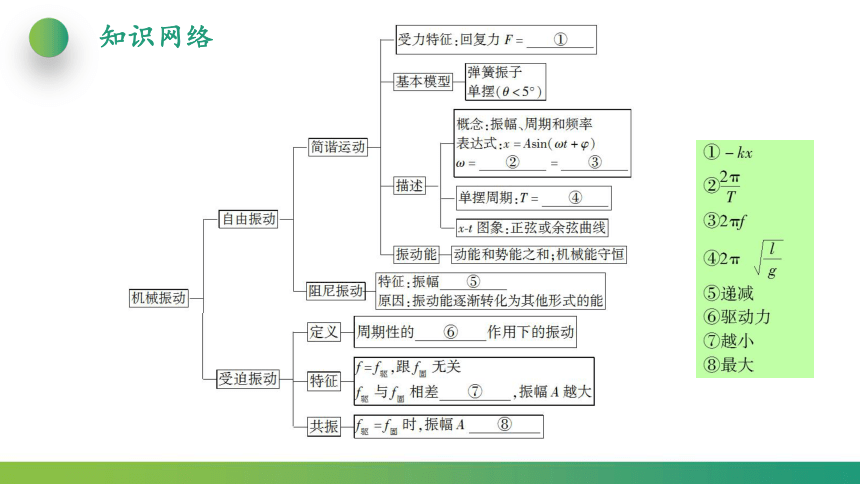
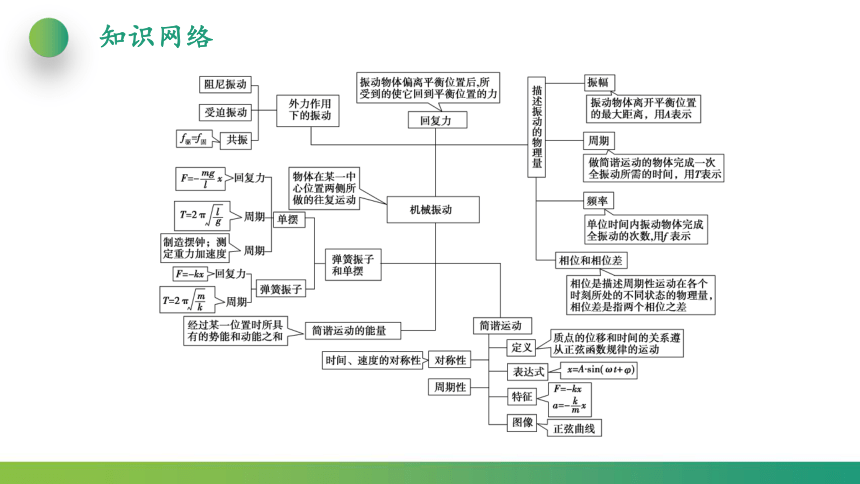
知识网络
知识网络
01
命题点一 简谐运动
机械振动
(1)定义:物体在跟位移大小成正比并且总是指向平衡位置的回复力作用下的振动.
(2)平衡位置:物体在振动过程中回复力为零的位置.
(3)回复力
①定义:使物体返回到平衡位置的力.
②方向:总是指向平衡位置。
③来源:属于效果力,可以是某一个力,也可以是几个力的合力或某个力的分力。
简谐运动
(4)简谐运动的特征
①动力学特征:F回=-kx.
②运动学特征:x、v、a 均按正弦或余弦规律发生周期性变化(注意v、a的变化趋势相反).
③能量特征:系统的机械能守恒,振幅A不变.
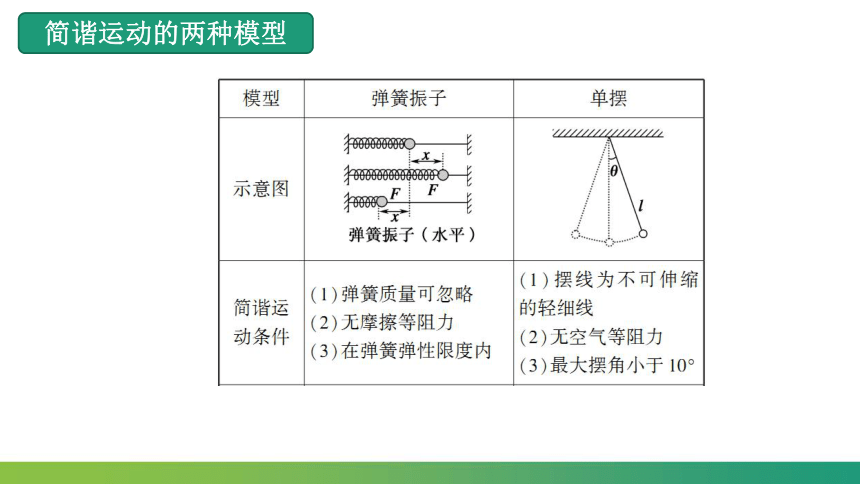
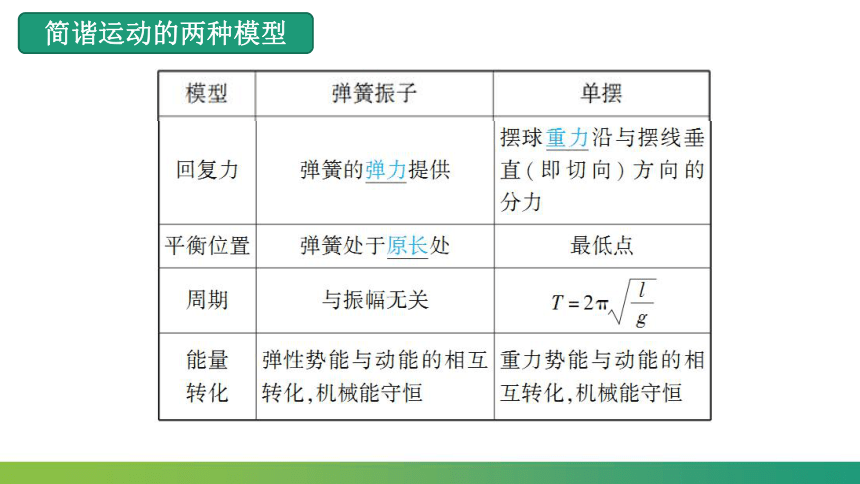
简谐运动的两种模型
简谐运动的两种模型
02
命题点二 简谐运动的描述
机械振动
(1)动力学表达式:F=-kx,其中“-”表示回复力与位移的方向相反.
(2)运动学表达式:x=Asin(ωt+φ),其中A代表振幅,ω=2πf表示简谐运动的快慢.
简谐运动的表达式
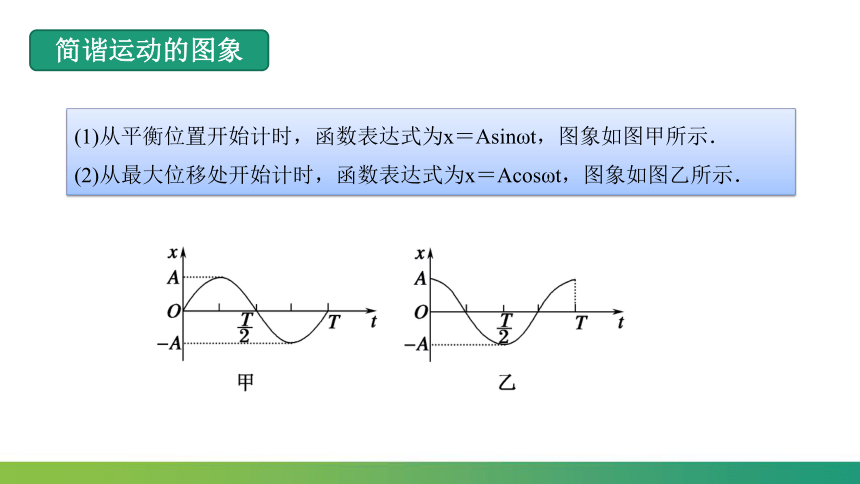
(1)从平衡位置开始计时,函数表达式为x=Asinωt,图象如图甲所示.
(2)从最大位移处开始计时,函数表达式为x=Acosωt,图象如图乙所示.
简谐运动的图象
对简谐运动图象的认识
(1)简谐运动的图象是一条正弦或余弦曲线,如图所示.
(2)图象反映的是位移随时间的变化规律,随时间的增加而延伸,不代表质点运动的轨迹.
简谐运动的图象
(1)由图象可以得出质点做简谐运动的振幅、周期和频率.
(2)可以确定某时刻质点离开平衡位置的位移.
(3)可以确定某时刻质点回复力、加速度的方向:因回复力总是指向平衡位置,故回复力和加速度的方向在图象上总是指向t轴.
图象信息
(4)确定某时刻质点速度的方向:速度的方向可以通过下一时刻位移的变化来判定,若下一时刻位移增加,振动质点的速度方向就是远离t轴,若下一时刻位移减小,振动质点的速度方向就是指向t轴.
(5)比较不同时刻回复力、加速度的大小.
(6)比较不同时刻质点的动能、势能的大小.
6.比较各时刻质点的加速度的方向和大小:在图中,t1时刻质点位移x1为正,加速度a1为负,两者方向相反;t2时刻质点位移x2为负,加速度a2为正,又因为|x1|>|x2|,所以|a1|>|a2|.
7.比较不同时刻质点的势能、动能的大小:质点的位移越大,它所具有的势能越大,动能则越小.如图所示,在t1时刻质点的势能Ep1大于t2时刻质点的势能Ep2,而动能Ek1从简谐运动的振动图像可以知道振动物体的运动情况
F=-kx,“-”表示回复力的方向与位移方向相反,k是比例系数,不一定是弹簧的劲度系数.
简谐运动的加速度与物体偏离平衡位置的位移成正比而方向相反,为变加速运动,远离平衡位置时,x、F、a、Ep均增大,v、Ek均减小,衡位置时则相反.
动力学特征
运动学特征
相隔 或 的两个时刻,振子处于同一位置且振动状态相同.
(1)相隔或(n为正整数)的两个时刻,振子位置关于平衡位置对称,位移、速度、加速度大小相等,方向相反.
(2)如图所示,振子经过关于平衡位置O对称的两点P、P′(OP=OP′)时,速度的大小、动能、势能相等,相对于平衡位置的位移大小相等.
运动的周期性特征
对称性特征
(3)振子由P到O所用时间等于由O到P′所用时间,即tPO=tOP′.
(4)振子往复过程中通过同一段路程(如OP段)所用时间相等,即tOP=tPO.
振动的能量包括动能Ek和势能Ep,简谐运动过程中,系统动能与势能相互转化,系统的机械能守恒.
对称性特征
能量特征
03
命题点三 单摆
机械振动
(1)回复力:摆球重力沿切线方向的分力,F回=-mgsinθ= =-kx,负号表示回复力F回与位移x的方向相反.
(2)向心力:细线的拉力和重力沿细线方向的分力的合力充当向心力,F向=FT-mgcosθ.两点说明:当摆球在最高点时,F向= =0,FT=mgcosθ.当摆球在最低点时,F向= ,F向最大,FT=mg+m
对单摆的理解
周期公式T=2π 的两点说明
(1)l为等效摆长,表示从悬点到摆球重心的距离;
(2)g为当地重力加速度.
实验原理与操作
用单摆测定重力加速度
①数据处理
a.公式法:算出重力加速度g的值,再算出g的平均值.
b.图象法:作出l T2图象求g值.
数据处理与分析
产生原因 减小方法
偶然误差 测量时间(单摆周期)及摆长时产生误差 ①多次测量再求平均值
②计时从单摆经过平衡位置时开始
系统误差 主要来源于单摆模型本身 ①摆球要选体积小,密度大的
②最大摆角要小于10°
误差分析
04
命题点四
受迫振动和共振
机械振动
自由振动、受迫振动和共振的关系比较
共振曲线:如图所示,横坐标为驱动力频率f,纵坐标为振幅A.它直观地反映了驱动力频率对某固有频率为f0的振动系统受迫振动振幅的影响,由图可知,f与f0越接近,振幅A越大;当f=f0时,振幅A最大.
受迫振动中系统能量的转化:做受迫振动的系统的机械能不守恒,系统与外界时刻进行能量交换.
对共振的理解
1、(单选)一位游客在千岛湖边欲乘坐游船,当日风浪较大,游船上下浮动.可把游船浮动简化成竖直方向的简谐运动,振幅为20 cm,周期为3.0 s.当船上升到最高点时,甲板刚好与码头地面平齐.地面与甲板的高度差不超过10 cm时,游客能舒服地登船.在一个周期内,游客能舒服登船的时间是( )
A.0.5 s B.0.75 s
C.1.0 s D.1.5 s
C
课堂巩固
【答案】:C
【解析】:从平衡位置开始计时,游船的振动方程为x=20sin cm,游客要舒服地登船需满足的条件Δx=20-x≤10,解得0.25 s≤t≤1.25 s,故游客能舒服地登船的时间Δt=1.0 s,选项C正确.
2、(多选)如图,轻弹簧上端固定,下端连接一小物块,物块沿竖直方向做简谐运动.以竖直向上为正方向,物块简谐运动的表达式为y=0.1sin(2.5πt)m.t=0时刻,一小球从距物块h高处自由落下;t=0.6 s时,小球恰好与物块处于同一高度.取重力加速度的大小g=10 m/s2.以下判断正确的是( )
A.h=1.7 m
B.简谐运动的周期是0.8 s
C.0.6 s内物块运动的路程为0.2 m
D.t=0.4 s时,物块与小球运动方向相反
AB
课堂巩固
【答案】:AB
【解析】:由物块做简谐运动的表达式y=0.1sin(2.5πt)m知,ω=2.5π,T= = s=0.8 s,选项B正确;t=0.6 s时,y=-0.1 m,对小球:h+|y|= gt2,解得h=1.7 m,选项A正确;物块0.6 s内运动的路程为0.3 m,t=0.4 s时,物块经过平衡位置向下运动,与小球运动方向相同.故选项C、D错误.
3、(多选)如图所示,为半径很大的光滑圆弧轨道上的一小段,小球B静止在圆弧轨道的最低点O处,另有一小球A自圆弧轨道上C处由静止滚下,经时间t与B发生正碰. 碰后两球分别在这段圆弧轨道上运动而未离开轨道.当两球第二次相碰时
( )
A.相间隔的时间为4t
B.相间隔的时间为2t
C.将仍在O处相碰
D.可能在O点以外的其他地方相碰
E.两球在碰撞的瞬间水平方向上的动量守恒
BCE
课堂巩固
【答案】:BCE
【解析】:小球的运动可视为简谐运动.由单摆振动周期公式T=2π (此处l即为圆弧轨道半径)知,两球周期相同,碰撞后应同时回到平衡位置,即只能在平衡位置处相碰.又由振动的周期性知,两次相碰的间隔时间为2t,综上讨论可知,选项B、C正确;两球在O点相碰,水平方向上合力为零,遵循动量守恒,故选项E正确.
4、(多选)正在运转的机器,当其飞轮以角速度ω0匀速转动时,机器的振动不强烈,切断电源,飞轮的转动逐渐慢下来,在某一小段时间内机器却发生了强烈的振动,此后飞轮转速继续变慢,机器的振动也随之减弱,在机器停下来之后若重新启动机器,使飞轮转动的角速度从0较缓慢地增大到ω0,在这一过程中( )
A.机器不一定还会发生强烈的振动
B.机器一定还会发生强烈的振动
C.若机器发生强烈振动,强烈振动可能发生在飞轮角速度为ω0时
D.若机器发生强烈振动,强烈振动时飞轮的角速度肯定不为ω0
BD
课堂巩固
【答案】:BD
【解析】:从以角速度ω0转动逐渐慢下来,在某一小段时间内机器却发生了强烈的振动,说明此过程机器的固有频率与驱动频率相等达到了共振,当飞轮转动的角速度从0较缓
慢地增大到ω0,在这一过程中,一定会出现机器的固有频率与驱动频率相等即达到共振的现象,机器一定还会发生强烈的振动,故A错误,B正确;由已知当机器的飞轮以角速度ω0匀速转动时,其振动不强烈,则机器若发生强烈振动,强烈振动时飞轮的角速度肯定不为ω0,故C错误,D正确.
人教版(2019)高中物理选择性必修第一册
第二章 机械振动
章 末 复 习
授课人:扬帆起航
知识网络
知识网络
01
命题点一 简谐运动
机械振动
(1)定义:物体在跟位移大小成正比并且总是指向平衡位置的回复力作用下的振动.
(2)平衡位置:物体在振动过程中回复力为零的位置.
(3)回复力
①定义:使物体返回到平衡位置的力.
②方向:总是指向平衡位置。
③来源:属于效果力,可以是某一个力,也可以是几个力的合力或某个力的分力。
简谐运动
(4)简谐运动的特征
①动力学特征:F回=-kx.
②运动学特征:x、v、a 均按正弦或余弦规律发生周期性变化(注意v、a的变化趋势相反).
③能量特征:系统的机械能守恒,振幅A不变.
简谐运动的两种模型
简谐运动的两种模型
02
命题点二 简谐运动的描述
机械振动
(1)动力学表达式:F=-kx,其中“-”表示回复力与位移的方向相反.
(2)运动学表达式:x=Asin(ωt+φ),其中A代表振幅,ω=2πf表示简谐运动的快慢.
简谐运动的表达式
(1)从平衡位置开始计时,函数表达式为x=Asinωt,图象如图甲所示.
(2)从最大位移处开始计时,函数表达式为x=Acosωt,图象如图乙所示.
简谐运动的图象
对简谐运动图象的认识
(1)简谐运动的图象是一条正弦或余弦曲线,如图所示.
(2)图象反映的是位移随时间的变化规律,随时间的增加而延伸,不代表质点运动的轨迹.
简谐运动的图象
(1)由图象可以得出质点做简谐运动的振幅、周期和频率.
(2)可以确定某时刻质点离开平衡位置的位移.
(3)可以确定某时刻质点回复力、加速度的方向:因回复力总是指向平衡位置,故回复力和加速度的方向在图象上总是指向t轴.
图象信息
(4)确定某时刻质点速度的方向:速度的方向可以通过下一时刻位移的变化来判定,若下一时刻位移增加,振动质点的速度方向就是远离t轴,若下一时刻位移减小,振动质点的速度方向就是指向t轴.
(5)比较不同时刻回复力、加速度的大小.
(6)比较不同时刻质点的动能、势能的大小.
6.比较各时刻质点的加速度的方向和大小:在图中,t1时刻质点位移x1为正,加速度a1为负,两者方向相反;t2时刻质点位移x2为负,加速度a2为正,又因为|x1|>|x2|,所以|a1|>|a2|.
7.比较不同时刻质点的势能、动能的大小:质点的位移越大,它所具有的势能越大,动能则越小.如图所示,在t1时刻质点的势能Ep1大于t2时刻质点的势能Ep2,而动能Ek1
F=-kx,“-”表示回复力的方向与位移方向相反,k是比例系数,不一定是弹簧的劲度系数.
简谐运动的加速度与物体偏离平衡位置的位移成正比而方向相反,为变加速运动,远离平衡位置时,x、F、a、Ep均增大,v、Ek均减小,衡位置时则相反.
动力学特征
运动学特征
相隔 或 的两个时刻,振子处于同一位置且振动状态相同.
(1)相隔或(n为正整数)的两个时刻,振子位置关于平衡位置对称,位移、速度、加速度大小相等,方向相反.
(2)如图所示,振子经过关于平衡位置O对称的两点P、P′(OP=OP′)时,速度的大小、动能、势能相等,相对于平衡位置的位移大小相等.
运动的周期性特征
对称性特征
(3)振子由P到O所用时间等于由O到P′所用时间,即tPO=tOP′.
(4)振子往复过程中通过同一段路程(如OP段)所用时间相等,即tOP=tPO.
振动的能量包括动能Ek和势能Ep,简谐运动过程中,系统动能与势能相互转化,系统的机械能守恒.
对称性特征
能量特征
03
命题点三 单摆
机械振动
(1)回复力:摆球重力沿切线方向的分力,F回=-mgsinθ= =-kx,负号表示回复力F回与位移x的方向相反.
(2)向心力:细线的拉力和重力沿细线方向的分力的合力充当向心力,F向=FT-mgcosθ.两点说明:当摆球在最高点时,F向= =0,FT=mgcosθ.当摆球在最低点时,F向= ,F向最大,FT=mg+m
对单摆的理解
周期公式T=2π 的两点说明
(1)l为等效摆长,表示从悬点到摆球重心的距离;
(2)g为当地重力加速度.
实验原理与操作
用单摆测定重力加速度
①数据处理
a.公式法:算出重力加速度g的值,再算出g的平均值.
b.图象法:作出l T2图象求g值.
数据处理与分析
产生原因 减小方法
偶然误差 测量时间(单摆周期)及摆长时产生误差 ①多次测量再求平均值
②计时从单摆经过平衡位置时开始
系统误差 主要来源于单摆模型本身 ①摆球要选体积小,密度大的
②最大摆角要小于10°
误差分析
04
命题点四
受迫振动和共振
机械振动
自由振动、受迫振动和共振的关系比较
共振曲线:如图所示,横坐标为驱动力频率f,纵坐标为振幅A.它直观地反映了驱动力频率对某固有频率为f0的振动系统受迫振动振幅的影响,由图可知,f与f0越接近,振幅A越大;当f=f0时,振幅A最大.
受迫振动中系统能量的转化:做受迫振动的系统的机械能不守恒,系统与外界时刻进行能量交换.
对共振的理解
1、(单选)一位游客在千岛湖边欲乘坐游船,当日风浪较大,游船上下浮动.可把游船浮动简化成竖直方向的简谐运动,振幅为20 cm,周期为3.0 s.当船上升到最高点时,甲板刚好与码头地面平齐.地面与甲板的高度差不超过10 cm时,游客能舒服地登船.在一个周期内,游客能舒服登船的时间是( )
A.0.5 s B.0.75 s
C.1.0 s D.1.5 s
C
课堂巩固
【答案】:C
【解析】:从平衡位置开始计时,游船的振动方程为x=20sin cm,游客要舒服地登船需满足的条件Δx=20-x≤10,解得0.25 s≤t≤1.25 s,故游客能舒服地登船的时间Δt=1.0 s,选项C正确.
2、(多选)如图,轻弹簧上端固定,下端连接一小物块,物块沿竖直方向做简谐运动.以竖直向上为正方向,物块简谐运动的表达式为y=0.1sin(2.5πt)m.t=0时刻,一小球从距物块h高处自由落下;t=0.6 s时,小球恰好与物块处于同一高度.取重力加速度的大小g=10 m/s2.以下判断正确的是( )
A.h=1.7 m
B.简谐运动的周期是0.8 s
C.0.6 s内物块运动的路程为0.2 m
D.t=0.4 s时,物块与小球运动方向相反
AB
课堂巩固
【答案】:AB
【解析】:由物块做简谐运动的表达式y=0.1sin(2.5πt)m知,ω=2.5π,T= = s=0.8 s,选项B正确;t=0.6 s时,y=-0.1 m,对小球:h+|y|= gt2,解得h=1.7 m,选项A正确;物块0.6 s内运动的路程为0.3 m,t=0.4 s时,物块经过平衡位置向下运动,与小球运动方向相同.故选项C、D错误.
3、(多选)如图所示,为半径很大的光滑圆弧轨道上的一小段,小球B静止在圆弧轨道的最低点O处,另有一小球A自圆弧轨道上C处由静止滚下,经时间t与B发生正碰. 碰后两球分别在这段圆弧轨道上运动而未离开轨道.当两球第二次相碰时
( )
A.相间隔的时间为4t
B.相间隔的时间为2t
C.将仍在O处相碰
D.可能在O点以外的其他地方相碰
E.两球在碰撞的瞬间水平方向上的动量守恒
BCE
课堂巩固
【答案】:BCE
【解析】:小球的运动可视为简谐运动.由单摆振动周期公式T=2π (此处l即为圆弧轨道半径)知,两球周期相同,碰撞后应同时回到平衡位置,即只能在平衡位置处相碰.又由振动的周期性知,两次相碰的间隔时间为2t,综上讨论可知,选项B、C正确;两球在O点相碰,水平方向上合力为零,遵循动量守恒,故选项E正确.
4、(多选)正在运转的机器,当其飞轮以角速度ω0匀速转动时,机器的振动不强烈,切断电源,飞轮的转动逐渐慢下来,在某一小段时间内机器却发生了强烈的振动,此后飞轮转速继续变慢,机器的振动也随之减弱,在机器停下来之后若重新启动机器,使飞轮转动的角速度从0较缓慢地增大到ω0,在这一过程中( )
A.机器不一定还会发生强烈的振动
B.机器一定还会发生强烈的振动
C.若机器发生强烈振动,强烈振动可能发生在飞轮角速度为ω0时
D.若机器发生强烈振动,强烈振动时飞轮的角速度肯定不为ω0
BD
课堂巩固
【答案】:BD
【解析】:从以角速度ω0转动逐渐慢下来,在某一小段时间内机器却发生了强烈的振动,说明此过程机器的固有频率与驱动频率相等达到了共振,当飞轮转动的角速度从0较缓
慢地增大到ω0,在这一过程中,一定会出现机器的固有频率与驱动频率相等即达到共振的现象,机器一定还会发生强烈的振动,故A错误,B正确;由已知当机器的飞轮以角速度ω0匀速转动时,其振动不强烈,则机器若发生强烈振动,强烈振动时飞轮的角速度肯定不为ω0,故C错误,D正确.
