人教版(2019)高中数学选修三 6.1分类加法计数原理与分步乘法计数原理 课件(20张)
文档属性
| 名称 | 人教版(2019)高中数学选修三 6.1分类加法计数原理与分步乘法计数原理 课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 09:29:24 | ||
图片预览








文档简介
(共20张PPT)
第六章 记数原理
6.1 分类加法计数原理与分步乘法计数原理
新课引入
问题1 用一个大写的英文字母或一个阿拉伯数字给教室
里的一个座位编号,总共能编出多少种不同的号码?
新课引入
问题2 用一个大写的英文字母和一个阿拉伯数字给教室
里的一个座位编号,总共能编出多少种不同的号码?
课堂探究
问题1 用一个大写的英文字母或一个阿拉伯数字给教室
里的一个座位编号,总共能编出多少种不同的号码?
问题2 用一个大写的英文字母和一个阿拉伯数字给教室
里的一个座位编号,总共能编出多少种不同的号码?
36种
260种
这两个问题有什么区别?
完成一件事有两类不同方案,在第1类方案中有m种不同的
方法,在第2类方案中有n种不同的方法,那么完成这件事
共有多少种不同的方法?
这个叫分类加法计数原理
思考:有n类不同方案了?
课堂探究
用前6个大写的英文字母和1~9个阿拉伯数字,以A1, A2,…A9,B1,B2,…的方式给教室里的一个座位编号,总共能编出多少种不同的号码?
课堂探究
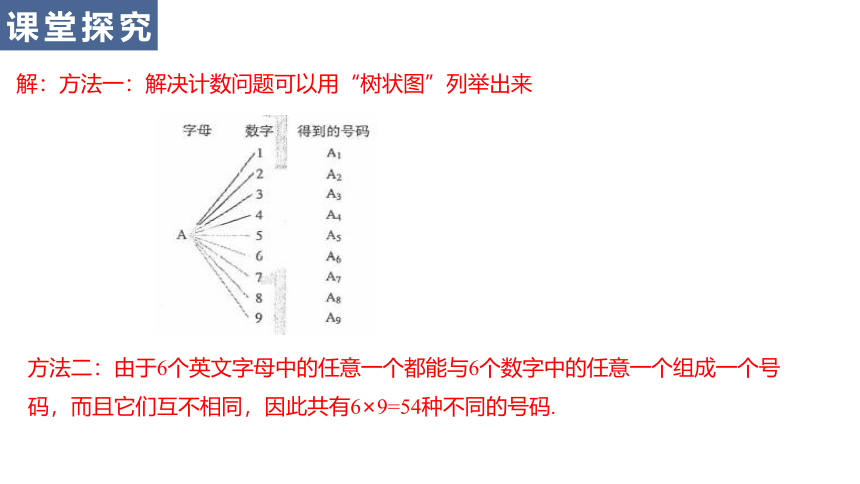
方法二:由于6个英文字母中的任意一个都能与6个数字中的任意一个组成一个号码,而且它们互不相同,因此共有6×9=54种不同的号码.
解:方法一:解决计数问题可以用“树状图”列举出来
课堂探究
完成一件事需要两个步骤,做第1步有m种不同的方法,
做第2步有 n 种不同的方法,那么完成这件事共有多少
种不同的方法?
这个叫做分步乘法计数原理
思考:有n个不同步骤了?
课堂探究
例1 某班有男生30名、女生24名,从中任选1名男生或1名女
生代表班级参加比赛,共有多少种不同的选法?
30+24=54
例题解析
例2 某班有男生30名、女生24名,从中任选男生和女生
各1名代表班级参加比赛,共有多少种不同的选法?
解: .
例题解析
两个原理的区别与联系:
分类加法计数原理 分步乘法计数原理
关键词 分类 分步
区别 每类方法都能独立完成这件事 各步都完成,才能完成这件事
各类方法之间是互斥的、并列的、独立的 各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复
联系 都是用来解决关于完成一件事的不同方法种数的问题 例题解析
其中,序号的编码规则为:
(1)由10个阿拉伯数字和除O,I之外的24个
英文字母组成;
(2)最多只能有2个英文字母.
如果某地级市发牌机关采用5位序号编码,那么这个发牌机关最多能发放多少张汽车号牌?
例3 通常,我国民用汽车号牌的编号由两部分组成:第一部分为用汉字表示的省、自治区、直辖市简称和用英文字母表示的发牌机关代号,第二部分为由阿拉伯数字和英文字母组成的序号,如图所示.
例题解析
例题解析
解:由号牌编号的组成可知,这个发牌机关所能发放的最多号牌数就是序号的个数.根据序号编码规则,5位序号可以分为三类:没有字母,有1个字母,有2个字母.
(1)当没有字母时,序号的每一位都是数字.确定一个序号可以分5个步骤,每一步都可以从10个数字中选1个,各有10种选法.根据分步乘法计数原理,这类号牌张数为.
(2)当有1个字母时,这个字母可以分别在序号的第1位、第2位、第3位、第4位或第5位,这类序号可以分为五个子类.
当第1位是字母时,分5个步骤确定一个序号中的字母和数字:第1步,从24个字母中选1个放在第1位,有24种选法;第2~5步都是从10个数字中选1个放在相应的位置,各有10种选法.根据分步乘法计数原理,号牌张数为.
同样,其余四个子类号牌也各有240000张.
根据分类加法计数原理,这类号牌张数一共为
例题解析
(3)当有2个字母时,根据这2个字母在序号中的位置,可以将这类序号分为十个子类:第1位和第2位,第1位和第3位,第1位和第4位,第1位和第5位,第2位和第3位,第2位和第4位,第2位和第5位,第3位和第4位,第3位和第5位,第4位和第5位.
当第1位和第2位是字母时,分5个步骤确定一个序号中的字母和数字:第1,2步都是从24个字母中选1个分别放在第1位、第2位,各有24种选法;第3~5步都是从10个数字中选1个放在相应的位置,各有10种选法.根据分步乘法计数原理,号牌张数为
.
于是,这类号牌张数一共为.
综合(1)(2)(3),号牌张数为
100000+1200000+5760000=7060000.
例题解析
练习1.
(1)在分类加法计数原理中,两类不同方案中的方法可以相同.( ) (2)在分类加法计数原理中,每类方案中的方法都能完成这件事. ( )
(3)在分步乘法计数原理中,每个步骤中完成这个步骤的方法是各不相同的. ( )
(4)在分步乘法计数原理中,事情是分两步完成的,其中任何一个单独的步骤都能完成这件事. ( )
练习巩固
练习2:某商场共有4个门,购物者若从任意一个门进,从任意一个门出,求不同走法的种数.
16
练习巩固
练习3:某外语组有9人,每人至少会英语和日语中的一门,其中7人会英
语,3人会日语,从中选出会英语和日语的各一人到边远地区支教,有多少
种不同的选法
练习巩固
解答:设既会英语又会日语的人为甲,则甲有入选和不入选两类情形,入选后又分两种情况:(1)教英语;(2)教日语.
第一类:甲入选.
(1)甲教英语,再从只会日语的2人中选1人,由分步乘法计数原理,有1×2=2(种)选法;
(2)甲教日语,再从只会英语的6人中选1人,由分步乘法计数原理,有1×6=6(种)选法.故甲入选的不同选法共有2+6=8(种).
第二类:甲不入选.
可分两步:第一步,从只会英语的6人中选1人有6种选法;第二步,从只会日语的2人中选1人有2种选法.由分步乘法计数原理,有6×2=12(种)不同的选法.综上,共有8+12=20(种)不同的选法.
练习巩固
练习巩固
你收获了什么?
第六章 记数原理
6.1 分类加法计数原理与分步乘法计数原理
新课引入
问题1 用一个大写的英文字母或一个阿拉伯数字给教室
里的一个座位编号,总共能编出多少种不同的号码?
新课引入
问题2 用一个大写的英文字母和一个阿拉伯数字给教室
里的一个座位编号,总共能编出多少种不同的号码?
课堂探究
问题1 用一个大写的英文字母或一个阿拉伯数字给教室
里的一个座位编号,总共能编出多少种不同的号码?
问题2 用一个大写的英文字母和一个阿拉伯数字给教室
里的一个座位编号,总共能编出多少种不同的号码?
36种
260种
这两个问题有什么区别?
完成一件事有两类不同方案,在第1类方案中有m种不同的
方法,在第2类方案中有n种不同的方法,那么完成这件事
共有多少种不同的方法?
这个叫分类加法计数原理
思考:有n类不同方案了?
课堂探究
用前6个大写的英文字母和1~9个阿拉伯数字,以A1, A2,…A9,B1,B2,…的方式给教室里的一个座位编号,总共能编出多少种不同的号码?
课堂探究
方法二:由于6个英文字母中的任意一个都能与6个数字中的任意一个组成一个号码,而且它们互不相同,因此共有6×9=54种不同的号码.
解:方法一:解决计数问题可以用“树状图”列举出来
课堂探究
完成一件事需要两个步骤,做第1步有m种不同的方法,
做第2步有 n 种不同的方法,那么完成这件事共有多少
种不同的方法?
这个叫做分步乘法计数原理
思考:有n个不同步骤了?
课堂探究
例1 某班有男生30名、女生24名,从中任选1名男生或1名女
生代表班级参加比赛,共有多少种不同的选法?
30+24=54
例题解析
例2 某班有男生30名、女生24名,从中任选男生和女生
各1名代表班级参加比赛,共有多少种不同的选法?
解: .
例题解析
两个原理的区别与联系:
分类加法计数原理 分步乘法计数原理
关键词 分类 分步
区别 每类方法都能独立完成这件事 各步都完成,才能完成这件事
各类方法之间是互斥的、并列的、独立的 各步之间是关联的、独立的,“关联”确保不遗漏,“独立”确保不重复
联系 都是用来解决关于完成一件事的不同方法种数的问题 例题解析
其中,序号的编码规则为:
(1)由10个阿拉伯数字和除O,I之外的24个
英文字母组成;
(2)最多只能有2个英文字母.
如果某地级市发牌机关采用5位序号编码,那么这个发牌机关最多能发放多少张汽车号牌?
例3 通常,我国民用汽车号牌的编号由两部分组成:第一部分为用汉字表示的省、自治区、直辖市简称和用英文字母表示的发牌机关代号,第二部分为由阿拉伯数字和英文字母组成的序号,如图所示.
例题解析
例题解析
解:由号牌编号的组成可知,这个发牌机关所能发放的最多号牌数就是序号的个数.根据序号编码规则,5位序号可以分为三类:没有字母,有1个字母,有2个字母.
(1)当没有字母时,序号的每一位都是数字.确定一个序号可以分5个步骤,每一步都可以从10个数字中选1个,各有10种选法.根据分步乘法计数原理,这类号牌张数为.
(2)当有1个字母时,这个字母可以分别在序号的第1位、第2位、第3位、第4位或第5位,这类序号可以分为五个子类.
当第1位是字母时,分5个步骤确定一个序号中的字母和数字:第1步,从24个字母中选1个放在第1位,有24种选法;第2~5步都是从10个数字中选1个放在相应的位置,各有10种选法.根据分步乘法计数原理,号牌张数为.
同样,其余四个子类号牌也各有240000张.
根据分类加法计数原理,这类号牌张数一共为
例题解析
(3)当有2个字母时,根据这2个字母在序号中的位置,可以将这类序号分为十个子类:第1位和第2位,第1位和第3位,第1位和第4位,第1位和第5位,第2位和第3位,第2位和第4位,第2位和第5位,第3位和第4位,第3位和第5位,第4位和第5位.
当第1位和第2位是字母时,分5个步骤确定一个序号中的字母和数字:第1,2步都是从24个字母中选1个分别放在第1位、第2位,各有24种选法;第3~5步都是从10个数字中选1个放在相应的位置,各有10种选法.根据分步乘法计数原理,号牌张数为
.
于是,这类号牌张数一共为.
综合(1)(2)(3),号牌张数为
100000+1200000+5760000=7060000.
例题解析
练习1.
(1)在分类加法计数原理中,两类不同方案中的方法可以相同.( ) (2)在分类加法计数原理中,每类方案中的方法都能完成这件事. ( )
(3)在分步乘法计数原理中,每个步骤中完成这个步骤的方法是各不相同的. ( )
(4)在分步乘法计数原理中,事情是分两步完成的,其中任何一个单独的步骤都能完成这件事. ( )
练习巩固
练习2:某商场共有4个门,购物者若从任意一个门进,从任意一个门出,求不同走法的种数.
16
练习巩固
练习3:某外语组有9人,每人至少会英语和日语中的一门,其中7人会英
语,3人会日语,从中选出会英语和日语的各一人到边远地区支教,有多少
种不同的选法
练习巩固
解答:设既会英语又会日语的人为甲,则甲有入选和不入选两类情形,入选后又分两种情况:(1)教英语;(2)教日语.
第一类:甲入选.
(1)甲教英语,再从只会日语的2人中选1人,由分步乘法计数原理,有1×2=2(种)选法;
(2)甲教日语,再从只会英语的6人中选1人,由分步乘法计数原理,有1×6=6(种)选法.故甲入选的不同选法共有2+6=8(种).
第二类:甲不入选.
可分两步:第一步,从只会英语的6人中选1人有6种选法;第二步,从只会日语的2人中选1人有2种选法.由分步乘法计数原理,有6×2=12(种)不同的选法.综上,共有8+12=20(种)不同的选法.
练习巩固
练习巩固
你收获了什么?
