鲁教版(五四制)数学七年级上册 1.2 图形的全等 教案
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 1.2 图形的全等 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 94.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 09:50:24 | ||
图片预览


文档简介
图形的全等
【教学目标】
1.理解图形全等的概念和特征,并能识别图形的全等。
2.掌握全等三角形对应边相等、对应角相等的性质,并能利用全等三角形的特征解决一些实际问题。
3.尝试从不同角度寻求解决问题的方法,并在解决问题的过程中提高对图形的分析能力。
4.掌握全等三角形对应边相等,对应角相等的性质,并能进行简单的推理和计算,解决一些实际问题。
5.联系学生的生活环境,创设情景,使学生通过观察、操作、交流和反思,获得必需的数学知识,激发学生的学习兴趣,充分体验全等图形是有效描述现实世界的重要手段。
【教学重难点】
正确识别全等三角形的对应元素。
【教学过程】
(一)活动一:情境创设(全体活动)。
1.展示图片(见图1)。
图1
2.讨论问题:图中有多少条鱼?这些鱼之间有什么关系?
3.全班交流。
4.明晰:
(1)图中共有16条小鱼;
(2)这些小鱼是能够完全重合的图形;
(3)两个能够重合的图形称为全等图形。
5.举出生活中全等图形的例子。
(二)活动二:探究
1.提出问题:
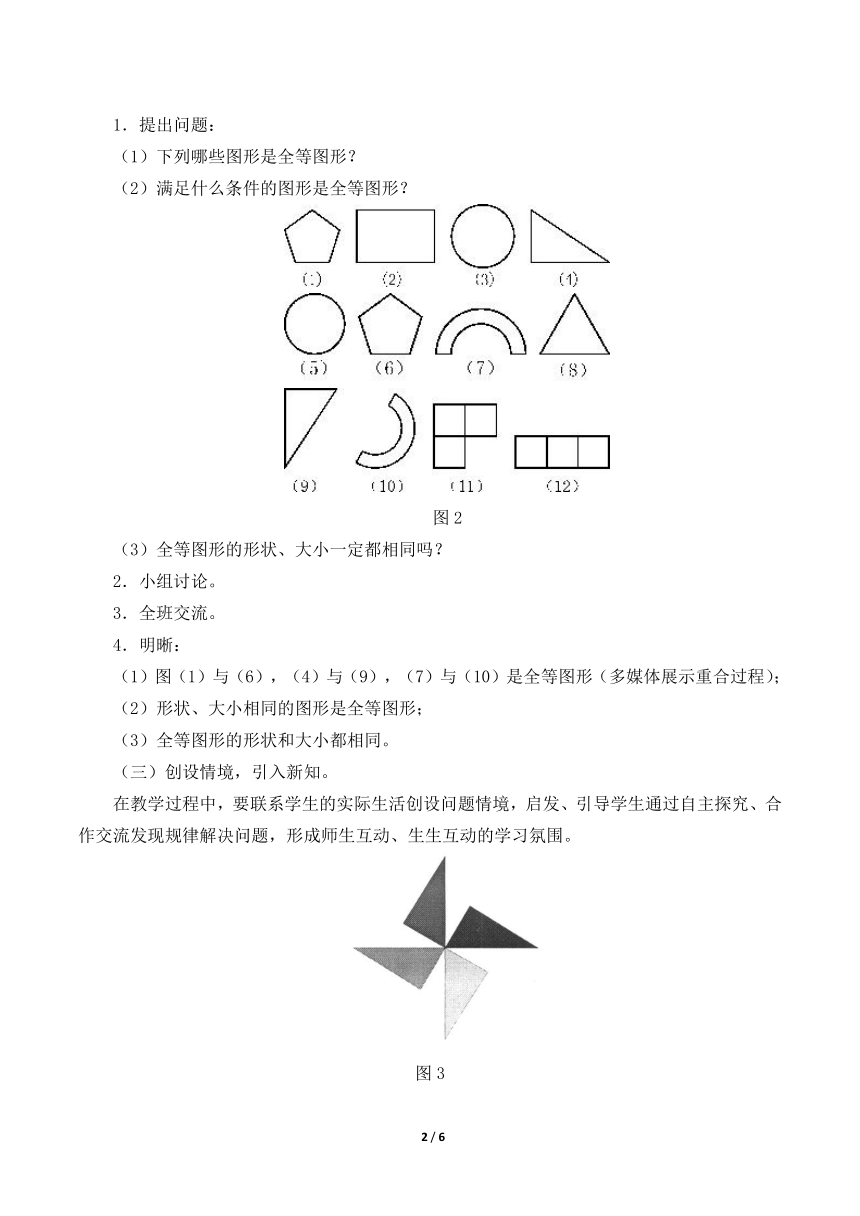
(1)下列哪些图形是全等图形?
(2)满足什么条件的图形是全等图形?
图2
(3)全等图形的形状、大小一定都相同吗?
2.小组讨论。
3.全班交流。
4.明晰:
(1)图(1)与(6),(4)与(9),(7)与(10)是全等图形(多媒体展示重合过程);
(2)形状、大小相同的图形是全等图形;
(3)全等图形的形状和大小都相同。
(三)创设情境,引入新知。
在教学过程中,要联系学生的实际生活创设问题情境,启发、引导学生通过自主探究、合作交流发现规律解决问题,形成师生互动、生生互动的学习氛围。
图3
(电脑展示用“几何画板”制作的旋转的大风车。)
师:同学们,你们都见过大风车吧!“大风车转起来,各地的朋友来相会。”现在请你们仔细地观察这个大风车,看看它是由哪些图形组成的?这些图形有什么特点?
生:它是由四个三角形组成的,这四个三角形是全等的。
师:同学们观察得非常好!在生活中,我们可以发现很多图案都是由全等的三角形组成的。
图4
我们接着一起来研究全等三角形。
(四)新知讲解。
1.通过观察引出全等三角形的有关概念。
师:全等三角形是全等图形的一种,哪些同学能仿照全等图形的概念说一说什么是全等三角形?
生:能够完全重合的两个三角形是全等三角形。
师:很好,看图:
图5
△ABC与△DEF能够重合(用电脑演示重合的过程),那么△ABC与△DEF就是全等三角形。我们可以发现:点A与点D重合,点C与点F重合。我们把这样相互重合的一对点就叫做对应顶点;AB边与DE边重合,这样相互重合的边叫做对应边,∠A与∠D重合,那么它们就是对应角了。
你还能找出其他的对应顶点、对应边、对应角吗?
生:点B与点E是对应点,BC边与EF边是对应边,AC边与DF边也是对应边,∠B与∠E是对应角,∠C与∠F也是对应角。
师:同学们找得很正确。我们知道,两条直线平行、垂直都可以用符号来表示,那么全等三角形用什么来表示呢?
图6
如图,△ABC与△DEF全等,即这两个三角形能够完全重合。我们把它记作:△ABC≌△DEF。读作“△ABC全等于△DEF”。
大家注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。如图,点A与点D.点B与点E、点C与点F是对应点,记作:△ABC≌△DEF。
2.想一想。
全等三角形的对应边、对应角之间有什么样的关系?
(播放两个三角形重合的过程。)
生:全等三角形的对应边相等,对应角相等。
师:好的,这就是全等三角形的性质。
图7
如图,若△ABC≌△EFD,则∠A=∠E,∠B=∠F,∠C=∠D;AB=EF,AC=ED,BC=FD.
3.练一练(电脑展示图形)。
图8
(1)在图8(1)中,△ABC≌△DCB,则AB=( ),AC=( ),BC=( )。
(2)在图8(2)中,△ABC≌△DEC,则∠A=( ),∠B=( ),∠ACB=( )。
(3)在图8(3)中,△ABC≌△AED,则∠BAC=( ),∠B=( ),∠ADE=( )。
生:在图8(1)中,AB=CD,AC=DB,BC=CB.
在图8(2)中,∠A=∠D,∠B=∠E,∠ACB=∠ECD.
在图8(3)中,∠BAC=∠EAD,∠B=∠E,∠ADE=∠ACB.
师:仔细观察图8中的3幅图,两个全等三角形边与边、角与角之间有什么特殊的位置关系?
生:图8(1)中,两个全等三角形有一条边是重合的(即有一条公共边);图8(2)中,两个全等三角形有一个角是对顶角;图8(3)中,全等的两个三角形有一个角是重合的(即有一个公共角)。
师:经过上面的练习,我们知道这些重合的边(或角)就是对应边(或角)。因此我们就可以得到:在全等三角形中,公共边往往是对应边;公共角往往是对应角;对顶角往往是对应角。
师:下面我们继续观察、归纳并总结规律。
图9
(1)在图9(1)中,△ABC≌△DEF,则AB=( ),∠C=( )。
(2)在图9(2)中,△ABC≌△ADE,则AC=( ),∠ABC=( )。
(3)在图9(3)中,△ABC≌△EFD,则BC=( ),∠A=( )。
(4)在图9(4)中,△ABC≌△CDA,则AB=( ),BC=( ),∠B=( )。
生:(1)AB=DE,∠C=∠F;
(2)AC=AE,∠ABC=∠ADE;
(3)BC=DF,∠A=∠E;
(4)AB=DC,BC=AD,∠B=∠D.
师:现在以小组为单位讨论:由上面的(1)(2)(3)可以得到什么规律?由(4)呢?
生:由(1)(2)(3)可知:全等三角形对应边所对的角是对应角,对应角所对的边是对应边;由(4)可知:全等三角形两条对应边所夹的角是对应角。
师:同学们总结得非常好,有了这些规律,我们就更容易找出全等三角形的对应边与对应角了。
下面我们通过练习进一步掌握全等三角形的性质。
例:如图,△ABC≌△BAD,说出它们的对应边和对应角。
解:AC与BD,BC与AD,AB与BA是对应边。
∠ABC与∠BAD,∠BAC与∠ABD,∠C与∠D是对应角。
(五)活动三:设计图案(个体活动,小组活动,全体活动)。
1.自由创意:用多功能尺子在准备好的白纸上设计一幅有趣的或美丽的图案。
要求:
(1)指出图中的全等图形;(2)用水彩笔上色;(3)用简洁的话概括设计意图。(设计过程中伴有轻音乐。)
2.各小组展示并进行评价,推选出本组的佳作。
3.各组推选出的佳作在全班展示,进行评价。
4.教师伴随背景音乐和一幅幅美丽的全等图片,用几句有关全等的语言说明全等在日常生活中的广泛运用。
(六)小结。
师:通过本节课的学习,你有什么收获?
6 / 6
【教学目标】
1.理解图形全等的概念和特征,并能识别图形的全等。
2.掌握全等三角形对应边相等、对应角相等的性质,并能利用全等三角形的特征解决一些实际问题。
3.尝试从不同角度寻求解决问题的方法,并在解决问题的过程中提高对图形的分析能力。
4.掌握全等三角形对应边相等,对应角相等的性质,并能进行简单的推理和计算,解决一些实际问题。
5.联系学生的生活环境,创设情景,使学生通过观察、操作、交流和反思,获得必需的数学知识,激发学生的学习兴趣,充分体验全等图形是有效描述现实世界的重要手段。
【教学重难点】
正确识别全等三角形的对应元素。
【教学过程】
(一)活动一:情境创设(全体活动)。
1.展示图片(见图1)。
图1
2.讨论问题:图中有多少条鱼?这些鱼之间有什么关系?
3.全班交流。
4.明晰:
(1)图中共有16条小鱼;
(2)这些小鱼是能够完全重合的图形;
(3)两个能够重合的图形称为全等图形。
5.举出生活中全等图形的例子。
(二)活动二:探究
1.提出问题:
(1)下列哪些图形是全等图形?
(2)满足什么条件的图形是全等图形?
图2
(3)全等图形的形状、大小一定都相同吗?
2.小组讨论。
3.全班交流。
4.明晰:
(1)图(1)与(6),(4)与(9),(7)与(10)是全等图形(多媒体展示重合过程);
(2)形状、大小相同的图形是全等图形;
(3)全等图形的形状和大小都相同。
(三)创设情境,引入新知。
在教学过程中,要联系学生的实际生活创设问题情境,启发、引导学生通过自主探究、合作交流发现规律解决问题,形成师生互动、生生互动的学习氛围。
图3
(电脑展示用“几何画板”制作的旋转的大风车。)
师:同学们,你们都见过大风车吧!“大风车转起来,各地的朋友来相会。”现在请你们仔细地观察这个大风车,看看它是由哪些图形组成的?这些图形有什么特点?
生:它是由四个三角形组成的,这四个三角形是全等的。
师:同学们观察得非常好!在生活中,我们可以发现很多图案都是由全等的三角形组成的。
图4
我们接着一起来研究全等三角形。
(四)新知讲解。
1.通过观察引出全等三角形的有关概念。
师:全等三角形是全等图形的一种,哪些同学能仿照全等图形的概念说一说什么是全等三角形?
生:能够完全重合的两个三角形是全等三角形。
师:很好,看图:
图5
△ABC与△DEF能够重合(用电脑演示重合的过程),那么△ABC与△DEF就是全等三角形。我们可以发现:点A与点D重合,点C与点F重合。我们把这样相互重合的一对点就叫做对应顶点;AB边与DE边重合,这样相互重合的边叫做对应边,∠A与∠D重合,那么它们就是对应角了。
你还能找出其他的对应顶点、对应边、对应角吗?
生:点B与点E是对应点,BC边与EF边是对应边,AC边与DF边也是对应边,∠B与∠E是对应角,∠C与∠F也是对应角。
师:同学们找得很正确。我们知道,两条直线平行、垂直都可以用符号来表示,那么全等三角形用什么来表示呢?
图6
如图,△ABC与△DEF全等,即这两个三角形能够完全重合。我们把它记作:△ABC≌△DEF。读作“△ABC全等于△DEF”。
大家注意:记两个三角形全等时,通常把表示对应顶点的字母写在对应的位置上。如图,点A与点D.点B与点E、点C与点F是对应点,记作:△ABC≌△DEF。
2.想一想。
全等三角形的对应边、对应角之间有什么样的关系?
(播放两个三角形重合的过程。)
生:全等三角形的对应边相等,对应角相等。
师:好的,这就是全等三角形的性质。
图7
如图,若△ABC≌△EFD,则∠A=∠E,∠B=∠F,∠C=∠D;AB=EF,AC=ED,BC=FD.
3.练一练(电脑展示图形)。
图8
(1)在图8(1)中,△ABC≌△DCB,则AB=( ),AC=( ),BC=( )。
(2)在图8(2)中,△ABC≌△DEC,则∠A=( ),∠B=( ),∠ACB=( )。
(3)在图8(3)中,△ABC≌△AED,则∠BAC=( ),∠B=( ),∠ADE=( )。
生:在图8(1)中,AB=CD,AC=DB,BC=CB.
在图8(2)中,∠A=∠D,∠B=∠E,∠ACB=∠ECD.
在图8(3)中,∠BAC=∠EAD,∠B=∠E,∠ADE=∠ACB.
师:仔细观察图8中的3幅图,两个全等三角形边与边、角与角之间有什么特殊的位置关系?
生:图8(1)中,两个全等三角形有一条边是重合的(即有一条公共边);图8(2)中,两个全等三角形有一个角是对顶角;图8(3)中,全等的两个三角形有一个角是重合的(即有一个公共角)。
师:经过上面的练习,我们知道这些重合的边(或角)就是对应边(或角)。因此我们就可以得到:在全等三角形中,公共边往往是对应边;公共角往往是对应角;对顶角往往是对应角。
师:下面我们继续观察、归纳并总结规律。
图9
(1)在图9(1)中,△ABC≌△DEF,则AB=( ),∠C=( )。
(2)在图9(2)中,△ABC≌△ADE,则AC=( ),∠ABC=( )。
(3)在图9(3)中,△ABC≌△EFD,则BC=( ),∠A=( )。
(4)在图9(4)中,△ABC≌△CDA,则AB=( ),BC=( ),∠B=( )。
生:(1)AB=DE,∠C=∠F;
(2)AC=AE,∠ABC=∠ADE;
(3)BC=DF,∠A=∠E;
(4)AB=DC,BC=AD,∠B=∠D.
师:现在以小组为单位讨论:由上面的(1)(2)(3)可以得到什么规律?由(4)呢?
生:由(1)(2)(3)可知:全等三角形对应边所对的角是对应角,对应角所对的边是对应边;由(4)可知:全等三角形两条对应边所夹的角是对应角。
师:同学们总结得非常好,有了这些规律,我们就更容易找出全等三角形的对应边与对应角了。
下面我们通过练习进一步掌握全等三角形的性质。
例:如图,△ABC≌△BAD,说出它们的对应边和对应角。
解:AC与BD,BC与AD,AB与BA是对应边。
∠ABC与∠BAD,∠BAC与∠ABD,∠C与∠D是对应角。
(五)活动三:设计图案(个体活动,小组活动,全体活动)。
1.自由创意:用多功能尺子在准备好的白纸上设计一幅有趣的或美丽的图案。
要求:
(1)指出图中的全等图形;(2)用水彩笔上色;(3)用简洁的话概括设计意图。(设计过程中伴有轻音乐。)
2.各小组展示并进行评价,推选出本组的佳作。
3.各组推选出的佳作在全班展示,进行评价。
4.教师伴随背景音乐和一幅幅美丽的全等图片,用几句有关全等的语言说明全等在日常生活中的广泛运用。
(六)小结。
师:通过本节课的学习,你有什么收获?
6 / 6
