小学数学西师大版四年级下2.6 乘除法的关系和乘法运算律 解决问题课件(共30张PPT)
文档属性
| 名称 | 小学数学西师大版四年级下2.6 乘除法的关系和乘法运算律 解决问题课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 00:00:00 | ||
图片预览






文档简介
(共30张PPT)
西师版数学四年级(下)
第6课时 解决问题(1)
乘除法的关系和乘法运算律
二
1. 尝试运用所学知识解决实际问题,培养运用所学知识解决实际问题的能力。
2. 在与他人合作、交流的基础上,会进行反思和总结,并形成解决具有问题特征的数学问题的基本策略,同时体会解决问题策略的多样性。
3. 在解决问题的过程中,获得问题解决的积极情感体验,培养发散思维。
学习目标
【重点】
掌握相遇问题的基本特征及数量关系,能应用所
学知识解决实际问题。
【难点】
利用多种策略解决实际问题,培养画
线段图分析数量关系的能力。
课堂导入
余刚每分钟走75米,他从家走到少年宫要5分钟,余刚家离少年宫有多少米?
路程 = 速度×时间
75×5
= 375(米)
答:余刚家离少年宫有375米。
探究新知
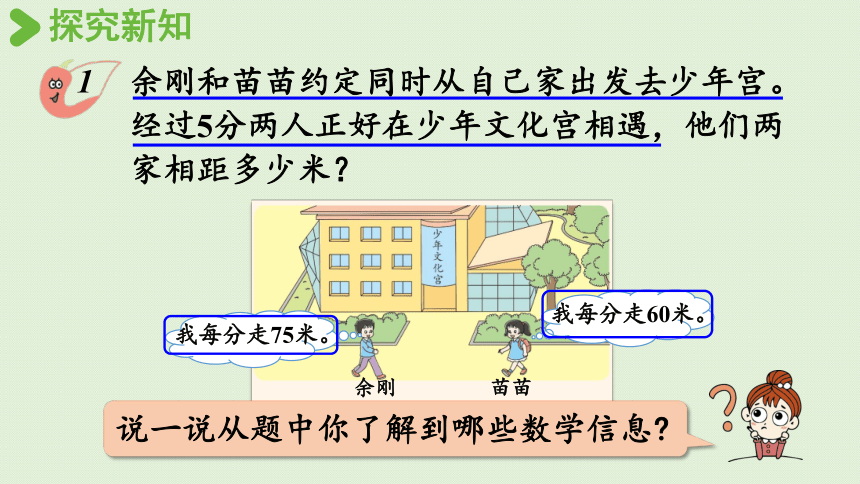
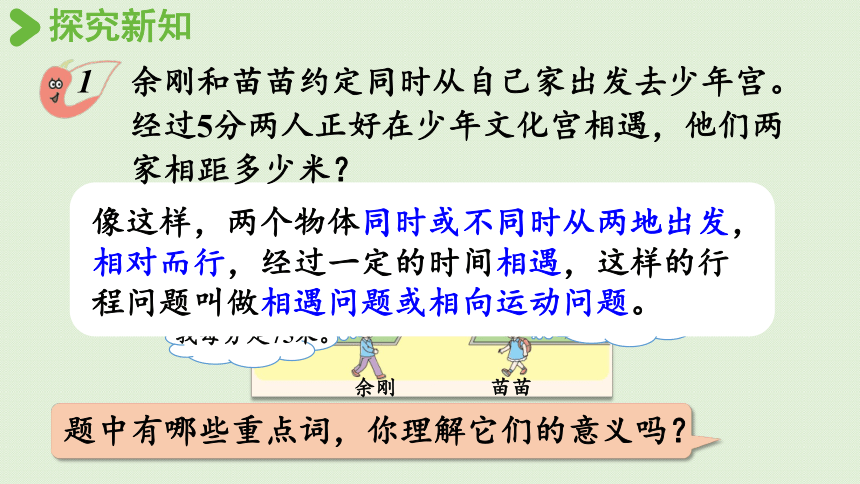
余刚和苗苗约定同时从自己家出发去少年宫。经过5分两人正好在少年文化宫相遇,他们两家相距多少米?
说一说从题中你了解到哪些数学信息
我每分走60米。
我每分走75米。
余刚
苗苗
1
探究新知
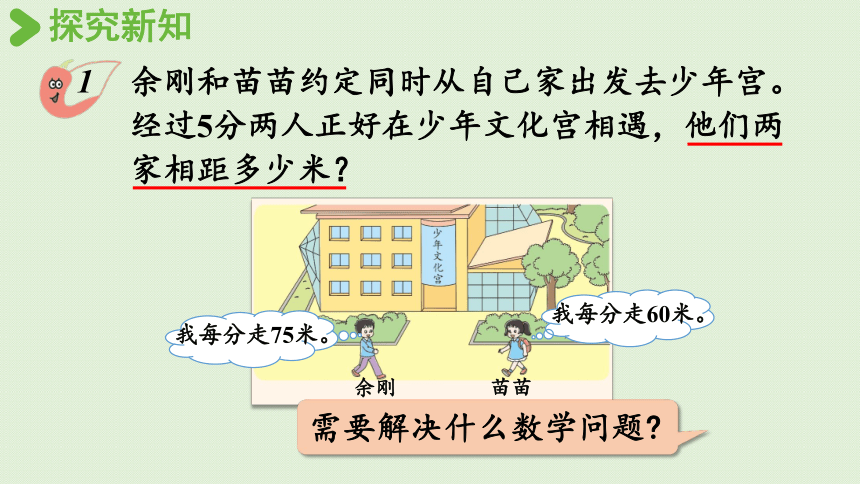
余刚和苗苗约定同时从自己家出发去少年宫。经过5分两人正好在少年文化宫相遇,他们两家相距多少米?
我每分走60米。
我每分走75米。
余刚
苗苗
需要解决什么数学问题
1
探究新知
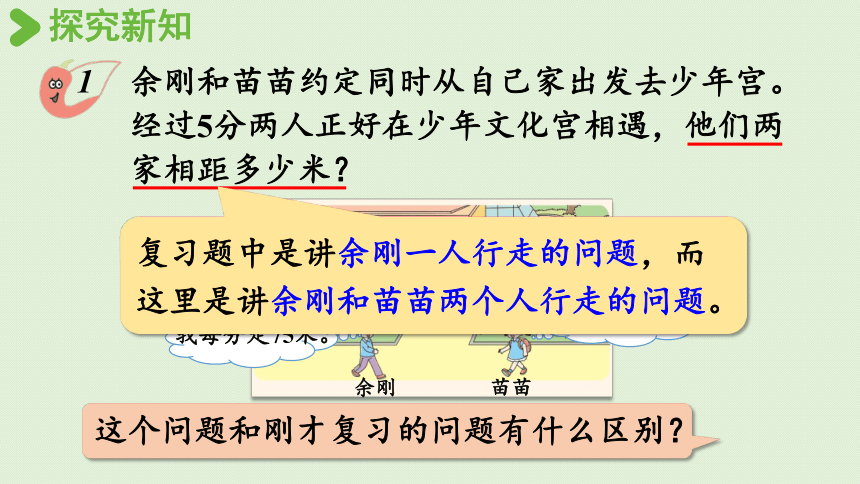
余刚和苗苗约定同时从自己家出发去少年宫。经过5分两人正好在少年文化宫相遇,他们两家相距多少米?
这个问题和刚才复习的问题有什么区别?
我每分走60米。
我每分走75米。
余刚
苗苗
复习题中是讲余刚一人行走的问题,而这里是讲余刚和苗苗两个人行走的问题。
1
探究新知
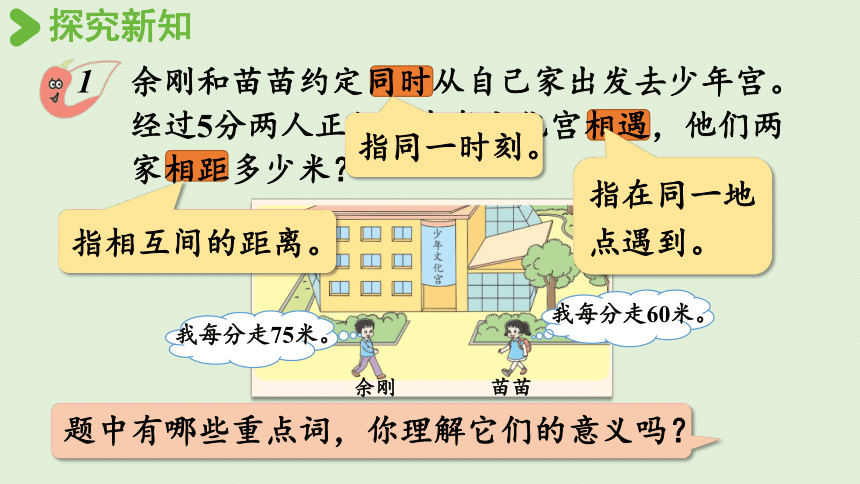
余刚和苗苗约定同时从自己家出发去少年宫。经过5分两人正好在少年文化宫相遇,他们两家相距多少米?
我每分走60米。
我每分走75米。
余刚
苗苗
指在同一地点遇到。
1
指同一时刻。
指相互间的距离。
题中有哪些重点词,你理解它们的意义吗?
探究新知
我每分走60米。
我每分走75米。
余刚
苗苗
1
题中有哪些重点词,你理解它们的意义吗?
像这样,两个物体同时或不同时从两地出发,相对而行,经过一定的时间相遇,这样的行程问题叫做相遇问题或相向运动问题。
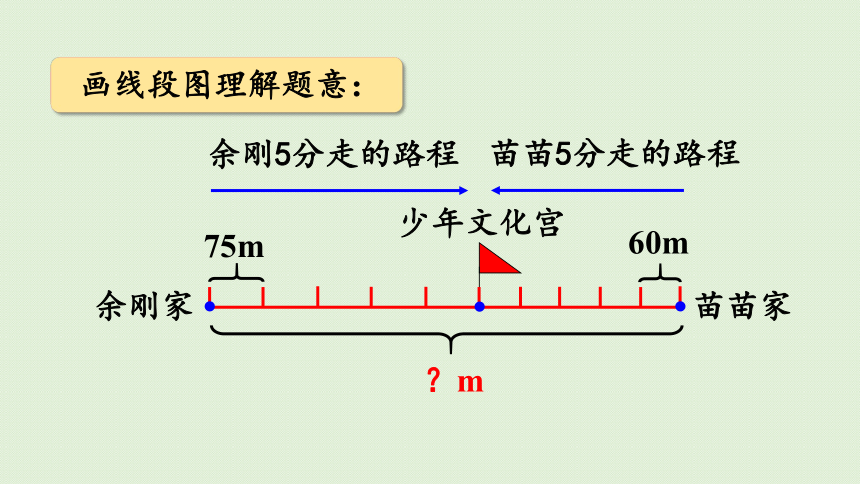
余刚和苗苗约定同时从自己家出发去少年宫。经过5分两人正好在少年文化宫相遇,他们两家相距多少米?
苗苗家
余刚家
少年文化宫
75m
余刚5分走的路程
60m
苗苗5分走的路程
?m
画线段图理解题意:
75 × 5 + 60× 5
先算余刚5分走的路程。
再算苗苗5分走的路程。
1
两家相距的路程,正好是他俩5分所走的路程和。
你能列出综合算式并说出理由吗
75 × 5 + 60× 5
= 375 + 300
= 675(米)
1
你能列出综合算式并说出理由吗
你能列出综合算式并说出理由吗
( 75 + 60 ) ×5
再乘5,算出余刚和苗苗5分共走的路程,也就是两家相距的路程。
先算余刚和苗苗每分共走的路程。
2
你能列出综合算式并说出理由吗
( 75 + 60 ) ×5
= 135×5
= 675(米)
2
答:他们两家相距675米。
( 75 + 60 ) ×5
= 135×5
= 675(米)
你能列出综合算式并说出理由吗
时间
2
路程
两人的速度和。
路程 = 速度(和) × 时间
75×5 + 60×5
= 375 + 300
= 675(米)
1
( 75 + 60 ) ×5
= 135×5
= 675(米)
2
仔细观察这两种解法,你有什么发现
75×5 + 60×5
( 75 + 60 ) ×5
=
乘法分配律
75×5 + 60×5
= 375 + 300
= 675(米)
1
( 75 + 60 ) ×5
= 135×5
= 675(米)
2
你更喜欢用哪种解决方法 为什么?
路程 = 速度(和) × 时间
甲、乙两辆汽车同时从车站出发,向相反的方向行驶,甲车每时行45km,乙车每时行52km,两车开出3时后相距多少千米?
这两辆车是怎样行驶的
向相反
你能画线段图分析吗?
试一试
这道题和例题1有什么相同点和不同点?
相同点:
两道题都是两个物体同时出发做运动。
最后都是求两个物体行走的路程之和。
不同点:
例题1是从两地出发相向而行。
而这道题是从同一点地出发向相反的方向行驶。
甲、乙两辆汽车同时从车站出发,向相反的方向行驶,甲车每时行45km,乙车每时行52km,两车开出3时后相距多少千米?
甲
车站
45km
乙
52km
?km
你能画线段图分析吗?
试一试
( 45 + 52 ) ×3
= 97×3
= 291(千米)
答:两车开出3时后相距291千米。
45×3 + 52×3
= 135 + 156
= 291(千米)
1
2
想一想刚才解决的两道行程问题,它们有什么特点?解题时用到了怎样的数量关系?
两道题都是两个物体同时运动。
要求他们行走的总路程,可以先算出两个物体分别行的路程,然后再相加。
也可以用“路程 = 速度(和) × 时间”来解决。
课堂练习
1. 王刚和丽丽分别从自己家出发去看电影。王刚
骑摩托车,每分行600m,丽丽骑自行车,每分
行200m。丽丽比王刚提前2分出发,再经过7分
后他们同时到达电影院。
从“丽丽比王刚提前2分出发”可以想到什么?
根据以上信息,提出一个数学问题,并交流解决方法。
王刚和丽丽同时行了7分。
丽丽从家到电影院一共行了(2+7)分。
(教材第21页课堂活动第1题)
王刚和丽丽一共行驶了多少米?
200×2
( 600+200) ×7
+
丽丽提前出发2分行的路程。
王刚和丽丽同时行7分,两人7分行驶的路程。
两人所走的路程和,也就是两人一共行驶的路程。
(教材第21页课堂活动第1题)
王刚和丽丽一共行驶了多少米?
200×2
( 600+200) ×7
+
= 400 + 5600
= 6000(米)
答:王刚和丽丽一共行驶了6000米。
(教材第21页课堂活动第1题)
2. 上海到武汉的长江航线长多少千米?
( 26 + 17 ) ×25
答:上海到武汉的长江航线长1075千米。
= 43×25
= 1075 (千米)
两船同时相对开出,经过25时相遇。
26千米/时
17千米/时
武汉
上海
(教材第22页练习六第1题)
王丽家在学校的东面,何川家在学校的西面,两人同时离开学校回家,王丽每分行70m,何川每分行80m,经过12分两人同时到家。他们两家相距多少米 ?
(教材第22页练习六第2题)
何川
王丽
王丽家在学校的东面,何川家在学校的西面,两人同时离开学校回家,王丽每分行70m,何川每分行80m,经过12分两人同时到家。他们两家相距多少米 ?
( 70 + 80 ) ×12
= 150×12
= 1800 (米)
答:他们两家相距1800米。
(教材第22页练习六第2题)
课堂小结
相遇
问题
这节课你有什么收获?
解决问题(1)
路程 = 速度(和) × 时间
可以先算出两个物体分别行的路程,然后再相加。
两个物体同时运动
02
01
课后作业
相关练习。
练习六第1、2、8题和思考题。
西师版数学四年级(下)
第6课时 解决问题(1)
乘除法的关系和乘法运算律
二
1. 尝试运用所学知识解决实际问题,培养运用所学知识解决实际问题的能力。
2. 在与他人合作、交流的基础上,会进行反思和总结,并形成解决具有问题特征的数学问题的基本策略,同时体会解决问题策略的多样性。
3. 在解决问题的过程中,获得问题解决的积极情感体验,培养发散思维。
学习目标
【重点】
掌握相遇问题的基本特征及数量关系,能应用所
学知识解决实际问题。
【难点】
利用多种策略解决实际问题,培养画
线段图分析数量关系的能力。
课堂导入
余刚每分钟走75米,他从家走到少年宫要5分钟,余刚家离少年宫有多少米?
路程 = 速度×时间
75×5
= 375(米)
答:余刚家离少年宫有375米。
探究新知
余刚和苗苗约定同时从自己家出发去少年宫。经过5分两人正好在少年文化宫相遇,他们两家相距多少米?
说一说从题中你了解到哪些数学信息
我每分走60米。
我每分走75米。
余刚
苗苗
1
探究新知
余刚和苗苗约定同时从自己家出发去少年宫。经过5分两人正好在少年文化宫相遇,他们两家相距多少米?
我每分走60米。
我每分走75米。
余刚
苗苗
需要解决什么数学问题
1
探究新知
余刚和苗苗约定同时从自己家出发去少年宫。经过5分两人正好在少年文化宫相遇,他们两家相距多少米?
这个问题和刚才复习的问题有什么区别?
我每分走60米。
我每分走75米。
余刚
苗苗
复习题中是讲余刚一人行走的问题,而这里是讲余刚和苗苗两个人行走的问题。
1
探究新知
余刚和苗苗约定同时从自己家出发去少年宫。经过5分两人正好在少年文化宫相遇,他们两家相距多少米?
我每分走60米。
我每分走75米。
余刚
苗苗
指在同一地点遇到。
1
指同一时刻。
指相互间的距离。
题中有哪些重点词,你理解它们的意义吗?
探究新知
我每分走60米。
我每分走75米。
余刚
苗苗
1
题中有哪些重点词,你理解它们的意义吗?
像这样,两个物体同时或不同时从两地出发,相对而行,经过一定的时间相遇,这样的行程问题叫做相遇问题或相向运动问题。
余刚和苗苗约定同时从自己家出发去少年宫。经过5分两人正好在少年文化宫相遇,他们两家相距多少米?
苗苗家
余刚家
少年文化宫
75m
余刚5分走的路程
60m
苗苗5分走的路程
?m
画线段图理解题意:
75 × 5 + 60× 5
先算余刚5分走的路程。
再算苗苗5分走的路程。
1
两家相距的路程,正好是他俩5分所走的路程和。
你能列出综合算式并说出理由吗
75 × 5 + 60× 5
= 375 + 300
= 675(米)
1
你能列出综合算式并说出理由吗
你能列出综合算式并说出理由吗
( 75 + 60 ) ×5
再乘5,算出余刚和苗苗5分共走的路程,也就是两家相距的路程。
先算余刚和苗苗每分共走的路程。
2
你能列出综合算式并说出理由吗
( 75 + 60 ) ×5
= 135×5
= 675(米)
2
答:他们两家相距675米。
( 75 + 60 ) ×5
= 135×5
= 675(米)
你能列出综合算式并说出理由吗
时间
2
路程
两人的速度和。
路程 = 速度(和) × 时间
75×5 + 60×5
= 375 + 300
= 675(米)
1
( 75 + 60 ) ×5
= 135×5
= 675(米)
2
仔细观察这两种解法,你有什么发现
75×5 + 60×5
( 75 + 60 ) ×5
=
乘法分配律
75×5 + 60×5
= 375 + 300
= 675(米)
1
( 75 + 60 ) ×5
= 135×5
= 675(米)
2
你更喜欢用哪种解决方法 为什么?
路程 = 速度(和) × 时间
甲、乙两辆汽车同时从车站出发,向相反的方向行驶,甲车每时行45km,乙车每时行52km,两车开出3时后相距多少千米?
这两辆车是怎样行驶的
向相反
你能画线段图分析吗?
试一试
这道题和例题1有什么相同点和不同点?
相同点:
两道题都是两个物体同时出发做运动。
最后都是求两个物体行走的路程之和。
不同点:
例题1是从两地出发相向而行。
而这道题是从同一点地出发向相反的方向行驶。
甲、乙两辆汽车同时从车站出发,向相反的方向行驶,甲车每时行45km,乙车每时行52km,两车开出3时后相距多少千米?
甲
车站
45km
乙
52km
?km
你能画线段图分析吗?
试一试
( 45 + 52 ) ×3
= 97×3
= 291(千米)
答:两车开出3时后相距291千米。
45×3 + 52×3
= 135 + 156
= 291(千米)
1
2
想一想刚才解决的两道行程问题,它们有什么特点?解题时用到了怎样的数量关系?
两道题都是两个物体同时运动。
要求他们行走的总路程,可以先算出两个物体分别行的路程,然后再相加。
也可以用“路程 = 速度(和) × 时间”来解决。
课堂练习
1. 王刚和丽丽分别从自己家出发去看电影。王刚
骑摩托车,每分行600m,丽丽骑自行车,每分
行200m。丽丽比王刚提前2分出发,再经过7分
后他们同时到达电影院。
从“丽丽比王刚提前2分出发”可以想到什么?
根据以上信息,提出一个数学问题,并交流解决方法。
王刚和丽丽同时行了7分。
丽丽从家到电影院一共行了(2+7)分。
(教材第21页课堂活动第1题)
王刚和丽丽一共行驶了多少米?
200×2
( 600+200) ×7
+
丽丽提前出发2分行的路程。
王刚和丽丽同时行7分,两人7分行驶的路程。
两人所走的路程和,也就是两人一共行驶的路程。
(教材第21页课堂活动第1题)
王刚和丽丽一共行驶了多少米?
200×2
( 600+200) ×7
+
= 400 + 5600
= 6000(米)
答:王刚和丽丽一共行驶了6000米。
(教材第21页课堂活动第1题)
2. 上海到武汉的长江航线长多少千米?
( 26 + 17 ) ×25
答:上海到武汉的长江航线长1075千米。
= 43×25
= 1075 (千米)
两船同时相对开出,经过25时相遇。
26千米/时
17千米/时
武汉
上海
(教材第22页练习六第1题)
王丽家在学校的东面,何川家在学校的西面,两人同时离开学校回家,王丽每分行70m,何川每分行80m,经过12分两人同时到家。他们两家相距多少米 ?
(教材第22页练习六第2题)
何川
王丽
王丽家在学校的东面,何川家在学校的西面,两人同时离开学校回家,王丽每分行70m,何川每分行80m,经过12分两人同时到家。他们两家相距多少米 ?
( 70 + 80 ) ×12
= 150×12
= 1800 (米)
答:他们两家相距1800米。
(教材第22页练习六第2题)
课堂小结
相遇
问题
这节课你有什么收获?
解决问题(1)
路程 = 速度(和) × 时间
可以先算出两个物体分别行的路程,然后再相加。
两个物体同时运动
02
01
课后作业
相关练习。
练习六第1、2、8题和思考题。
