小学数学西师大版四年级下2.7 乘除法的关系和乘法运算律 解决问题 课件(共28张PPT)
文档属性
| 名称 | 小学数学西师大版四年级下2.7 乘除法的关系和乘法运算律 解决问题 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
西师版数学四年级(下)
第7课时 解决问题(2)
乘除法的关系和乘法运算律
二
1. 经历解决数学问题的过程,进一步体会具有相遇问题特征的数学问题(工作效率问题)在实际生活中的应用,培养分析、解决问题的能力。
2. 在与他人合作、交流的基础上,体会解决问题策略的多样性。
3. 在解决问题的过程中,感受成功的体验,激发分析、解决问题的兴趣。
学习目标
【重难点】
能分析数量关系,选择解决问题的策略,分析具
有相遇问题特征的数学问题(工作效率问题)的
数量关系。
【重难点】
运用多种策略解决实际问题。
课堂导入
一辆客车和一辆货车同时从两个城市相对开出,客
车平均速度是每时55km,货车平均速度是每时45km。
两车开出5时后相遇,两个城市相距多少千米?
路程 = 速度(和) × 时间
( 55 + 45 ) ×5
答:两个城市相距500千米。
= 100×5
= 500 (千米)
2. 一辆客车和一辆货车同时从相距500km的两个城市相对开出,客车平均速度是每时55km,货车平均
速度是每时45km。两车开出几时后相遇?
时间 = 路程÷速度(和)
500÷ (55 + 45 )
答:两车开出5时后相遇。
= 500÷100
= 5(时)
探究新知
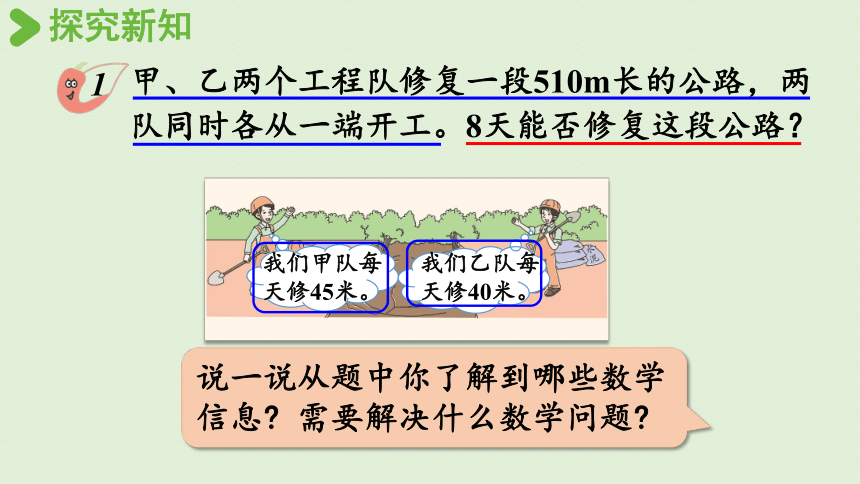
甲、乙两个工程队修复一段510m长的公路,两队同时各从一端开工。8天能否修复这段公路?
说一说从题中你了解到哪些数学信息 需要解决什么数学问题
我们甲队每天修45米。
我们乙队每天修40米。
1
这道题与复习题2对比,你有什么发现
这道题与复习题2很像,复习题2是相遇问题,而这道题是两个工程队修路的工作效率问题。
这两道题都是知道总的路程和两车(队)的速度,求他们的相遇时间(修复完这段公路的时间)。
要求“8天能否修复这段公路”,你的解题思路是怎样的
可以先算出两队合修这段公路需要多少天,再与8天进行比较,进行判断。
也可以先算出两个队8天修复的公路,再与公路总长进行比较,进行判断。
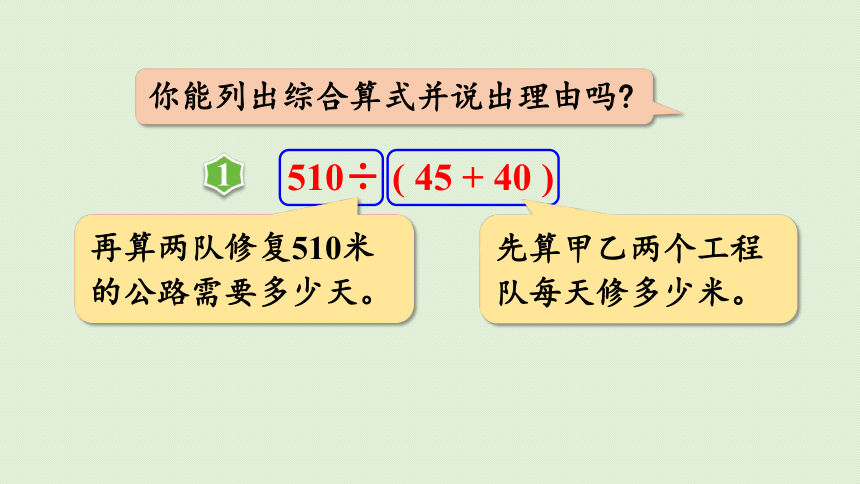
510÷ ( 45 + 40 )
再算两队修复510米的公路需要多少天。
先算甲乙两个工程队每天修多少米。
1
你能列出综合算式并说出理由吗
510÷ ( 45 + 40 )
= 510÷85
= 6 (天)
1
你能列出综合算式并说出理由吗
6天 8天
<
答:8天能修复这段公路。
你能列出综合算式并说出理由吗
( 45 + 40 ) ×8
再乘8,算出甲乙两队8天能修复多少米。
先算甲乙两个工程队每天修多少米。
2
你能列出综合算式并说出理由吗
( 45 + 40 ) ×8
= 85×8
= 680(米)
2
680米 510米
>
答:8天能修复这段公路。
怎样判断在规定时间内是否能完成任务
一是看完成任务的时间是否少于或等于规定的时间。
二是看规定时间内完成的任务量是否大于或等于规定的任务量。
1
2
修复完这段公路时,甲队比乙队多修了多少米?
修复完这段公路时,甲乙两队共用了多少天
我们甲队每天修45米。
我们乙队每天修40米。
甲乙两队同时修复完这段公路时用了6天。
45 × 6 - 40× 6
先算出甲队6天修多少米。
再算出乙队6天修多少米。
1
最后算出甲队比乙队多修了多少米。
你能列出综合算式并说出理由吗
45 × 6 - 40× 6
= 270 - 240
= 30(米)
1
你能列出综合算式并说出理由吗
你能列出综合算式并说出理由吗
( 45 - 40 ) ×6
再乘6,算出6天甲队比乙队多修多少米。
先算出每天甲队比乙队多修多少米。
2
你能列出综合算式并说出理由吗
( 45 - 40 ) ×6
= 5×6
= 30(米)
2
答:甲队比乙队多修了30米。
课堂练习
1. 根据下面的信息列出算式,再议一议。
(1) 甲车每时行40km。乙车每时行50km。
两车从相距720km的两地同时出发,相向而行。经过几时相遇?
720÷ ( 40 + 50 )
= 720÷90
= 8 (时)
答:经过8时相遇。
(教材第21页课堂活动第2题)
1. 根据下面的信息列出算式,再议一议。
(2) 小红每分打44个字。小明每分打36个字。
他们共同打480个字,需要多少分?
480÷ ( 44 + 36 )
= 480÷80
= 6 (分)
答:需要6分。
(教材第21页课堂活动第2题)
议一议:
这两个问题有什么共同点?解决的方法都是什么?
共同点:
这两个问题的共同点都是完成一项任务,
求需要的时间。
解决的方法:
都是用总量(总路程)除以它们的效率和(速度和)求出时间。
(教材第21页课堂活动第2题)
2. 两辆货车运化肥,小货车每次载重3吨,大货车
每次载重6吨。如果两辆车都运了24次,共运化
肥多少吨?
( 3 + 6 ) ×24
= 9×24
= 216(吨)
答:共运化肥216吨。
(教材第22页练习六第3题)
3. 用简便方法计算。
23×34 + 77× 34 52×48 -28×52
= ( 23 + 77 ) ×34
= 100×34
= 3400
= 52×( 48 - 28 )
= 52×20
= 1040
(教材第22页练习六第4题)
3. 用简便方法计算。
9×48 + 48 125×64
= ( 9 + 1 ) ×48
= 10×48
= 480
= 125×
= 1000×8
= 8000
×1
64
8×8
(教材第22页练习六第4题)
3. 用简便方法计算。
102×36 ( 100 - 4 ) ×25
= ( 100 + 2 )
= 100×36 + 2×36
= 3600 + 72
= 100×25 - 4×25
= 2500-100
= 2400
102
×36
= 3672
(教材第22页练习六第4题)
4. 两个工程队从山的两面同时开工挖隧道(如下
图)。15天能够完成这项工程吗?
784÷( 24 + 25 )
答:15天不能够完成这项工程。
= 784÷49
= 16 (天)
16天 15天
>
(教材第22页练习六第5题)
每天挖24米。
每天挖25米。
784m
课堂小结
工效
问题
这节课你有什么收获?
解决问题(2)
一是看完成任务的时间是否少于或等于规定的时间。
二是看规定时间内完成的任务量是否大于或等于规定的任务量。
02
01
课后作业
相关练习。
练习六第3~5题和第7题。
西师版数学四年级(下)
第7课时 解决问题(2)
乘除法的关系和乘法运算律
二
1. 经历解决数学问题的过程,进一步体会具有相遇问题特征的数学问题(工作效率问题)在实际生活中的应用,培养分析、解决问题的能力。
2. 在与他人合作、交流的基础上,体会解决问题策略的多样性。
3. 在解决问题的过程中,感受成功的体验,激发分析、解决问题的兴趣。
学习目标
【重难点】
能分析数量关系,选择解决问题的策略,分析具
有相遇问题特征的数学问题(工作效率问题)的
数量关系。
【重难点】
运用多种策略解决实际问题。
课堂导入
一辆客车和一辆货车同时从两个城市相对开出,客
车平均速度是每时55km,货车平均速度是每时45km。
两车开出5时后相遇,两个城市相距多少千米?
路程 = 速度(和) × 时间
( 55 + 45 ) ×5
答:两个城市相距500千米。
= 100×5
= 500 (千米)
2. 一辆客车和一辆货车同时从相距500km的两个城市相对开出,客车平均速度是每时55km,货车平均
速度是每时45km。两车开出几时后相遇?
时间 = 路程÷速度(和)
500÷ (55 + 45 )
答:两车开出5时后相遇。
= 500÷100
= 5(时)
探究新知
甲、乙两个工程队修复一段510m长的公路,两队同时各从一端开工。8天能否修复这段公路?
说一说从题中你了解到哪些数学信息 需要解决什么数学问题
我们甲队每天修45米。
我们乙队每天修40米。
1
这道题与复习题2对比,你有什么发现
这道题与复习题2很像,复习题2是相遇问题,而这道题是两个工程队修路的工作效率问题。
这两道题都是知道总的路程和两车(队)的速度,求他们的相遇时间(修复完这段公路的时间)。
要求“8天能否修复这段公路”,你的解题思路是怎样的
可以先算出两队合修这段公路需要多少天,再与8天进行比较,进行判断。
也可以先算出两个队8天修复的公路,再与公路总长进行比较,进行判断。
510÷ ( 45 + 40 )
再算两队修复510米的公路需要多少天。
先算甲乙两个工程队每天修多少米。
1
你能列出综合算式并说出理由吗
510÷ ( 45 + 40 )
= 510÷85
= 6 (天)
1
你能列出综合算式并说出理由吗
6天 8天
<
答:8天能修复这段公路。
你能列出综合算式并说出理由吗
( 45 + 40 ) ×8
再乘8,算出甲乙两队8天能修复多少米。
先算甲乙两个工程队每天修多少米。
2
你能列出综合算式并说出理由吗
( 45 + 40 ) ×8
= 85×8
= 680(米)
2
680米 510米
>
答:8天能修复这段公路。
怎样判断在规定时间内是否能完成任务
一是看完成任务的时间是否少于或等于规定的时间。
二是看规定时间内完成的任务量是否大于或等于规定的任务量。
1
2
修复完这段公路时,甲队比乙队多修了多少米?
修复完这段公路时,甲乙两队共用了多少天
我们甲队每天修45米。
我们乙队每天修40米。
甲乙两队同时修复完这段公路时用了6天。
45 × 6 - 40× 6
先算出甲队6天修多少米。
再算出乙队6天修多少米。
1
最后算出甲队比乙队多修了多少米。
你能列出综合算式并说出理由吗
45 × 6 - 40× 6
= 270 - 240
= 30(米)
1
你能列出综合算式并说出理由吗
你能列出综合算式并说出理由吗
( 45 - 40 ) ×6
再乘6,算出6天甲队比乙队多修多少米。
先算出每天甲队比乙队多修多少米。
2
你能列出综合算式并说出理由吗
( 45 - 40 ) ×6
= 5×6
= 30(米)
2
答:甲队比乙队多修了30米。
课堂练习
1. 根据下面的信息列出算式,再议一议。
(1) 甲车每时行40km。乙车每时行50km。
两车从相距720km的两地同时出发,相向而行。经过几时相遇?
720÷ ( 40 + 50 )
= 720÷90
= 8 (时)
答:经过8时相遇。
(教材第21页课堂活动第2题)
1. 根据下面的信息列出算式,再议一议。
(2) 小红每分打44个字。小明每分打36个字。
他们共同打480个字,需要多少分?
480÷ ( 44 + 36 )
= 480÷80
= 6 (分)
答:需要6分。
(教材第21页课堂活动第2题)
议一议:
这两个问题有什么共同点?解决的方法都是什么?
共同点:
这两个问题的共同点都是完成一项任务,
求需要的时间。
解决的方法:
都是用总量(总路程)除以它们的效率和(速度和)求出时间。
(教材第21页课堂活动第2题)
2. 两辆货车运化肥,小货车每次载重3吨,大货车
每次载重6吨。如果两辆车都运了24次,共运化
肥多少吨?
( 3 + 6 ) ×24
= 9×24
= 216(吨)
答:共运化肥216吨。
(教材第22页练习六第3题)
3. 用简便方法计算。
23×34 + 77× 34 52×48 -28×52
= ( 23 + 77 ) ×34
= 100×34
= 3400
= 52×( 48 - 28 )
= 52×20
= 1040
(教材第22页练习六第4题)
3. 用简便方法计算。
9×48 + 48 125×64
= ( 9 + 1 ) ×48
= 10×48
= 480
= 125×
= 1000×8
= 8000
×1
64
8×8
(教材第22页练习六第4题)
3. 用简便方法计算。
102×36 ( 100 - 4 ) ×25
= ( 100 + 2 )
= 100×36 + 2×36
= 3600 + 72
= 100×25 - 4×25
= 2500-100
= 2400
102
×36
= 3672
(教材第22页练习六第4题)
4. 两个工程队从山的两面同时开工挖隧道(如下
图)。15天能够完成这项工程吗?
784÷( 24 + 25 )
答:15天不能够完成这项工程。
= 784÷49
= 16 (天)
16天 15天
>
(教材第22页练习六第5题)
每天挖24米。
每天挖25米。
784m
课堂小结
工效
问题
这节课你有什么收获?
解决问题(2)
一是看完成任务的时间是否少于或等于规定的时间。
二是看规定时间内完成的任务量是否大于或等于规定的任务量。
02
01
课后作业
相关练习。
练习六第3~5题和第7题。
