【人教版】九年级下册 数学 第27章《图形的相似》检测题(含答案)
文档属性
| 名称 | 【人教版】九年级下册 数学 第27章《图形的相似》检测题(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 214.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-08 00:00:00 | ||
图片预览

文档简介
九年级下册 数学
第27章《图形的相似》检测题
一、选择题(每小题3分,共30分)
1、下列说法正确的是 ( )
A.对应边都成比例的多边形相似; B.对应角都相等的多边形相似;
C.边数相同的正多边形相似; D.矩形都相似;
2、如果两个相似多边形面积的比为1:5,则它们的相似比为 ( )
A.1:25; B.1:5; C.1:2.5; D.1:;
3、如图,在△ABC 中,点 D、E 分别在边AB、AC 上,且
则S△ADE∶S四边形BCED = ( )
A. 1∶; B. 1:2; C. 1:3; D. 1:4;
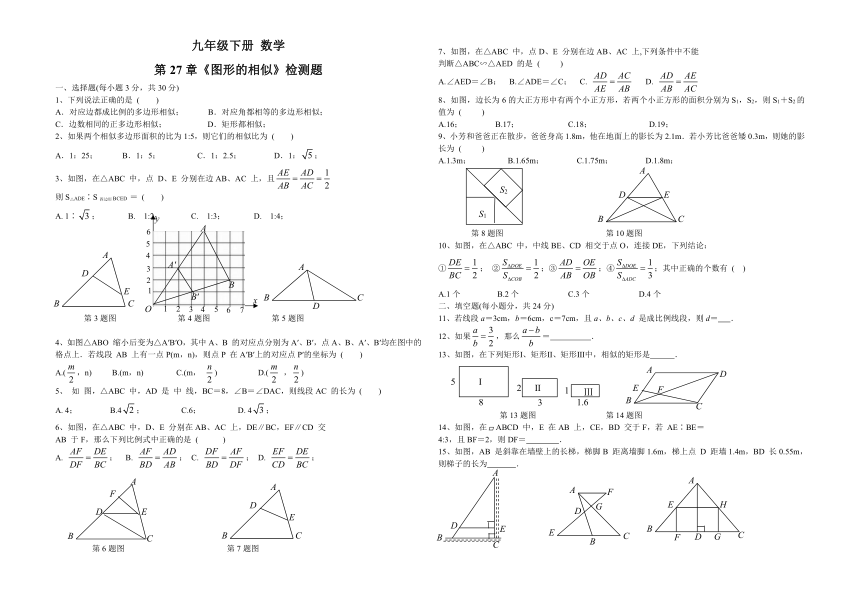
第3题图 第4题图 第5题图
4、如图△ABO 缩小后变为△A′B′O,其中A、B 的对应点分别为A′、B′,点A、B、A′、B′均在图中的格点上.若线段 AB 上有一点P(m,n),则点P 在A′B′上的对应点P′的坐标为 ( )
A.(,n) B.(m,n) C.(m, ) D.( ,)
5、 如 图,△ABC 中,AD 是 中 线,BC=8,∠B=∠DAC,则线段AC 的长为 ( )
A. 4; B.4; C.6; D. 4;
6、如图,在△ABC 中,D、E 分别在AB、AC 上,DE∥BC,EF∥CD 交
AB 于F,那么下列比例式中正确的是 ( )
A. ; B. ; C. ; D. ;
第6题图 第7题图
7、如图,在△ABC 中,点D、E 分别在边AB、AC 上,下列条件中不能
判断△ABC∽△AED 的是 ( )
A.∠AED=∠B; B.∠ADE=∠C; C. D.
8、如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为 ( )
A.16; B.17; C.18; D.19;
9、小芳和爸爸正在散步,爸爸身高1.8m,他在地面上的影长为2.1m.若小芳比爸爸矮0.3m,则她的影长为 ( )
A.1.3m; B.1.65m; C.1.75m; D.1.8m;
第8题图 第10题图
10、如图,在△ABC 中,中线BE、CD 相交于点O,连接DE,下列结论:
①; ②;③;④;其中正确的个数有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题分,共24分)
11、若线段a=3cm,b=6cm,c=7cm,且a、b、c、d 是成比例线段,则d= .
12、如果,那么= .
13、如图,在下列矩形Ⅰ、矩形Ⅱ、矩形Ⅲ中,相似的矩形是 .
第13题图 第14题图
14、如图,在ABCD 中,E 在AB 上,CE,BD 交于F,若 AE∶BE=
4:3,且BF=2,则DF= .
15、如图,AB 是斜靠在墙壁上的长梯,梯脚B 距离墙脚1.6m,梯上点 D 距墙1.4m,BD 长0.55m,则梯子的长为 .
第15题图 第16题图 第17题图
16、如图,已知点 D 是AB 边的中点,AF∥BC,CG∶AG=3:1,BC=8,则AF= .
17、如图,矩形EFGH 内接于△ABC,且边FG 落在BC 上,若AD⊥BC,BC=3,AD=2,EF=EH,那么 EH 的长为 .
18、已知直线y=-x+2与x 轴交于点A,与y 轴交于点B,在x轴上有一点C,使B,O,C 三点构成的三角形与△AOB 相似,则点C 的坐标为 .
三、解答题(共46分)
19、(4分)如图,△ABC 与△A′B′C′是位似图形,且位似比是1:2,若AB=2cm,则A′B′= cm,并在图中画出位似中心O.
20、(6分)已知△ABC∽△DEF,且AB=2DE,若△ABC 的周长为12cm,△DEF 的面积为8cm2,求△ABC的面积和△DEF 的周长.
21、(10分)如图,△ABC 是等边三角形,CE 是外角平分线,点 D 在AC 上,连接BD 并延长交CE 于点E.
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE 的长.
22、(8分)如 图,在 四 边 形 ABCD 中,AC 平 分∠BCD,AC⊥AB,
E 是BC 的中点,AD⊥AE.求证:AC2=CD·BC.
23、、(8分)如图,某校数学兴趣小组利用自制的直角三角形硬纸板 DEF 来测量操场旗杆AB 的 高 度,他 们 通 过 调 整 测 量 位置,使斜边 DF 与地面保持平行,并使边DE=0.5米,EF=0.25米,目测点 D 到地面的距离DG=1.5米,到旗杆的水平距离 DC=20米,求旗杆的高度.
24(10分)如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且
(1)求证:△ADF∽△ACG;
(2)若 ,求 的值.
参考答案:
1、C ;2、D ;3、C ;4、D ;5、B; 6、D ;7、D ;8、B ;9、C ;10、B ;11、14cm ;12、;13、Ⅰ与Ⅲ;14、;15、4.4m; 16、4;17、;18、(1,0)或(-1,0)或(-4,0); 19、4;图略;
20、设△ABC 的面积为x cm2,△DEF 的周长为y cm,∵AB=2DE,∴=2,∵△ABC∽△DEF,∴=22,=2,得x=32,y=6.
21、(1)证明:∵CD 是边AB 上的高,∴∠ADC=∠CDB=90°.
又∴△ACD∽△CBD.
(2)∵△ACD∽△CBD,∴∠A=∠BCD.在△ACD 中,∠ADC=90°.
∴∠A+∠ACD=90°,∴∠BCD+∠ACD=90°,即∠ACB=90°.
22、由题意可知△DEF∽△DCA,∴ ∴AC==10(米),
∴AB=AC+BC=10+1.5=11.5(米). ∴旗杆高为11.5米.
23、证明:∵AC 平分∠BCD,∴∠DCA=∠ACB,又∵AC⊥AB,AD⊥AE,
∴ ∠DAC+ ∠CAE=90°,∠CAE+∠EAB=90°,
∴∠DAC=∠EAB.又∵E 是BC 的中点,∴AE=BE,
∴∠EAB=∠ABC,∴∠DAC=∠ABC,∴△ACD∽△BCA,
∴, ∴AC2=CD·BC.
24、(1)证明:∵△ABC 是等边三角形,∴∠ACB=∠A=60°,
∴∠ACF=120°.∵CE 平分∠ACF,∴∠ACE=60°.
∴∠A=∠ACE.又∵∠ADB=∠CDE,∴△ABD∽△CED;
(2)∵△ABD∽△CED,AD=2CD,∴AB=2,∴CE=3.
过E 作EG⊥BF 于G,在 Rt△CEG 中,∠ECG=60°,CE=3,
∴CG=,EG=,在 Rt△BEG 中,BG=BC+CG=6+=,
∴BE=
25、(1)如图,作CE⊥AB 于点E,∵CD∥AB,DA⊥AB,∴四边形AECD 是矩形,∴AE=CD=5,CE=AD=4,∴BE=AB-AE=3.
在 Rt△CBE 中,BC=5,∴t=5(s),即当t=,5s,P、Q 两点同时停止运动.
(2)若BP=BQ,则t=8-t,∴t=4s;若QP=QB,则,
若PQ=PB,则t=,
综合以上,当t等于为上述三种情况时,△PQB 为等腰三角形.
1
1
2
2
3
3
4
4
5
5
6
6
7
A
B
O
B′
A′
x
y
A
B
C
D
E
A
B
C
D
A
B
C
D
E
F
A
B
C
D
E
A
B
C
D
E
S1
S2
A
B
C
D
E
F
5
8
2
3
1
1.6
Ⅰ
Ⅱ
Ⅲ
A
B
C
D
E
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
A
B
C
A′
B′
C′
F
A
B
C
D
E
A
B
C
D
E
F
G
第27章《图形的相似》检测题
一、选择题(每小题3分,共30分)
1、下列说法正确的是 ( )
A.对应边都成比例的多边形相似; B.对应角都相等的多边形相似;
C.边数相同的正多边形相似; D.矩形都相似;
2、如果两个相似多边形面积的比为1:5,则它们的相似比为 ( )
A.1:25; B.1:5; C.1:2.5; D.1:;
3、如图,在△ABC 中,点 D、E 分别在边AB、AC 上,且
则S△ADE∶S四边形BCED = ( )
A. 1∶; B. 1:2; C. 1:3; D. 1:4;
第3题图 第4题图 第5题图
4、如图△ABO 缩小后变为△A′B′O,其中A、B 的对应点分别为A′、B′,点A、B、A′、B′均在图中的格点上.若线段 AB 上有一点P(m,n),则点P 在A′B′上的对应点P′的坐标为 ( )
A.(,n) B.(m,n) C.(m, ) D.( ,)
5、 如 图,△ABC 中,AD 是 中 线,BC=8,∠B=∠DAC,则线段AC 的长为 ( )
A. 4; B.4; C.6; D. 4;
6、如图,在△ABC 中,D、E 分别在AB、AC 上,DE∥BC,EF∥CD 交
AB 于F,那么下列比例式中正确的是 ( )
A. ; B. ; C. ; D. ;
第6题图 第7题图
7、如图,在△ABC 中,点D、E 分别在边AB、AC 上,下列条件中不能
判断△ABC∽△AED 的是 ( )
A.∠AED=∠B; B.∠ADE=∠C; C. D.
8、如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为 ( )
A.16; B.17; C.18; D.19;
9、小芳和爸爸正在散步,爸爸身高1.8m,他在地面上的影长为2.1m.若小芳比爸爸矮0.3m,则她的影长为 ( )
A.1.3m; B.1.65m; C.1.75m; D.1.8m;
第8题图 第10题图
10、如图,在△ABC 中,中线BE、CD 相交于点O,连接DE,下列结论:
①; ②;③;④;其中正确的个数有 ( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题分,共24分)
11、若线段a=3cm,b=6cm,c=7cm,且a、b、c、d 是成比例线段,则d= .
12、如果,那么= .
13、如图,在下列矩形Ⅰ、矩形Ⅱ、矩形Ⅲ中,相似的矩形是 .
第13题图 第14题图
14、如图,在ABCD 中,E 在AB 上,CE,BD 交于F,若 AE∶BE=
4:3,且BF=2,则DF= .
15、如图,AB 是斜靠在墙壁上的长梯,梯脚B 距离墙脚1.6m,梯上点 D 距墙1.4m,BD 长0.55m,则梯子的长为 .
第15题图 第16题图 第17题图
16、如图,已知点 D 是AB 边的中点,AF∥BC,CG∶AG=3:1,BC=8,则AF= .
17、如图,矩形EFGH 内接于△ABC,且边FG 落在BC 上,若AD⊥BC,BC=3,AD=2,EF=EH,那么 EH 的长为 .
18、已知直线y=-x+2与x 轴交于点A,与y 轴交于点B,在x轴上有一点C,使B,O,C 三点构成的三角形与△AOB 相似,则点C 的坐标为 .
三、解答题(共46分)
19、(4分)如图,△ABC 与△A′B′C′是位似图形,且位似比是1:2,若AB=2cm,则A′B′= cm,并在图中画出位似中心O.
20、(6分)已知△ABC∽△DEF,且AB=2DE,若△ABC 的周长为12cm,△DEF 的面积为8cm2,求△ABC的面积和△DEF 的周长.
21、(10分)如图,△ABC 是等边三角形,CE 是外角平分线,点 D 在AC 上,连接BD 并延长交CE 于点E.
(1)求证:△ABD∽△CED;
(2)若AB=6,AD=2CD,求BE 的长.
22、(8分)如 图,在 四 边 形 ABCD 中,AC 平 分∠BCD,AC⊥AB,
E 是BC 的中点,AD⊥AE.求证:AC2=CD·BC.
23、、(8分)如图,某校数学兴趣小组利用自制的直角三角形硬纸板 DEF 来测量操场旗杆AB 的 高 度,他 们 通 过 调 整 测 量 位置,使斜边 DF 与地面保持平行,并使边DE=0.5米,EF=0.25米,目测点 D 到地面的距离DG=1.5米,到旗杆的水平距离 DC=20米,求旗杆的高度.
24(10分)如图,在△ABC中,点D,E分别在边AB,AC上,∠AED=∠B,射线AG分别交线段DE,BC于点F,G,且
(1)求证:△ADF∽△ACG;
(2)若 ,求 的值.
参考答案:
1、C ;2、D ;3、C ;4、D ;5、B; 6、D ;7、D ;8、B ;9、C ;10、B ;11、14cm ;12、;13、Ⅰ与Ⅲ;14、;15、4.4m; 16、4;17、;18、(1,0)或(-1,0)或(-4,0); 19、4;图略;
20、设△ABC 的面积为x cm2,△DEF 的周长为y cm,∵AB=2DE,∴=2,∵△ABC∽△DEF,∴=22,=2,得x=32,y=6.
21、(1)证明:∵CD 是边AB 上的高,∴∠ADC=∠CDB=90°.
又∴△ACD∽△CBD.
(2)∵△ACD∽△CBD,∴∠A=∠BCD.在△ACD 中,∠ADC=90°.
∴∠A+∠ACD=90°,∴∠BCD+∠ACD=90°,即∠ACB=90°.
22、由题意可知△DEF∽△DCA,∴ ∴AC==10(米),
∴AB=AC+BC=10+1.5=11.5(米). ∴旗杆高为11.5米.
23、证明:∵AC 平分∠BCD,∴∠DCA=∠ACB,又∵AC⊥AB,AD⊥AE,
∴ ∠DAC+ ∠CAE=90°,∠CAE+∠EAB=90°,
∴∠DAC=∠EAB.又∵E 是BC 的中点,∴AE=BE,
∴∠EAB=∠ABC,∴∠DAC=∠ABC,∴△ACD∽△BCA,
∴, ∴AC2=CD·BC.
24、(1)证明:∵△ABC 是等边三角形,∴∠ACB=∠A=60°,
∴∠ACF=120°.∵CE 平分∠ACF,∴∠ACE=60°.
∴∠A=∠ACE.又∵∠ADB=∠CDE,∴△ABD∽△CED;
(2)∵△ABD∽△CED,AD=2CD,∴AB=2,∴CE=3.
过E 作EG⊥BF 于G,在 Rt△CEG 中,∠ECG=60°,CE=3,
∴CG=,EG=,在 Rt△BEG 中,BG=BC+CG=6+=,
∴BE=
25、(1)如图,作CE⊥AB 于点E,∵CD∥AB,DA⊥AB,∴四边形AECD 是矩形,∴AE=CD=5,CE=AD=4,∴BE=AB-AE=3.
在 Rt△CBE 中,BC=5,∴t=5(s),即当t=,5s,P、Q 两点同时停止运动.
(2)若BP=BQ,则t=8-t,∴t=4s;若QP=QB,则,
若PQ=PB,则t=,
综合以上,当t等于为上述三种情况时,△PQB 为等腰三角形.
1
1
2
2
3
3
4
4
5
5
6
6
7
A
B
O
B′
A′
x
y
A
B
C
D
E
A
B
C
D
A
B
C
D
E
F
A
B
C
D
E
A
B
C
D
E
S1
S2
A
B
C
D
E
F
5
8
2
3
1
1.6
Ⅰ
Ⅱ
Ⅲ
A
B
C
D
E
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
A
B
C
A′
B′
C′
F
A
B
C
D
E
A
B
C
D
E
F
G
