近两年(2020-2021)高考数学 真题分类汇编-概率与统计(含解析)
文档属性
| 名称 | 近两年(2020-2021)高考数学 真题分类汇编-概率与统计(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 419.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 00:00:00 | ||
图片预览



文档简介
2020-2021真题汇编-概率与统计
考点一:统计-直方图
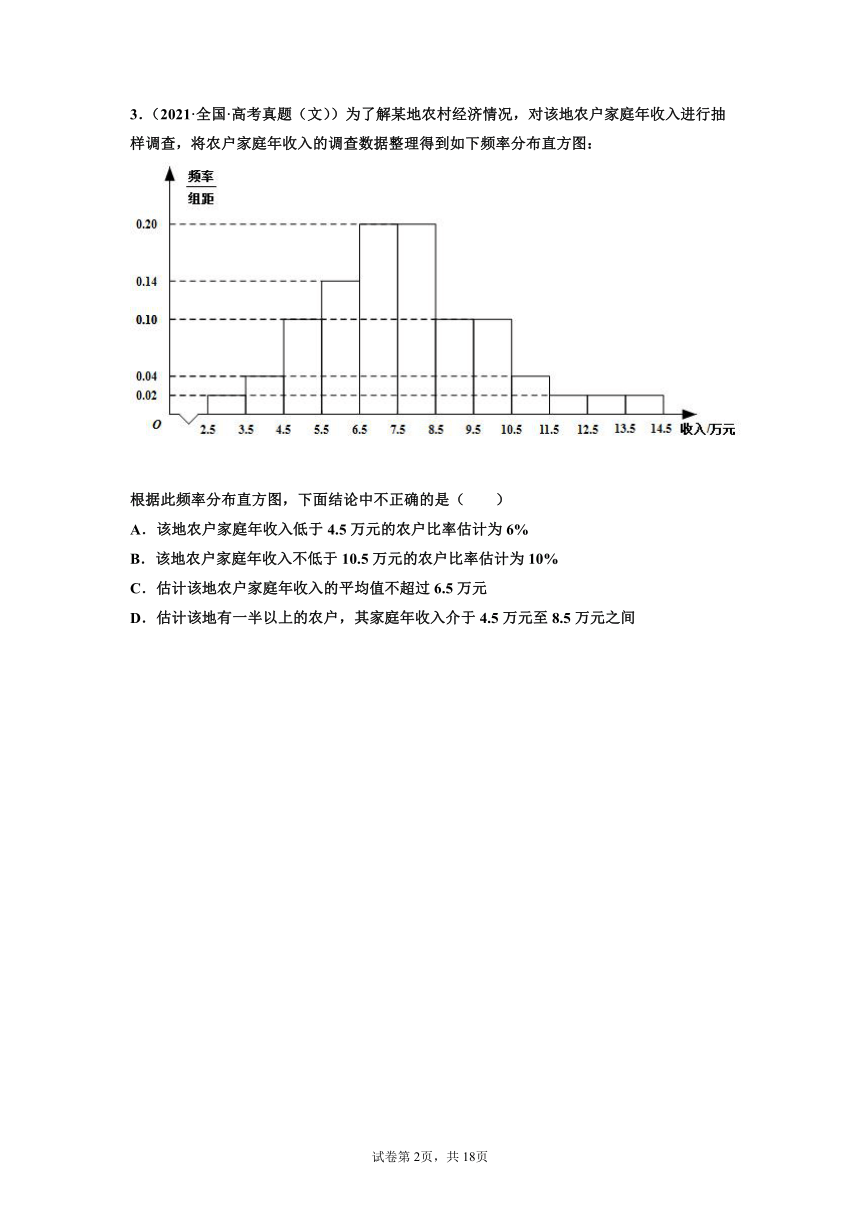
1.(2021·天津·高考真题)从某网络平台推荐的影视作品中抽取部,统计其评分数据,将所得个评分数据分为组:、、、,并整理得到如下的频率分布直方图,则评分在区间内的影视作品数量是( )
A. B. C. D.
2.(2020·天津·高考真题)从一批零件中抽取80个,测量其直径(单位:),将所得数据分为9组:,并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间内的个数为( )
A.10 B.18 C.20 D.36
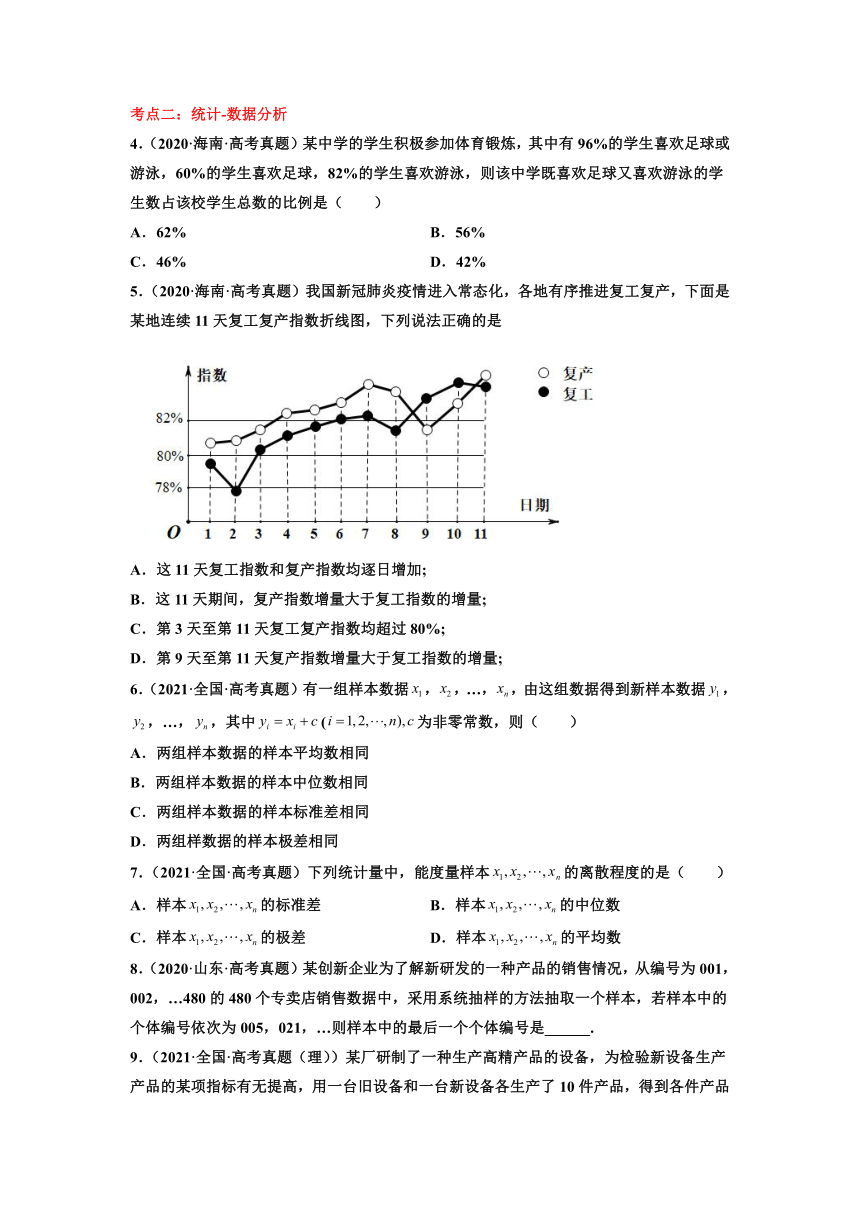
3.(2021·全国·高考真题(文))为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
考点二:统计-数据分析
4.(2020·海南·高考真题)某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62% B.56%
C.46% D.42%
5.(2020·海南·高考真题)我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是
A.这11天复工指数和复产指数均逐日增加;
B.这11天期间,复产指数增量大于复工指数的增量;
C.第3天至第11天复工复产指数均超过80%;
D.第9天至第11天复产指数增量大于复工指数的增量;
6.(2021·全国·高考真题)有一组样本数据,,…,,由这组数据得到新样本数据,,…,,其中(为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样数据的样本极差相同
7.(2021·全国·高考真题)下列统计量中,能度量样本的离散程度的是( )
A.样本的标准差 B.样本的中位数
C.样本的极差 D.样本的平均数
8.(2020·山东·高考真题)某创新企业为了解新研发的一种产品的销售情况,从编号为001,002,…480的480个专卖店销售数据中,采用系统抽样的方法抽取一个样本,若样本中的个体编号依次为005,021,…则样本中的最后一个个体编号是______.
9.(2021·全国·高考真题(理))某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 9.8 10.3 10.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7
新设备 10.1 10.4 10.1 10.0 10.1 10.3 10.6 10.5 10.4 10.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为和.
(1)求,,,;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
考点三:计数原理
10.(2020·北京·高考真题)在的展开式中,的系数为( ).
A. B.5 C. D.10
11.(2020·山东·高考真题)在的二项展开式中,第项的二项式系数是( )
A. B. C. D.
12.(2020·全国·高考真题(理))的展开式中x3y3的系数为( )
A.5 B.10
C.15 D.20
【答案】C
13.(2020·全国·高考真题(理))的展开式中常数项是__________(用数字作答).
14.(2020·天津·高考真题)在的展开式中,的系数是_________.
15.(2021·浙江·高考真题)已知多项式,则___________,___________.
16.(2020·浙江·高考真题)设,则________;________.
17.(2020·海南·高考真题)6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有( )
A.120种 B.90种
C.60种 D.30种
18.(2020·海南·高考真题)要安排3名学生到2个乡村做志愿者,每名学生只能选择去一个村,每个村里至少有一名志愿者,则不同的安排方法共有( )
A.2种 B.3种 C.6种 D.8种
19.(2021·全国·高考真题(理))将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有( )
A.60种 B.120种 C.240种 D.480种
20.(2020·山东·高考真题)现从4名男生和3名女生中,任选3名男生和2名女生,分别担任5门不同学科的课代表,则不同安排方法的种数是( )
A.12 B.120 C.1440 D.17280
21.(2020·全国·高考真题(理))4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,则不同的安排方法共有__________种.
2020-2021真题汇编-概率与统计(一)
解析版
考点一:统计-直方图
1.(2021·天津·高考真题)从某网络平台推荐的影视作品中抽取部,统计其评分数据,将所得个评分数据分为组:、、、,并整理得到如下的频率分布直方图,则评分在区间内的影视作品数量是( )
A. B. C. D.
【答案】D
【分析】
利用频率分布直方图可计算出评分在区间内的影视作品数量.
【详解】
由频率分布直方图可知,评分在区间内的影视作品数量为.
故选:D.
2.(2020·天津·高考真题)从一批零件中抽取80个,测量其直径(单位:),将所得数据分为9组:,并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间内的个数为( )
A.10 B.18 C.20 D.36
【答案】B
【分析】
根据直方图确定直径落在区间之间的零件频率,然后结合样本总数计算其个数即可.
【详解】
根据直方图,直径落在区间之间的零件频率为:,
则区间内零件的个数为:.
故选:B.
【点睛】
本题主要考查频率分布直方图的计算与实际应用,属于中等题.
3.(2021·全国·高考真题(文))为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
【答案】C
【分析】
根据直方图的意义直接计算相应范围内的频率,即可判定ABD,以各组的中间值作为代表乘以相应的频率,然后求和即得到样本的平均数的估计值,也就是总体平均值的估计值,计算后即可判定C.
【详解】
因为频率直方图中的组距为1,所以各组的直方图的高度等于频率.样本频率直方图中的频率即可作为总体的相应比率的估计值.
该地农户家庭年收入低于4.5万元的农户的比率估计值为,故A正确;
该地农户家庭年收入不低于10.5万元的农户比率估计值为,故B正确;
该地农户家庭年收入介于4.5万元至8.5万元之间的比例估计值为,故D正确;
该地农户家庭年收入的平均值的估计值为(万元),超过6.5万元,故C错误.
综上,给出结论中不正确的是C.
故选:C.
【点睛】
本题考查利用样本频率直方图估计总体频率和平均值,属基础题,样本的频率可作为总体的频率的估计值,样本的平均值的估计值是各组的中间值乘以其相应频率然后求和所得值,可以作为总体的平均值的估计值.注意各组的频率等于.
考点二:统计-数据分析
4.(2020·海南·高考真题)某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62% B.56%
C.46% D.42%
【答案】C
【分析】
记“该中学学生喜欢足球”为事件,“该中学学生喜欢游泳”为事件,则“该中学学生喜欢足球或游泳”为事件,“该中学学生既喜欢足球又喜欢游泳”为事件,然后根据积事件的概率公式可得结果.
【详解】
记“该中学学生喜欢足球”为事件,“该中学学生喜欢游泳”为事件,则“该中学学生喜欢足球或游泳”为事件,“该中学学生既喜欢足球又喜欢游泳”为事件,
则,,,
所以
所以该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例为.
故选:C.
【点睛】
本题考查了积事件的概率公式,属于基础题.
5.(2020·海南·高考真题)我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是
A.这11天复工指数和复产指数均逐日增加;
B.这11天期间,复产指数增量大于复工指数的增量;
C.第3天至第11天复工复产指数均超过80%;
D.第9天至第11天复产指数增量大于复工指数的增量;
【答案】CD
【分析】
注意到折线图中有递减部分,可判定A错误;注意考查第1天和第11天的复工复产指数的差的大小,可判定B错误;根据图象,结合复工复产指数的意义和增量的意义可以判定CD正确.
【详解】
由图可知,第1天到第2天复工指数减少,第7天到第8天复工指数减少,第10天到第11复工指数减少,第8天到第9天复产指数减少,故A错误;
由图可知,第一天的复产指标与复工指标的差大于第11天的复产指标与复工指标的差,所以这11天期间,复产指数增量小于复工指数的增量,故B错误;
由图可知,第3天至第11天复工复产指数均超过80%,故C正确;
由图可知,第9天至第11天复产指数增量大于复工指数的增量,故D正确;
【点睛】
本题考查折线图表示的函数的认知与理解,考查理解能力,识图能力,推理能力,难点在于指数增量的理解与观测,属中档题.
6.(2021·全国·高考真题)有一组样本数据,,…,,由这组数据得到新样本数据,,…,,其中(为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样数据的样本极差相同
【答案】CD
【分析】
A、C利用两组数据的线性关系有、,即可判断正误;根据中位数、极差的定义,结合已知线性关系可判断B、D的正误.
【详解】
A:且,故平均数不相同,错误;
B:若第一组中位数为,则第二组的中位数为,显然不相同,错误;
C:,故方差相同,正确;
D:由极差的定义知:若第一组的极差为,则第二组的极差为,故极差相同,正确;
故选:CD
7.(2021·全国·高考真题)下列统计量中,能度量样本的离散程度的是( )
A.样本的标准差 B.样本的中位数
C.样本的极差 D.样本的平均数
【答案】AC
【分析】
考查所给的选项哪些是考查数据的离散程度,哪些是考查数据的集中趋势即可确定正确选项.
【详解】
由标准差的定义可知,标准差考查的是数据的离散程度;
由中位数的定义可知,中位数考查的是数据的集中趋势;
由极差的定义可知,极差考查的是数据的离散程度;
由平均数的定义可知,平均数考查的是数据的集中趋势;
故选:AC.
8.(2020·山东·高考真题)某创新企业为了解新研发的一种产品的销售情况,从编号为001,002,…480的480个专卖店销售数据中,采用系统抽样的方法抽取一个样本,若样本中的个体编号依次为005,021,…则样本中的最后一个个体编号是______.
【答案】469
【分析】
先求得编号间隔为16以及样本容量,再由样本中所有数据编号为求解.
【详解】
间隔为021-005=16,
则样本容量为,
样本中所有数据编号为,
所以样本中的最后一个个体的编号为,
故答案为:469
9.(2021·全国·高考真题(理))某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 9.8 10.3 10.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7
新设备 10.1 10.4 10.1 10.0 10.1 10.3 10.6 10.5 10.4 10.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为和.
(1)求,,,;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
【答案】(1);(2)新设备生产产品的该项指标的均值较旧设备有显著提高.
【分析】
(1)根据平均数和方差的计算方法,计算出平均数和方差.
(2)根据题目所给判断依据,结合(1)的结论进行判断.
【详解】
(1),
,
,
.
(2)依题意,,,
,所以新设备生产产品的该项指标的均值较旧设备有显著提高.
考点三:计数原理
10.(2020·北京·高考真题)在的展开式中,的系数为( ).
A. B.5 C. D.10
【答案】C
【分析】
首先写出展开式的通项公式,然后结合通项公式确定的系数即可.
【详解】
展开式的通项公式为:,
令可得:,则的系数为:.
故选:C.
【点睛】
二项式定理的核心是通项公式,求解此类问题可以分两步完成:第一步根据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n和r的隐含条件,即n,r均为非负整数,且n≥r,如常数项指数为零、有理项指数为整数等);第二步是根据所求的指数,再求所求解的项.
11.(2020·山东·高考真题)在的二项展开式中,第项的二项式系数是( )
A. B. C. D.
【答案】A
【分析】
本题可通过二项式系数的定义得出结果.
【详解】
第项的二项式系数为,
故选:A.
12.(2020·全国·高考真题(理))的展开式中x3y3的系数为( )
A.5 B.10
C.15 D.20
【答案】C
【分析】
求得展开式的通项公式为(且),即可求得与展开式的乘积为或形式,对分别赋值为3,1即可求得的系数,问题得解.
【详解】
展开式的通项公式为(且)
所以的各项与展开式的通项的乘积可表示为:
和
在中,令,可得:,该项中的系数为,
在中,令,可得:,该项中的系数为
所以的系数为
故选:C
【点睛】
本题主要考查了二项式定理及其展开式的通项公式,还考查了赋值法、转化能力及分析能力,属于中档题.
13.(2020·全国·高考真题(理))的展开式中常数项是__________(用数字作答).
【答案】
【分析】
写出二项式展开通项,即可求得常数项.
【详解】
其二项式展开通项:
当,解得
的展开式中常数项是:.
故答案为:.
【点睛】
本题考查二项式定理,利用通项公式求二项展开式中的指定项,解题关键是掌握的展开通项公式,考查了分析能力和计算能力,属于基础题.
14.(2020·天津·高考真题)在的展开式中,的系数是_________.
【答案】10
【分析】
写出二项展开式的通项公式,整理后令的指数为2,即可求出.
【详解】
因为的展开式的通项公式为,令,解得.
所以的系数为.
故答案为:.
【点睛】
本题主要考查二项展开式的通项公式的应用,属于基础题.
15.(2021·浙江·高考真题)已知多项式,则___________,___________.
【答案】; .
【分析】
根据二项展开式定理,分别求出的展开式,即可得出结论.
【详解】
,
,
所以,
,
所以.
故答案为:.
16.(2020·浙江·高考真题)设,则________;________.
【答案】
【分析】
利用二项式展开式的通项公式计算即可.
【详解】
的通项为,
令,则,故;
.
故答案为:;.
【点晴】
本题主要考查利用二项式定理求指定项的系数问题,考查学生的数学运算能力,是一道基础题.
17.(2020·海南·高考真题)6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有( )
A.120种 B.90种
C.60种 D.30种
【答案】C
【分析】
分别安排各场馆的志愿者,利用组合计数和乘法计数原理求解.
【详解】
首先从名同学中选名去甲场馆,方法数有;
然后从其余名同学中选名去乙场馆,方法数有;
最后剩下的名同学去丙场馆.
故不同的安排方法共有种.
故选:C
【点睛】
本小题主要考查分步计数原理和组合数的计算,属于基础题.
18.(2020·海南·高考真题)要安排3名学生到2个乡村做志愿者,每名学生只能选择去一个村,每个村里至少有一名志愿者,则不同的安排方法共有( )
A.2种 B.3种 C.6种 D.8种
【答案】C
【分析】
首先将3名学生分成两个组,然后将2组学生安排到2个村即可.
【详解】
第一步,将3名学生分成两个组,有种分法
第二步,将2组学生安排到2个村,有种安排方法
所以,不同的安排方法共有种
故选:C
【点睛】
解答本类问题时一般采取先组后排的策略.
19.(2021·全国·高考真题(理))将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有( )
A.60种 B.120种 C.240种 D.480种
【答案】C
【分析】
先确定有一个项目中分配2名志愿者,其余各项目中分配1名志愿者,然后利用组合,排列,乘法原理求得.
【详解】
根据题意,有一个项目中分配2名志愿者,其余各项目中分配1名志愿者,可以先从5名志愿者中任选2人,组成一个小组,有种选法;然后连同其余三人,看成四个元素,四个项目看成四个不同的位置,四个不同的元素在四个不同的位置的排列方法数有4!种,根据乘法原理,完成这件事,共有种不同的分配方案,
故选:C.
【点睛】
本题考查排列组合的应用问题,属基础题,关键是首先确定人数的分配情况,然后利用先选后排思想求解.
20.(2020·山东·高考真题)现从4名男生和3名女生中,任选3名男生和2名女生,分别担任5门不同学科的课代表,则不同安排方法的种数是( )
A.12 B.120 C.1440 D.17280
【答案】C
【分析】
首先选3名男生和2名女生,再全排列,共有种不同安排方法.
【详解】
首先从4名男生和3名女生中,任选3名男生和2名女生,共有种情况,
再分别担任5门不同学科的课代表,共有种情况.
所以共有种不同安排方法.
故选:C
21.(2020·全国·高考真题(理))4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,则不同的安排方法共有__________种.
【答案】
【分析】
根据题意,有且只有2名同学在同一个小区,利用先选后排的思想,结合排列组合和乘法计数原理得解.
【详解】
4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学
先取2名同学看作一组,选法有:
现在可看成是3组同学分配到3个小区,分法有:
根据分步乘法原理,可得不同的安排方法种
故答案为:.
【点睛】
本题主要考查了计数原理的综合应用,解题关键是掌握分步乘法原理和捆绑法的使用,考查了分析能力和计算能力,属于中档题.
试卷第2页,共2页
考点一:统计-直方图
1.(2021·天津·高考真题)从某网络平台推荐的影视作品中抽取部,统计其评分数据,将所得个评分数据分为组:、、、,并整理得到如下的频率分布直方图,则评分在区间内的影视作品数量是( )
A. B. C. D.
2.(2020·天津·高考真题)从一批零件中抽取80个,测量其直径(单位:),将所得数据分为9组:,并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间内的个数为( )
A.10 B.18 C.20 D.36
3.(2021·全国·高考真题(文))为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
考点二:统计-数据分析
4.(2020·海南·高考真题)某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62% B.56%
C.46% D.42%
5.(2020·海南·高考真题)我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是
A.这11天复工指数和复产指数均逐日增加;
B.这11天期间,复产指数增量大于复工指数的增量;
C.第3天至第11天复工复产指数均超过80%;
D.第9天至第11天复产指数增量大于复工指数的增量;
6.(2021·全国·高考真题)有一组样本数据,,…,,由这组数据得到新样本数据,,…,,其中(为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样数据的样本极差相同
7.(2021·全国·高考真题)下列统计量中,能度量样本的离散程度的是( )
A.样本的标准差 B.样本的中位数
C.样本的极差 D.样本的平均数
8.(2020·山东·高考真题)某创新企业为了解新研发的一种产品的销售情况,从编号为001,002,…480的480个专卖店销售数据中,采用系统抽样的方法抽取一个样本,若样本中的个体编号依次为005,021,…则样本中的最后一个个体编号是______.
9.(2021·全国·高考真题(理))某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 9.8 10.3 10.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7
新设备 10.1 10.4 10.1 10.0 10.1 10.3 10.6 10.5 10.4 10.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为和.
(1)求,,,;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
考点三:计数原理
10.(2020·北京·高考真题)在的展开式中,的系数为( ).
A. B.5 C. D.10
11.(2020·山东·高考真题)在的二项展开式中,第项的二项式系数是( )
A. B. C. D.
12.(2020·全国·高考真题(理))的展开式中x3y3的系数为( )
A.5 B.10
C.15 D.20
【答案】C
13.(2020·全国·高考真题(理))的展开式中常数项是__________(用数字作答).
14.(2020·天津·高考真题)在的展开式中,的系数是_________.
15.(2021·浙江·高考真题)已知多项式,则___________,___________.
16.(2020·浙江·高考真题)设,则________;________.
17.(2020·海南·高考真题)6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有( )
A.120种 B.90种
C.60种 D.30种
18.(2020·海南·高考真题)要安排3名学生到2个乡村做志愿者,每名学生只能选择去一个村,每个村里至少有一名志愿者,则不同的安排方法共有( )
A.2种 B.3种 C.6种 D.8种
19.(2021·全国·高考真题(理))将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有( )
A.60种 B.120种 C.240种 D.480种
20.(2020·山东·高考真题)现从4名男生和3名女生中,任选3名男生和2名女生,分别担任5门不同学科的课代表,则不同安排方法的种数是( )
A.12 B.120 C.1440 D.17280
21.(2020·全国·高考真题(理))4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,则不同的安排方法共有__________种.
2020-2021真题汇编-概率与统计(一)
解析版
考点一:统计-直方图
1.(2021·天津·高考真题)从某网络平台推荐的影视作品中抽取部,统计其评分数据,将所得个评分数据分为组:、、、,并整理得到如下的频率分布直方图,则评分在区间内的影视作品数量是( )
A. B. C. D.
【答案】D
【分析】
利用频率分布直方图可计算出评分在区间内的影视作品数量.
【详解】
由频率分布直方图可知,评分在区间内的影视作品数量为.
故选:D.
2.(2020·天津·高考真题)从一批零件中抽取80个,测量其直径(单位:),将所得数据分为9组:,并整理得到如下频率分布直方图,则在被抽取的零件中,直径落在区间内的个数为( )
A.10 B.18 C.20 D.36
【答案】B
【分析】
根据直方图确定直径落在区间之间的零件频率,然后结合样本总数计算其个数即可.
【详解】
根据直方图,直径落在区间之间的零件频率为:,
则区间内零件的个数为:.
故选:B.
【点睛】
本题主要考查频率分布直方图的计算与实际应用,属于中等题.
3.(2021·全国·高考真题(文))为了解某地农村经济情况,对该地农户家庭年收入进行抽样调查,将农户家庭年收入的调查数据整理得到如下频率分布直方图:
根据此频率分布直方图,下面结论中不正确的是( )
A.该地农户家庭年收入低于4.5万元的农户比率估计为6%
B.该地农户家庭年收入不低于10.5万元的农户比率估计为10%
C.估计该地农户家庭年收入的平均值不超过6.5万元
D.估计该地有一半以上的农户,其家庭年收入介于4.5万元至8.5万元之间
【答案】C
【分析】
根据直方图的意义直接计算相应范围内的频率,即可判定ABD,以各组的中间值作为代表乘以相应的频率,然后求和即得到样本的平均数的估计值,也就是总体平均值的估计值,计算后即可判定C.
【详解】
因为频率直方图中的组距为1,所以各组的直方图的高度等于频率.样本频率直方图中的频率即可作为总体的相应比率的估计值.
该地农户家庭年收入低于4.5万元的农户的比率估计值为,故A正确;
该地农户家庭年收入不低于10.5万元的农户比率估计值为,故B正确;
该地农户家庭年收入介于4.5万元至8.5万元之间的比例估计值为,故D正确;
该地农户家庭年收入的平均值的估计值为(万元),超过6.5万元,故C错误.
综上,给出结论中不正确的是C.
故选:C.
【点睛】
本题考查利用样本频率直方图估计总体频率和平均值,属基础题,样本的频率可作为总体的频率的估计值,样本的平均值的估计值是各组的中间值乘以其相应频率然后求和所得值,可以作为总体的平均值的估计值.注意各组的频率等于.
考点二:统计-数据分析
4.(2020·海南·高考真题)某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( )
A.62% B.56%
C.46% D.42%
【答案】C
【分析】
记“该中学学生喜欢足球”为事件,“该中学学生喜欢游泳”为事件,则“该中学学生喜欢足球或游泳”为事件,“该中学学生既喜欢足球又喜欢游泳”为事件,然后根据积事件的概率公式可得结果.
【详解】
记“该中学学生喜欢足球”为事件,“该中学学生喜欢游泳”为事件,则“该中学学生喜欢足球或游泳”为事件,“该中学学生既喜欢足球又喜欢游泳”为事件,
则,,,
所以
所以该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例为.
故选:C.
【点睛】
本题考查了积事件的概率公式,属于基础题.
5.(2020·海南·高考真题)我国新冠肺炎疫情进入常态化,各地有序推进复工复产,下面是某地连续11天复工复产指数折线图,下列说法正确的是
A.这11天复工指数和复产指数均逐日增加;
B.这11天期间,复产指数增量大于复工指数的增量;
C.第3天至第11天复工复产指数均超过80%;
D.第9天至第11天复产指数增量大于复工指数的增量;
【答案】CD
【分析】
注意到折线图中有递减部分,可判定A错误;注意考查第1天和第11天的复工复产指数的差的大小,可判定B错误;根据图象,结合复工复产指数的意义和增量的意义可以判定CD正确.
【详解】
由图可知,第1天到第2天复工指数减少,第7天到第8天复工指数减少,第10天到第11复工指数减少,第8天到第9天复产指数减少,故A错误;
由图可知,第一天的复产指标与复工指标的差大于第11天的复产指标与复工指标的差,所以这11天期间,复产指数增量小于复工指数的增量,故B错误;
由图可知,第3天至第11天复工复产指数均超过80%,故C正确;
由图可知,第9天至第11天复产指数增量大于复工指数的增量,故D正确;
【点睛】
本题考查折线图表示的函数的认知与理解,考查理解能力,识图能力,推理能力,难点在于指数增量的理解与观测,属中档题.
6.(2021·全国·高考真题)有一组样本数据,,…,,由这组数据得到新样本数据,,…,,其中(为非零常数,则( )
A.两组样本数据的样本平均数相同
B.两组样本数据的样本中位数相同
C.两组样本数据的样本标准差相同
D.两组样数据的样本极差相同
【答案】CD
【分析】
A、C利用两组数据的线性关系有、,即可判断正误;根据中位数、极差的定义,结合已知线性关系可判断B、D的正误.
【详解】
A:且,故平均数不相同,错误;
B:若第一组中位数为,则第二组的中位数为,显然不相同,错误;
C:,故方差相同,正确;
D:由极差的定义知:若第一组的极差为,则第二组的极差为,故极差相同,正确;
故选:CD
7.(2021·全国·高考真题)下列统计量中,能度量样本的离散程度的是( )
A.样本的标准差 B.样本的中位数
C.样本的极差 D.样本的平均数
【答案】AC
【分析】
考查所给的选项哪些是考查数据的离散程度,哪些是考查数据的集中趋势即可确定正确选项.
【详解】
由标准差的定义可知,标准差考查的是数据的离散程度;
由中位数的定义可知,中位数考查的是数据的集中趋势;
由极差的定义可知,极差考查的是数据的离散程度;
由平均数的定义可知,平均数考查的是数据的集中趋势;
故选:AC.
8.(2020·山东·高考真题)某创新企业为了解新研发的一种产品的销售情况,从编号为001,002,…480的480个专卖店销售数据中,采用系统抽样的方法抽取一个样本,若样本中的个体编号依次为005,021,…则样本中的最后一个个体编号是______.
【答案】469
【分析】
先求得编号间隔为16以及样本容量,再由样本中所有数据编号为求解.
【详解】
间隔为021-005=16,
则样本容量为,
样本中所有数据编号为,
所以样本中的最后一个个体的编号为,
故答案为:469
9.(2021·全国·高考真题(理))某厂研制了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
旧设备 9.8 10.3 10.0 10.2 9.9 9.8 10.0 10.1 10.2 9.7
新设备 10.1 10.4 10.1 10.0 10.1 10.3 10.6 10.5 10.4 10.5
旧设备和新设备生产产品的该项指标的样本平均数分别记为和,样本方差分别记为和.
(1)求,,,;
(2)判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
【答案】(1);(2)新设备生产产品的该项指标的均值较旧设备有显著提高.
【分析】
(1)根据平均数和方差的计算方法,计算出平均数和方差.
(2)根据题目所给判断依据,结合(1)的结论进行判断.
【详解】
(1),
,
,
.
(2)依题意,,,
,所以新设备生产产品的该项指标的均值较旧设备有显著提高.
考点三:计数原理
10.(2020·北京·高考真题)在的展开式中,的系数为( ).
A. B.5 C. D.10
【答案】C
【分析】
首先写出展开式的通项公式,然后结合通项公式确定的系数即可.
【详解】
展开式的通项公式为:,
令可得:,则的系数为:.
故选:C.
【点睛】
二项式定理的核心是通项公式,求解此类问题可以分两步完成:第一步根据所给出的条件(特定项)和通项公式,建立方程来确定指数(求解时要注意二项式系数中n和r的隐含条件,即n,r均为非负整数,且n≥r,如常数项指数为零、有理项指数为整数等);第二步是根据所求的指数,再求所求解的项.
11.(2020·山东·高考真题)在的二项展开式中,第项的二项式系数是( )
A. B. C. D.
【答案】A
【分析】
本题可通过二项式系数的定义得出结果.
【详解】
第项的二项式系数为,
故选:A.
12.(2020·全国·高考真题(理))的展开式中x3y3的系数为( )
A.5 B.10
C.15 D.20
【答案】C
【分析】
求得展开式的通项公式为(且),即可求得与展开式的乘积为或形式,对分别赋值为3,1即可求得的系数,问题得解.
【详解】
展开式的通项公式为(且)
所以的各项与展开式的通项的乘积可表示为:
和
在中,令,可得:,该项中的系数为,
在中,令,可得:,该项中的系数为
所以的系数为
故选:C
【点睛】
本题主要考查了二项式定理及其展开式的通项公式,还考查了赋值法、转化能力及分析能力,属于中档题.
13.(2020·全国·高考真题(理))的展开式中常数项是__________(用数字作答).
【答案】
【分析】
写出二项式展开通项,即可求得常数项.
【详解】
其二项式展开通项:
当,解得
的展开式中常数项是:.
故答案为:.
【点睛】
本题考查二项式定理,利用通项公式求二项展开式中的指定项,解题关键是掌握的展开通项公式,考查了分析能力和计算能力,属于基础题.
14.(2020·天津·高考真题)在的展开式中,的系数是_________.
【答案】10
【分析】
写出二项展开式的通项公式,整理后令的指数为2,即可求出.
【详解】
因为的展开式的通项公式为,令,解得.
所以的系数为.
故答案为:.
【点睛】
本题主要考查二项展开式的通项公式的应用,属于基础题.
15.(2021·浙江·高考真题)已知多项式,则___________,___________.
【答案】; .
【分析】
根据二项展开式定理,分别求出的展开式,即可得出结论.
【详解】
,
,
所以,
,
所以.
故答案为:.
16.(2020·浙江·高考真题)设,则________;________.
【答案】
【分析】
利用二项式展开式的通项公式计算即可.
【详解】
的通项为,
令,则,故;
.
故答案为:;.
【点晴】
本题主要考查利用二项式定理求指定项的系数问题,考查学生的数学运算能力,是一道基础题.
17.(2020·海南·高考真题)6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有( )
A.120种 B.90种
C.60种 D.30种
【答案】C
【分析】
分别安排各场馆的志愿者,利用组合计数和乘法计数原理求解.
【详解】
首先从名同学中选名去甲场馆,方法数有;
然后从其余名同学中选名去乙场馆,方法数有;
最后剩下的名同学去丙场馆.
故不同的安排方法共有种.
故选:C
【点睛】
本小题主要考查分步计数原理和组合数的计算,属于基础题.
18.(2020·海南·高考真题)要安排3名学生到2个乡村做志愿者,每名学生只能选择去一个村,每个村里至少有一名志愿者,则不同的安排方法共有( )
A.2种 B.3种 C.6种 D.8种
【答案】C
【分析】
首先将3名学生分成两个组,然后将2组学生安排到2个村即可.
【详解】
第一步,将3名学生分成两个组,有种分法
第二步,将2组学生安排到2个村,有种安排方法
所以,不同的安排方法共有种
故选:C
【点睛】
解答本类问题时一般采取先组后排的策略.
19.(2021·全国·高考真题(理))将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有( )
A.60种 B.120种 C.240种 D.480种
【答案】C
【分析】
先确定有一个项目中分配2名志愿者,其余各项目中分配1名志愿者,然后利用组合,排列,乘法原理求得.
【详解】
根据题意,有一个项目中分配2名志愿者,其余各项目中分配1名志愿者,可以先从5名志愿者中任选2人,组成一个小组,有种选法;然后连同其余三人,看成四个元素,四个项目看成四个不同的位置,四个不同的元素在四个不同的位置的排列方法数有4!种,根据乘法原理,完成这件事,共有种不同的分配方案,
故选:C.
【点睛】
本题考查排列组合的应用问题,属基础题,关键是首先确定人数的分配情况,然后利用先选后排思想求解.
20.(2020·山东·高考真题)现从4名男生和3名女生中,任选3名男生和2名女生,分别担任5门不同学科的课代表,则不同安排方法的种数是( )
A.12 B.120 C.1440 D.17280
【答案】C
【分析】
首先选3名男生和2名女生,再全排列,共有种不同安排方法.
【详解】
首先从4名男生和3名女生中,任选3名男生和2名女生,共有种情况,
再分别担任5门不同学科的课代表,共有种情况.
所以共有种不同安排方法.
故选:C
21.(2020·全国·高考真题(理))4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学,则不同的安排方法共有__________种.
【答案】
【分析】
根据题意,有且只有2名同学在同一个小区,利用先选后排的思想,结合排列组合和乘法计数原理得解.
【详解】
4名同学到3个小区参加垃圾分类宣传活动,每名同学只去1个小区,每个小区至少安排1名同学
先取2名同学看作一组,选法有:
现在可看成是3组同学分配到3个小区,分法有:
根据分步乘法原理,可得不同的安排方法种
故答案为:.
【点睛】
本题主要考查了计数原理的综合应用,解题关键是掌握分步乘法原理和捆绑法的使用,考查了分析能力和计算能力,属于中档题.
试卷第2页,共2页
同课章节目录
