河南省漯河市临颍县第一高中2021-2022学年高二11月月考数学试卷(Word版含答案)
文档属性
| 名称 | 河南省漯河市临颍县第一高中2021-2022学年高二11月月考数学试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 402.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 08:18:19 | ||
图片预览


文档简介
临颍县第一高中2021-2022学年高二11月月考
数学试卷
一、单选题
1.已知全集U={1,2,3,4,5},集合M={1,2},N={3,4},则Cu(MUN)=( )
A. {5} B. {1,2} C. {3,4} D. {1,2,3,4}
2.若随机变量X的分布列如表,则 的值为( )
1 2 3
A. B. 1 C. D.
3.在 内,不等式 的解集是( )
A. B. C. D.
4.已知命题 ,则 为( )
A. B. C. D.
5.2019年9月1日兰州地铁一号线正式开通,两位同学同时去乘坐地铁,一列地铁有 节车厢,两人进入车厢的方法数共有( )
A. 15种 B. 30种 C. 36种 D. 64种
6.圆锥的高为1,体积为 ,则过该圆锥顶点的平面截此圆锥所得截面面积的最大值为( )
A.2
B.
C.
D.1
7.在平面四边形 中, ,若 ,则向量 与 夹角的余弦值为( )
A. B. C. D.
8.无论 取何实数,直线 恒过一定点,则该定点坐标为( )
A.
B.
C.
D.
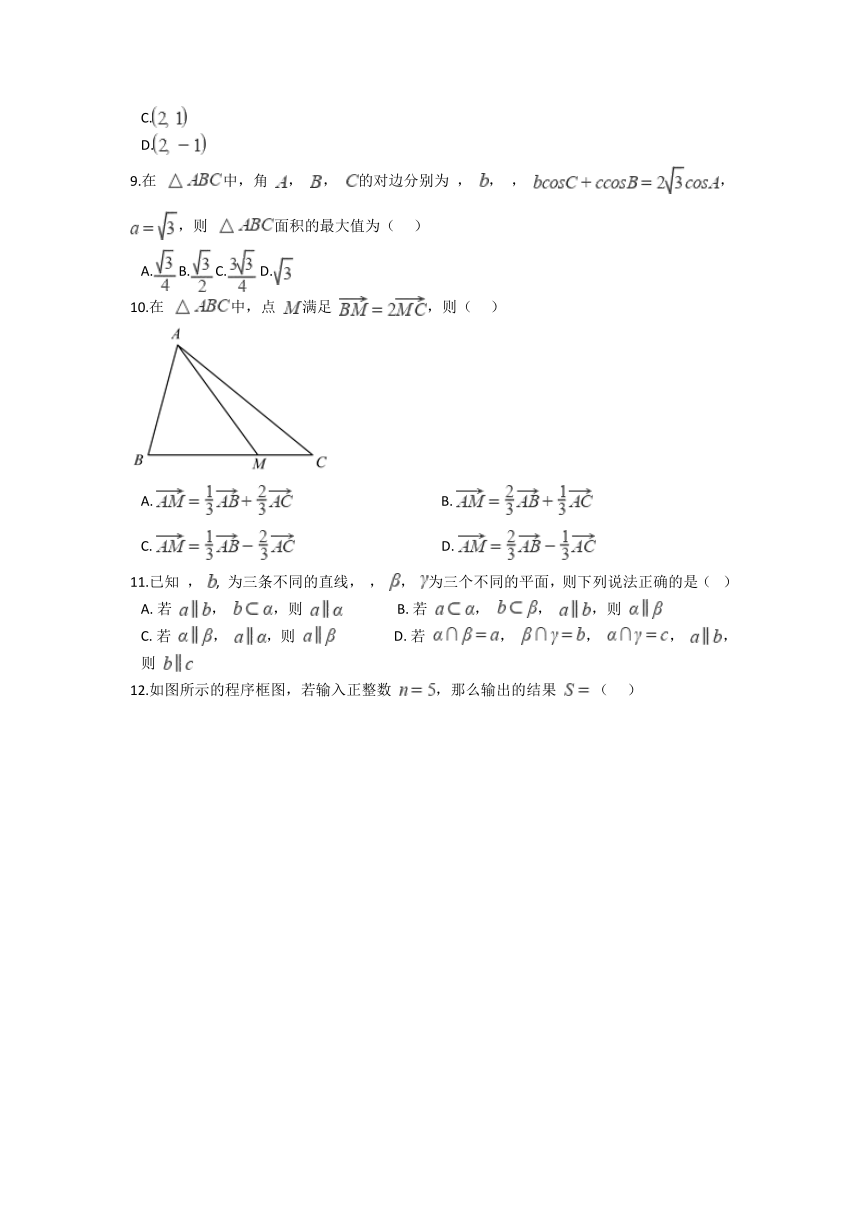
9.在 中,角 , , 的对边分别为 , , , , ,则 面积的最大值为( )
A.B.C.D.
10.在 中,点 满足 ,则( )
A. B.
C. D.
11.已知 , , 为三条不同的直线, , , 为三个不同的平面,则下列说法正确的是( )
A. 若 , ,则 B. 若 , , ,则
C. 若 , ,则 D. 若 , , , ,则
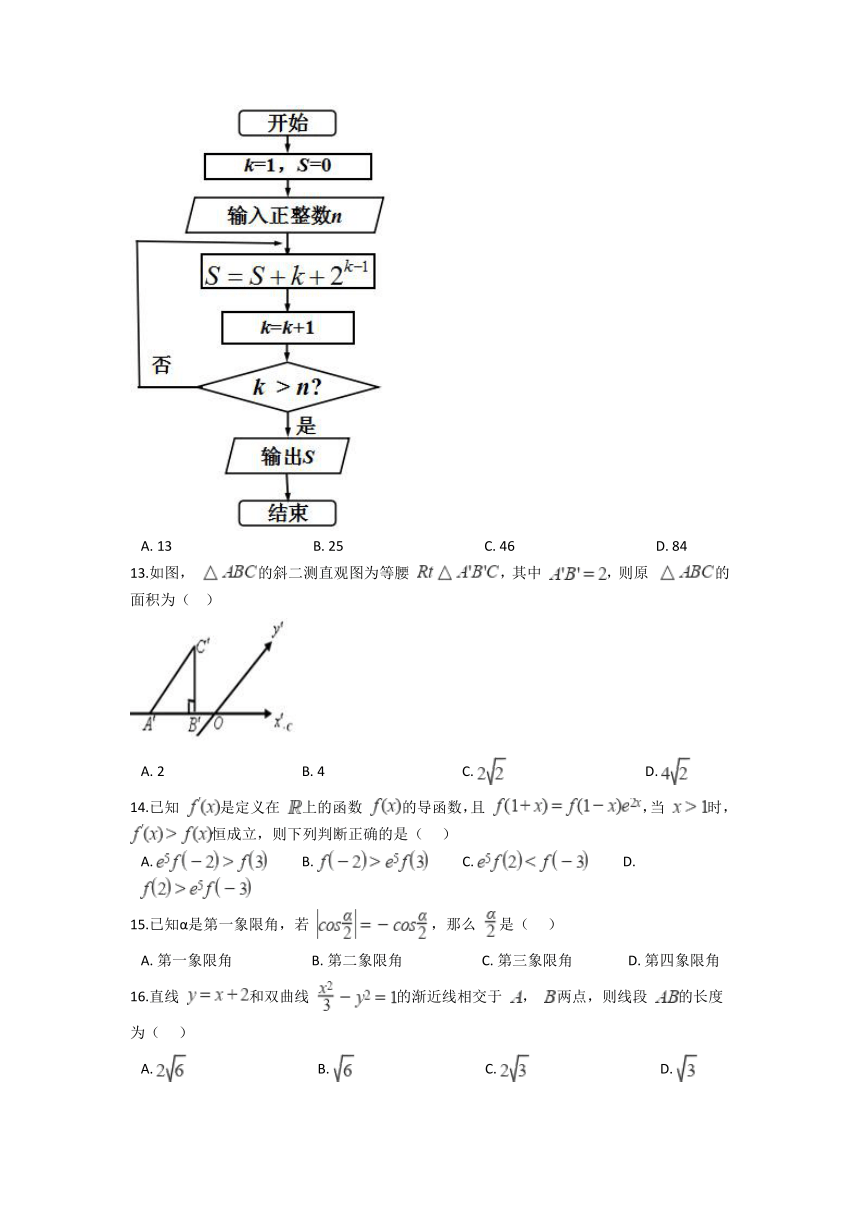
12.如图所示的程序框图,若输入正整数 ,那么输出的结果 ( )
A. 13 B. 25 C. 46 D. 84
13.如图, 的斜二测直观图为等腰 ,其中 ,则原 的面积为( )
A. 2 B. 4 C. D.
14.已知 是定义在 上的函数 的导函数,且 ,当 时, 恒成立,则下列判断正确的是( )
A. B. C. D.
15.已知α是第一象限角,若 ,那么 是( )
A. 第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
16.直线 和双曲线 的渐近线相交于 , 两点,则线段 的长度为( )
A. B. C. D.
17.下列函数中与函数 值域相同的是( )
A. B. C. D.
18.要得到函数 的图像,只需将函数 的图像( )
A. 向左平移 个单位 B. 向右平移 个单位 C. 向左平移 个单位 D. 向右平移 个单位
19.已知 ,则( )
A. B. C. D.
20.已知双曲线C: ( , )的左、右焦点分别为 , ,点P是C的右支上一点,连接 与y轴交于点M,若 (O为坐标原点), ,则双曲线C的离心率为( )
A. B. 2 C. D. 3
二、填空题
21.如图,正方体 中,E,F,M,N分别为 的中点,则直线 , 所成角的大小为________.
22.在平面直角坐标系中,O为坐标原点,且满足 = + ,则 =________.
23.已知 ,则函数 的最小值为 .
24.在 中, , ,且 , ,其中 ,且 ,若 , 分别为线段 , 中点,当线段 取最小值时 ________.
25.已知函数 有且只有一个零点,则 的取值范围是 .
26.在平行四边形ABCD中, =e1 , =e2 , = , = ,则 = (用e1 , e2表示).
27.若 则 的取值范围是________.
三、解答题
28.设集合 , ,若 ,
(1)求集合A;
(2)求实数a的取值范围.
29.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=2,cosB= .
(1)若b=3,求sinA的值;
(2)若△ABC的面积S△ABC=3,求b,c的值.
30.一机构随机调查了某小区100人的月收入情况,将所得数据按 , , , , , (单位:元)分成六组,并且作出如图所示的频率分布直方图.
(1)根据频率分布直方图估计样本数据的中位数;
(2)根据题目分组情况,按分层抽样的方法在 , , 三组中抽取6人,再从这6人中抽取2人,求至少有一人收入在 的概率.
31.设全集 ,集合
(1)求 ;
(2)若集合 ,且 ,求实数 的取值范围;
(3)若集合 ,且 ,求实数 的取值范围.
32.已知函数 , .
(1)证明: 的唯一的零点在 内;
(2)若对任意的 , , 恒成立,求 的取值范围.
答案部分
一、单选题
1.【答案】 A
2.【答案】 D
3.【答案】 C
4.【答案】 A
5.【答案】 C
6.【答案】 A
7.【答案】 D
8.【答案】 A
9.【答案】 C
10.【答案】 A
11.【答案】 D
12.【答案】 C
13.【答案】 D
14.【答案】 A
15.【答案】 C
16.【答案】 A
17.【答案】 D
18.【答案】 A
19.【答案】 D
20.【答案】 C
二、填空题
21.【答案】
22.【答案】
23.【答案】 3
24.【答案】
25.【答案】
26.【答案】 - e1+ e2
27.【答案】
三、解答题
28.【答案】 (1)因为 ,所以 ,
所以 ,
故 ;
(2)因为 ,所以 ,
不等式 等价于 ,
当 时, ,
因为 ,所以 ,解得 ;
当 时,则 ,不满足 ;
当 时,则 ,满足 ;
综上,a的取值范围是: .
29.【答案】 (1)解:因为 ,
所以 .
由正弦定理,得
(2)解:因为 ,
所以 .
由余弦定理,得 .
所以
30.【答案】 (1)解:设数据在 内的概率为m,由频率分布直方图得,
易知中位数在 ,
设中位数为 ,则 ,
解得 .
(2)解:收入在 , , 这三组的人数分别为10,15,5,
所以按分层抽样的方法在各组抽取的人数分别2,3,1.
记收入在 的2人分别为 , ,收入在 的3人分别为 , , ,收入在 的1人为 ,
通过列举法可得从这6人中抽取2人的取法有 , , , , , , , , , , , , , , ,共15种,
其中至少有一人收入在 的取法有 , , , , , , , , , , , ,共12种,
所以至少有一人收在 概率为 .
31.【答案】 (1)解: ,
故 .
(2)解: ,因为 ,故 即 .
(3)解:因为 ,所以 即 .
32.【答案】 (1)解: , , 函数 在 内存在零点.
因为函数 在 上为增函数,故函数 的唯一的零点在 内
(2)解: 函数 在 上为增函数,
函数 在 上的最小值为 .
, .
当 时,函数 在 上的最大值为 ,则 ,解得 ;
当 时,函数 在 上的最大值为 ,
则 ,解得 ,又 ,不合题意.
综上, 的取值范围为 .
数学试卷
一、单选题
1.已知全集U={1,2,3,4,5},集合M={1,2},N={3,4},则Cu(MUN)=( )
A. {5} B. {1,2} C. {3,4} D. {1,2,3,4}
2.若随机变量X的分布列如表,则 的值为( )
1 2 3
A. B. 1 C. D.
3.在 内,不等式 的解集是( )
A. B. C. D.
4.已知命题 ,则 为( )
A. B. C. D.
5.2019年9月1日兰州地铁一号线正式开通,两位同学同时去乘坐地铁,一列地铁有 节车厢,两人进入车厢的方法数共有( )
A. 15种 B. 30种 C. 36种 D. 64种
6.圆锥的高为1,体积为 ,则过该圆锥顶点的平面截此圆锥所得截面面积的最大值为( )
A.2
B.
C.
D.1
7.在平面四边形 中, ,若 ,则向量 与 夹角的余弦值为( )
A. B. C. D.
8.无论 取何实数,直线 恒过一定点,则该定点坐标为( )
A.
B.
C.
D.
9.在 中,角 , , 的对边分别为 , , , , ,则 面积的最大值为( )
A.B.C.D.
10.在 中,点 满足 ,则( )
A. B.
C. D.
11.已知 , , 为三条不同的直线, , , 为三个不同的平面,则下列说法正确的是( )
A. 若 , ,则 B. 若 , , ,则
C. 若 , ,则 D. 若 , , , ,则
12.如图所示的程序框图,若输入正整数 ,那么输出的结果 ( )
A. 13 B. 25 C. 46 D. 84
13.如图, 的斜二测直观图为等腰 ,其中 ,则原 的面积为( )
A. 2 B. 4 C. D.
14.已知 是定义在 上的函数 的导函数,且 ,当 时, 恒成立,则下列判断正确的是( )
A. B. C. D.
15.已知α是第一象限角,若 ,那么 是( )
A. 第一象限角 B. 第二象限角 C. 第三象限角 D. 第四象限角
16.直线 和双曲线 的渐近线相交于 , 两点,则线段 的长度为( )
A. B. C. D.
17.下列函数中与函数 值域相同的是( )
A. B. C. D.
18.要得到函数 的图像,只需将函数 的图像( )
A. 向左平移 个单位 B. 向右平移 个单位 C. 向左平移 个单位 D. 向右平移 个单位
19.已知 ,则( )
A. B. C. D.
20.已知双曲线C: ( , )的左、右焦点分别为 , ,点P是C的右支上一点,连接 与y轴交于点M,若 (O为坐标原点), ,则双曲线C的离心率为( )
A. B. 2 C. D. 3
二、填空题
21.如图,正方体 中,E,F,M,N分别为 的中点,则直线 , 所成角的大小为________.
22.在平面直角坐标系中,O为坐标原点,且满足 = + ,则 =________.
23.已知 ,则函数 的最小值为 .
24.在 中, , ,且 , ,其中 ,且 ,若 , 分别为线段 , 中点,当线段 取最小值时 ________.
25.已知函数 有且只有一个零点,则 的取值范围是 .
26.在平行四边形ABCD中, =e1 , =e2 , = , = ,则 = (用e1 , e2表示).
27.若 则 的取值范围是________.
三、解答题
28.设集合 , ,若 ,
(1)求集合A;
(2)求实数a的取值范围.
29.在△ABC中,角A,B,C所对的边分别为a,b,c,且a=2,cosB= .
(1)若b=3,求sinA的值;
(2)若△ABC的面积S△ABC=3,求b,c的值.
30.一机构随机调查了某小区100人的月收入情况,将所得数据按 , , , , , (单位:元)分成六组,并且作出如图所示的频率分布直方图.
(1)根据频率分布直方图估计样本数据的中位数;
(2)根据题目分组情况,按分层抽样的方法在 , , 三组中抽取6人,再从这6人中抽取2人,求至少有一人收入在 的概率.
31.设全集 ,集合
(1)求 ;
(2)若集合 ,且 ,求实数 的取值范围;
(3)若集合 ,且 ,求实数 的取值范围.
32.已知函数 , .
(1)证明: 的唯一的零点在 内;
(2)若对任意的 , , 恒成立,求 的取值范围.
答案部分
一、单选题
1.【答案】 A
2.【答案】 D
3.【答案】 C
4.【答案】 A
5.【答案】 C
6.【答案】 A
7.【答案】 D
8.【答案】 A
9.【答案】 C
10.【答案】 A
11.【答案】 D
12.【答案】 C
13.【答案】 D
14.【答案】 A
15.【答案】 C
16.【答案】 A
17.【答案】 D
18.【答案】 A
19.【答案】 D
20.【答案】 C
二、填空题
21.【答案】
22.【答案】
23.【答案】 3
24.【答案】
25.【答案】
26.【答案】 - e1+ e2
27.【答案】
三、解答题
28.【答案】 (1)因为 ,所以 ,
所以 ,
故 ;
(2)因为 ,所以 ,
不等式 等价于 ,
当 时, ,
因为 ,所以 ,解得 ;
当 时,则 ,不满足 ;
当 时,则 ,满足 ;
综上,a的取值范围是: .
29.【答案】 (1)解:因为 ,
所以 .
由正弦定理,得
(2)解:因为 ,
所以 .
由余弦定理,得 .
所以
30.【答案】 (1)解:设数据在 内的概率为m,由频率分布直方图得,
易知中位数在 ,
设中位数为 ,则 ,
解得 .
(2)解:收入在 , , 这三组的人数分别为10,15,5,
所以按分层抽样的方法在各组抽取的人数分别2,3,1.
记收入在 的2人分别为 , ,收入在 的3人分别为 , , ,收入在 的1人为 ,
通过列举法可得从这6人中抽取2人的取法有 , , , , , , , , , , , , , , ,共15种,
其中至少有一人收入在 的取法有 , , , , , , , , , , , ,共12种,
所以至少有一人收在 概率为 .
31.【答案】 (1)解: ,
故 .
(2)解: ,因为 ,故 即 .
(3)解:因为 ,所以 即 .
32.【答案】 (1)解: , , 函数 在 内存在零点.
因为函数 在 上为增函数,故函数 的唯一的零点在 内
(2)解: 函数 在 上为增函数,
函数 在 上的最小值为 .
, .
当 时,函数 在 上的最大值为 ,则 ,解得 ;
当 时,函数 在 上的最大值为 ,
则 ,解得 ,又 ,不合题意.
综上, 的取值范围为 .
同课章节目录
