2021年全国甲卷高考数学(理科)真题变式汇编(含解析)
文档属性
| 名称 | 2021年全国甲卷高考数学(理科)真题变式汇编(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 11:44:36 | ||
图片预览




文档简介
变式题库
【原卷 1 题】 知识点 并集,交集
【正确答案】 B
【试题解析】
1-1【基础】 已知集合M={x|﹣4<x≤2},N={x|y=},则M∩N=( )
A.{2} B.{x|﹣4<x≤﹣2}
C.{x|﹣4<x≤2} D.{x|﹣2≤x≤2}
【正确答案】 B
1-2【巩固】 设集合,,则( )
A. B. C. D.
【正确答案】 A
1-3【巩固】 已知集合P={x∈N|x≤3},Q={x|x2≤x+2},则P∩Q=( )
A.{﹣1,0,1,2} B.[0,2] C.{0,1,2} D.{1,2}
【正确答案】 C
1-4【基础】 设集合,集合,则集合=
A. B. C. D.
【正确答案】 A
1-5【提升】 已知集合,,则( )
A. B. C. D.
【正确答案】 A
1-6【提升】 集合,,求( )
A. B. C. D.
【正确答案】 A
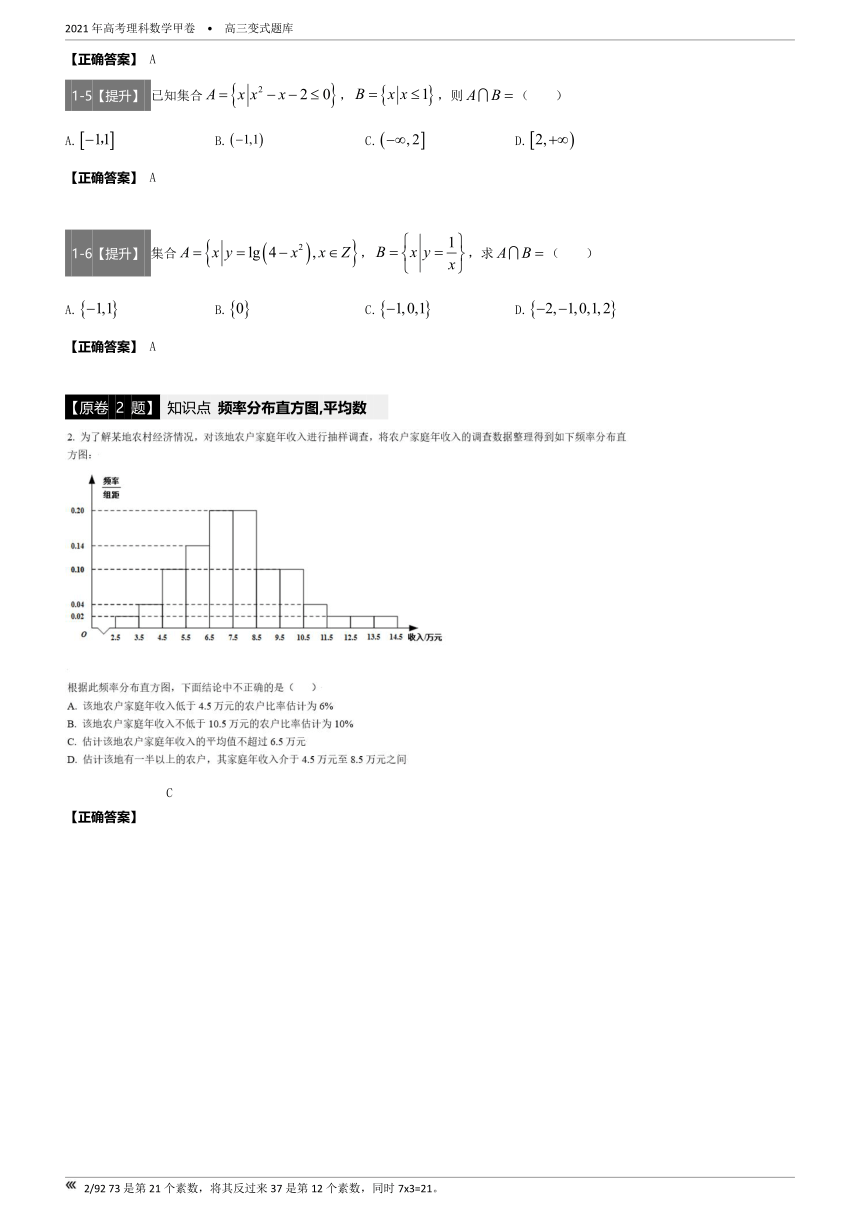
【原卷 2 题】 知识点 频率分布直方图,平均数
【正确答案】 C
【试题解析】
2-1【基础】 爱美之心,人皆有之.健身减肥已成为很多肥胖者业余选择的项目.为了了解运动健身减肥的效果,某健身房调查了40名肥胖者,健身之前他们的体重(单位:)情况如柱状图1所示,经过四个月的健身后,他们的体重情况如柱状图2所示.对比健身前后,关于这40名肥胖者,下面结论不正确的是( )
A.他们健身后,体重在区间内的人数增加了4个
B.他们健身后,体重在区间内的人数没有改变
C.因为体重在内所占比例没有发生变化,所以说明健身对体重没有任何影响
D.他们健身后,原来体重在区间内的肥胖者体重都有减少
【正确答案】 C
2-2【巩固】 供电部门对某社区1000位居民2019年4月份人均用电情况进行统计后,按人均用电量分为,,,五组,整理得到如下的频率分布直方图,则下列说法错误的是
A.4月份人均用电量人数最多的一组有400人
B.4月份人均用电量不低于20度的有500人
C.4月份人均用电量为25度
D.在这1000位居民中任选1位协助收费,选到的居民用电量在一组的概率为
【正确答案】 C
2-3【提升】 下面是追踪调查200个某种电子元件寿命(单位:)频率分布直方图,如图:
其中300-400、400-500两组数据丢失,下面四个说法中有且只有一个与原数据相符,这个说法是
①寿命在300-400的频数是90;
②寿命在400-500的矩形的面积是0.2;
③用频率分布直方图估计电子元件的平均寿命为:
④寿命超过的频率为0.3
A.① B.② C.③ D.④
【正确答案】 B
2-4【巩固】 在2019年某省普通高中学业水平考试(合格考)中,对全省所有考生的物成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为,,,,,90分以上为优秀,则下列说法中不正确的是( )
A.从全体考生中随机抽取1000人,则其中得优秀考试约有100人
B.若要全省的合格考通过率达到,则合格分数线约为44分
C.若同一组中数据用该组区间中间值作代表值,可得考试物理成绩的平均分约为70
D.该省考生物理成绩的中位数为75分
【正确答案】 D
2-5【提升】 2021年4月8日,教育部办公厅“关于进一步加强中小学生体质健康管理工作的通知”中指出,各地要加强对学生体质健康重要性的宣传,中小学校要通过体育与健康课程、大课间、课外体育锻炼、体育竞赛、班团队活动、家校协同联动等多种形式加强教育引导,让家长和中小学生科学认识体质健康的影响因素.了解运动在增强体质、促进健康、预防肥胖与近视、锤炼意志、健全人格等方面的重要作用,提高学生体育与健康素养.增强体质健康管理的意识和能力.某高中学校共有2000名男生,为了了解这部分学生的身体发育情况,学校抽查了100 名男生的体重情况.根据所得数据绘制样本的频率分布直方图如图所示.根据此图,下列说法中错误的是( )
A.样本的众数约为
B.样本的中位数约为
C.样本的平均值约为66
D.为确保学生体质健康,学校将对体重超过的学生进行健康监测,该校男生中需要监测的学生频数约为200人
【正确答案】 C
2-6【基础】 某校为了解学生体能素质,随机抽取了50名学生,进行体能测试,并将这50名学生成绩整理得如下频率分布直方图.根据此频率分布直方图,下列结论中不正确的是( )
A.这50名学生中成绩在[80,100]内的人数有10人
B.这50名学生中成绩在[40,60)内的人数占比为28%
C.这50名学生成绩的中位数为70
D.这50名学生的平均成绩(同一组中的数据用该组区间的中点值做代表)
【正确答案】 C
【原卷 3 题】 知识点 复数的乘除和乘方
【正确答案】 B
【试题解析】
3-1【提升】 若,则( )
A.0 B.1
C. D.2
【正确答案】 C
3-2【基础】 若复数满足,其中是虚数单位,则( )
A. B. C. D.
【正确答案】 A
3-3【提升】 已知复数满足,则( )
A. B. C. D.
【正确答案】 A
3-4【基础】 已知复数满足,则( )
A. B. C. D.
【正确答案】 B
3-5【巩固】 在复平面内,复数满足,则( )
A. B. C. D.
【正确答案】 D
3-6【巩固】 设,则( )
A. B. C. D.
【正确答案】 A
【原卷 4 题】 知识点 对数的运算,对数函数的概念,对数的概念
【正确答案】 C
【试题解析】
4-1【基础】 某科技股份有限公司为激励创新,计划逐年增加研发资金投入.若该公司2020年全年投入的研发资金为100万元,在此基础上,每年投入的研发资金比上一年增长,则该公司全年投入的研发资金开始超过140万元的年份是参考数据:,( )
A.2025年 B.2026年 C.2027年 D.2028年
【正确答案】 B
4-2【巩固】 声强级(单位:)由公式给出,其中为声强(单位:).某班级为规范同学在公共场所说话的文明礼仪,开展了“不敢高声语,恐惊读书人”主题活动,要求课下同学之间交流时,每人的声强级不超过40.现有4位同学课间交流时,声强分别为,,,,则这4人中达到班级要求的有( )
A.1人 B.2人 C.3人 D.4人
【正确答案】 C
4-3【基础】 某工厂产生的废气必须经过过滤后排放,规定排放时污染物的残留含量不得超过原污染物总量的0.5%.已知在过滤过程中的污染物的残留数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为(为原污染物总量).要能够按规定排放废气,则需要过滤n小时,则正整数n的最小值为(参考数据:取)( )
A.13 B.14 C.15 D.16
【正确答案】 D
4-4【提升】 为了保证信息安全传输,有一种称为秘密密钥密码系统,其加密 解密原理如图:,现在加密密钥为,解密密钥为,如下所示:发送方发送明文“1”,通过加密后得到密文“18”,再发送密文“18”,接受方通过解密密钥解密得明文“49”,问若接受方接到明文“4”,则发送方发送明文为( )
A. B. C.162 D.
【正确答案】 A
4-5【巩固】 我们知道:人们对声音有不同的感觉,这与它的强度有关系.一般的,声音的强度用()表示,但在实际测量时,声音的强度水平常用(单位:分贝,,其中是人们平均能听到的最小强度,是听觉的开端).某新建的小区规定:小区内公共场所的声音的强度水平必须保持在50分贝以下,则声音强度的取值范围是( )
A. B. C. D.
【正确答案】 C
4-6【提升】 香农定理是所有通信制式最基本的原理,它可以用香农公式来表示,其中是信道支持的最大速度或者叫信道容量,是信道的带宽(),S是平均信号功率(),是平均噪声功率().已知平均信号功率为,平均噪声功率为,在不改变平均信号功率和信道带宽的前提下,要使信道容量增大到原来的2倍,则平均噪声功率约降为( )
A. B. C. D.
【正确答案】 A
【原卷 5 题】 知识点 双曲线的定义,双曲线的离心率,余弦定理
【正确答案】 A
【试题解析】
5-1【提升】 分别是双曲线的左、右焦点,过的直线分别交该双曲线的左、右两支于A、B两点,若,则( )
A.2 B. C.4 D.
【正确答案】 C
5-2【提升】 已知双曲线(,)的左右焦点,,过的直线交右支于、两点,若,,则该双曲线的离心率为( )
A. B.2 C. D.
【正确答案】 B
5-3【巩固】 已知分别是双曲线的两个焦点,双曲线和圆的一个交点为,且,那么双曲线的离心率为( )
A. B. C.2 D.
【正确答案】 D
5-4【巩固】 设为双曲线:的左焦点,为坐标原点,以为圆心,为半径的圆与交于两点.若,则的离心率为( )
A. B. C. D.
【正确答案】 A
5-5【基础】 已知双曲线与函数的图象交于点,若函数的图象在点处的切线过双曲线左焦点,则双曲线的离心率是( )
A. B. C. D.
【正确答案】 D
5-6【基础】 已知双曲线:的左、右焦点分别为,,点在的右支上,直线与的左支交于点,若,且,则的离心率为( )
A. B. C. D.
【正确答案】 D
【原卷 6 题】 知识点 画几何体的三视图,三视图
【正确答案】 D
【试题解析】
6-1【巩固】 在空间直角坐标系中,一个四面体的顶点坐标分别为,,,.画该四面体三视图中的正视图时,以平面为投影面,则得到正视图可以为( ).
A. B. C. D.
【正确答案】 A
6-2【基础】 一个锥体的正视图和侧视图如图所示,下面选项中,不可能是该锥体的俯视图的是
A. B. C. D.
【正确答案】 C
6-3【提升】 将正三棱柱截去三个角(如图1所示A,B,C分别是△CHI三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为
A. B. C. D.
【正确答案】 A
6-4【提升】 如图所示的几何体各自的三视图中,有且仅有两个视图相同的为
A.①② B.②④
C.①④ D.①③
【正确答案】 B
6-5【基础】 在如图所示的空间直角坐标系中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为
A.①和② B.③和① C.④和③ D.④和②
【正确答案】 D
6-6【巩固】 如下图,在正方体中,点是棱上一点,则三棱锥的侧视图是
A. B. C. D.
【正确答案】 D
【原卷 7 题】 知识点 必要不充分条件,递增数列与递减数列
【正确答案】 B
【试题解析】
7-1【提升】 设无穷等比数列{an}的前n项和为Sn若-a1<a2<a1,则( )
A.{Sn}为递减数列 B.{Sn}为递增数列
C.数列{Sn}有最大项 D.数列{Sn}有最小项
【正确答案】 D
7-2【巩固】 已知数列{an}满足a1=2,2anan+1= +1,设bn=,则数列{bn}是( )
A.常数列 B.摆动数列
C.递增数列 D.递减数列
【正确答案】 D
7-3【巩固】 已知数列满足,其中且,则下列说法正确的是( )
A.当时,存在一个实数和正整数,使得,,成等差数列
B.当时,存在一个实数和正整数,使得,,成等差数列
C.当时,数列是递增的
D.当时,数列是递减的
【正确答案】 D
7-4【提升】 已知数列满足,,则下列选项中正确的是( )
A. A当且仅当时,数列为递增数列
B. B.存在实数和正整数,,使得
C. C.当且仅当时,数列为递减数列
D. D当时,数列,均为递增数列
【正确答案】 D
7-5【基础】 已知数列的项都是实数,则对于一切,“数列为递减数列”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.不充分也不必要条件
【正确答案】 B
7-6【基础】 在等比数列{an}中,“a2>a1”是“{an}为递增数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要
【正确答案】 B
【原卷 8 题】 知识点 两角和与差的正弦公式,正弦定理
【正确答案】 B
【试题解析】
8-1【基础】 雕塑成了大学环境不可分割的一部分,有些甚至能成为这个大学的象征,在中国科学技术大学校园中就有一座郭沫若的雕像.雕像由像体和底座两部分组成.如图,在中,,在中,,且米,求像体的高度( )(最后结果精确到0.1米,参考数据:,,)
A.4.0米 B.4.2米 C.4.3米 D.4.4米
【正确答案】 B
8-2【基础】 为了测量西藏被誉称为“阿里之巅”冈仁波齐山峰的高度,通常采用人工攀登的方式进行,测量人员从山脚开始,直到到达山顶分段测量,最后将所有的高度差累加,得到珠峰的高度,在测量过程中,已知竖立在点处的测量觇标高米,攀登者们在处测得到觇标底点和顶点的仰角分别为,,则、的高度差约为( )
(参考数据:,,)
A.米 B.米
C.米 D.米
【正确答案】 C
8-3【巩固】 “欲穷千里目,更上一层楼”出自唐朝诗人王之涣的《登鹳雀楼》,鹳雀楼位于今山西永济市,该楼有三层,前对中条山,下临黄河,传说常有鹳雀在此停留,故有此名.下面是复建的鹳雀楼的示意图,某位游客(身高忽略不计)从地面点看楼顶点的仰角为30°,沿直线前进79米到达点,此时看点的仰角为45°,若,则楼高约为( ).
A.65米 B.74米 C.83米 D.92米
【正确答案】 B
8-4【巩固】 圣·索菲亚教堂(英语:SAINT SOPHIA CATHEDRAL)坐落于中国黑龙江省,是一座始建于1907年拜占庭风格的东正教教堂,距今已有114年的历史,为哈尔滨的标志性建筑.1996年经国务院批准,被列为第四批全国重点文物保护单位,是每一位到哈尔滨旅游的游客拍照打卡的必到景点其中央主体建筑集球,圆柱,棱柱于一体,极具对称之美,可以让游客从任何角度都能领略它的美.小明同学为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物,高为,在它们之间的地面上的点(三点共线)处测得楼顶,教堂顶的仰角分别是和,在楼顶处测得塔顶的仰角为,则小明估算索菲亚教堂的高度为( )
A. B. C. D.
【正确答案】 D
8-5【提升】 魏晋时刘徽撰写的《海岛算经》是有关测量的数学著作,其中第一题是测海岛的高.如图,点,,在水平线上,和是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,称为“表距”,和都称为“表目距”,与的差称为“表目距的差”则海岛的高( )
A.表高 B.表高
C.表距 D.表距
【正确答案】 A
8-6【提升】 如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°,从C点测得∠MCA=60°,已知山高BC=100 m,则山高MN=( )
A.150m B.180m C.120m D.160m
【正确答案】 A
【原卷 9 题】 知识点 已知正(余)弦求余(正)弦,由条件等式求正、余弦,已知弦(切)求切(弦),同角三角函数的基本关系,二倍角的正弦公式,二倍角的余弦公式
【正确答案】 A
【试题解析】
9-1【巩固】 已知,(0, π),则=
A.1 B. C. D.1
【正确答案】 A
9-2【提升】 已知,则( )
A. B. C. D.
【正确答案】 C
9-3【基础】 已知,,则( )
A. B. C. D.
【正确答案】 D
9-4【巩固】 若,是第三象限角,则( )
A. B. C. D.
【正确答案】 A
9-5【提升】 若,则( )
A. B. C. D.
【正确答案】 C
9-6【基础】 已知,且,则
A.2 B. C.3 D.
【正确答案】 A
【原卷 10 题】 知识点 排列应用题,古典概型的概率计算公式
【正确答案】 C
【试题解析】
10-1【基础】 从包括甲 乙在内的7名学生中选派4名学生排序参加演讲比赛,则甲和乙参加,且演讲顺序不相邻的概率为( )
A. B. C. D.
【正确答案】 B
10-2【提升】 从分别写有的张卡片中随机抽取张,放回后再随机抽取张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
A. B. C. D.
【正确答案】 D
10-3【基础】 生物实验室有5只兔子,其中只有3只测量过某项指标,若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为
A. B. C. D.
【正确答案】 B
10-4【提升】 如图为我国数学家赵爽约3世纪初在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则区域涂色不相同的概率为
A. B. C. D.
【正确答案】 D
10-5【基础】 我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“— —”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是
A. B. C. D.
【正确答案】 A
10-6【基础】 6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有( )
A.120种 B.90种
C.60种 D.30种
【正确答案】 C
【原卷 11 题】 知识点 球,柱、锥、台的体积,组合体的表面积和体积
【正确答案】 A
【试题解析】
11-1【巩固】 已知矩形的顶点都在半径为5的球的球面上,且,,则棱锥的体积为( )
A. B. C. D.
【正确答案】 C
11-2【基础】 已知,,三点均在球的表面上,,且球心到平面的距离为2,则球的内接正方体的棱长为( )
A.1 B. C.2 D.
【正确答案】 D
11-3【提升】 已知在中,角所对的边分别为,且又点都在球的球面上,且点到平面的距离为,则球的体积为( )
A. B. C. D.
【正确答案】 C
11-4【巩固】 一个球面上有三个点、、,若,,球心到平面的距离为1,则球的表面积为( )
A. B. C. D.
【正确答案】 D
11-5【提升】 已知是面积为的等边三角形,且其顶点都在球的球面上,若球的体积为,则到平面的距离为( )
A. B. C.1 D.
【正确答案】 C
11-6【基础】 平面截球所得截面圆的面积为,球心到平面的距离为,则此球的表面积为( )
A. B. C. D.
【正确答案】 D
【原卷 12 题】 知识点 函数的奇偶性,函数的周期性
【正确答案】 D
【试题解析】
12-1【巩固】 已知函数在定义域上单调,且,则的值为( )
A.3 B.1 C.0 D.﹣1
【正确答案】 A
12-2【基础】 已知函数是R上的偶函数.若对于都有,且当时,,则的值为( )
A.﹣2 B.﹣1 C.1 D.2
【正确答案】 C
12-3【巩固】 函数是上的奇函数,满足,当时,有,求的值( )
A.0 B.1 C. D.
【正确答案】 A
12-4【基础】 已知函数是定义域为R的奇函数,周期为2,且当时,,则 等于( )
A. B. C. D.
【正确答案】 B
12-5【提升】 已知函数满足,若在上为偶函数,且其解析式为,则的值为
A. 1 B.0
C. D.
【正确答案】 B
12-6【提升】 已知函数的定义域为,且函数的图象关于轴对称,函数的图象关于原点对称,则
A. B. C. D.
【正确答案】 A
【原卷 13 题】 知识点 导数的几何意义
【正确答案】 5x-y+2=0
【试题解析】
13-1【提升】 曲线在点处的切线与两坐标轴所围成的三角形的面积为_______.
【正确答案】
13-2【基础】 曲线在点处的切线的横纵截距之和为__________.
【正确答案】
13-3【巩固】 在平面直角坐标系中,曲线在处的切线方程是___________.
【正确答案】
13-4【提升】 已知为奇函数,当时,,则曲线在处的切线方程是_________.
【正确答案】
13-5【基础】 函数的图象在点处的切线方程为__________.
【正确答案】
13-6【巩固】 函数f(x)=lnx+x的图象在x=1处的切线方程为___.
【正确答案】 2x﹣y﹣1=0
【原卷 14 题】 知识点 正弦函数的定义域、值域和最值,平面向量的数量积,数量积的坐标表示
【正确答案】
【试题解析】
14-1【巩固】 已知向量,,,则__________.
【正确答案】
14-2【提升】 设,,.若,则实数的值等于___________.
【正确答案】
14-3【提升】 设,向量,,,且,,则_________.
【正确答案】
14-4【基础】 已知向量,若向量与垂直,则m=________..
【正确答案】
14-5【巩固】 已知平面向量,则的夹角为________.
【正确答案】 (或135°)
14-6【基础】 已知,,若,则的值是______.
【正确答案】 或2
【原卷 15 题】 知识点 椭圆的弦长、焦点弦
【正确答案】 8
【试题解析】
15-1【基础】 已知椭圆左、右焦点为,,上、下顶点为,,则四边形的面积为______.
【正确答案】
15-2【提升】 设P是椭圆=1上的一点,且,则△PF1F2的面积为_________.
【正确答案】 9
15-3【巩固】 为椭圆的两个焦点,点在椭圆上,且满足,则三角形的面积为_____________________;
【正确答案】 64.
15-4【基础】 椭圆的两个焦点与短轴的一个端点构成的三角形的面积等于________.
【正确答案】 2
15-5【巩固】 .已知、是椭圆的两个焦点,为椭圆上一点,且,则的面积 .
【正确答案】 9
15-6【提升】 已知为椭圆C: (a>b>0)上一点,若,则_____________.
【正确答案】 3
【原卷 16 题】 知识点 三角函数图象的综合应用,余弦函数的单调性,正(余)弦型三角函数的图象
【正确答案】 2
【试题解析】
16-1【巩固】 函数的图象与轴相交于点,如图是它的部分图象,若函数图象相邻的两条对称轴之间的距离为,则_________.
【正确答案】
16-2【基础】 已知函数的图象如图所示,则函数的解析式为__________.
【正确答案】
16-3【提升】 已知,若函数的图像如图所示,则_________
【正确答案】
16-4【巩固】 将函数的图象向左平移个单位,得到函数的图象,若函数在上为增函数,则的取值范围是___________.
【正确答案】
16-5【提升】 设函数,若对于任意实数,在区间上至少有2个零点,至多有3个零点,则的取值范围是________.
【正确答案】
16-6【基础】 已知函数的部分图象如图所示,是某个三角形的内角,若关于的不等式在上恒成立,则的取值范围为______.
【正确答案】
【原卷 17 题】 知识点 独立性检验
【正确答案】 (1)75%;60%;(2)能.
【试题解析】
17-1【基础】 在500人身上试验某种血清预防感冒作用,把他们一年中的感冒记录与另外500名未用血清的人的感冒记录作比较,结果如表所示.问:该种血清能否起到预防感冒的作用?
未感冒 感冒 合计
使用血清 258 242 500
未使用血清 216 284 500
合计 474 526 1000
【正确答案】 有99%的把握认为该血清能起到预防感冒的作用.
17-2【巩固】 调查某医院一段时间内婴儿出生的时间和性别的关联性,得到如下的列联表:
单位:人
性别 出生时间 合计
晚上 白天
女 24 31 55
男 8 26 34
合计 32 57 89
依据的独立性检验,能否认为性别与出生时间有关联?解释所得结论的实际含义.
【正确答案】 在犯错的概率不超过0.1的前提下可以认为性别与出生时间有关联.
17-3【巩固】 为了保障全国第四次经济普查顺利进行,国家统计局选择了江苏、河北、湖北、宁夏、重庆作为国家综合试点地区,逐级进行普查.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记.由于种种情况可能会导致人户登记不够顺利,这为正式普查提供了宝贵的试点经验.某普查小区,共有50家企事业单位,150家个体经营户,普查情况如下表所示:
顺利 不顺利 合计
企事业单位 40 50
个体经营户 50 150
合计
(1)补全列联表,并根据列联表判断是否有90%的把握认为“此普查小区的人户登记是否顺利与普查对象的类别有关”;
(2)根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
【正确答案】 (1)列联表见解析;有的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;(2)答案见解析.
17-4【提升】 有甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计后,得到如下的列联表:
班级与成绩列联表:
优秀 不优秀 总计
甲班 10 35 45
乙班 7 38 45
总计 17 73 90
试问能有多大把握认为“成绩与班级有关系”?
参考公式及数据:,其中.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
【正确答案】 没有充分证据认为“成绩与班级有关系”.
17-5【基础】 某杜区为了解居民参加体育锻炼的情况,从该社区中随机抽取了18名男性居民和12名女性居民,对他们参加体育锻炼的情况进行问卷调查.现按是否参加体育锻炼将居民分成两类:甲类(不参加体育锻炼)、乙类(参加体育锻炼),调查结果如下表:
(1)根据上表中的统计数据,完成下面的2 ×2列联表:
(2)通过计算判断是否有95%的把握认为参加体育锻炼与否跟性别有关
附
【正确答案】 (1)表格见解析;(2)没有的把握认为参加体育锻炼与否跟性别有关.
17-6【提升】 某中学高二甲、乙两个兴趣班进行了一次数学对抗赛,该对抗赛试题满分为150分,规定:成绩不小于135分为“优秀”,成绩小于135分为“非优秀”,对这两个班的所有学生的数学成绩统计后,得到如图条形图.
(1)根据图中数据,完成如下的2×2列联表;
甲班 乙班 总计
优秀
非优秀
总计
(2)计算随机变量的值(精确到0.001),并由此判断:能否有90%的把握认为“成绩与班级有关”?
参考数据:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
参考公式:,其中
【正确答案】 (1)答案见解析;(2),没有90%的把握认为“成绩与班级有关”.
【原卷 18 题】 知识点 数列求和,等差数列及其通项公式,等比数列的通项公式,an与Sn的关系——等差数列
【正确答案】 答案见解析
【试题解析】
18-1【基础】 已知正项等比数列的前项和为,,且________,从下列二个条件:
①; ②,,成等差数列;
中选择一个条件(填上序号),解决下列问题:
(1)求数列的通项公式;
(2)设数列满足,求数列的前项和.
【正确答案】 选①和②得结果相同,(1);(2)
18-2【巩固】 已知数列中,,_____,其中.
(Ⅰ)求数列的通项公式;
(Ⅱ)设,求证:数列是等比数列;
(Ⅲ)求数列的前项和.
从①前项和,①,②,③且,这三个条件中任选一个,补充在上面的问题中并作答.
【正确答案】 选①②③结果均相同,(Ⅰ);(Ⅱ)见解析;(Ⅲ)
18-3【提升】 设等差数列的前n项和为.
(1)求数列的通项公式及;
(2)若 ,求数列的前n项和.
在①;②;③这三个条件中任选一个补充在第(2)问中,并对其求解.
(注意:如果选择多个条件分别解答,按第一个解答计分.)
【正确答案】 (1);(2)答案不唯一,具体见解析.
18-4【巩固】 设数列的前项和为,,是等差数列,,公差,且,,成等比数列.
(1)求数列和的通项公式;
(2)设,数列的前项和为.若对任意的,恒成立,求实数的取值范围.
【正确答案】 (1),;(2).
18-5【提升】 在①,②,③这三个条件中任选一个,补充在下面问题中并作答.
已知是公差不为的等差数列,其前项和为,___________且 成等比数列.
(1)求数列的通项公式;
(2)设数列是各项均为正数的等比数列,且,,求数列的前项和.
【正确答案】 (1)若选①,,若选②,,若选③,;(2)若选①,
,若选②, ,若选③, .
18-6【基础】 已知数列的前项和满足.
(1)求;
(2)已知__________,求数列的前项和.
从下列三个条件中任选一个,补充在上面问题的横线中,然后对第(2)问进行解答.
条件:①
②
③
注:如果选择多个条件分别解答,以第一个解答计分.
【正确答案】 (1);(2)答案见解析.
【原卷 19 题】 知识点 平面的法向量,空间位置关系的向量证明,空间角的向量求法
【正确答案】
【试题解析】
19-1【基础】 如图在三棱锥P-ABC中,平面PAB⊥平面PBC,PB⊥BC,PD=DB=BC=AB=AD=2.
(1)证明:PA⊥平面ABC;
(2)求二面角B-AD-C的余弦值.
【正确答案】 (1)证明见解析;(2).
19-2【巩固】 如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥平面ABCD;
(2)若∠CBA=60°,求平面C1OB1与平面OB1D夹角的余弦值.
【正确答案】 (1)证明见解析;(2).
19-3【提升】 如图,在矩形中,,E为的中点,将沿折起到的位置,使得平面平面.
(1)证明:平面;
(2)求二面角的余弦值.
【正确答案】 (1)证明见解析;(2).
19-4【提升】 如图1,在边长为4的菱形ABCD中,∠BAD=60,DEAB于点E,将△ADE沿DE折起到△A1DE的位置,使A1DDC,如图2.
(1)求证:A1E平面BCDE;
(2)求二面角E—A1B—C的余弦值.
【正确答案】 (1)证明见解析;(2).
19-5【基础】 如图所示,在三棱柱中,,,四边形为菱形,,,D为的中点.
(1)证明:平面;
(2)若,求二面角的余弦值.
【正确答案】 (1)证明见解析;(2).
19-6【巩固】 如图在四棱锥中,底面为正方形,为等边三角形,E为中点,平面平面.
(1)求证:平面;
(2)求二面角的余弦值.
【正确答案】 (1)证明见解析;(2).
【原卷 20 题】 知识点 直线与圆的位置关系,抛物线标准方程的求法,抛物线的对称性
【正确答案】
【试题解析】
20-1【提升】 已知抛物线()的顶点为,直线与拋物线的交点(异于点)到点的距离为,
(1)求的标准方程;
(2)过点作斜率为()的直线与交于点(异于点),直线关于直线对称的直线与交于点(异于点),求证:直线过定点.
【正确答案】 (1);(2)证明见解析.
20-2【巩固】 如图,已知,直线,是平面上的动点,过点P作l的垂线,垂足为点Q,且.
(1)求动点P的轨迹C的方程;
(2)过点F的直线交轨迹C于A、B两点,交直线l于点M;
①已知,求的值;
②求的最小值.
【正确答案】 (1);(2)①;②.
20-3【提升】 已知椭圆:的焦距为,点在椭圆上,且的最小值是(为坐标原点).
(1)求椭圆的标准方程.
(2)已知动直线与圆:相切,且与椭圆交于,两点.是否存在实数,使得?若存在,求出的值;若不存在,请说明理由.
【正确答案】 (1);(2)存在
20-4【基础】 已知动圆过点,且与直线相切,设圆心的轨迹为曲线.
(1)求曲线的方程;
(2)设直线交曲线于,两点,以为直径的圆交轴于,两点,若,求的取值范围.
【正确答案】 (1);(2).
20-5【巩固】 已知抛物线C:()的焦点为F,原点O关于点F的对称点为Q,点关于点Q的对称点,也在抛物线C上
(1)求p的值;
(2)设直线l交抛物线C于不同两点A B,直线 与抛物线C的另一个交点分别为M N,,,且,求直线l的横截距的最大值.
【正确答案】 (1);(2)最大横截距为.
20-6【基础】 已知抛物线C:y2=4x,A,B,其中m>0,过B的直线l交抛物线C于M,N.
(1)当m=5,且直线l垂直于x轴时,求证:△AMN为直角三角形;
(2)若=+,当点P在直线l上时,求实数m,使得AM⊥AN.
【正确答案】 (1)证明见解析;(2)m=6.
【原卷 21 题】 知识点 利用导数研究函数的单调性,导数在函数中的其他应用
【正确答案】
【试题解析】
21-1【提升】 设函数().
(1)当时,试求下列问题:
①函数的单调区间;
②函数在的零点的个数;
(2)若函数在内有两个零点,求出的取值范围.
【正确答案】 (1)①的单调增区间为和,的单调递减区间为;②函数在有一个零点;(2).
21-2【巩固】 已知函数
(1)若在处有极值,求实数的值;
(2)求函数的单调区间;
(3)若函数有两个零点,求实数的范围.
【正确答案】 (1);(2)答案见解析;(3).
21-3【提升】 已知函数()
(1)当时,求的单调区间;
(2)若过点可作函数图像的三条不同切线,求实数的取值范围.
【正确答案】 (1)单调区间:,,;(2).
21-4【基础】 已知函数(为自然对数的底数)在处的切线与轴平行.
(1)求的单调区间;
(2)若在内有两个零点,求的取值范围.
【正确答案】 (1)在上单调递减,在上单调递增;(2).
21-5【巩固】 已知函数的定义域为.
(1)求的单调区间;
(2)讨论函数在上的零点个数
【正确答案】 (1)的单调递减区间为,单调递增区间为,(2)答案见解析
21-6【基础】 若函数,当时,函数有极值为.
(1)求函数的解析式;
(2)若有个解,求实数的取值范围.
【正确答案】 (1);(2).
【原卷 22 题】 知识点 极坐标与直角坐标的互化,圆的参数方程
【正确答案】
【试题解析】
22-1【巩固】 在平面直角坐标系中,曲线:,曲线:(为参数),以坐标原点为极点,轴正半轴为极轴建立极坐标系
(1)求曲线,的极坐标方程:
(2)射线:(,)分别交曲线,于,两点,求的最大值.
【正确答案】 (1):,:;(2)最大值为.
22-2【提升】 在直角坐标系中,以坐标原点为极点,轴的正半轴为极轴建立坐标系,曲线的极坐标方程为,曲线的参数方程为(为参数,).
(1)写出曲线的直角坐标方程;
(2)若曲线与有两个不同的交点,求实数的取值范围.
【正确答案】 (1)(2)
22-3【基础】 在直角坐标系xOy中,曲线C的参数方程为(m为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)求直线l的直角坐标方程;
(2)若直线l与曲线C交于点A,点P在曲线C上运动,求线段PA中点M轨迹的极坐标方程.
【正确答案】 (1);(2).
22-4【基础】 在平面直角坐标系中,圆C的参数方程为(α为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系,且长度单位相同.
(1)求圆C的极坐标方程;
(2)若过原点的直线l被圆C截得的弦长为2,求直线l的倾斜角.
【正确答案】 (1);(2)直线l的倾斜角为或.
22-5【提升】 以直角坐标系的原点为极点,轴非负半轴为极轴建立极坐标系.在极坐标系中,曲线,点.在直角坐标系中,,,直线的参数方程为(为参数)
(1)将曲线的极坐标方程化为直角坐标方程,并判与4的大小关系;
(2)直线与曲线交于、两点,为曲线的右顶点,求的面积.
【正确答案】 (1),;(2).
22-6【巩固】 已知曲线,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)写出曲线C的参数方程,直线l的直角坐标方程;
(2)设P是曲线C上任一点,求P到直线l的距离的最大值.
【正确答案】 (1)(为参数),;(2).
【原卷 23 题】 知识点 含绝对值不等式的解法,函数的图象
【正确答案】
【试题解析】
23-1【基础】 已知函数.
(1)解不等式;
(2)若正实数,满足,且函数的最小值为,求证:.
【正确答案】 (1);(2)证明见解析.
23-2【提升】 设实数x,y,z满足.
(1)证明:;
(2)若对任意的实数x,y,z,a恒成立,求实数m的取值范围.
【正确答案】 (1)证明见解析;(2)或.
23-3【提升】 已知函数.
(1)求不等式的解集;
(2)不等式的最小值为,若,为正数,且,证明:.
【正确答案】 (1);(2)证明见解析.
23-4【基础】 已知函数.
(1)解不等式;
(2)记函数的最小值为,且,其中均为正实数,求证:
【正确答案】 (1);(2)证明见解析.
23-5【巩固】 已知.
(1)求不等式的解集;
(2)若,求证:.
【正确答案】 (1);(2)证明见解析.
23-6【巩固】 设函数的最小值为.
(1)求的值;
(2)若,且,,用表示,,中的最大值,证明:
【正确答案】 (1)1;(2)证明见解析.
2021年高考理科数学甲卷 高三变式题库
/92 73是第21个素数,将其反过来37是第12个素数,同时7x3=21。
答案解析
2021年高考理科数学甲卷 高三变式题库
2021年高考理科数学甲卷 高三变式题库
/92 打好数学基础有两个必经过程:先学习、接受“由薄到厚”;再消化、提炼“由厚到薄”。——华罗庚
学习数学要多做习题,边做边思索。先知其然,然后知其所以然。——苏步青 /92
共性错题精讲
1-1【基础】 【正确答案】 B
【试题解析】 分析:
求出函数y=的定义域,得到集合N,再利用集合的交集的定义求解.
详解:
集合N={x|y=}={x|(x+2)(x﹣4)≥0}={x|x≤﹣2或x≥4},
∴M∩N={x|﹣4<x≤-2}.
故选:B.
1-2【巩固】 【正确答案】 A
【试题解析】 分析:
解出集合,利用并集的定义可求得集合.
详解:
,因此,.
故选:A.
1-3【巩固】 【正确答案】 C
【试题解析】 分析:
先求出集合P,Q,再利用集合的交集运算求解.
详解:
集合P={x∈N|x≤3}={0,1,2,3},Q={x|x2≤x+2}={x|﹣1≤x≤2},
∴P∩Q={0,1,2}.
故选:C.
1-4【基础】 【正确答案】 A
【试题解析】 分析:
化简得,根据集合并集运算即可.
详解:
解:化简得,
所以
故选:A.
1-5【提升】 【正确答案】 A
【试题解析】 分析:
先利用一元二次不等式的解法化简集合A,再利用交集运算求解.
详解:
∵,,
∴.
故选:A.
1-6【提升】 【正确答案】 A
【试题解析】 分析:
根据函数的定义域分别求出集合A、B,再根据交集的运算即可得出答案.
详解:
解:,
,
所以.
故选:A.
2-1【基础】 【正确答案】 C
【试题解析】 分析:
根据给定的柱状图分别求得健身前后各个区间上的人数,进行比较,即可求解.
详解:
根据给定的健身前后的体重柱状图,可得健身前体重在区间有人,健身后有,所以体重在区间内的人数增加了4个,所以A正确;
由健身前体重在的人数为人,健身后有,所以健身前后体重在的人数不变,所以B正确;
由健身前后体重再和的人数有明显变化,所以健身对体重有明显效果,所以C不正确;
由健身前体重在的人数为人,健身后为0人,所以原来体重在区间内的肥胖者体重都有减少,所以D正确.
故选:C.
点睛:
本题主要考查了统计图表的应用,其中解答中图表中的数据,分别计算求得健身前后各个区间的人数,进行比较是解答的关键,着重考查图表提取信息的能力,以及数据处理能力.
2-2【巩固】 【正确答案】 C
【试题解析】 分析:
根据频率分布直方图逐一计算分析.
详解:
A:用电量最多的一组有:人,故正确;
B:不低于度的有:人,故正确;
C:人均用电量:,故错误;
D:用电量在的有:人,所以,故正确;
故选C.
点睛:
本题考查利用频率分布直方图求解相关量,难度较易.频率分布直方图中平均数的求法:每一段的组中值后结果相加.
2-3【提升】 【正确答案】 B
【试题解析】 详解:
若①正确,则对应的频率为,
则对应的频率为,则②错误;
电子元件的平均寿命为,
则③正确;
寿命超过的频率为,则④正确,故不符合题意;
若②正确,则对应的频率为,则①错误;
电子元件的平均寿命为,
则③错误;
寿命超过的频率为,则④错误,故符合题意.
故选:B.
2-4【巩固】 【正确答案】 D
【试题解析】 分析:
利用频率分布直方图的性质直接求解.
详解:
解:对于,90分以上为优秀,由频率分布直方图得优秀的频率为,
从全体考生中随机抽取1000人,则其中得优秀考试生约有:人,故正确;
对于,由频率分布直方图得,的频率为,
,的频率为:,
若要全省的合格考通过率达到,则合格分数线约为44分,故正确;
对于,若同一组中数据用该组区间中间值作代表值,可得考试物理成绩的平均分约为:
分,故正确;
对于,,的频率为:,
,的频率为,
该省考生物理成绩的中位数为:分,故错误.
故选:.
点睛:
本题考查频数、合格分数线、平均数、中位数的求法,考查频率分布直方图的性质等基础知识,考查运算求解能力,属于基础题.
2-5【提升】 【正确答案】 C
【试题解析】 分析:
根据众数、中位数、平均值的概念等求值即可判断.
详解:
对于A,样本的众数为,A对;
对于B,设样本的中位数为,,解得,B对;
对于C,由直方图估计样本平均值为
,C错误;
对于D,2000名男生中体重大于的人数大约为,D对.
故选:C.
2-6【基础】 【正确答案】 C
【试题解析】 分析:
由频率分布直方图中的数据,以及频率、中位数、平均数的计算公式,逐项判定,即可求解.
详解:
根据此频率分布直方图,成绩在内的人数为人,所以A正确;
这名学生中成绩在内的频率为,所以B正确;
根据此频率分布直方图,可得这名学生成绩的中位数,所以C错误;
根据频率分布直方图的平均数的计算公式,可得:
,所以D正确.
故选:C.
3-1【提升】 【正确答案】 C
【试题解析】 分析:
先根据将化简,再根据复数的模的计算公式即可求出.
详解:
因为,
所以 .
故选:C.
点睛:
本题主要考查复数的模的计算公式的应用,属于容易题.
3-2【基础】 【正确答案】 A
【试题解析】 分析:
把已知等式变形,再利用复数代数形式的乘除运算化简得答案.
详解:
故选:A
3-3【提升】 【正确答案】 A
【试题解析】 分析:
由复数除法法则计算.
详解:
由已知
.
故选:A.
3-4【基础】 【正确答案】 B
【试题解析】 分析:
利用复数除法计算公式,即可得到结果.
详解:
.
故选:B
3-5【巩固】 【正确答案】 D
【试题解析】 分析:
由题意利用复数的运算法则整理计算即可求得最终结果.
详解:
由题意可得:.
故选:D.
3-6【巩固】 【正确答案】 A
【试题解析】 分析:
根据复数的除尘法则计算.
详解:
由已知.
故选:A.
4-1【基础】 【正确答案】 B
【试题解析】 分析:
根据题意构建指数函数模型,利用对数的运算进行计算即可得解.
详解:
设年后研发资金开始超过140万,
有,
所以,
由,所以,
所以第年研发资金开始超过140万元,
即2026年研发资金开始超过140万元.
故选:B
4-2【巩固】 【正确答案】 C
【试题解析】 分析:
利用对数的运算和对数函数的单调性求解.
详解:
当时,
,
当时,,
当时,,
当时,,
所以这4人中达到班级要求的有3人,
故选:C
4-3【基础】 【正确答案】 D
【试题解析】 分析:
根据已知条件列出式子求解即可.
详解:
解:由题意知:,
,
即,
即,
,
,
故正整数n的最小值为16.
故选:D.
4-4【提升】 【正确答案】 A
【试题解析】 分析:
根据题目所给数据求得,由此根据接收方收到明文“”,求得发送方发送的明文.
详解:
由其加密原理可知当时,,从而;
.
由解密原理可知当时,;
若接受方接到明文为“4”则有,,从而有,解得,
即发送方明文为.
故选:A
4-5【巩固】 【正确答案】 C
【试题解析】 分析:
根据小区内公共场所的声音的强度水平必须保持在50分贝以下,建立不等式,然后解对数不等式即可得到答案.
详解:
解:由题意可得,,即,
所以,解得,
所以声音强度的取值范围是,.
故选:C.
4-6【提升】 【正确答案】 A
【试题解析】 分析:
利用题设条件,计算出原信道容量的表达式,再列出在B不变时用所求平均噪声功率表示的信道容量的表达式,最后列式求解即得.
详解:
由题意可得,,则在信道容量未增大时,信道容量为,信道容量增大到原来的2倍时,,则,即,解得,
故选:A
5-1【提升】 【正确答案】 C
【试题解析】 分析:
由双曲线的定义可得,,结合已知条件可得,然后在直角三角形中利用勾股定理可求得答案
详解:
解:由双曲线的定义可得,,
因为,所以,
所以,即,
因为,
所以,所以,
由,得,
所以,得,
故选:C
5-2【提升】 【正确答案】 B
【试题解析】 分析:
设,则,然后由已知条件和双曲线的定义或求得,,再分别在和中,利用余弦定理列方程可求得,从而可求得离心率
详解:
解:设,则,
所以,
所以
因为,所以,
因为,所以
设,则,
在和中,由余弦定理得,
,
,
即,,
解得,
所以,
故选:B
5-3【巩固】 【正确答案】 D
【试题解析】 分析:
由题知,,计算得,由双曲线定义列出,计算可得离心率.
详解:
由题知,,又,且,则,
由双曲线定义得,,得
故选:D
5-4【巩固】 【正确答案】 A
【试题解析】 分析:
由圆的性质以及双曲线的定义得出,,再结合余弦定理以及离心率公式列出方程,求解即可.
详解:
取右焦点,连接
,
,即,
解得
故选:A
点睛:
关键点睛:解决本题的关键在于由余弦定理建立的齐次方程,从而得出离心率.
5-5【基础】 【正确答案】 D
【试题解析】 分析:
设的坐标为,函数的导数,根据条件可得,可解得,即,再根据双曲线的定义可求出其,从而得到离心率.
详解:
设的坐标为,由左焦点,所以
函数的导数,
则在处的切线斜率,
即,得,则,
设右焦点为,则,即,
,∴双曲线的离心率.
故选:D
5-6【基础】 【正确答案】 D
【试题解析】 分析:
由条件结合双曲线的定义可得,即,从而可得双曲线的离心率.
详解:
由双曲线的定义可得,∵,
∴,即,
则的离心率为.
故选:D.
6-1【巩固】 【正确答案】 A
【试题解析】 详解:
因为一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是
(0,0,2),(2,2,0),(0,2,0),(2,2,2).
画出几何体的直观图,如图
所以,以zOx平面为投影面,则得到正视图为AOC,
故选A.
6-2【基础】 【正确答案】 C
【试题解析】 分析:
本题首先可以通过三视图的几何性质得知三视图之间的联系,然后通过三视图的主视图与左视图来确定锥体的顶点所在的位置,最后对四个选项依次分析,即可得出结果.
详解:
本题中给出了主视图与左视图,故可以根据主视图与俯视图长对正,左视图与俯视图宽相等来找出正确选项,由主视图与左视图可知,锥体的顶点在左前方,
中的视图满足作图法则;中的视图满足作图法则;中的视图不满足锥体的顶点在左前方;中的视图满足作图法则,故选.
点睛:
本题考查了三视图的相关性质,主要考查了三视图中的主视图、左视图与俯视图的联系,考查空间想象能力,体现了基础性,是简单题.
6-3【提升】 【正确答案】 A
【试题解析】 详解:
试题分析:解题时在图的右边放扇墙(心中有墙),图所示方向的侧视图,由于平面仍在平面上,故侧视图中仍然看到左侧的一条垂直下边线段的线段,可得答案A,故选A.
考点:1、几何体的三视图;2、空间想象能力.
6-4【提升】 【正确答案】 B
【试题解析】 分析:
利用三视图的作图法则,对选项判断,①的三视图相同,圆锥,四棱锥的两个三视图相同,棱台都不相同,推出选项即可.
详解:
正方体的三视图分别为:正方形、正方形、正方形,圆锥的三视图分别为,三角形、三角形、圆和点.三棱台的三视图分别为:梯形和线段、梯形、大三角形内有小三角形,正四棱锥的三视图分别为:三角形、三角形、正方形和对角线,易知只有②④符合条件,故选B.
点睛:
本题主要考查几何体的三视图的识别能力,作图能力,学生的空间想象能力,三视图的投影规则是主视、俯视长对正;主视、左视高平齐,左视、俯视 宽相等,熟记常见几何体的三视图是解题的关键,属于基础题.
6-5【基础】 【正确答案】 D
【试题解析】 详解:
在空间直角坐标系中,根据所给的条件标出已知的四个点,结合三视图的画图规则,可得三棱锥的正视图和俯视图分别为④②.选D.
6-6【巩固】 【正确答案】 D
【试题解析】 详解:
由题意知三棱锥的侧视图即为三棱锥在侧面上的正投影,点点的投影为,点的投影为,点的投影为,故侧视图为上宽下窄的梯形,且左下到右上的对角线为实线,左上到右下的对角线为虚线,故D选项满足.选D.
点睛:三视图的三种题型
(1)已知几何体画出三视图,解题时要注意画三视图的规则;
(2)已知三视图还原几何体,要综合三个视图得到几何体的形状;
(3)已知三视图研究几何体,如根据三视图求几何体的体积或表面积等.
7-1【提升】 【正确答案】 D
【试题解析】 分析:
根据已知求得的范围,然后根据的正负分类讨论确定的单调性.
详解:
因为,所以,,即,
若,,,是递增数列,排除AC,
若,则,,易知,,是摆动数列,排除B,
当时,是递增数列,是最小项.
当时,,,
所以,所以中是最小项.D正确.
故选:D.
点睛:
关键点点睛:本题考查数列的单调性,解题关键是通过与的关系进行判断,难点是摆动数列的最小项问题,需要利用进行证明.
7-2【巩固】 【正确答案】 D
【试题解析】 分析:
由题可得,利用条件可得出,进而可得.
详解:
∵,
∴,
∵,
>0,
∵a1=2,
∴,……
∴数列{bn}是递减数列.
故选:D.
7-3【巩固】 【正确答案】 D
【试题解析】 分析:
由已知式变形,再写一次(用换)可得,这样.然后根据利用等差中项法判断等差数列,利用定义判断数列的单调性.
详解:
由题意知,则,
从而,
则,
因此.
对于选项A,C,当时,
,
从而,
故数列不可能是等差数列,因此选项A错误,
若,则,
从而,
即,
因此数列是递减的,因此选项C错误;
对于选项B,D,当时,
,
从而,
故数列不可能是等差数列,因此选项B错误,
若,则,
从而,
即,
因此数列是递减的,选项D正确.
故选:D.
点睛:
关键点点睛:本题考查等差数列的判断,数列的单调性,解题关键是对已知递推关系变形得出是常数,根据利用等差数列和单调性的概念判断.
7-4【提升】 【正确答案】 D
【试题解析】 分析:
根据数列的单调性的定义,结合不等式的性质、对钩函数的单调性进行求解即可.
详解:
,,
所以当时,,
当时,数列是递增数列,
因此有或,而,所以,
因此必有或,而,
所以有或,因此选项A,C不正确;
因为,所以选项B不正确;
当时,数列是递增数列,故,
,而函数在时,单调递增,故数列是单调递增数列;
,而函数在时,单调递增,故数列为单调递增数列.
故选:D
点睛:
本题考查了数列的单调性判断,考查了对钩函数的单调性的应用,考查了数学运算能力.
7-5【基础】 【正确答案】 B
【试题解析】 分析:
利用特例法证明充分性不成立;当成立时,两边平方可得 ,则数列为递减数列成立,即必要性满足.
详解:
由题意可得:数列的项都是实数,
当数列为递减数列时,如:数列的通项为,
此时不成立,即充分性不满足;
当成立时,有,
两边平方可得:即有,
因此数列为递减数列成立,
所以“数列为递减数列”是“”的必要不充分条件
故选:B
点睛:
本题考查了递减数列概念以及判断充分条件,必要条件,属于一般题.
7-6【基础】 【正确答案】 B
【试题解析】 分析:
根据充分发条件的定义判断.
详解:
是递增数列,则必有,必要性满足,
若,,满足,但,数列不是递增数列,充分性不满足.
应是必要不充分条件,
故选:B.
点睛:
本题考查充分必要条件的判断,掌握充分必要条件的定义是解题关键.
8-1【基础】 【正确答案】 B
【试题解析】 分析:
在和中,利用正切值可求得,进而求得.
详解:
在中,(米),
在中,(米),
(米).
故选:.
点睛:
本题考查解三角形的实际应用中的高度问题的求解,属于基础题.
8-2【基础】 【正确答案】 C
【试题解析】 分析:
在中,由条件可得,再在中,由可得解.
详解:
如图所示,在中,由正弦定理可得 ,
由,,
所以,
在中,.
故选:C.
8-3【巩固】 【正确答案】 B
【试题解析】 分析:
设的高度为,在直角三角形中用表示出,由可求得得楼高.
详解:
设的高度为,
则由已知可得,,,
所以,解得,
所以楼高(米).
故选:B.
点睛:
本题考查解三角形的实际应用.属于基础题.
8-4【巩固】 【正确答案】 D
【试题解析】 分析:
由正弦得出,再结合正弦定理得到,进而能求.
详解:
由题意知:,所以
在中,,
在中,由正弦定理得 所以 ,
在中,
故选:D
8-5【提升】 【正确答案】 A
【试题解析】 分析:
利用平面相似的有关知识以及合分比性质即可解出.
详解:
如图所示:
由平面相似可知,,而 ,所以
,而 ,
即= .
故选:A.
点睛:
本题解题关键是通过相似建立比例式,围绕所求目标进行转化即可解出.
8-6【提升】 【正确答案】 A
【试题解析】 分析:
根据C点的仰角∠CAB=45°,山高BC=100 m,可求出AC,正弦定理求出AM,在三角形MAN中即可解出山高.
详解:
由题意∠CAB=45°,BC=100 m,,三角形ABC为直角三角形,可得,在中,∠MAC=75°,∠MCA=60°,则∠AMC=45°
由正弦定理有:
即
故
在直角三角形中,
可得
故选:
点睛:
解三角形应用题的一般步骤:
(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.
(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.
(3)根据题意选择正弦定理或余弦定理求解.
(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.
9-1【巩固】 【正确答案】 A
【试题解析】 详解:
,,
,即,故
故选
9-2【提升】 【正确答案】 C
【试题解析】 分析:
由所给等式利用同角三角函数的关系可求得,再利用降幂公式及二倍角公式将整理为,代入相应值即可得解.
详解:
由可得
所以,即,即
故选:C
点睛:
关键点睛:本题考查同角三角函数的关系、降幂公式、二倍角公式,解答本题的关键是由条件有,从而可得,由可解,属于中档题.
9-3【基础】 【正确答案】 D
【试题解析】 分析:
首先由角知,再利用同角三角函数平方关系求,二倍角余弦公式以及诱导公式求即可.
详解:
,
,
又,
.
.
故选:D.
9-4【巩固】 【正确答案】 A
【试题解析】 分析:
由同角三角函数的基本关系可求得的值,再利用弦化切以及二倍角的正弦和余弦公式可求得所求代数式的值.
详解:
,是第三象限角,,
因此,,
故选:A.
点睛:
方法点睛:三角函数的化简求值的规律总结:
(1)给角求值:一般给出的角是非特殊角,需观察所给角与特殊角的关系,利用三角变换转化为特殊角的三角函数问题;
(2)给值求值:即给出某些角的三角函数值,求另外一些角的三角函数值,解题关键在于“变角”,使相关角相同或具有某种关系;
(3)给值求角:实质上可转化为“给值求值”,即通过求角的某个三角函数值来求角(注意角的取值范围).
9-5【提升】 【正确答案】 C
【试题解析】 分析:
将式子先利用二倍角公式和平方关系配方化简,然后增添分母(),进行齐次化处理,化为正切的表达式,代入即可得到结果.
详解:
将式子进行齐次化处理得:
.
故选:C.
点睛:
易错点睛:本题如果利用,求出的值,可能还需要分象限讨论其正负,通过齐次化处理,可以避开了这一讨论.
9-6【基础】 【正确答案】 A
【试题解析】 分析:
由同角三角函数的基本关系计算可得、,再根据两角差的正切公式计算可得.
详解:
解:因为,所以,又,
所以,则,
所以.
故选:
点睛:
本题考查三角恒等变换,考查运算求解能力,属于基础题.
10-1【基础】 【正确答案】 B
【试题解析】 分析:
甲和乙参加的概率为,甲和乙演讲顺序不相邻的概率为,由此能求出甲和乙参加,且演讲顺序不相邻的概率.
详解:
甲和乙参加的概率为,甲和乙演讲顺序不相邻的概率为,
所求概率为;或直接为.
故选:B.
10-2【提升】 【正确答案】 D
【试题解析】 详解:
从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,
基本事件总数n=5×5=25,
抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有:
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),
共有m=10个基本事件,
∴抽得的第一张卡片上的数大于第二张卡片上的数的概率p=
故答案为D.
10-3【基础】 【正确答案】 B
【试题解析】 分析:
本题首先用列举法写出所有基本事件,从中确定符合条件的基本事件数,应用古典概率的计算公式求解.
详解:
设其中做过测试的3只兔子为,剩余的2只为,则从这5只中任取3只的所有取法有,共10种.其中恰有2只做过测试的取法有共6种,
所以恰有2只做过测试的概率为,选B.
点睛:
本题主要考查古典概率的求解,题目较易,注重了基础知识、基本计算能力的考查.应用列举法写出所有基本事件过程中易于出现遗漏或重复,将兔子标注字母,利用“树图法”,可最大限度的避免出错.
10-4【提升】 【正确答案】 D
【试题解析】 分析:
利用分步计数原理求出不同的涂色方案有420种,其中,区域涂色不相同的情况有120种,由此根据古典概型概率公式能求出区域涂色不相同的概率.
详解:
提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,
根据题意,如图,设5个区域依次为,分4步进行分析:
,对于区域,有5种颜色可选;
,对于区域与区域相邻,有4种颜色可选;
,对于区域,与区域相邻,有3种颜色可选;
,对于区域,若与颜色相同,区域有3种颜色可选,
若与颜色不相同,区域有2种颜色可选,区域有2种颜色可选,
则区域有种选择,
则不同的涂色方案有种,
其中,区域涂色不相同的情况有:
,对于区域,有5种颜色可选;
,区域,有4种颜色可选;
对于区域,有3种颜色可选;
,若与颜色相同,区域有2种颜色可选;
若与颜色不相同,区域有2种颜色可选,区域有1种颜色可选;
所以区域有种选择;
不同的涂色方案有种,
区域涂色不相同的概率为 ,故选D.
点睛:
本题考查古典概型概率公式的应用,考查分步计数原理等基础知识,考查运算求解能力,是中档题.在求解有关古典概型概率的问题时,首先求出样本空间中基本事件的总数,其次求出概率事件中含有多少个基本事件,然后根据公式求得概率.
10-5【基础】 【正确答案】 A
【试题解析】 分析:
本题主要考查利用两个计数原理与排列组合计算古典概型问题,渗透了传统文化、数学计算等数学素养,“重卦”中每一爻有两种情况,基本事件计算是住店问题,该重卦恰有3个阳爻是相同元素的排列问题,利用直接法即可计算.
详解:
由题知,每一爻有2种情况,一重卦的6爻有情况,其中6爻中恰有3个阳爻情况有,所以该重卦恰有3个阳爻的概率为=,故选A.
点睛:
对利用排列组合计算古典概型问题,首先要分析元素是否可重复,其次要分析是排列问题还是组合问题.本题是重复元素的排列问题,所以基本事件的计算是“住店”问题,满足条件事件的计算是相同元素的排列问题即为组合问题.
10-6【基础】 【正确答案】 C
【试题解析】 分析:
分别安排各场馆的志愿者,利用组合计数和乘法计数原理求解.
详解:
首先从名同学中选名去甲场馆,方法数有;
然后从其余名同学中选名去乙场馆,方法数有;
最后剩下的名同学去丙场馆.
故不同的安排方法共有种.
故选:C
点睛:
本小题主要考查分步计数原理和组合数的计算,属于基础题.
11-1【巩固】 【正确答案】 C
【试题解析】 分析:
求出矩形的对角线长,进而可得球心到矩形所在平面的距离即棱锥的高,再由棱锥的体积公式即可得解.
详解:
∵矩形的顶点都在半径为5的球面上,且,,
∴矩形的对角线长为,
∴球心到矩形所在平面的距离为,
所以棱锥的体积.
故选:C.
点睛:
本题考查了球的几何特征的应用及几何体体积的求解,考查了运算求解能力与空间思维能力,属于基础题.
11-2【基础】 【正确答案】 D
【试题解析】 分析:
先由球的截面的性质可得球的半径,再由正方体外接球的直径即为体对角线的长即可得解.
详解:
由题意,的外接圆半径为,
设该球的半径为,可得,所以,
设该球内接正方体的棱长为,所以,所以.
故选:D.
11-3【提升】 【正确答案】 C
【试题解析】 分析:
设三角形ABC的外接圆的圆心为O',根据球的截面性质可知OO'⊥平面ABC,利用正弦定理求得AO',计算球的半径,进而求得体积.
详解:
设三角形ABC的外接圆的圆心为O',根据球的截面性质可知OO'⊥平面ABC,
如图所示,∵,∴AO'=,
∴OA=
∴球的体积为,
故选:C.
11-4【巩固】 【正确答案】 D
【试题解析】 分析:
求出外接圆半径,再利用球面的截面小圆的性质求出球半径即可作答.
详解:
因,,则,即,于是得外接圆半径,
又点、、在同一个球面上,且球心到平面的距离为1,则球半径,
所以球的表面积为.
故选:D
11-5【提升】 【正确答案】 C
【试题解析】 分析:
由题意画出图形,由是面积为的等边三角形,可得,再由球的体积为,求出球的半径,而,再利用勾股定理可求出结果
详解:
由题意可知图形如图:是面积为的等边三角形,
可得,
∴,
可得:,
球的体积,解得,
所以到平面的距离为:.
故选:C.
点睛:
此题考查球截面性质,考查空间想象能力和计算能力,属于基础题
11-6【基础】 【正确答案】 D
【试题解析】 分析:
由截面圆的面积求出截面圆半径,根据截面圆半径、球的半径和球心到平面的距离之间的关系即可求解球的半径,进而求表面积.
详解:
如图所示:
设截面圆的半径为,球的半径为,球心到平面的距离为
因为截面圆的面积为,得,又
由图可得
则球的表面积为
故选:D.
12-1【巩固】 【正确答案】 A
【试题解析】 分析:
先求出函数的解析式,将代入计算即可.
详解:
因为函数在定义域上单调,且,
所以为常数,不妨设,则
由得,解得:,
所以,
所以.
故选:A
12-2【基础】 【正确答案】 C
【试题解析】 分析:
根据题意求得函数的周期,结合函数性质,得到,在代入解析式求值,即可求解.
详解:
因为为上的偶函数,所以,
又因为对于,都有,
所以函数的周期,且当时,,
所以
故选:C.
12-3【巩固】 【正确答案】 A
【试题解析】 分析:
由奇函数和,可得周期,转化
,即得解
详解:
由题意,函数是上的奇函数,满足
因此函数的周期
故选:A
12-4【基础】 【正确答案】 B
【试题解析】 分析:
利用函数的奇偶性和周期性求解.
详解:
因为函数是定义域为R的奇函数,周期为2,且当时,,
所以 ,
故选:B
12-5【提升】 【正确答案】 B
【试题解析】 详解:
分析:由题意,得到函数是周期为的函数,进而可求得的值.
详解:由题意可得:,即函数是周期为的函数,
则,
故选B.
点睛:本题考查了函数的基本性质的应用,对于函数的三个性质:单调性、奇偶性和周期性,常将它们综合在一起考查,其中单调性与奇偶性结合、周期性与抽象函数相结合,并结合奇偶性求函数值,多以选择题、填空题的形式呈现,且主要有以下几种命题角度:
(1)函数的单调性与奇偶性相结合,注意函数的单调性及奇偶性的定义,以及奇、偶函数图象的对称性.
(2)周期性与奇偶性相结合,此类问题多考查求值问题,常利用奇偶性及周期性进行交换,将所求函数值的自变量转化到已知解析式的函数定义域内求解.
(3)周期性、奇偶性与单调性相结合,解决此类问题通常先利用周期性转化自变量所在的区间,然后利用奇偶性和单调性求解.
12-6【提升】 【正确答案】 A
【试题解析】 详解:
分析:根据奇函数与偶函数的定义,可求得函数的解析式;根据解析式确定’的值.
详解:令 ,
则,因为为偶函数
所以(1)
,因为 为奇函数
所以(2)
(1)-(2)得
(3),令 代入得
(4)
由(3)、(4)联立得
代入得
所以
所以
所以选A
点睛:本题考查了抽象函数解析式的求解,主要是利用方程组思想确定解析式.方法相对比较固定,需要掌握特定的技巧,属于中档题.
13-1【提升】 【正确答案】
【试题解析】 分析:
先将曲线变形,再通过求导求曲线在处的切线方程,再求面积.
详解:
由可得时,.,,则切线方程为即.
切线与两坐标轴的交点分别为,所以三角形的面积为.
点睛:
求过曲线上一点的切线方程一般有两种思路:1、设切线的斜率,联立曲线方程和直线方程通过判别式加以判断;2、通过求导求曲线在这个点处的斜率,进而求出切线方程.此题曲线是双曲线,若用判别式法求解,则求出的结果要注意检验.用求导求解要注意所得解析式中.
13-2【基础】 【正确答案】
【试题解析】 分析:
到处导函数,再求出切线方程,即可得到横纵截距之和.
详解:
由题:,
,,
所以在点处切线方程,即
当,
当,
所以该切线的横纵截距之和为.
故答案为:
点睛:
此题考查求曲线在某点处的切线方程,再求直线截距,关键在于根据题意准确计算.
13-3【巩固】 【正确答案】
【试题解析】 分析:
根据导数几何意义得切线斜率,再根据点斜式得结果.
详解:
因为,所以,因此在x=0处的切线斜率为,
因为x=0时,所以切线方程是
点睛:
本题考查导数几何意义,考查基本求解能力.属基础题.
13-4【提升】 【正确答案】
【试题解析】 详解:
设,则,
,
据此可得:,
且:,
据此可得:曲线在处的切线方程是,
整理为一般式即:.
点睛:导数运算及切线的理解应注意的问题
一是利用公式求导时要特别注意除法公式中分子的符号,防止与乘法公式混淆.
二是直线与曲线公共点的个数不是切线的本质,直线与曲线只有一个公共点,直线不一定是曲线的切线,同样,直线是曲线的切线,则直线与曲线可能有两个或两个以上的公共点.
三是复合函数求导的关键是分清函数的结构形式.由外向内逐层求导,其导数为两层导数之积.
13-5【基础】 【正确答案】
【试题解析】 分析:
求导得到,计算,,得到切线方程.
详解:
,则,故,
故切线方程为:,即
故答案为:
点睛:
本题考查了切线方程,意在考查学生的计算能力.
13-6【巩固】 【正确答案】 2x﹣y﹣1=0
【试题解析】 分析:
求出f(x)的导数,可得切线的斜率和切点,即可得到所求切线的方程.
详解:
函数f(x)=lnx+x的导数为,
可得函数f(x)的图象在x=1处的切线斜率为k=2,
切点为(1,1),
可得切线的方程为y﹣1=2(x﹣1);即2x﹣y﹣1=0.
故答案为2x﹣y﹣1=0.
点睛:
本题考查利用导数求切线的方程,是基本题.
14-1【巩固】 【正确答案】
【试题解析】 分析:
首先根据向量线性运算的坐标表示求出,再计算数量积即可;
详解:
解:因为,,
所以,
所以
故答案为:
14-2【提升】 【正确答案】
【试题解析】 分析:
先求的坐标,再利用列方程即可求解.
详解:
因为,,所以,
因为,
所以,解得,
故答案为:.
14-3【提升】 【正确答案】
【试题解析】 分析:
根据向量垂直和平行的坐标运算法则计算得,,得出,再根据向量的模的坐标公式即可求得结果.
详解:
因为向量,,,
且,,
∴
解得,;
∴,;
∴,
∴.
故答案为:
14-4【基础】 【正确答案】
【试题解析】 分析:
根据向量垂直的坐标表示以及平面向量的数量积列方程可解得结果.
详解:
因为向量,,且向量与垂直,
所以,
所以,
所以,解得.
故答案为:
14-5【巩固】 【正确答案】 (或135°)
【试题解析】 分析:
根据向量,求得向量的坐标,再利用向量的夹角公式求解.
详解:
因为向量,
所以,
所以,
因为,
所以,
故答案为:(或135°)
14-6【基础】 【正确答案】 或2
【试题解析】 分析:
转化为,即得解
详解:
已知,,若,
则,,,,
,,
,
,或,
故答案为:或2.
点睛:
本题考查了向量垂直的坐标表示,考查了学生概念理解,数学运算能力,属于基础题
15-1【基础】 【正确答案】
【试题解析】 分析:
由椭圆得b,c,由此能求面积
详解:
由题,则四边形的面积为
故答案为
点睛:
本题考查椭圆的面积问题,是基础题
15-2【提升】 【正确答案】 9
【试题解析】 分析:
设出p点的坐标(x1,y1),根据PF1⊥PF2,求出y1,再根据 求面积.
详解:
解:椭圆C:1的左、右焦点分别为F1(﹣4,0)、F2(4,0),
设P(x1,y1),由已知PF1⊥PF2,所以 ,
即 (﹣4﹣x1,﹣y1) (4﹣x1,﹣y1)=0,
∴x12+y12=16,
又因为 1,
解得 ,所以,△PF1F2的面积.
故答案为9.
点睛:
本题考查了椭圆的标准方程、椭圆的简单性质以及根据一些性质求面积,用到数形结合思想,这是高中数学的一种重要思想.
15-3【巩固】 【正确答案】 64.
【试题解析】 分析:
根据题目三角形且满足,为椭圆的两个焦点,点在椭圆上,则可利用椭圆的性质,根据完全平方公式和勾股定理可得的值,即可求得三角形的面积.
详解:
由椭圆可得.
为椭圆的两个焦点,点在椭圆上,
可得①,
∵,
∴②,
①式平方可得,
整理得,
∴,
故答案为:64.
点睛:
本题考查椭圆的简单几何性质,利用完全平方公式及直角三角形三边关系,解出直角边之积进而得到三角形面积,属于简单题.
15-4【基础】 【正确答案】 2
【试题解析】 分析:
将椭圆方程化为标准方程,求得,根据焦点坐标与顶点坐标求得三角形面积.
详解:
椭圆方程可化为.
,从而.
因此,两焦点为,短轴的个端点为.
∴构成的三角形的面积为.
故答案为:2.
点睛:
本题主要考查椭圆的简单几何性质,属基础题.
15-5【巩固】 【正确答案】 9
【试题解析】 分析:
根据椭圆的方程求得c,得到|F1F2|,设出|PF1|=t1,|PF2|=t2,利用勾股定理以及椭圆的定义,可求得t1t2的值,即可求出三角形面积.
详解:
∵a=5,b=3;∴c=4,
设|PF1|=t1,|PF2|=t2,
则t1+t2=10①t12+t22=82②,
由①2﹣②得t1t2=18,
∴.
故答案为9.
点睛:
本题主要考查了椭圆的标准方程、椭圆的简单性质.解答的关键是通过勾股定理解三角形,考查计算能力.
15-6【提升】 【正确答案】 3
【试题解析】 分析:
令|F1P|=m、|PF2|=n,由椭圆的定义得 m+n,在Rt△F1PF2中,由勾股定理得m2+n2,从而可得m n的值,即得△F1PF2的面积,从而得到答案.
详解:
令|F1P|=m、|PF2|=n,由椭圆的定义可得 m+n=2a①,
Rt△F1PF2 中,由勾股定理可得(2c)2=m2+n2②,由①②可得mn=2b2,
∴△F1PF2的面积是==9,即b=3,
故答案为3.
点睛:
本题考查三角形面积的计算,考查椭圆的定义,考查勾股定理,考查学生的计算能力,属于基础题.
16-1【巩固】 【正确答案】
【试题解析】 分析:
根据图象可得,由题意得出,即可求出,再代入即可求出,进而得出所求.
详解:
由函数图象可得,
相邻的两条对称轴之间的距离为,,则,,
,
又,即,,或,
根据“五点法”画图可判断,,
.
故答案为:.
16-2【基础】 【正确答案】
【试题解析】 分析:
根据最大值得,再由图像得周期,从而得,根据时,取得最大值,利用整体法代入列式求解,再结合的取值范围可得.
详解:
根据图像的最大值可知,,由,可得,所以,再由得,,所以,因为,所以,故函数的解析式为.
故答案为:.
16-3【提升】 【正确答案】
【试题解析】 分析:
根据函数图象有,可求得,又函数图象过点,点,代入可求得,,求得,然后利用函数的周期性求解.
详解:
由图可知:,,
所以函数,
又函数图象过点,点,,
,
所以,
,
故答案为:
点睛:
方法点睛:求函数解析式的步骤:
(1)求A,B,确定函数的最大值M和最小值m,则,.
(2)求,确定函数的周期,则
(3)求,常用方法如下:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入.
16-4【巩固】 【正确答案】
【试题解析】 分析:
由题意利用函数的图象变换规律,得到的解析式,再根据正弦函数的单调增区间,求得的取值范围.
详解:
解:将函数的图象向左平移个单位,
得到函数 的图象.
若在区间上为增函数,则,且,
求得,则的取值范围为,,
故答案为:,.
16-5【提升】 【正确答案】
【试题解析】 分析:
原问题转化为在区间上至少有2个,至多有3个t,使得,求得取值范围,作出可知,满足条件可最短区间长度为,最长区间长度为,由此建立关于的不等式,解出即可.
详解:
令,则,令,则,
则原问题转化为在区间上至少有2个,至多有3个t,使得,求得取值范围,
作出与的图象,如图所示,
由图可知,满足条件可最短区间长度为,最长区间长度为,
∴,解得.
故答案为:.
16-6【基础】 【正确答案】
【试题解析】 分析:
由正弦函数的图象求得,令利用导数求其最值,由题设不等式恒成立知,结合三角形内角的性质求的取值范围.
详解:
由图知:,,即,可知.
由,得,,
∴,,又,即,
∴.
设,则,
当时,,单调递减,
当时,,单调递增,
∴,即,得.
由,得.
结合正弦函数的图象可知,当时成立,
∴的范围是.
故答案为:
17-1【基础】 【正确答案】 有99%的把握认为该血清能起到预防感冒的作用.
【试题解析】 分析:
利用公式计算得出数据,比较数据大小得解
详解:
解:设H0:感冒与是否使用该血清没有关系.
因当H0成立时,χ2≥6.635的概率约为0.01,故有99%的把握认为该血清能起到预防感冒的作用.
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
17-2【巩固】 【正确答案】 在犯错的概率不超过0.1的前提下可以认为性别与出生时间有关联.
【试题解析】 分析:
根据题目所给的数据,计算,对照参数即可下结论.
详解:
由题意得的观测值为:
,
∴在犯错的概率不超过0.1的前提下可以认为性别与出生时间有关联.
17-3【巩固】 【正确答案】 (1)列联表见解析;有的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;(2)答案见解析.
【试题解析】 分析:
(1)根据已知数据补全列联表,利用公式计算得到,由此可得结论;
(2)根据数据可知个体经营户配合度需提高,由此可确定统计建议.
详解:
(1)根据已知数据,完成列联表如下:
顺利 不顺利 合计
企事业单位 40 10 50
个体经营户 100 50 150
合计 140 60 200
,
有的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”.
(2)建议:加大宣传力度,消除误解因素,尤其要做好个体经营户的思想工作.(意思相近即可)
17-4【提升】 【正确答案】 没有充分证据认为“成绩与班级有关系”.
【试题解析】 分析:
计算出卡方值,即可判断.
详解:
计算得的观测值为,
因为0.653<3.841,所以没有充分证据认为“成绩与班级有关系”.
17-5【基础】 【正确答案】 (1)表格见解析;(2)没有的把握认为参加体育锻炼与否跟性别有关.
【试题解析】 分析:
(1)根据调查结果完成列联表即可;
(2)根据列联表计算,与附表对照,即可判断.
详解:
解:(1)填写的列联表如下
男性居民 女性居民 合计
不参加体育锻炼
参加体育锻炼
合计
(2)计算
因为.
所以没有的把握认为参加体育锻炼与否跟性别有关.
点睛:
本题考查了利用独立性检验解决实际问题,属于基础题.
17-6【提升】 【正确答案】 (1)答案见解析;(2),没有90%的把握认为“成绩与班级有关”.
【试题解析】 分析:
(1)根据条形图中数据完成表格即可;
(2)根据公式计算出的值,然后可得答案.
详解:
(1)根据条形图中的数据可得如下表格,
甲班 乙班 总计
优秀 15 20 35
非优秀 40 30 70
总计 55 50 105
(2)
因为,所以没有90%的把握认为“成绩与班级有关”.
点睛:
本题考查的是独立性检验,考查了学生的计算能力,属于基础题.
18-1【基础】 【正确答案】 选①和②得结果相同,(1);(2)
【试题解析】 分析:
(1)选①②直接根据数列的递推关系式求出公比,从而可求得数列的通项公式;
(2)直接利用(1)的结论,进一步利用分组求和法求出数列的前项和.
详解:
解:(1)选条件①
设数列的公比为,由得,
∴即或;又数列是正项数列,故.
从而数列的通项公式为:.
选条件②
设数列的公比为,由,,成等差数列,∴,
所以,解得,
从而数列的通项公式为:.
(2),
.
18-2【巩固】 【正确答案】 选①②③结果均相同,(Ⅰ);(Ⅱ)见解析;(Ⅲ)
【试题解析】 分析:
分别选①②③,(Ⅰ)由数列的递推式或等差数列的定义和性质,可得公差,通项公式;
(Ⅱ)由等比数列的定义,可得证明;
(Ⅲ)求得,由数列的分组求和,结合等差数列和等比数列的求和公式,可得所求和.
详解:
解:选①,(Ⅰ)因为,时,,
则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
.
选②,(Ⅰ)由,,则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
.
选③,(Ⅰ)由,且,
可得数列为等差数列,设公差为,
则,
则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
所以
.
18-3【提升】 【正确答案】 (1);(2)答案不唯一,具体见解析.
【试题解析】 分析:
(1)设等差数列的首项为,公差为d,解方程组即得数列的通项公式及;(2)选①:利用错位相减法求和得解;选②:利用裂项相消法求和得解;选③:对分两种情况讨论求和得解.
详解:
(1)设等差数列的首项为,公差为d,
,所以,
.
(2)选①:
①
②
由①-②得,
选②:,
所以,
所以
选③:
当n为偶数时,
当n为奇数时,
所以.
18-4【巩固】 【正确答案】 (1),;(2).
【试题解析】 分析:
(1)根据题中条件求解数列的基本参数进而求解出数列的通项公式;
(2)先求解数列的前n项和,结合不等式恒成立问题求解出参数的范围.
详解:
(1)时,
时,
n=1时,,∴.
由得,
∵,∴,所以,
∴,;
(2),
,
,;令,
,∴,
∴,∴实数的取值范围为.
18-5【提升】 【正确答案】 (1)若选①,,若选②,,若选③,;(2)若选①,
,若选②, ,若选③, .
【试题解析】 分析:
(1)根据,,成等比数列,用等差数列的基本量进行运算,可得首项和公差的关系,结合条件即可得到答案;
(2)由(1)解出的通项公式,进而根据分组求和即可得到答案.
详解:
(1)设数列的公差为.因为,,成等比数列,则,
故,化简得.因为,所以,所以.
若选①,则,即,则;
若选②,则,即,则;
若选③,则,即,则;
(2)因为数列是各项均为正数的等比数列,且,,
设数列的公比为,则.
若选①,则,故,,
所以,由,得.又,则,所以,
所以.
若选②,则,故,,
所以,由,得.又,则,所以,
所以.
若选③,则,故,,
所以,由,得.又,则,所以,
则.
18-6【基础】 【正确答案】 (1);(2)答案见解析.
【试题解析】 分析:
(1)根据求解即可;
(2)选①利用错位相减法求和即可;选②利用裂项相消法求和即可;选③对分奇偶讨论,然后利用并项求和法求和即可.
详解:
(1)∵在数列中,.
当时,,
当时,,
又也满足,
∴
(2)选择条件①,
∴①
②
①-②得
故.
选择条件②由(1)知:,
∴
∴
选择条件③
,
∴当为偶数时,
当为奇数时,
综上所述:.
19-1【基础】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)由侧面PAB⊥平面PBC,可得BC⊥侧面PAB,所以PA⊥BC,再由PD=DB=DA,所以PA⊥AB,利用线面垂直的判定定理即得证;
(2)建立空间直角坐标系,求出两个平面的法向量,利用二面角的向量计算公式,即得解.
详解:
(1)侧面PAB⊥平面PBC,PB⊥BC,所以BC⊥侧面PAB
又PA侧面PAB,所以PA⊥BC
又PD=DB=DA,可得,
又内角和为
所以PA⊥AB
又ABBC=B,所以PA⊥平面ABC
(2)以A为原点,过点A作BC的平行线为x轴,AB,AP所在直线分别y z轴,建立空间直角坐标系,如图所示.
在直角三角形PAB中,,由已知得:.
,
设平面ACD的法向量为,
则,即,取,则,
故
设平面ABD的法向量为,
又二面角A-PD-C为锐角,故二面角A-PD-C的余弦值为
故答案为:.
点睛:
本题考查了面面垂直的性质,线面垂直的判定,以及向量法求二面角,考查了学生综合分析,逻辑推理,数学运算的能力,属于中档题
19-2【巩固】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)由已知中,四棱柱的所有棱长都相等,,,四边形和四边形均为矩形.可得且,,进而,,再由线面垂直的判定定理得到底面;
(2)设四棱柱的所有棱长均为,设为2,若,,,以为坐标原点,分别以,,为,,轴正方向建立空间直角坐标系,求出平面和平面的法向量,代入向量夹角公式,求出二面角的余弦值.
详解:
证明:(1)四棱柱的所有棱长都相等,
四边形为菱形,
又,
故为的中点,
同理也是的中点,
又四边形和四边形均为矩形,
且,,
,,
又,,平面,
底面;
解:(2)设四棱柱的所有棱长均相等,所以四边形是菱形,
,
又底面,
,,两两垂直,
如图,以为坐标原点,,,所在直线分别为轴,轴,轴建立直角坐标系.
设,
,
,,
则,,,
易知,是平面的一个法向量,
设,,是平面的一个法向量,则,即
取,则,,所以,,
设二面角的大小为,易知是锐角,于是:
,
故二面角的余弦值为.
19-3【提升】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)设,利用勾股定理逆定理可得,再根据面面垂直的性质证明即可;
(2)建立如图所示空间直角坐标系,利用空间向量法求出二面角的余弦值;
详解:
解:(1)设,则,
∴,∴.
∵平面平面,平面平面,
∴平面.
(2)取中点O,连接,
∵,∴,∴平面,
建立如图所示空间直角坐标系,设,则,
,
设平面的法向量为,则,取可得,
设平面的法向量为,则,取可得,
所以,
由图可得二面角为钝角,∴二面角的余弦值为.
19-4【提升】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)根据题意证明平面可得,再结合即可证明平面;
(2)结合(1),以,,所在直线分别为轴,轴和轴,建立空间直角坐标系,利用坐标法求解即可.
详解:
解:(1)证明:∵在菱形ABCD中,∠BAD=60,DEAB于点E
∴,,∴.
又∵,,
∴平面,∴.
又∵,,
∴平面.
(2)∵平面,,
∴以,,所在直线分别为轴,轴和轴,建立空间直角坐标系(如图).
易知,则,,,,
∴,,
易知平面的一个法向量为.
设平面的法向量为,
由,,得,令,得,
∴.
由图得二面角为钝二面角,
∴二面角的余弦值为.
19-5【基础】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)证明,,则平面即得证;
(2)取中点为E,连结,,证明平面,以E为坐标原点,,,分别为x,y,z轴,建立空间直角坐标系,利用向量法求解即可.
详解:
(1)由,则有,又D为的中点,所以,
由,则有,,
又,
所以,
则可知,
又有,平面,所以平面;
(2)取中点为E,连结,,
由,则有,
又易知,
则有,所以,
又可知,,平面,则平面,
如图,以E为坐标原点,,,分别为x,y,z轴,建立空间直角坐标系,
有,,,,,
由,则有平面,
所以,
又,,
所以平面,
所以平面的法向量为,
设平面的法向量为,
则有,即,
可取,
记二面角为,
则.
故二面角的余弦值为.
19-6【巩固】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)连接交于点O,连接、,先证明平面,再由三角形中位线定理得到,即可证明平面.
(2)以分别为x轴,y轴,z轴正方向建立空间直角坐标系,设,用向量法求二面角的余弦值.
详解:
(1)连接交于点O,连接、,
因为为等边三角形,所以,
因为底面为正方形,所以,
因为,所以平面,
又平面,所以,
因为平面平面,平面平面,
所以平面,
因为E为中点,所以,则平面.
(2)如图,以分别为x轴,y轴,z轴正方向建立空间直角坐标系,设,则,
所以,,,,
则,,,
因为平面平面,且平面平面=BD,,
所以面EBD,
所以平面的法向量为,
设平面的法向量为,则,
所以,不妨设x=1,所以,
所以,
显然二面角的平面角为锐角或直角,
所以二面角的余弦值为.
20-1【提升】 【正确答案】 (1);(2)证明见解析.
【试题解析】 分析:
(1)求得交点坐标为,利用两点之间的距离公式即可得解;
(2)由直线与抛物线联立可求得,,结合已知条件可知,利用点斜式可知直线的方程为,即可证得结论.
详解:
(1)联立,得,即交点坐标为,
所以,,
抛物线的标准方程为
(2)证明:设,,
将代入抛物线方程得,所以,.
设直线,同理,,
因为与直线关于直线对称,由图形对称性,计算可得.
所以,,
又,
所以直线的方程为,
化简有,所以恒过定.
点睛:
思路点睛:解决直线与抛物线的综合问题时,要注意:
(1)注意观察应用题设中的每一个条件,明确确定直线、抛物线的条件;
(2)强化有关直线与抛物线联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.
20-2【巩固】 【正确答案】 (1);(2)①;②.
【试题解析】 分析:
(1)可设出点的坐标,由直线,过作直线的垂线,垂足为点,则,则我们根据,构造出一个关于,的方程,化简后,即可得到所求曲线的方程;
(2)①由过点的直线交轨迹于、两点,交直线于点,我们可以设出直线的点斜式方程,联立直线方程后,利用设而不求的思想,结合一元二次方程根与系数关系,易求的值.
②根据平面向量数量积的性质,结合基本不等式进行求解即可.
详解:
(1)设点,则,由,
得, 化简得曲线的方程为;
(2)由于直线不能垂直于轴,且又过轴上的定点,
设直线的方程为,则 ,
设,,联立方程组
消去得,,故
由,,得
利用对应的纵坐标相等,得,,整理得,,
所以.
②因为,,所以有:由上可知: ,
因此有,
所以,当且仅当时取等号,即当时取等号,
因此.
点睛:
关键点睛:结合基本不等式,利用平面向量数量积的运算性质是解题的关键.
20-3【提升】 【正确答案】 (1);(2)存在
【试题解析】 分析:
(1)根据焦距和椭圆的几何意义即可求出椭
【原卷 1 题】 知识点 并集,交集
【正确答案】 B
【试题解析】
1-1【基础】 已知集合M={x|﹣4<x≤2},N={x|y=},则M∩N=( )
A.{2} B.{x|﹣4<x≤﹣2}
C.{x|﹣4<x≤2} D.{x|﹣2≤x≤2}
【正确答案】 B
1-2【巩固】 设集合,,则( )
A. B. C. D.
【正确答案】 A
1-3【巩固】 已知集合P={x∈N|x≤3},Q={x|x2≤x+2},则P∩Q=( )
A.{﹣1,0,1,2} B.[0,2] C.{0,1,2} D.{1,2}
【正确答案】 C
1-4【基础】 设集合,集合,则集合=
A. B. C. D.
【正确答案】 A
1-5【提升】 已知集合,,则( )
A. B. C. D.
【正确答案】 A
1-6【提升】 集合,,求( )
A. B. C. D.
【正确答案】 A
【原卷 2 题】 知识点 频率分布直方图,平均数
【正确答案】 C
【试题解析】
2-1【基础】 爱美之心,人皆有之.健身减肥已成为很多肥胖者业余选择的项目.为了了解运动健身减肥的效果,某健身房调查了40名肥胖者,健身之前他们的体重(单位:)情况如柱状图1所示,经过四个月的健身后,他们的体重情况如柱状图2所示.对比健身前后,关于这40名肥胖者,下面结论不正确的是( )
A.他们健身后,体重在区间内的人数增加了4个
B.他们健身后,体重在区间内的人数没有改变
C.因为体重在内所占比例没有发生变化,所以说明健身对体重没有任何影响
D.他们健身后,原来体重在区间内的肥胖者体重都有减少
【正确答案】 C
2-2【巩固】 供电部门对某社区1000位居民2019年4月份人均用电情况进行统计后,按人均用电量分为,,,五组,整理得到如下的频率分布直方图,则下列说法错误的是
A.4月份人均用电量人数最多的一组有400人
B.4月份人均用电量不低于20度的有500人
C.4月份人均用电量为25度
D.在这1000位居民中任选1位协助收费,选到的居民用电量在一组的概率为
【正确答案】 C
2-3【提升】 下面是追踪调查200个某种电子元件寿命(单位:)频率分布直方图,如图:
其中300-400、400-500两组数据丢失,下面四个说法中有且只有一个与原数据相符,这个说法是
①寿命在300-400的频数是90;
②寿命在400-500的矩形的面积是0.2;
③用频率分布直方图估计电子元件的平均寿命为:
④寿命超过的频率为0.3
A.① B.② C.③ D.④
【正确答案】 B
2-4【巩固】 在2019年某省普通高中学业水平考试(合格考)中,对全省所有考生的物成绩进行统计,可得到如图所示的频率分布直方图,其中分组的区间为,,,,,90分以上为优秀,则下列说法中不正确的是( )
A.从全体考生中随机抽取1000人,则其中得优秀考试约有100人
B.若要全省的合格考通过率达到,则合格分数线约为44分
C.若同一组中数据用该组区间中间值作代表值,可得考试物理成绩的平均分约为70
D.该省考生物理成绩的中位数为75分
【正确答案】 D
2-5【提升】 2021年4月8日,教育部办公厅“关于进一步加强中小学生体质健康管理工作的通知”中指出,各地要加强对学生体质健康重要性的宣传,中小学校要通过体育与健康课程、大课间、课外体育锻炼、体育竞赛、班团队活动、家校协同联动等多种形式加强教育引导,让家长和中小学生科学认识体质健康的影响因素.了解运动在增强体质、促进健康、预防肥胖与近视、锤炼意志、健全人格等方面的重要作用,提高学生体育与健康素养.增强体质健康管理的意识和能力.某高中学校共有2000名男生,为了了解这部分学生的身体发育情况,学校抽查了100 名男生的体重情况.根据所得数据绘制样本的频率分布直方图如图所示.根据此图,下列说法中错误的是( )
A.样本的众数约为
B.样本的中位数约为
C.样本的平均值约为66
D.为确保学生体质健康,学校将对体重超过的学生进行健康监测,该校男生中需要监测的学生频数约为200人
【正确答案】 C
2-6【基础】 某校为了解学生体能素质,随机抽取了50名学生,进行体能测试,并将这50名学生成绩整理得如下频率分布直方图.根据此频率分布直方图,下列结论中不正确的是( )
A.这50名学生中成绩在[80,100]内的人数有10人
B.这50名学生中成绩在[40,60)内的人数占比为28%
C.这50名学生成绩的中位数为70
D.这50名学生的平均成绩(同一组中的数据用该组区间的中点值做代表)
【正确答案】 C
【原卷 3 题】 知识点 复数的乘除和乘方
【正确答案】 B
【试题解析】
3-1【提升】 若,则( )
A.0 B.1
C. D.2
【正确答案】 C
3-2【基础】 若复数满足,其中是虚数单位,则( )
A. B. C. D.
【正确答案】 A
3-3【提升】 已知复数满足,则( )
A. B. C. D.
【正确答案】 A
3-4【基础】 已知复数满足,则( )
A. B. C. D.
【正确答案】 B
3-5【巩固】 在复平面内,复数满足,则( )
A. B. C. D.
【正确答案】 D
3-6【巩固】 设,则( )
A. B. C. D.
【正确答案】 A
【原卷 4 题】 知识点 对数的运算,对数函数的概念,对数的概念
【正确答案】 C
【试题解析】
4-1【基础】 某科技股份有限公司为激励创新,计划逐年增加研发资金投入.若该公司2020年全年投入的研发资金为100万元,在此基础上,每年投入的研发资金比上一年增长,则该公司全年投入的研发资金开始超过140万元的年份是参考数据:,( )
A.2025年 B.2026年 C.2027年 D.2028年
【正确答案】 B
4-2【巩固】 声强级(单位:)由公式给出,其中为声强(单位:).某班级为规范同学在公共场所说话的文明礼仪,开展了“不敢高声语,恐惊读书人”主题活动,要求课下同学之间交流时,每人的声强级不超过40.现有4位同学课间交流时,声强分别为,,,,则这4人中达到班级要求的有( )
A.1人 B.2人 C.3人 D.4人
【正确答案】 C
4-3【基础】 某工厂产生的废气必须经过过滤后排放,规定排放时污染物的残留含量不得超过原污染物总量的0.5%.已知在过滤过程中的污染物的残留数量P(单位:毫克/升)与过滤时间t(单位:小时)之间的函数关系为(为原污染物总量).要能够按规定排放废气,则需要过滤n小时,则正整数n的最小值为(参考数据:取)( )
A.13 B.14 C.15 D.16
【正确答案】 D
4-4【提升】 为了保证信息安全传输,有一种称为秘密密钥密码系统,其加密 解密原理如图:,现在加密密钥为,解密密钥为,如下所示:发送方发送明文“1”,通过加密后得到密文“18”,再发送密文“18”,接受方通过解密密钥解密得明文“49”,问若接受方接到明文“4”,则发送方发送明文为( )
A. B. C.162 D.
【正确答案】 A
4-5【巩固】 我们知道:人们对声音有不同的感觉,这与它的强度有关系.一般的,声音的强度用()表示,但在实际测量时,声音的强度水平常用(单位:分贝,,其中是人们平均能听到的最小强度,是听觉的开端).某新建的小区规定:小区内公共场所的声音的强度水平必须保持在50分贝以下,则声音强度的取值范围是( )
A. B. C. D.
【正确答案】 C
4-6【提升】 香农定理是所有通信制式最基本的原理,它可以用香农公式来表示,其中是信道支持的最大速度或者叫信道容量,是信道的带宽(),S是平均信号功率(),是平均噪声功率().已知平均信号功率为,平均噪声功率为,在不改变平均信号功率和信道带宽的前提下,要使信道容量增大到原来的2倍,则平均噪声功率约降为( )
A. B. C. D.
【正确答案】 A
【原卷 5 题】 知识点 双曲线的定义,双曲线的离心率,余弦定理
【正确答案】 A
【试题解析】
5-1【提升】 分别是双曲线的左、右焦点,过的直线分别交该双曲线的左、右两支于A、B两点,若,则( )
A.2 B. C.4 D.
【正确答案】 C
5-2【提升】 已知双曲线(,)的左右焦点,,过的直线交右支于、两点,若,,则该双曲线的离心率为( )
A. B.2 C. D.
【正确答案】 B
5-3【巩固】 已知分别是双曲线的两个焦点,双曲线和圆的一个交点为,且,那么双曲线的离心率为( )
A. B. C.2 D.
【正确答案】 D
5-4【巩固】 设为双曲线:的左焦点,为坐标原点,以为圆心,为半径的圆与交于两点.若,则的离心率为( )
A. B. C. D.
【正确答案】 A
5-5【基础】 已知双曲线与函数的图象交于点,若函数的图象在点处的切线过双曲线左焦点,则双曲线的离心率是( )
A. B. C. D.
【正确答案】 D
5-6【基础】 已知双曲线:的左、右焦点分别为,,点在的右支上,直线与的左支交于点,若,且,则的离心率为( )
A. B. C. D.
【正确答案】 D
【原卷 6 题】 知识点 画几何体的三视图,三视图
【正确答案】 D
【试题解析】
6-1【巩固】 在空间直角坐标系中,一个四面体的顶点坐标分别为,,,.画该四面体三视图中的正视图时,以平面为投影面,则得到正视图可以为( ).
A. B. C. D.
【正确答案】 A
6-2【基础】 一个锥体的正视图和侧视图如图所示,下面选项中,不可能是该锥体的俯视图的是
A. B. C. D.
【正确答案】 C
6-3【提升】 将正三棱柱截去三个角(如图1所示A,B,C分别是△CHI三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为
A. B. C. D.
【正确答案】 A
6-4【提升】 如图所示的几何体各自的三视图中,有且仅有两个视图相同的为
A.①② B.②④
C.①④ D.①③
【正确答案】 B
6-5【基础】 在如图所示的空间直角坐标系中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为
A.①和② B.③和① C.④和③ D.④和②
【正确答案】 D
6-6【巩固】 如下图,在正方体中,点是棱上一点,则三棱锥的侧视图是
A. B. C. D.
【正确答案】 D
【原卷 7 题】 知识点 必要不充分条件,递增数列与递减数列
【正确答案】 B
【试题解析】
7-1【提升】 设无穷等比数列{an}的前n项和为Sn若-a1<a2<a1,则( )
A.{Sn}为递减数列 B.{Sn}为递增数列
C.数列{Sn}有最大项 D.数列{Sn}有最小项
【正确答案】 D
7-2【巩固】 已知数列{an}满足a1=2,2anan+1= +1,设bn=,则数列{bn}是( )
A.常数列 B.摆动数列
C.递增数列 D.递减数列
【正确答案】 D
7-3【巩固】 已知数列满足,其中且,则下列说法正确的是( )
A.当时,存在一个实数和正整数,使得,,成等差数列
B.当时,存在一个实数和正整数,使得,,成等差数列
C.当时,数列是递增的
D.当时,数列是递减的
【正确答案】 D
7-4【提升】 已知数列满足,,则下列选项中正确的是( )
A. A当且仅当时,数列为递增数列
B. B.存在实数和正整数,,使得
C. C.当且仅当时,数列为递减数列
D. D当时,数列,均为递增数列
【正确答案】 D
7-5【基础】 已知数列的项都是实数,则对于一切,“数列为递减数列”是“”的( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.不充分也不必要条件
【正确答案】 B
7-6【基础】 在等比数列{an}中,“a2>a1”是“{an}为递增数列”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要
【正确答案】 B
【原卷 8 题】 知识点 两角和与差的正弦公式,正弦定理
【正确答案】 B
【试题解析】
8-1【基础】 雕塑成了大学环境不可分割的一部分,有些甚至能成为这个大学的象征,在中国科学技术大学校园中就有一座郭沫若的雕像.雕像由像体和底座两部分组成.如图,在中,,在中,,且米,求像体的高度( )(最后结果精确到0.1米,参考数据:,,)
A.4.0米 B.4.2米 C.4.3米 D.4.4米
【正确答案】 B
8-2【基础】 为了测量西藏被誉称为“阿里之巅”冈仁波齐山峰的高度,通常采用人工攀登的方式进行,测量人员从山脚开始,直到到达山顶分段测量,最后将所有的高度差累加,得到珠峰的高度,在测量过程中,已知竖立在点处的测量觇标高米,攀登者们在处测得到觇标底点和顶点的仰角分别为,,则、的高度差约为( )
(参考数据:,,)
A.米 B.米
C.米 D.米
【正确答案】 C
8-3【巩固】 “欲穷千里目,更上一层楼”出自唐朝诗人王之涣的《登鹳雀楼》,鹳雀楼位于今山西永济市,该楼有三层,前对中条山,下临黄河,传说常有鹳雀在此停留,故有此名.下面是复建的鹳雀楼的示意图,某位游客(身高忽略不计)从地面点看楼顶点的仰角为30°,沿直线前进79米到达点,此时看点的仰角为45°,若,则楼高约为( ).
A.65米 B.74米 C.83米 D.92米
【正确答案】 B
8-4【巩固】 圣·索菲亚教堂(英语:SAINT SOPHIA CATHEDRAL)坐落于中国黑龙江省,是一座始建于1907年拜占庭风格的东正教教堂,距今已有114年的历史,为哈尔滨的标志性建筑.1996年经国务院批准,被列为第四批全国重点文物保护单位,是每一位到哈尔滨旅游的游客拍照打卡的必到景点其中央主体建筑集球,圆柱,棱柱于一体,极具对称之美,可以让游客从任何角度都能领略它的美.小明同学为了估算索菲亚教堂的高度,在索菲亚教堂的正东方向找到一座建筑物,高为,在它们之间的地面上的点(三点共线)处测得楼顶,教堂顶的仰角分别是和,在楼顶处测得塔顶的仰角为,则小明估算索菲亚教堂的高度为( )
A. B. C. D.
【正确答案】 D
8-5【提升】 魏晋时刘徽撰写的《海岛算经》是有关测量的数学著作,其中第一题是测海岛的高.如图,点,,在水平线上,和是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,称为“表距”,和都称为“表目距”,与的差称为“表目距的差”则海岛的高( )
A.表高 B.表高
C.表距 D.表距
【正确答案】 A
8-6【提升】 如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°,从C点测得∠MCA=60°,已知山高BC=100 m,则山高MN=( )
A.150m B.180m C.120m D.160m
【正确答案】 A
【原卷 9 题】 知识点 已知正(余)弦求余(正)弦,由条件等式求正、余弦,已知弦(切)求切(弦),同角三角函数的基本关系,二倍角的正弦公式,二倍角的余弦公式
【正确答案】 A
【试题解析】
9-1【巩固】 已知,(0, π),则=
A.1 B. C. D.1
【正确答案】 A
9-2【提升】 已知,则( )
A. B. C. D.
【正确答案】 C
9-3【基础】 已知,,则( )
A. B. C. D.
【正确答案】 D
9-4【巩固】 若,是第三象限角,则( )
A. B. C. D.
【正确答案】 A
9-5【提升】 若,则( )
A. B. C. D.
【正确答案】 C
9-6【基础】 已知,且,则
A.2 B. C.3 D.
【正确答案】 A
【原卷 10 题】 知识点 排列应用题,古典概型的概率计算公式
【正确答案】 C
【试题解析】
10-1【基础】 从包括甲 乙在内的7名学生中选派4名学生排序参加演讲比赛,则甲和乙参加,且演讲顺序不相邻的概率为( )
A. B. C. D.
【正确答案】 B
10-2【提升】 从分别写有的张卡片中随机抽取张,放回后再随机抽取张,则抽得的第一张卡片上的数大于第二张卡片上的数的概率为
A. B. C. D.
【正确答案】 D
10-3【基础】 生物实验室有5只兔子,其中只有3只测量过某项指标,若从这5只兔子中随机取出3只,则恰有2只测量过该指标的概率为
A. B. C. D.
【正确答案】 B
10-4【提升】 如图为我国数学家赵爽约3世纪初在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则区域涂色不相同的概率为
A. B. C. D.
【正确答案】 D
10-5【基础】 我国古代典籍《周易》用“卦”描述万物的变化.每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“— —”,如图就是一重卦.在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是
A. B. C. D.
【正确答案】 A
10-6【基础】 6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有( )
A.120种 B.90种
C.60种 D.30种
【正确答案】 C
【原卷 11 题】 知识点 球,柱、锥、台的体积,组合体的表面积和体积
【正确答案】 A
【试题解析】
11-1【巩固】 已知矩形的顶点都在半径为5的球的球面上,且,,则棱锥的体积为( )
A. B. C. D.
【正确答案】 C
11-2【基础】 已知,,三点均在球的表面上,,且球心到平面的距离为2,则球的内接正方体的棱长为( )
A.1 B. C.2 D.
【正确答案】 D
11-3【提升】 已知在中,角所对的边分别为,且又点都在球的球面上,且点到平面的距离为,则球的体积为( )
A. B. C. D.
【正确答案】 C
11-4【巩固】 一个球面上有三个点、、,若,,球心到平面的距离为1,则球的表面积为( )
A. B. C. D.
【正确答案】 D
11-5【提升】 已知是面积为的等边三角形,且其顶点都在球的球面上,若球的体积为,则到平面的距离为( )
A. B. C.1 D.
【正确答案】 C
11-6【基础】 平面截球所得截面圆的面积为,球心到平面的距离为,则此球的表面积为( )
A. B. C. D.
【正确答案】 D
【原卷 12 题】 知识点 函数的奇偶性,函数的周期性
【正确答案】 D
【试题解析】
12-1【巩固】 已知函数在定义域上单调,且,则的值为( )
A.3 B.1 C.0 D.﹣1
【正确答案】 A
12-2【基础】 已知函数是R上的偶函数.若对于都有,且当时,,则的值为( )
A.﹣2 B.﹣1 C.1 D.2
【正确答案】 C
12-3【巩固】 函数是上的奇函数,满足,当时,有,求的值( )
A.0 B.1 C. D.
【正确答案】 A
12-4【基础】 已知函数是定义域为R的奇函数,周期为2,且当时,,则 等于( )
A. B. C. D.
【正确答案】 B
12-5【提升】 已知函数满足,若在上为偶函数,且其解析式为,则的值为
A. 1 B.0
C. D.
【正确答案】 B
12-6【提升】 已知函数的定义域为,且函数的图象关于轴对称,函数的图象关于原点对称,则
A. B. C. D.
【正确答案】 A
【原卷 13 题】 知识点 导数的几何意义
【正确答案】 5x-y+2=0
【试题解析】
13-1【提升】 曲线在点处的切线与两坐标轴所围成的三角形的面积为_______.
【正确答案】
13-2【基础】 曲线在点处的切线的横纵截距之和为__________.
【正确答案】
13-3【巩固】 在平面直角坐标系中,曲线在处的切线方程是___________.
【正确答案】
13-4【提升】 已知为奇函数,当时,,则曲线在处的切线方程是_________.
【正确答案】
13-5【基础】 函数的图象在点处的切线方程为__________.
【正确答案】
13-6【巩固】 函数f(x)=lnx+x的图象在x=1处的切线方程为___.
【正确答案】 2x﹣y﹣1=0
【原卷 14 题】 知识点 正弦函数的定义域、值域和最值,平面向量的数量积,数量积的坐标表示
【正确答案】
【试题解析】
14-1【巩固】 已知向量,,,则__________.
【正确答案】
14-2【提升】 设,,.若,则实数的值等于___________.
【正确答案】
14-3【提升】 设,向量,,,且,,则_________.
【正确答案】
14-4【基础】 已知向量,若向量与垂直,则m=________..
【正确答案】
14-5【巩固】 已知平面向量,则的夹角为________.
【正确答案】 (或135°)
14-6【基础】 已知,,若,则的值是______.
【正确答案】 或2
【原卷 15 题】 知识点 椭圆的弦长、焦点弦
【正确答案】 8
【试题解析】
15-1【基础】 已知椭圆左、右焦点为,,上、下顶点为,,则四边形的面积为______.
【正确答案】
15-2【提升】 设P是椭圆=1上的一点,且,则△PF1F2的面积为_________.
【正确答案】 9
15-3【巩固】 为椭圆的两个焦点,点在椭圆上,且满足,则三角形的面积为_____________________;
【正确答案】 64.
15-4【基础】 椭圆的两个焦点与短轴的一个端点构成的三角形的面积等于________.
【正确答案】 2
15-5【巩固】 .已知、是椭圆的两个焦点,为椭圆上一点,且,则的面积 .
【正确答案】 9
15-6【提升】 已知为椭圆C: (a>b>0)上一点,若,则_____________.
【正确答案】 3
【原卷 16 题】 知识点 三角函数图象的综合应用,余弦函数的单调性,正(余)弦型三角函数的图象
【正确答案】 2
【试题解析】
16-1【巩固】 函数的图象与轴相交于点,如图是它的部分图象,若函数图象相邻的两条对称轴之间的距离为,则_________.
【正确答案】
16-2【基础】 已知函数的图象如图所示,则函数的解析式为__________.
【正确答案】
16-3【提升】 已知,若函数的图像如图所示,则_________
【正确答案】
16-4【巩固】 将函数的图象向左平移个单位,得到函数的图象,若函数在上为增函数,则的取值范围是___________.
【正确答案】
16-5【提升】 设函数,若对于任意实数,在区间上至少有2个零点,至多有3个零点,则的取值范围是________.
【正确答案】
16-6【基础】 已知函数的部分图象如图所示,是某个三角形的内角,若关于的不等式在上恒成立,则的取值范围为______.
【正确答案】
【原卷 17 题】 知识点 独立性检验
【正确答案】 (1)75%;60%;(2)能.
【试题解析】
17-1【基础】 在500人身上试验某种血清预防感冒作用,把他们一年中的感冒记录与另外500名未用血清的人的感冒记录作比较,结果如表所示.问:该种血清能否起到预防感冒的作用?
未感冒 感冒 合计
使用血清 258 242 500
未使用血清 216 284 500
合计 474 526 1000
【正确答案】 有99%的把握认为该血清能起到预防感冒的作用.
17-2【巩固】 调查某医院一段时间内婴儿出生的时间和性别的关联性,得到如下的列联表:
单位:人
性别 出生时间 合计
晚上 白天
女 24 31 55
男 8 26 34
合计 32 57 89
依据的独立性检验,能否认为性别与出生时间有关联?解释所得结论的实际含义.
【正确答案】 在犯错的概率不超过0.1的前提下可以认为性别与出生时间有关联.
17-3【巩固】 为了保障全国第四次经济普查顺利进行,国家统计局选择了江苏、河北、湖北、宁夏、重庆作为国家综合试点地区,逐级进行普查.在普查过程中首先要进行宣传培训,然后确定对象,最后入户登记.由于种种情况可能会导致人户登记不够顺利,这为正式普查提供了宝贵的试点经验.某普查小区,共有50家企事业单位,150家个体经营户,普查情况如下表所示:
顺利 不顺利 合计
企事业单位 40 50
个体经营户 50 150
合计
(1)补全列联表,并根据列联表判断是否有90%的把握认为“此普查小区的人户登记是否顺利与普查对象的类别有关”;
(2)根据该试点普查小区的情况,为保障第四次经济普查的顺利进行,请你从统计的角度提出一条建议.
【正确答案】 (1)列联表见解析;有的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;(2)答案见解析.
17-4【提升】 有甲、乙两个班级进行一门考试,按照学生考试成绩优秀和不优秀统计后,得到如下的列联表:
班级与成绩列联表:
优秀 不优秀 总计
甲班 10 35 45
乙班 7 38 45
总计 17 73 90
试问能有多大把握认为“成绩与班级有关系”?
参考公式及数据:,其中.
0.05 0.01 0.005 0.001
3.841 6.635 7.879 10.828
【正确答案】 没有充分证据认为“成绩与班级有关系”.
17-5【基础】 某杜区为了解居民参加体育锻炼的情况,从该社区中随机抽取了18名男性居民和12名女性居民,对他们参加体育锻炼的情况进行问卷调查.现按是否参加体育锻炼将居民分成两类:甲类(不参加体育锻炼)、乙类(参加体育锻炼),调查结果如下表:
(1)根据上表中的统计数据,完成下面的2 ×2列联表:
(2)通过计算判断是否有95%的把握认为参加体育锻炼与否跟性别有关
附
【正确答案】 (1)表格见解析;(2)没有的把握认为参加体育锻炼与否跟性别有关.
17-6【提升】 某中学高二甲、乙两个兴趣班进行了一次数学对抗赛,该对抗赛试题满分为150分,规定:成绩不小于135分为“优秀”,成绩小于135分为“非优秀”,对这两个班的所有学生的数学成绩统计后,得到如图条形图.
(1)根据图中数据,完成如下的2×2列联表;
甲班 乙班 总计
优秀
非优秀
总计
(2)计算随机变量的值(精确到0.001),并由此判断:能否有90%的把握认为“成绩与班级有关”?
参考数据:
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
参考公式:,其中
【正确答案】 (1)答案见解析;(2),没有90%的把握认为“成绩与班级有关”.
【原卷 18 题】 知识点 数列求和,等差数列及其通项公式,等比数列的通项公式,an与Sn的关系——等差数列
【正确答案】 答案见解析
【试题解析】
18-1【基础】 已知正项等比数列的前项和为,,且________,从下列二个条件:
①; ②,,成等差数列;
中选择一个条件(填上序号),解决下列问题:
(1)求数列的通项公式;
(2)设数列满足,求数列的前项和.
【正确答案】 选①和②得结果相同,(1);(2)
18-2【巩固】 已知数列中,,_____,其中.
(Ⅰ)求数列的通项公式;
(Ⅱ)设,求证:数列是等比数列;
(Ⅲ)求数列的前项和.
从①前项和,①,②,③且,这三个条件中任选一个,补充在上面的问题中并作答.
【正确答案】 选①②③结果均相同,(Ⅰ);(Ⅱ)见解析;(Ⅲ)
18-3【提升】 设等差数列的前n项和为.
(1)求数列的通项公式及;
(2)若 ,求数列的前n项和.
在①;②;③这三个条件中任选一个补充在第(2)问中,并对其求解.
(注意:如果选择多个条件分别解答,按第一个解答计分.)
【正确答案】 (1);(2)答案不唯一,具体见解析.
18-4【巩固】 设数列的前项和为,,是等差数列,,公差,且,,成等比数列.
(1)求数列和的通项公式;
(2)设,数列的前项和为.若对任意的,恒成立,求实数的取值范围.
【正确答案】 (1),;(2).
18-5【提升】 在①,②,③这三个条件中任选一个,补充在下面问题中并作答.
已知是公差不为的等差数列,其前项和为,___________且 成等比数列.
(1)求数列的通项公式;
(2)设数列是各项均为正数的等比数列,且,,求数列的前项和.
【正确答案】 (1)若选①,,若选②,,若选③,;(2)若选①,
,若选②, ,若选③, .
18-6【基础】 已知数列的前项和满足.
(1)求;
(2)已知__________,求数列的前项和.
从下列三个条件中任选一个,补充在上面问题的横线中,然后对第(2)问进行解答.
条件:①
②
③
注:如果选择多个条件分别解答,以第一个解答计分.
【正确答案】 (1);(2)答案见解析.
【原卷 19 题】 知识点 平面的法向量,空间位置关系的向量证明,空间角的向量求法
【正确答案】
【试题解析】
19-1【基础】 如图在三棱锥P-ABC中,平面PAB⊥平面PBC,PB⊥BC,PD=DB=BC=AB=AD=2.
(1)证明:PA⊥平面ABC;
(2)求二面角B-AD-C的余弦值.
【正确答案】 (1)证明见解析;(2).
19-2【巩固】 如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥平面ABCD;
(2)若∠CBA=60°,求平面C1OB1与平面OB1D夹角的余弦值.
【正确答案】 (1)证明见解析;(2).
19-3【提升】 如图,在矩形中,,E为的中点,将沿折起到的位置,使得平面平面.
(1)证明:平面;
(2)求二面角的余弦值.
【正确答案】 (1)证明见解析;(2).
19-4【提升】 如图1,在边长为4的菱形ABCD中,∠BAD=60,DEAB于点E,将△ADE沿DE折起到△A1DE的位置,使A1DDC,如图2.
(1)求证:A1E平面BCDE;
(2)求二面角E—A1B—C的余弦值.
【正确答案】 (1)证明见解析;(2).
19-5【基础】 如图所示,在三棱柱中,,,四边形为菱形,,,D为的中点.
(1)证明:平面;
(2)若,求二面角的余弦值.
【正确答案】 (1)证明见解析;(2).
19-6【巩固】 如图在四棱锥中,底面为正方形,为等边三角形,E为中点,平面平面.
(1)求证:平面;
(2)求二面角的余弦值.
【正确答案】 (1)证明见解析;(2).
【原卷 20 题】 知识点 直线与圆的位置关系,抛物线标准方程的求法,抛物线的对称性
【正确答案】
【试题解析】
20-1【提升】 已知抛物线()的顶点为,直线与拋物线的交点(异于点)到点的距离为,
(1)求的标准方程;
(2)过点作斜率为()的直线与交于点(异于点),直线关于直线对称的直线与交于点(异于点),求证:直线过定点.
【正确答案】 (1);(2)证明见解析.
20-2【巩固】 如图,已知,直线,是平面上的动点,过点P作l的垂线,垂足为点Q,且.
(1)求动点P的轨迹C的方程;
(2)过点F的直线交轨迹C于A、B两点,交直线l于点M;
①已知,求的值;
②求的最小值.
【正确答案】 (1);(2)①;②.
20-3【提升】 已知椭圆:的焦距为,点在椭圆上,且的最小值是(为坐标原点).
(1)求椭圆的标准方程.
(2)已知动直线与圆:相切,且与椭圆交于,两点.是否存在实数,使得?若存在,求出的值;若不存在,请说明理由.
【正确答案】 (1);(2)存在
20-4【基础】 已知动圆过点,且与直线相切,设圆心的轨迹为曲线.
(1)求曲线的方程;
(2)设直线交曲线于,两点,以为直径的圆交轴于,两点,若,求的取值范围.
【正确答案】 (1);(2).
20-5【巩固】 已知抛物线C:()的焦点为F,原点O关于点F的对称点为Q,点关于点Q的对称点,也在抛物线C上
(1)求p的值;
(2)设直线l交抛物线C于不同两点A B,直线 与抛物线C的另一个交点分别为M N,,,且,求直线l的横截距的最大值.
【正确答案】 (1);(2)最大横截距为.
20-6【基础】 已知抛物线C:y2=4x,A,B,其中m>0,过B的直线l交抛物线C于M,N.
(1)当m=5,且直线l垂直于x轴时,求证:△AMN为直角三角形;
(2)若=+,当点P在直线l上时,求实数m,使得AM⊥AN.
【正确答案】 (1)证明见解析;(2)m=6.
【原卷 21 题】 知识点 利用导数研究函数的单调性,导数在函数中的其他应用
【正确答案】
【试题解析】
21-1【提升】 设函数().
(1)当时,试求下列问题:
①函数的单调区间;
②函数在的零点的个数;
(2)若函数在内有两个零点,求出的取值范围.
【正确答案】 (1)①的单调增区间为和,的单调递减区间为;②函数在有一个零点;(2).
21-2【巩固】 已知函数
(1)若在处有极值,求实数的值;
(2)求函数的单调区间;
(3)若函数有两个零点,求实数的范围.
【正确答案】 (1);(2)答案见解析;(3).
21-3【提升】 已知函数()
(1)当时,求的单调区间;
(2)若过点可作函数图像的三条不同切线,求实数的取值范围.
【正确答案】 (1)单调区间:,,;(2).
21-4【基础】 已知函数(为自然对数的底数)在处的切线与轴平行.
(1)求的单调区间;
(2)若在内有两个零点,求的取值范围.
【正确答案】 (1)在上单调递减,在上单调递增;(2).
21-5【巩固】 已知函数的定义域为.
(1)求的单调区间;
(2)讨论函数在上的零点个数
【正确答案】 (1)的单调递减区间为,单调递增区间为,(2)答案见解析
21-6【基础】 若函数,当时,函数有极值为.
(1)求函数的解析式;
(2)若有个解,求实数的取值范围.
【正确答案】 (1);(2).
【原卷 22 题】 知识点 极坐标与直角坐标的互化,圆的参数方程
【正确答案】
【试题解析】
22-1【巩固】 在平面直角坐标系中,曲线:,曲线:(为参数),以坐标原点为极点,轴正半轴为极轴建立极坐标系
(1)求曲线,的极坐标方程:
(2)射线:(,)分别交曲线,于,两点,求的最大值.
【正确答案】 (1):,:;(2)最大值为.
22-2【提升】 在直角坐标系中,以坐标原点为极点,轴的正半轴为极轴建立坐标系,曲线的极坐标方程为,曲线的参数方程为(为参数,).
(1)写出曲线的直角坐标方程;
(2)若曲线与有两个不同的交点,求实数的取值范围.
【正确答案】 (1)(2)
22-3【基础】 在直角坐标系xOy中,曲线C的参数方程为(m为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)求直线l的直角坐标方程;
(2)若直线l与曲线C交于点A,点P在曲线C上运动,求线段PA中点M轨迹的极坐标方程.
【正确答案】 (1);(2).
22-4【基础】 在平面直角坐标系中,圆C的参数方程为(α为参数),以坐标原点为极点,以x轴的正半轴为极轴建立极坐标系,且长度单位相同.
(1)求圆C的极坐标方程;
(2)若过原点的直线l被圆C截得的弦长为2,求直线l的倾斜角.
【正确答案】 (1);(2)直线l的倾斜角为或.
22-5【提升】 以直角坐标系的原点为极点,轴非负半轴为极轴建立极坐标系.在极坐标系中,曲线,点.在直角坐标系中,,,直线的参数方程为(为参数)
(1)将曲线的极坐标方程化为直角坐标方程,并判与4的大小关系;
(2)直线与曲线交于、两点,为曲线的右顶点,求的面积.
【正确答案】 (1),;(2).
22-6【巩固】 已知曲线,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为.
(1)写出曲线C的参数方程,直线l的直角坐标方程;
(2)设P是曲线C上任一点,求P到直线l的距离的最大值.
【正确答案】 (1)(为参数),;(2).
【原卷 23 题】 知识点 含绝对值不等式的解法,函数的图象
【正确答案】
【试题解析】
23-1【基础】 已知函数.
(1)解不等式;
(2)若正实数,满足,且函数的最小值为,求证:.
【正确答案】 (1);(2)证明见解析.
23-2【提升】 设实数x,y,z满足.
(1)证明:;
(2)若对任意的实数x,y,z,a恒成立,求实数m的取值范围.
【正确答案】 (1)证明见解析;(2)或.
23-3【提升】 已知函数.
(1)求不等式的解集;
(2)不等式的最小值为,若,为正数,且,证明:.
【正确答案】 (1);(2)证明见解析.
23-4【基础】 已知函数.
(1)解不等式;
(2)记函数的最小值为,且,其中均为正实数,求证:
【正确答案】 (1);(2)证明见解析.
23-5【巩固】 已知.
(1)求不等式的解集;
(2)若,求证:.
【正确答案】 (1);(2)证明见解析.
23-6【巩固】 设函数的最小值为.
(1)求的值;
(2)若,且,,用表示,,中的最大值,证明:
【正确答案】 (1)1;(2)证明见解析.
2021年高考理科数学甲卷 高三变式题库
/92 73是第21个素数,将其反过来37是第12个素数,同时7x3=21。
答案解析
2021年高考理科数学甲卷 高三变式题库
2021年高考理科数学甲卷 高三变式题库
/92 打好数学基础有两个必经过程:先学习、接受“由薄到厚”;再消化、提炼“由厚到薄”。——华罗庚
学习数学要多做习题,边做边思索。先知其然,然后知其所以然。——苏步青 /92
共性错题精讲
1-1【基础】 【正确答案】 B
【试题解析】 分析:
求出函数y=的定义域,得到集合N,再利用集合的交集的定义求解.
详解:
集合N={x|y=}={x|(x+2)(x﹣4)≥0}={x|x≤﹣2或x≥4},
∴M∩N={x|﹣4<x≤-2}.
故选:B.
1-2【巩固】 【正确答案】 A
【试题解析】 分析:
解出集合,利用并集的定义可求得集合.
详解:
,因此,.
故选:A.
1-3【巩固】 【正确答案】 C
【试题解析】 分析:
先求出集合P,Q,再利用集合的交集运算求解.
详解:
集合P={x∈N|x≤3}={0,1,2,3},Q={x|x2≤x+2}={x|﹣1≤x≤2},
∴P∩Q={0,1,2}.
故选:C.
1-4【基础】 【正确答案】 A
【试题解析】 分析:
化简得,根据集合并集运算即可.
详解:
解:化简得,
所以
故选:A.
1-5【提升】 【正确答案】 A
【试题解析】 分析:
先利用一元二次不等式的解法化简集合A,再利用交集运算求解.
详解:
∵,,
∴.
故选:A.
1-6【提升】 【正确答案】 A
【试题解析】 分析:
根据函数的定义域分别求出集合A、B,再根据交集的运算即可得出答案.
详解:
解:,
,
所以.
故选:A.
2-1【基础】 【正确答案】 C
【试题解析】 分析:
根据给定的柱状图分别求得健身前后各个区间上的人数,进行比较,即可求解.
详解:
根据给定的健身前后的体重柱状图,可得健身前体重在区间有人,健身后有,所以体重在区间内的人数增加了4个,所以A正确;
由健身前体重在的人数为人,健身后有,所以健身前后体重在的人数不变,所以B正确;
由健身前后体重再和的人数有明显变化,所以健身对体重有明显效果,所以C不正确;
由健身前体重在的人数为人,健身后为0人,所以原来体重在区间内的肥胖者体重都有减少,所以D正确.
故选:C.
点睛:
本题主要考查了统计图表的应用,其中解答中图表中的数据,分别计算求得健身前后各个区间的人数,进行比较是解答的关键,着重考查图表提取信息的能力,以及数据处理能力.
2-2【巩固】 【正确答案】 C
【试题解析】 分析:
根据频率分布直方图逐一计算分析.
详解:
A:用电量最多的一组有:人,故正确;
B:不低于度的有:人,故正确;
C:人均用电量:,故错误;
D:用电量在的有:人,所以,故正确;
故选C.
点睛:
本题考查利用频率分布直方图求解相关量,难度较易.频率分布直方图中平均数的求法:每一段的组中值后结果相加.
2-3【提升】 【正确答案】 B
【试题解析】 详解:
若①正确,则对应的频率为,
则对应的频率为,则②错误;
电子元件的平均寿命为,
则③正确;
寿命超过的频率为,则④正确,故不符合题意;
若②正确,则对应的频率为,则①错误;
电子元件的平均寿命为,
则③错误;
寿命超过的频率为,则④错误,故符合题意.
故选:B.
2-4【巩固】 【正确答案】 D
【试题解析】 分析:
利用频率分布直方图的性质直接求解.
详解:
解:对于,90分以上为优秀,由频率分布直方图得优秀的频率为,
从全体考生中随机抽取1000人,则其中得优秀考试生约有:人,故正确;
对于,由频率分布直方图得,的频率为,
,的频率为:,
若要全省的合格考通过率达到,则合格分数线约为44分,故正确;
对于,若同一组中数据用该组区间中间值作代表值,可得考试物理成绩的平均分约为:
分,故正确;
对于,,的频率为:,
,的频率为,
该省考生物理成绩的中位数为:分,故错误.
故选:.
点睛:
本题考查频数、合格分数线、平均数、中位数的求法,考查频率分布直方图的性质等基础知识,考查运算求解能力,属于基础题.
2-5【提升】 【正确答案】 C
【试题解析】 分析:
根据众数、中位数、平均值的概念等求值即可判断.
详解:
对于A,样本的众数为,A对;
对于B,设样本的中位数为,,解得,B对;
对于C,由直方图估计样本平均值为
,C错误;
对于D,2000名男生中体重大于的人数大约为,D对.
故选:C.
2-6【基础】 【正确答案】 C
【试题解析】 分析:
由频率分布直方图中的数据,以及频率、中位数、平均数的计算公式,逐项判定,即可求解.
详解:
根据此频率分布直方图,成绩在内的人数为人,所以A正确;
这名学生中成绩在内的频率为,所以B正确;
根据此频率分布直方图,可得这名学生成绩的中位数,所以C错误;
根据频率分布直方图的平均数的计算公式,可得:
,所以D正确.
故选:C.
3-1【提升】 【正确答案】 C
【试题解析】 分析:
先根据将化简,再根据复数的模的计算公式即可求出.
详解:
因为,
所以 .
故选:C.
点睛:
本题主要考查复数的模的计算公式的应用,属于容易题.
3-2【基础】 【正确答案】 A
【试题解析】 分析:
把已知等式变形,再利用复数代数形式的乘除运算化简得答案.
详解:
故选:A
3-3【提升】 【正确答案】 A
【试题解析】 分析:
由复数除法法则计算.
详解:
由已知
.
故选:A.
3-4【基础】 【正确答案】 B
【试题解析】 分析:
利用复数除法计算公式,即可得到结果.
详解:
.
故选:B
3-5【巩固】 【正确答案】 D
【试题解析】 分析:
由题意利用复数的运算法则整理计算即可求得最终结果.
详解:
由题意可得:.
故选:D.
3-6【巩固】 【正确答案】 A
【试题解析】 分析:
根据复数的除尘法则计算.
详解:
由已知.
故选:A.
4-1【基础】 【正确答案】 B
【试题解析】 分析:
根据题意构建指数函数模型,利用对数的运算进行计算即可得解.
详解:
设年后研发资金开始超过140万,
有,
所以,
由,所以,
所以第年研发资金开始超过140万元,
即2026年研发资金开始超过140万元.
故选:B
4-2【巩固】 【正确答案】 C
【试题解析】 分析:
利用对数的运算和对数函数的单调性求解.
详解:
当时,
,
当时,,
当时,,
当时,,
所以这4人中达到班级要求的有3人,
故选:C
4-3【基础】 【正确答案】 D
【试题解析】 分析:
根据已知条件列出式子求解即可.
详解:
解:由题意知:,
,
即,
即,
,
,
故正整数n的最小值为16.
故选:D.
4-4【提升】 【正确答案】 A
【试题解析】 分析:
根据题目所给数据求得,由此根据接收方收到明文“”,求得发送方发送的明文.
详解:
由其加密原理可知当时,,从而;
.
由解密原理可知当时,;
若接受方接到明文为“4”则有,,从而有,解得,
即发送方明文为.
故选:A
4-5【巩固】 【正确答案】 C
【试题解析】 分析:
根据小区内公共场所的声音的强度水平必须保持在50分贝以下,建立不等式,然后解对数不等式即可得到答案.
详解:
解:由题意可得,,即,
所以,解得,
所以声音强度的取值范围是,.
故选:C.
4-6【提升】 【正确答案】 A
【试题解析】 分析:
利用题设条件,计算出原信道容量的表达式,再列出在B不变时用所求平均噪声功率表示的信道容量的表达式,最后列式求解即得.
详解:
由题意可得,,则在信道容量未增大时,信道容量为,信道容量增大到原来的2倍时,,则,即,解得,
故选:A
5-1【提升】 【正确答案】 C
【试题解析】 分析:
由双曲线的定义可得,,结合已知条件可得,然后在直角三角形中利用勾股定理可求得答案
详解:
解:由双曲线的定义可得,,
因为,所以,
所以,即,
因为,
所以,所以,
由,得,
所以,得,
故选:C
5-2【提升】 【正确答案】 B
【试题解析】 分析:
设,则,然后由已知条件和双曲线的定义或求得,,再分别在和中,利用余弦定理列方程可求得,从而可求得离心率
详解:
解:设,则,
所以,
所以
因为,所以,
因为,所以
设,则,
在和中,由余弦定理得,
,
,
即,,
解得,
所以,
故选:B
5-3【巩固】 【正确答案】 D
【试题解析】 分析:
由题知,,计算得,由双曲线定义列出,计算可得离心率.
详解:
由题知,,又,且,则,
由双曲线定义得,,得
故选:D
5-4【巩固】 【正确答案】 A
【试题解析】 分析:
由圆的性质以及双曲线的定义得出,,再结合余弦定理以及离心率公式列出方程,求解即可.
详解:
取右焦点,连接
,
,即,
解得
故选:A
点睛:
关键点睛:解决本题的关键在于由余弦定理建立的齐次方程,从而得出离心率.
5-5【基础】 【正确答案】 D
【试题解析】 分析:
设的坐标为,函数的导数,根据条件可得,可解得,即,再根据双曲线的定义可求出其,从而得到离心率.
详解:
设的坐标为,由左焦点,所以
函数的导数,
则在处的切线斜率,
即,得,则,
设右焦点为,则,即,
,∴双曲线的离心率.
故选:D
5-6【基础】 【正确答案】 D
【试题解析】 分析:
由条件结合双曲线的定义可得,即,从而可得双曲线的离心率.
详解:
由双曲线的定义可得,∵,
∴,即,
则的离心率为.
故选:D.
6-1【巩固】 【正确答案】 A
【试题解析】 详解:
因为一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是
(0,0,2),(2,2,0),(0,2,0),(2,2,2).
画出几何体的直观图,如图
所以,以zOx平面为投影面,则得到正视图为AOC,
故选A.
6-2【基础】 【正确答案】 C
【试题解析】 分析:
本题首先可以通过三视图的几何性质得知三视图之间的联系,然后通过三视图的主视图与左视图来确定锥体的顶点所在的位置,最后对四个选项依次分析,即可得出结果.
详解:
本题中给出了主视图与左视图,故可以根据主视图与俯视图长对正,左视图与俯视图宽相等来找出正确选项,由主视图与左视图可知,锥体的顶点在左前方,
中的视图满足作图法则;中的视图满足作图法则;中的视图不满足锥体的顶点在左前方;中的视图满足作图法则,故选.
点睛:
本题考查了三视图的相关性质,主要考查了三视图中的主视图、左视图与俯视图的联系,考查空间想象能力,体现了基础性,是简单题.
6-3【提升】 【正确答案】 A
【试题解析】 详解:
试题分析:解题时在图的右边放扇墙(心中有墙),图所示方向的侧视图,由于平面仍在平面上,故侧视图中仍然看到左侧的一条垂直下边线段的线段,可得答案A,故选A.
考点:1、几何体的三视图;2、空间想象能力.
6-4【提升】 【正确答案】 B
【试题解析】 分析:
利用三视图的作图法则,对选项判断,①的三视图相同,圆锥,四棱锥的两个三视图相同,棱台都不相同,推出选项即可.
详解:
正方体的三视图分别为:正方形、正方形、正方形,圆锥的三视图分别为,三角形、三角形、圆和点.三棱台的三视图分别为:梯形和线段、梯形、大三角形内有小三角形,正四棱锥的三视图分别为:三角形、三角形、正方形和对角线,易知只有②④符合条件,故选B.
点睛:
本题主要考查几何体的三视图的识别能力,作图能力,学生的空间想象能力,三视图的投影规则是主视、俯视长对正;主视、左视高平齐,左视、俯视 宽相等,熟记常见几何体的三视图是解题的关键,属于基础题.
6-5【基础】 【正确答案】 D
【试题解析】 详解:
在空间直角坐标系中,根据所给的条件标出已知的四个点,结合三视图的画图规则,可得三棱锥的正视图和俯视图分别为④②.选D.
6-6【巩固】 【正确答案】 D
【试题解析】 详解:
由题意知三棱锥的侧视图即为三棱锥在侧面上的正投影,点点的投影为,点的投影为,点的投影为,故侧视图为上宽下窄的梯形,且左下到右上的对角线为实线,左上到右下的对角线为虚线,故D选项满足.选D.
点睛:三视图的三种题型
(1)已知几何体画出三视图,解题时要注意画三视图的规则;
(2)已知三视图还原几何体,要综合三个视图得到几何体的形状;
(3)已知三视图研究几何体,如根据三视图求几何体的体积或表面积等.
7-1【提升】 【正确答案】 D
【试题解析】 分析:
根据已知求得的范围,然后根据的正负分类讨论确定的单调性.
详解:
因为,所以,,即,
若,,,是递增数列,排除AC,
若,则,,易知,,是摆动数列,排除B,
当时,是递增数列,是最小项.
当时,,,
所以,所以中是最小项.D正确.
故选:D.
点睛:
关键点点睛:本题考查数列的单调性,解题关键是通过与的关系进行判断,难点是摆动数列的最小项问题,需要利用进行证明.
7-2【巩固】 【正确答案】 D
【试题解析】 分析:
由题可得,利用条件可得出,进而可得.
详解:
∵,
∴,
∵,
>0,
∵a1=2,
∴,……
∴数列{bn}是递减数列.
故选:D.
7-3【巩固】 【正确答案】 D
【试题解析】 分析:
由已知式变形,再写一次(用换)可得,这样.然后根据利用等差中项法判断等差数列,利用定义判断数列的单调性.
详解:
由题意知,则,
从而,
则,
因此.
对于选项A,C,当时,
,
从而,
故数列不可能是等差数列,因此选项A错误,
若,则,
从而,
即,
因此数列是递减的,因此选项C错误;
对于选项B,D,当时,
,
从而,
故数列不可能是等差数列,因此选项B错误,
若,则,
从而,
即,
因此数列是递减的,选项D正确.
故选:D.
点睛:
关键点点睛:本题考查等差数列的判断,数列的单调性,解题关键是对已知递推关系变形得出是常数,根据利用等差数列和单调性的概念判断.
7-4【提升】 【正确答案】 D
【试题解析】 分析:
根据数列的单调性的定义,结合不等式的性质、对钩函数的单调性进行求解即可.
详解:
,,
所以当时,,
当时,数列是递增数列,
因此有或,而,所以,
因此必有或,而,
所以有或,因此选项A,C不正确;
因为,所以选项B不正确;
当时,数列是递增数列,故,
,而函数在时,单调递增,故数列是单调递增数列;
,而函数在时,单调递增,故数列为单调递增数列.
故选:D
点睛:
本题考查了数列的单调性判断,考查了对钩函数的单调性的应用,考查了数学运算能力.
7-5【基础】 【正确答案】 B
【试题解析】 分析:
利用特例法证明充分性不成立;当成立时,两边平方可得 ,则数列为递减数列成立,即必要性满足.
详解:
由题意可得:数列的项都是实数,
当数列为递减数列时,如:数列的通项为,
此时不成立,即充分性不满足;
当成立时,有,
两边平方可得:即有,
因此数列为递减数列成立,
所以“数列为递减数列”是“”的必要不充分条件
故选:B
点睛:
本题考查了递减数列概念以及判断充分条件,必要条件,属于一般题.
7-6【基础】 【正确答案】 B
【试题解析】 分析:
根据充分发条件的定义判断.
详解:
是递增数列,则必有,必要性满足,
若,,满足,但,数列不是递增数列,充分性不满足.
应是必要不充分条件,
故选:B.
点睛:
本题考查充分必要条件的判断,掌握充分必要条件的定义是解题关键.
8-1【基础】 【正确答案】 B
【试题解析】 分析:
在和中,利用正切值可求得,进而求得.
详解:
在中,(米),
在中,(米),
(米).
故选:.
点睛:
本题考查解三角形的实际应用中的高度问题的求解,属于基础题.
8-2【基础】 【正确答案】 C
【试题解析】 分析:
在中,由条件可得,再在中,由可得解.
详解:
如图所示,在中,由正弦定理可得 ,
由,,
所以,
在中,.
故选:C.
8-3【巩固】 【正确答案】 B
【试题解析】 分析:
设的高度为,在直角三角形中用表示出,由可求得得楼高.
详解:
设的高度为,
则由已知可得,,,
所以,解得,
所以楼高(米).
故选:B.
点睛:
本题考查解三角形的实际应用.属于基础题.
8-4【巩固】 【正确答案】 D
【试题解析】 分析:
由正弦得出,再结合正弦定理得到,进而能求.
详解:
由题意知:,所以
在中,,
在中,由正弦定理得 所以 ,
在中,
故选:D
8-5【提升】 【正确答案】 A
【试题解析】 分析:
利用平面相似的有关知识以及合分比性质即可解出.
详解:
如图所示:
由平面相似可知,,而 ,所以
,而 ,
即= .
故选:A.
点睛:
本题解题关键是通过相似建立比例式,围绕所求目标进行转化即可解出.
8-6【提升】 【正确答案】 A
【试题解析】 分析:
根据C点的仰角∠CAB=45°,山高BC=100 m,可求出AC,正弦定理求出AM,在三角形MAN中即可解出山高.
详解:
由题意∠CAB=45°,BC=100 m,,三角形ABC为直角三角形,可得,在中,∠MAC=75°,∠MCA=60°,则∠AMC=45°
由正弦定理有:
即
故
在直角三角形中,
可得
故选:
点睛:
解三角形应用题的一般步骤:
(1)阅读理解题意,弄清问题的实际背景,明确已知与未知,理清量与量之间的关系.
(2)根据题意画出示意图,将实际问题抽象成解三角形问题的模型.
(3)根据题意选择正弦定理或余弦定理求解.
(4)将三角形问题还原为实际问题,注意实际问题中的有关单位问题、近似计算的要求等.
9-1【巩固】 【正确答案】 A
【试题解析】 详解:
,,
,即,故
故选
9-2【提升】 【正确答案】 C
【试题解析】 分析:
由所给等式利用同角三角函数的关系可求得,再利用降幂公式及二倍角公式将整理为,代入相应值即可得解.
详解:
由可得
所以,即,即
故选:C
点睛:
关键点睛:本题考查同角三角函数的关系、降幂公式、二倍角公式,解答本题的关键是由条件有,从而可得,由可解,属于中档题.
9-3【基础】 【正确答案】 D
【试题解析】 分析:
首先由角知,再利用同角三角函数平方关系求,二倍角余弦公式以及诱导公式求即可.
详解:
,
,
又,
.
.
故选:D.
9-4【巩固】 【正确答案】 A
【试题解析】 分析:
由同角三角函数的基本关系可求得的值,再利用弦化切以及二倍角的正弦和余弦公式可求得所求代数式的值.
详解:
,是第三象限角,,
因此,,
故选:A.
点睛:
方法点睛:三角函数的化简求值的规律总结:
(1)给角求值:一般给出的角是非特殊角,需观察所给角与特殊角的关系,利用三角变换转化为特殊角的三角函数问题;
(2)给值求值:即给出某些角的三角函数值,求另外一些角的三角函数值,解题关键在于“变角”,使相关角相同或具有某种关系;
(3)给值求角:实质上可转化为“给值求值”,即通过求角的某个三角函数值来求角(注意角的取值范围).
9-5【提升】 【正确答案】 C
【试题解析】 分析:
将式子先利用二倍角公式和平方关系配方化简,然后增添分母(),进行齐次化处理,化为正切的表达式,代入即可得到结果.
详解:
将式子进行齐次化处理得:
.
故选:C.
点睛:
易错点睛:本题如果利用,求出的值,可能还需要分象限讨论其正负,通过齐次化处理,可以避开了这一讨论.
9-6【基础】 【正确答案】 A
【试题解析】 分析:
由同角三角函数的基本关系计算可得、,再根据两角差的正切公式计算可得.
详解:
解:因为,所以,又,
所以,则,
所以.
故选:
点睛:
本题考查三角恒等变换,考查运算求解能力,属于基础题.
10-1【基础】 【正确答案】 B
【试题解析】 分析:
甲和乙参加的概率为,甲和乙演讲顺序不相邻的概率为,由此能求出甲和乙参加,且演讲顺序不相邻的概率.
详解:
甲和乙参加的概率为,甲和乙演讲顺序不相邻的概率为,
所求概率为;或直接为.
故选:B.
10-2【提升】 【正确答案】 D
【试题解析】 详解:
从分别写有1,2,3,4,5的5张卡片中随机抽取1张,放回后再随机抽取1张,
基本事件总数n=5×5=25,
抽得的第一张卡片上的数大于第二张卡片上的数包含的基本事件有:
(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(5,4),
共有m=10个基本事件,
∴抽得的第一张卡片上的数大于第二张卡片上的数的概率p=
故答案为D.
10-3【基础】 【正确答案】 B
【试题解析】 分析:
本题首先用列举法写出所有基本事件,从中确定符合条件的基本事件数,应用古典概率的计算公式求解.
详解:
设其中做过测试的3只兔子为,剩余的2只为,则从这5只中任取3只的所有取法有,共10种.其中恰有2只做过测试的取法有共6种,
所以恰有2只做过测试的概率为,选B.
点睛:
本题主要考查古典概率的求解,题目较易,注重了基础知识、基本计算能力的考查.应用列举法写出所有基本事件过程中易于出现遗漏或重复,将兔子标注字母,利用“树图法”,可最大限度的避免出错.
10-4【提升】 【正确答案】 D
【试题解析】 分析:
利用分步计数原理求出不同的涂色方案有420种,其中,区域涂色不相同的情况有120种,由此根据古典概型概率公式能求出区域涂色不相同的概率.
详解:
提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,
根据题意,如图,设5个区域依次为,分4步进行分析:
,对于区域,有5种颜色可选;
,对于区域与区域相邻,有4种颜色可选;
,对于区域,与区域相邻,有3种颜色可选;
,对于区域,若与颜色相同,区域有3种颜色可选,
若与颜色不相同,区域有2种颜色可选,区域有2种颜色可选,
则区域有种选择,
则不同的涂色方案有种,
其中,区域涂色不相同的情况有:
,对于区域,有5种颜色可选;
,区域,有4种颜色可选;
对于区域,有3种颜色可选;
,若与颜色相同,区域有2种颜色可选;
若与颜色不相同,区域有2种颜色可选,区域有1种颜色可选;
所以区域有种选择;
不同的涂色方案有种,
区域涂色不相同的概率为 ,故选D.
点睛:
本题考查古典概型概率公式的应用,考查分步计数原理等基础知识,考查运算求解能力,是中档题.在求解有关古典概型概率的问题时,首先求出样本空间中基本事件的总数,其次求出概率事件中含有多少个基本事件,然后根据公式求得概率.
10-5【基础】 【正确答案】 A
【试题解析】 分析:
本题主要考查利用两个计数原理与排列组合计算古典概型问题,渗透了传统文化、数学计算等数学素养,“重卦”中每一爻有两种情况,基本事件计算是住店问题,该重卦恰有3个阳爻是相同元素的排列问题,利用直接法即可计算.
详解:
由题知,每一爻有2种情况,一重卦的6爻有情况,其中6爻中恰有3个阳爻情况有,所以该重卦恰有3个阳爻的概率为=,故选A.
点睛:
对利用排列组合计算古典概型问题,首先要分析元素是否可重复,其次要分析是排列问题还是组合问题.本题是重复元素的排列问题,所以基本事件的计算是“住店”问题,满足条件事件的计算是相同元素的排列问题即为组合问题.
10-6【基础】 【正确答案】 C
【试题解析】 分析:
分别安排各场馆的志愿者,利用组合计数和乘法计数原理求解.
详解:
首先从名同学中选名去甲场馆,方法数有;
然后从其余名同学中选名去乙场馆,方法数有;
最后剩下的名同学去丙场馆.
故不同的安排方法共有种.
故选:C
点睛:
本小题主要考查分步计数原理和组合数的计算,属于基础题.
11-1【巩固】 【正确答案】 C
【试题解析】 分析:
求出矩形的对角线长,进而可得球心到矩形所在平面的距离即棱锥的高,再由棱锥的体积公式即可得解.
详解:
∵矩形的顶点都在半径为5的球面上,且,,
∴矩形的对角线长为,
∴球心到矩形所在平面的距离为,
所以棱锥的体积.
故选:C.
点睛:
本题考查了球的几何特征的应用及几何体体积的求解,考查了运算求解能力与空间思维能力,属于基础题.
11-2【基础】 【正确答案】 D
【试题解析】 分析:
先由球的截面的性质可得球的半径,再由正方体外接球的直径即为体对角线的长即可得解.
详解:
由题意,的外接圆半径为,
设该球的半径为,可得,所以,
设该球内接正方体的棱长为,所以,所以.
故选:D.
11-3【提升】 【正确答案】 C
【试题解析】 分析:
设三角形ABC的外接圆的圆心为O',根据球的截面性质可知OO'⊥平面ABC,利用正弦定理求得AO',计算球的半径,进而求得体积.
详解:
设三角形ABC的外接圆的圆心为O',根据球的截面性质可知OO'⊥平面ABC,
如图所示,∵,∴AO'=,
∴OA=
∴球的体积为,
故选:C.
11-4【巩固】 【正确答案】 D
【试题解析】 分析:
求出外接圆半径,再利用球面的截面小圆的性质求出球半径即可作答.
详解:
因,,则,即,于是得外接圆半径,
又点、、在同一个球面上,且球心到平面的距离为1,则球半径,
所以球的表面积为.
故选:D
11-5【提升】 【正确答案】 C
【试题解析】 分析:
由题意画出图形,由是面积为的等边三角形,可得,再由球的体积为,求出球的半径,而,再利用勾股定理可求出结果
详解:
由题意可知图形如图:是面积为的等边三角形,
可得,
∴,
可得:,
球的体积,解得,
所以到平面的距离为:.
故选:C.
点睛:
此题考查球截面性质,考查空间想象能力和计算能力,属于基础题
11-6【基础】 【正确答案】 D
【试题解析】 分析:
由截面圆的面积求出截面圆半径,根据截面圆半径、球的半径和球心到平面的距离之间的关系即可求解球的半径,进而求表面积.
详解:
如图所示:
设截面圆的半径为,球的半径为,球心到平面的距离为
因为截面圆的面积为,得,又
由图可得
则球的表面积为
故选:D.
12-1【巩固】 【正确答案】 A
【试题解析】 分析:
先求出函数的解析式,将代入计算即可.
详解:
因为函数在定义域上单调,且,
所以为常数,不妨设,则
由得,解得:,
所以,
所以.
故选:A
12-2【基础】 【正确答案】 C
【试题解析】 分析:
根据题意求得函数的周期,结合函数性质,得到,在代入解析式求值,即可求解.
详解:
因为为上的偶函数,所以,
又因为对于,都有,
所以函数的周期,且当时,,
所以
故选:C.
12-3【巩固】 【正确答案】 A
【试题解析】 分析:
由奇函数和,可得周期,转化
,即得解
详解:
由题意,函数是上的奇函数,满足
因此函数的周期
故选:A
12-4【基础】 【正确答案】 B
【试题解析】 分析:
利用函数的奇偶性和周期性求解.
详解:
因为函数是定义域为R的奇函数,周期为2,且当时,,
所以 ,
故选:B
12-5【提升】 【正确答案】 B
【试题解析】 详解:
分析:由题意,得到函数是周期为的函数,进而可求得的值.
详解:由题意可得:,即函数是周期为的函数,
则,
故选B.
点睛:本题考查了函数的基本性质的应用,对于函数的三个性质:单调性、奇偶性和周期性,常将它们综合在一起考查,其中单调性与奇偶性结合、周期性与抽象函数相结合,并结合奇偶性求函数值,多以选择题、填空题的形式呈现,且主要有以下几种命题角度:
(1)函数的单调性与奇偶性相结合,注意函数的单调性及奇偶性的定义,以及奇、偶函数图象的对称性.
(2)周期性与奇偶性相结合,此类问题多考查求值问题,常利用奇偶性及周期性进行交换,将所求函数值的自变量转化到已知解析式的函数定义域内求解.
(3)周期性、奇偶性与单调性相结合,解决此类问题通常先利用周期性转化自变量所在的区间,然后利用奇偶性和单调性求解.
12-6【提升】 【正确答案】 A
【试题解析】 详解:
分析:根据奇函数与偶函数的定义,可求得函数的解析式;根据解析式确定’的值.
详解:令 ,
则,因为为偶函数
所以(1)
,因为 为奇函数
所以(2)
(1)-(2)得
(3),令 代入得
(4)
由(3)、(4)联立得
代入得
所以
所以
所以选A
点睛:本题考查了抽象函数解析式的求解,主要是利用方程组思想确定解析式.方法相对比较固定,需要掌握特定的技巧,属于中档题.
13-1【提升】 【正确答案】
【试题解析】 分析:
先将曲线变形,再通过求导求曲线在处的切线方程,再求面积.
详解:
由可得时,.,,则切线方程为即.
切线与两坐标轴的交点分别为,所以三角形的面积为.
点睛:
求过曲线上一点的切线方程一般有两种思路:1、设切线的斜率,联立曲线方程和直线方程通过判别式加以判断;2、通过求导求曲线在这个点处的斜率,进而求出切线方程.此题曲线是双曲线,若用判别式法求解,则求出的结果要注意检验.用求导求解要注意所得解析式中.
13-2【基础】 【正确答案】
【试题解析】 分析:
到处导函数,再求出切线方程,即可得到横纵截距之和.
详解:
由题:,
,,
所以在点处切线方程,即
当,
当,
所以该切线的横纵截距之和为.
故答案为:
点睛:
此题考查求曲线在某点处的切线方程,再求直线截距,关键在于根据题意准确计算.
13-3【巩固】 【正确答案】
【试题解析】 分析:
根据导数几何意义得切线斜率,再根据点斜式得结果.
详解:
因为,所以,因此在x=0处的切线斜率为,
因为x=0时,所以切线方程是
点睛:
本题考查导数几何意义,考查基本求解能力.属基础题.
13-4【提升】 【正确答案】
【试题解析】 详解:
设,则,
,
据此可得:,
且:,
据此可得:曲线在处的切线方程是,
整理为一般式即:.
点睛:导数运算及切线的理解应注意的问题
一是利用公式求导时要特别注意除法公式中分子的符号,防止与乘法公式混淆.
二是直线与曲线公共点的个数不是切线的本质,直线与曲线只有一个公共点,直线不一定是曲线的切线,同样,直线是曲线的切线,则直线与曲线可能有两个或两个以上的公共点.
三是复合函数求导的关键是分清函数的结构形式.由外向内逐层求导,其导数为两层导数之积.
13-5【基础】 【正确答案】
【试题解析】 分析:
求导得到,计算,,得到切线方程.
详解:
,则,故,
故切线方程为:,即
故答案为:
点睛:
本题考查了切线方程,意在考查学生的计算能力.
13-6【巩固】 【正确答案】 2x﹣y﹣1=0
【试题解析】 分析:
求出f(x)的导数,可得切线的斜率和切点,即可得到所求切线的方程.
详解:
函数f(x)=lnx+x的导数为,
可得函数f(x)的图象在x=1处的切线斜率为k=2,
切点为(1,1),
可得切线的方程为y﹣1=2(x﹣1);即2x﹣y﹣1=0.
故答案为2x﹣y﹣1=0.
点睛:
本题考查利用导数求切线的方程,是基本题.
14-1【巩固】 【正确答案】
【试题解析】 分析:
首先根据向量线性运算的坐标表示求出,再计算数量积即可;
详解:
解:因为,,
所以,
所以
故答案为:
14-2【提升】 【正确答案】
【试题解析】 分析:
先求的坐标,再利用列方程即可求解.
详解:
因为,,所以,
因为,
所以,解得,
故答案为:.
14-3【提升】 【正确答案】
【试题解析】 分析:
根据向量垂直和平行的坐标运算法则计算得,,得出,再根据向量的模的坐标公式即可求得结果.
详解:
因为向量,,,
且,,
∴
解得,;
∴,;
∴,
∴.
故答案为:
14-4【基础】 【正确答案】
【试题解析】 分析:
根据向量垂直的坐标表示以及平面向量的数量积列方程可解得结果.
详解:
因为向量,,且向量与垂直,
所以,
所以,
所以,解得.
故答案为:
14-5【巩固】 【正确答案】 (或135°)
【试题解析】 分析:
根据向量,求得向量的坐标,再利用向量的夹角公式求解.
详解:
因为向量,
所以,
所以,
因为,
所以,
故答案为:(或135°)
14-6【基础】 【正确答案】 或2
【试题解析】 分析:
转化为,即得解
详解:
已知,,若,
则,,,,
,,
,
,或,
故答案为:或2.
点睛:
本题考查了向量垂直的坐标表示,考查了学生概念理解,数学运算能力,属于基础题
15-1【基础】 【正确答案】
【试题解析】 分析:
由椭圆得b,c,由此能求面积
详解:
由题,则四边形的面积为
故答案为
点睛:
本题考查椭圆的面积问题,是基础题
15-2【提升】 【正确答案】 9
【试题解析】 分析:
设出p点的坐标(x1,y1),根据PF1⊥PF2,求出y1,再根据 求面积.
详解:
解:椭圆C:1的左、右焦点分别为F1(﹣4,0)、F2(4,0),
设P(x1,y1),由已知PF1⊥PF2,所以 ,
即 (﹣4﹣x1,﹣y1) (4﹣x1,﹣y1)=0,
∴x12+y12=16,
又因为 1,
解得 ,所以,△PF1F2的面积.
故答案为9.
点睛:
本题考查了椭圆的标准方程、椭圆的简单性质以及根据一些性质求面积,用到数形结合思想,这是高中数学的一种重要思想.
15-3【巩固】 【正确答案】 64.
【试题解析】 分析:
根据题目三角形且满足,为椭圆的两个焦点,点在椭圆上,则可利用椭圆的性质,根据完全平方公式和勾股定理可得的值,即可求得三角形的面积.
详解:
由椭圆可得.
为椭圆的两个焦点,点在椭圆上,
可得①,
∵,
∴②,
①式平方可得,
整理得,
∴,
故答案为:64.
点睛:
本题考查椭圆的简单几何性质,利用完全平方公式及直角三角形三边关系,解出直角边之积进而得到三角形面积,属于简单题.
15-4【基础】 【正确答案】 2
【试题解析】 分析:
将椭圆方程化为标准方程,求得,根据焦点坐标与顶点坐标求得三角形面积.
详解:
椭圆方程可化为.
,从而.
因此,两焦点为,短轴的个端点为.
∴构成的三角形的面积为.
故答案为:2.
点睛:
本题主要考查椭圆的简单几何性质,属基础题.
15-5【巩固】 【正确答案】 9
【试题解析】 分析:
根据椭圆的方程求得c,得到|F1F2|,设出|PF1|=t1,|PF2|=t2,利用勾股定理以及椭圆的定义,可求得t1t2的值,即可求出三角形面积.
详解:
∵a=5,b=3;∴c=4,
设|PF1|=t1,|PF2|=t2,
则t1+t2=10①t12+t22=82②,
由①2﹣②得t1t2=18,
∴.
故答案为9.
点睛:
本题主要考查了椭圆的标准方程、椭圆的简单性质.解答的关键是通过勾股定理解三角形,考查计算能力.
15-6【提升】 【正确答案】 3
【试题解析】 分析:
令|F1P|=m、|PF2|=n,由椭圆的定义得 m+n,在Rt△F1PF2中,由勾股定理得m2+n2,从而可得m n的值,即得△F1PF2的面积,从而得到答案.
详解:
令|F1P|=m、|PF2|=n,由椭圆的定义可得 m+n=2a①,
Rt△F1PF2 中,由勾股定理可得(2c)2=m2+n2②,由①②可得mn=2b2,
∴△F1PF2的面积是==9,即b=3,
故答案为3.
点睛:
本题考查三角形面积的计算,考查椭圆的定义,考查勾股定理,考查学生的计算能力,属于基础题.
16-1【巩固】 【正确答案】
【试题解析】 分析:
根据图象可得,由题意得出,即可求出,再代入即可求出,进而得出所求.
详解:
由函数图象可得,
相邻的两条对称轴之间的距离为,,则,,
,
又,即,,或,
根据“五点法”画图可判断,,
.
故答案为:.
16-2【基础】 【正确答案】
【试题解析】 分析:
根据最大值得,再由图像得周期,从而得,根据时,取得最大值,利用整体法代入列式求解,再结合的取值范围可得.
详解:
根据图像的最大值可知,,由,可得,所以,再由得,,所以,因为,所以,故函数的解析式为.
故答案为:.
16-3【提升】 【正确答案】
【试题解析】 分析:
根据函数图象有,可求得,又函数图象过点,点,代入可求得,,求得,然后利用函数的周期性求解.
详解:
由图可知:,,
所以函数,
又函数图象过点,点,,
,
所以,
,
故答案为:
点睛:
方法点睛:求函数解析式的步骤:
(1)求A,B,确定函数的最大值M和最小值m,则,.
(2)求,确定函数的周期,则
(3)求,常用方法如下:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入.
16-4【巩固】 【正确答案】
【试题解析】 分析:
由题意利用函数的图象变换规律,得到的解析式,再根据正弦函数的单调增区间,求得的取值范围.
详解:
解:将函数的图象向左平移个单位,
得到函数 的图象.
若在区间上为增函数,则,且,
求得,则的取值范围为,,
故答案为:,.
16-5【提升】 【正确答案】
【试题解析】 分析:
原问题转化为在区间上至少有2个,至多有3个t,使得,求得取值范围,作出可知,满足条件可最短区间长度为,最长区间长度为,由此建立关于的不等式,解出即可.
详解:
令,则,令,则,
则原问题转化为在区间上至少有2个,至多有3个t,使得,求得取值范围,
作出与的图象,如图所示,
由图可知,满足条件可最短区间长度为,最长区间长度为,
∴,解得.
故答案为:.
16-6【基础】 【正确答案】
【试题解析】 分析:
由正弦函数的图象求得,令利用导数求其最值,由题设不等式恒成立知,结合三角形内角的性质求的取值范围.
详解:
由图知:,,即,可知.
由,得,,
∴,,又,即,
∴.
设,则,
当时,,单调递减,
当时,,单调递增,
∴,即,得.
由,得.
结合正弦函数的图象可知,当时成立,
∴的范围是.
故答案为:
17-1【基础】 【正确答案】 有99%的把握认为该血清能起到预防感冒的作用.
【试题解析】 分析:
利用公式计算得出数据,比较数据大小得解
详解:
解:设H0:感冒与是否使用该血清没有关系.
因当H0成立时,χ2≥6.635的概率约为0.01,故有99%的把握认为该血清能起到预防感冒的作用.
P(χ≥x0) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828
17-2【巩固】 【正确答案】 在犯错的概率不超过0.1的前提下可以认为性别与出生时间有关联.
【试题解析】 分析:
根据题目所给的数据,计算,对照参数即可下结论.
详解:
由题意得的观测值为:
,
∴在犯错的概率不超过0.1的前提下可以认为性别与出生时间有关联.
17-3【巩固】 【正确答案】 (1)列联表见解析;有的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”;(2)答案见解析.
【试题解析】 分析:
(1)根据已知数据补全列联表,利用公式计算得到,由此可得结论;
(2)根据数据可知个体经营户配合度需提高,由此可确定统计建议.
详解:
(1)根据已知数据,完成列联表如下:
顺利 不顺利 合计
企事业单位 40 10 50
个体经营户 100 50 150
合计 140 60 200
,
有的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”.
(2)建议:加大宣传力度,消除误解因素,尤其要做好个体经营户的思想工作.(意思相近即可)
17-4【提升】 【正确答案】 没有充分证据认为“成绩与班级有关系”.
【试题解析】 分析:
计算出卡方值,即可判断.
详解:
计算得的观测值为,
因为0.653<3.841,所以没有充分证据认为“成绩与班级有关系”.
17-5【基础】 【正确答案】 (1)表格见解析;(2)没有的把握认为参加体育锻炼与否跟性别有关.
【试题解析】 分析:
(1)根据调查结果完成列联表即可;
(2)根据列联表计算,与附表对照,即可判断.
详解:
解:(1)填写的列联表如下
男性居民 女性居民 合计
不参加体育锻炼
参加体育锻炼
合计
(2)计算
因为.
所以没有的把握认为参加体育锻炼与否跟性别有关.
点睛:
本题考查了利用独立性检验解决实际问题,属于基础题.
17-6【提升】 【正确答案】 (1)答案见解析;(2),没有90%的把握认为“成绩与班级有关”.
【试题解析】 分析:
(1)根据条形图中数据完成表格即可;
(2)根据公式计算出的值,然后可得答案.
详解:
(1)根据条形图中的数据可得如下表格,
甲班 乙班 总计
优秀 15 20 35
非优秀 40 30 70
总计 55 50 105
(2)
因为,所以没有90%的把握认为“成绩与班级有关”.
点睛:
本题考查的是独立性检验,考查了学生的计算能力,属于基础题.
18-1【基础】 【正确答案】 选①和②得结果相同,(1);(2)
【试题解析】 分析:
(1)选①②直接根据数列的递推关系式求出公比,从而可求得数列的通项公式;
(2)直接利用(1)的结论,进一步利用分组求和法求出数列的前项和.
详解:
解:(1)选条件①
设数列的公比为,由得,
∴即或;又数列是正项数列,故.
从而数列的通项公式为:.
选条件②
设数列的公比为,由,,成等差数列,∴,
所以,解得,
从而数列的通项公式为:.
(2),
.
18-2【巩固】 【正确答案】 选①②③结果均相同,(Ⅰ);(Ⅱ)见解析;(Ⅲ)
【试题解析】 分析:
分别选①②③,(Ⅰ)由数列的递推式或等差数列的定义和性质,可得公差,通项公式;
(Ⅱ)由等比数列的定义,可得证明;
(Ⅲ)求得,由数列的分组求和,结合等差数列和等比数列的求和公式,可得所求和.
详解:
解:选①,(Ⅰ)因为,时,,
则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
.
选②,(Ⅰ)由,,则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
.
选③,(Ⅰ)由,且,
可得数列为等差数列,设公差为,
则,
则,;
(Ⅱ)证明:,
可得,
所以数列是首项为和公比均为4的等比数列;
(Ⅲ),
所以
.
18-3【提升】 【正确答案】 (1);(2)答案不唯一,具体见解析.
【试题解析】 分析:
(1)设等差数列的首项为,公差为d,解方程组即得数列的通项公式及;(2)选①:利用错位相减法求和得解;选②:利用裂项相消法求和得解;选③:对分两种情况讨论求和得解.
详解:
(1)设等差数列的首项为,公差为d,
,所以,
.
(2)选①:
①
②
由①-②得,
选②:,
所以,
所以
选③:
当n为偶数时,
当n为奇数时,
所以.
18-4【巩固】 【正确答案】 (1),;(2).
【试题解析】 分析:
(1)根据题中条件求解数列的基本参数进而求解出数列的通项公式;
(2)先求解数列的前n项和,结合不等式恒成立问题求解出参数的范围.
详解:
(1)时,
时,
n=1时,,∴.
由得,
∵,∴,所以,
∴,;
(2),
,
,;令,
,∴,
∴,∴实数的取值范围为.
18-5【提升】 【正确答案】 (1)若选①,,若选②,,若选③,;(2)若选①,
,若选②, ,若选③, .
【试题解析】 分析:
(1)根据,,成等比数列,用等差数列的基本量进行运算,可得首项和公差的关系,结合条件即可得到答案;
(2)由(1)解出的通项公式,进而根据分组求和即可得到答案.
详解:
(1)设数列的公差为.因为,,成等比数列,则,
故,化简得.因为,所以,所以.
若选①,则,即,则;
若选②,则,即,则;
若选③,则,即,则;
(2)因为数列是各项均为正数的等比数列,且,,
设数列的公比为,则.
若选①,则,故,,
所以,由,得.又,则,所以,
所以.
若选②,则,故,,
所以,由,得.又,则,所以,
所以.
若选③,则,故,,
所以,由,得.又,则,所以,
则.
18-6【基础】 【正确答案】 (1);(2)答案见解析.
【试题解析】 分析:
(1)根据求解即可;
(2)选①利用错位相减法求和即可;选②利用裂项相消法求和即可;选③对分奇偶讨论,然后利用并项求和法求和即可.
详解:
(1)∵在数列中,.
当时,,
当时,,
又也满足,
∴
(2)选择条件①,
∴①
②
①-②得
故.
选择条件②由(1)知:,
∴
∴
选择条件③
,
∴当为偶数时,
当为奇数时,
综上所述:.
19-1【基础】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)由侧面PAB⊥平面PBC,可得BC⊥侧面PAB,所以PA⊥BC,再由PD=DB=DA,所以PA⊥AB,利用线面垂直的判定定理即得证;
(2)建立空间直角坐标系,求出两个平面的法向量,利用二面角的向量计算公式,即得解.
详解:
(1)侧面PAB⊥平面PBC,PB⊥BC,所以BC⊥侧面PAB
又PA侧面PAB,所以PA⊥BC
又PD=DB=DA,可得,
又内角和为
所以PA⊥AB
又ABBC=B,所以PA⊥平面ABC
(2)以A为原点,过点A作BC的平行线为x轴,AB,AP所在直线分别y z轴,建立空间直角坐标系,如图所示.
在直角三角形PAB中,,由已知得:.
,
设平面ACD的法向量为,
则,即,取,则,
故
设平面ABD的法向量为,
又二面角A-PD-C为锐角,故二面角A-PD-C的余弦值为
故答案为:.
点睛:
本题考查了面面垂直的性质,线面垂直的判定,以及向量法求二面角,考查了学生综合分析,逻辑推理,数学运算的能力,属于中档题
19-2【巩固】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)由已知中,四棱柱的所有棱长都相等,,,四边形和四边形均为矩形.可得且,,进而,,再由线面垂直的判定定理得到底面;
(2)设四棱柱的所有棱长均为,设为2,若,,,以为坐标原点,分别以,,为,,轴正方向建立空间直角坐标系,求出平面和平面的法向量,代入向量夹角公式,求出二面角的余弦值.
详解:
证明:(1)四棱柱的所有棱长都相等,
四边形为菱形,
又,
故为的中点,
同理也是的中点,
又四边形和四边形均为矩形,
且,,
,,
又,,平面,
底面;
解:(2)设四棱柱的所有棱长均相等,所以四边形是菱形,
,
又底面,
,,两两垂直,
如图,以为坐标原点,,,所在直线分别为轴,轴,轴建立直角坐标系.
设,
,
,,
则,,,
易知,是平面的一个法向量,
设,,是平面的一个法向量,则,即
取,则,,所以,,
设二面角的大小为,易知是锐角,于是:
,
故二面角的余弦值为.
19-3【提升】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)设,利用勾股定理逆定理可得,再根据面面垂直的性质证明即可;
(2)建立如图所示空间直角坐标系,利用空间向量法求出二面角的余弦值;
详解:
解:(1)设,则,
∴,∴.
∵平面平面,平面平面,
∴平面.
(2)取中点O,连接,
∵,∴,∴平面,
建立如图所示空间直角坐标系,设,则,
,
设平面的法向量为,则,取可得,
设平面的法向量为,则,取可得,
所以,
由图可得二面角为钝角,∴二面角的余弦值为.
19-4【提升】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)根据题意证明平面可得,再结合即可证明平面;
(2)结合(1),以,,所在直线分别为轴,轴和轴,建立空间直角坐标系,利用坐标法求解即可.
详解:
解:(1)证明:∵在菱形ABCD中,∠BAD=60,DEAB于点E
∴,,∴.
又∵,,
∴平面,∴.
又∵,,
∴平面.
(2)∵平面,,
∴以,,所在直线分别为轴,轴和轴,建立空间直角坐标系(如图).
易知,则,,,,
∴,,
易知平面的一个法向量为.
设平面的法向量为,
由,,得,令,得,
∴.
由图得二面角为钝二面角,
∴二面角的余弦值为.
19-5【基础】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)证明,,则平面即得证;
(2)取中点为E,连结,,证明平面,以E为坐标原点,,,分别为x,y,z轴,建立空间直角坐标系,利用向量法求解即可.
详解:
(1)由,则有,又D为的中点,所以,
由,则有,,
又,
所以,
则可知,
又有,平面,所以平面;
(2)取中点为E,连结,,
由,则有,
又易知,
则有,所以,
又可知,,平面,则平面,
如图,以E为坐标原点,,,分别为x,y,z轴,建立空间直角坐标系,
有,,,,,
由,则有平面,
所以,
又,,
所以平面,
所以平面的法向量为,
设平面的法向量为,
则有,即,
可取,
记二面角为,
则.
故二面角的余弦值为.
19-6【巩固】 【正确答案】 (1)证明见解析;(2).
【试题解析】 分析:
(1)连接交于点O,连接、,先证明平面,再由三角形中位线定理得到,即可证明平面.
(2)以分别为x轴,y轴,z轴正方向建立空间直角坐标系,设,用向量法求二面角的余弦值.
详解:
(1)连接交于点O,连接、,
因为为等边三角形,所以,
因为底面为正方形,所以,
因为,所以平面,
又平面,所以,
因为平面平面,平面平面,
所以平面,
因为E为中点,所以,则平面.
(2)如图,以分别为x轴,y轴,z轴正方向建立空间直角坐标系,设,则,
所以,,,,
则,,,
因为平面平面,且平面平面=BD,,
所以面EBD,
所以平面的法向量为,
设平面的法向量为,则,
所以,不妨设x=1,所以,
所以,
显然二面角的平面角为锐角或直角,
所以二面角的余弦值为.
20-1【提升】 【正确答案】 (1);(2)证明见解析.
【试题解析】 分析:
(1)求得交点坐标为,利用两点之间的距离公式即可得解;
(2)由直线与抛物线联立可求得,,结合已知条件可知,利用点斜式可知直线的方程为,即可证得结论.
详解:
(1)联立,得,即交点坐标为,
所以,,
抛物线的标准方程为
(2)证明:设,,
将代入抛物线方程得,所以,.
设直线,同理,,
因为与直线关于直线对称,由图形对称性,计算可得.
所以,,
又,
所以直线的方程为,
化简有,所以恒过定.
点睛:
思路点睛:解决直线与抛物线的综合问题时,要注意:
(1)注意观察应用题设中的每一个条件,明确确定直线、抛物线的条件;
(2)强化有关直线与抛物线联立得出一元二次方程后的运算能力,重视根与系数之间的关系、弦长、斜率、三角形的面积等问题.
20-2【巩固】 【正确答案】 (1);(2)①;②.
【试题解析】 分析:
(1)可设出点的坐标,由直线,过作直线的垂线,垂足为点,则,则我们根据,构造出一个关于,的方程,化简后,即可得到所求曲线的方程;
(2)①由过点的直线交轨迹于、两点,交直线于点,我们可以设出直线的点斜式方程,联立直线方程后,利用设而不求的思想,结合一元二次方程根与系数关系,易求的值.
②根据平面向量数量积的性质,结合基本不等式进行求解即可.
详解:
(1)设点,则,由,
得, 化简得曲线的方程为;
(2)由于直线不能垂直于轴,且又过轴上的定点,
设直线的方程为,则 ,
设,,联立方程组
消去得,,故
由,,得
利用对应的纵坐标相等,得,,整理得,,
所以.
②因为,,所以有:由上可知: ,
因此有,
所以,当且仅当时取等号,即当时取等号,
因此.
点睛:
关键点睛:结合基本不等式,利用平面向量数量积的运算性质是解题的关键.
20-3【提升】 【正确答案】 (1);(2)存在
【试题解析】 分析:
(1)根据焦距和椭圆的几何意义即可求出椭
同课章节目录
