2.4分割面积法求二次函数最值问题 课件(共17张PPT)
文档属性
| 名称 | 2.4分割面积法求二次函数最值问题 课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 10:17:45 | ||
图片预览


文档简介
(共17张PPT)
用分割面积法求二次函数动点面积最值
北师大版 九年级下
学习目标
用分割面积法求二次函数动点面积最值
能够根据二次函数中不同图形的特点选择合适的方法解答图形的面积。
掌握利用二次函数的解析式求出相关点的坐标,从而得出相关线段的长度,利用水平宽和铅垂高方法求图形面积。
学前准备
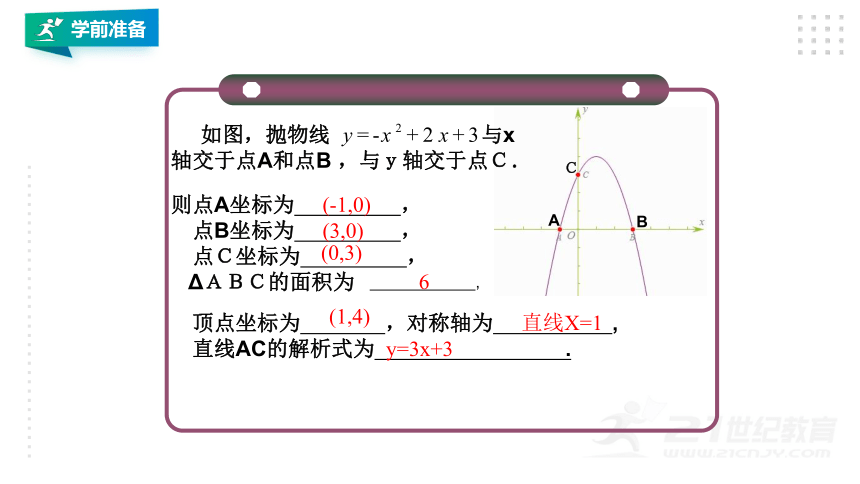
如图,抛物线 与x轴交于点A和点B ,与y轴交于点C.
则点A坐标为 ,
点B坐标为 ,
点C坐标为 ,
ΔABC的面积为
,
顶点坐标为 ,对称轴为 ,
直线AC的解析式为 .
A
B
C
(-1,0)
(3,0)
(0,3)
6
(1,4)
直线X=1
y=3x+3
合作探究1
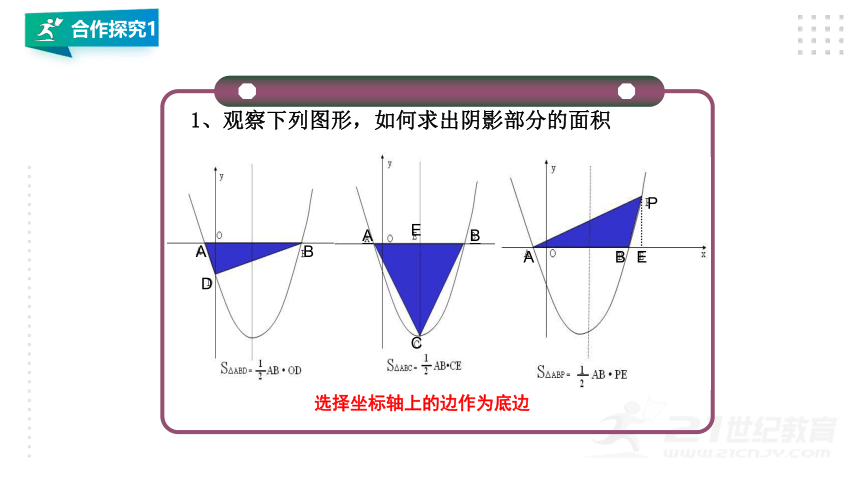
1、观察下列图形,如何求出阴影部分的面积
选择坐标轴上的边作为底边
A
B
D
A
B
C
E
A
B
P
E
例题讲解1
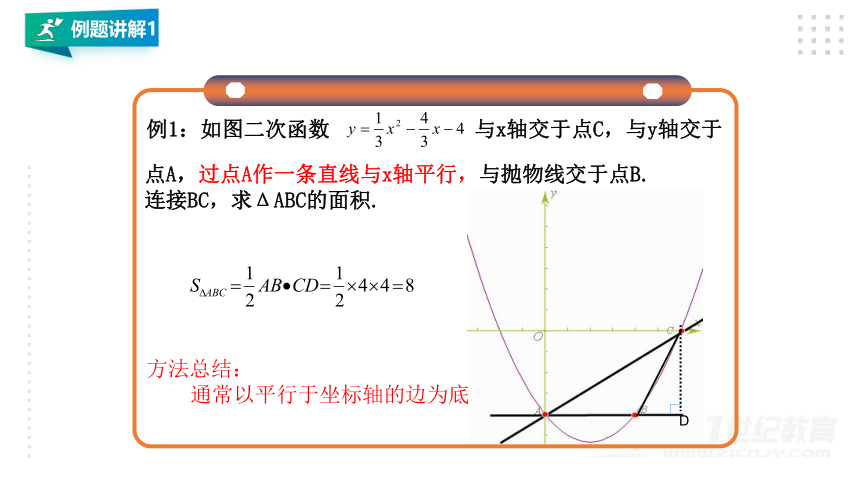
例1:如图二次函数
点A,过点A作一条直线与x轴平行,与抛物线交于点B.
连接BC,求ΔABC的面积.
与x轴交于点C,与y轴交于
D
方法总结:
通常以平行于坐标轴的边为底
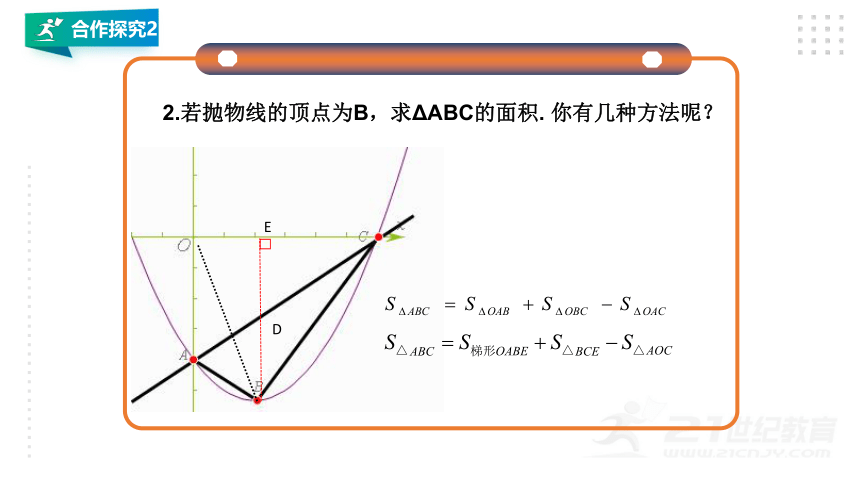
2.若抛物线的顶点为B,求ΔABC的面积. 你有几种方法呢?
D
E
合作探究2
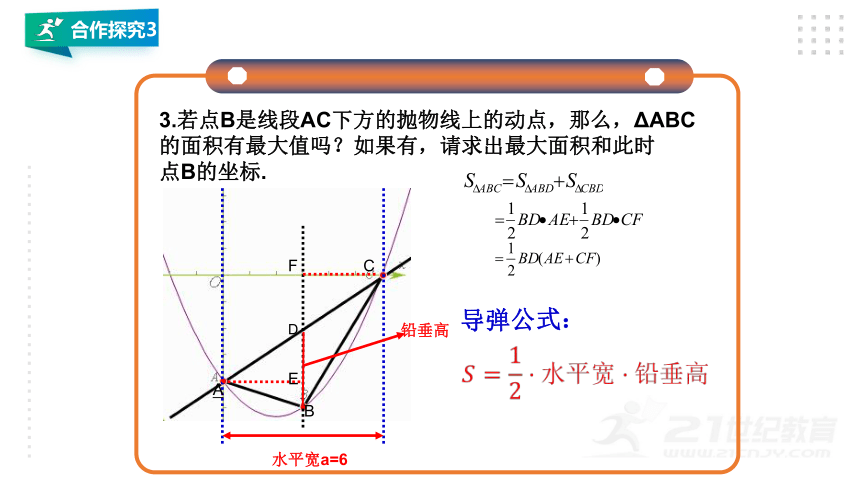
合作探究3
D
水平宽a=6
A
B
C
导弹公式:
铅垂高
3.若点B是线段AC下方的抛物线上的动点,那么,ΔABC
的面积有最大值吗?如果有,请求出最大面积和此时
点B的坐标.
E
F
例2:若点B是线段AC下方的抛物线 上的动点,如果三角形ABC有最大面积,请求出最大面积和此时点B的坐标;如果没有,
请说明理由.
D
水平宽a=6
A
B
C
例题讲解2
例题讲解2
B(3,-5)
解:在 中,令x=0,得y=-4 ∴ A(0,-4)
令y=0,即 =0,解得:x=-2或x=6 ∴C(6,0)
则直线AC:
铅锤法:
分三步走:
(1)过动点做铅垂线,交另外两个定点连成的线段于一点
(2)设出点的坐标,表示线段长
(3)利用二次函数配方求最值
归纳总结
函数中动点
图形与面积
静态
动态
规则:用公式
不规则
规则
不规则
以静代动
转化(割补法)
关键
用含x的代数式表示
相关线段的长度
学后反思
1.若抛物线
与x轴交于A、B两点,则AB= ,
与y轴交于点C,则C点的坐标为 ,
2.已知二次函数
与x轴交于A、B两点,顶点为C,
则△ABC的面积为 .
则△ABC的面积为 .
自我检测
3.已知抛物线
与y轴交于点C,直线y=x+1与抛物线交于E,F两点.点P是直线EF
下方抛物线上的动点,求△PEF
面积的最大值及点P的坐标.
与x轴交于A(-3,0),B(1,0)两点,
自我检测
4.(2016 自贡)如图,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=1/2.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
【解题思路,技巧套路】
(1)利用已知条件求出点B的坐标,然后用待定系数法求出抛物线的解析式; (2)首先求出四边形BMCA面积的表达式,然后利用二次函数的性质求出其最大值;
自我检测
相信认真学习的你一定有所收获
本节课结束
https://www.21cnjy.com/help/help_extract.php
用分割面积法求二次函数动点面积最值
北师大版 九年级下
学习目标
用分割面积法求二次函数动点面积最值
能够根据二次函数中不同图形的特点选择合适的方法解答图形的面积。
掌握利用二次函数的解析式求出相关点的坐标,从而得出相关线段的长度,利用水平宽和铅垂高方法求图形面积。
学前准备
如图,抛物线 与x轴交于点A和点B ,与y轴交于点C.
则点A坐标为 ,
点B坐标为 ,
点C坐标为 ,
ΔABC的面积为
,
顶点坐标为 ,对称轴为 ,
直线AC的解析式为 .
A
B
C
(-1,0)
(3,0)
(0,3)
6
(1,4)
直线X=1
y=3x+3
合作探究1
1、观察下列图形,如何求出阴影部分的面积
选择坐标轴上的边作为底边
A
B
D
A
B
C
E
A
B
P
E
例题讲解1
例1:如图二次函数
点A,过点A作一条直线与x轴平行,与抛物线交于点B.
连接BC,求ΔABC的面积.
与x轴交于点C,与y轴交于
D
方法总结:
通常以平行于坐标轴的边为底
2.若抛物线的顶点为B,求ΔABC的面积. 你有几种方法呢?
D
E
合作探究2
合作探究3
D
水平宽a=6
A
B
C
导弹公式:
铅垂高
3.若点B是线段AC下方的抛物线上的动点,那么,ΔABC
的面积有最大值吗?如果有,请求出最大面积和此时
点B的坐标.
E
F
例2:若点B是线段AC下方的抛物线 上的动点,如果三角形ABC有最大面积,请求出最大面积和此时点B的坐标;如果没有,
请说明理由.
D
水平宽a=6
A
B
C
例题讲解2
例题讲解2
B(3,-5)
解:在 中,令x=0,得y=-4 ∴ A(0,-4)
令y=0,即 =0,解得:x=-2或x=6 ∴C(6,0)
则直线AC:
铅锤法:
分三步走:
(1)过动点做铅垂线,交另外两个定点连成的线段于一点
(2)设出点的坐标,表示线段长
(3)利用二次函数配方求最值
归纳总结
函数中动点
图形与面积
静态
动态
规则:用公式
不规则
规则
不规则
以静代动
转化(割补法)
关键
用含x的代数式表示
相关线段的长度
学后反思
1.若抛物线
与x轴交于A、B两点,则AB= ,
与y轴交于点C,则C点的坐标为 ,
2.已知二次函数
与x轴交于A、B两点,顶点为C,
则△ABC的面积为 .
则△ABC的面积为 .
自我检测
3.已知抛物线
与y轴交于点C,直线y=x+1与抛物线交于E,F两点.点P是直线EF
下方抛物线上的动点,求△PEF
面积的最大值及点P的坐标.
与x轴交于A(-3,0),B(1,0)两点,
自我检测
4.(2016 自贡)如图,已知抛物线y=ax2+bx-2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=1/2.
(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
【解题思路,技巧套路】
(1)利用已知条件求出点B的坐标,然后用待定系数法求出抛物线的解析式; (2)首先求出四边形BMCA面积的表达式,然后利用二次函数的性质求出其最大值;
自我检测
相信认真学习的你一定有所收获
本节课结束
https://www.21cnjy.com/help/help_extract.php
