人教版数学八年级上册《11.2.1三角形内角和定理》教案
文档属性
| 名称 | 人教版数学八年级上册《11.2.1三角形内角和定理》教案 |  | |
| 格式 | docx | ||
| 文件大小 | 69.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 11:06:35 | ||
图片预览

文档简介
《11.2.1三角形内角和定理》教学设计
人教版数学八年级上册
教学目标:
知识与技能:让学生掌握三角形内角和定理及其推导过程,学会运用该定理解决实际问题。为后面学习多边形内角和规律打好基础。
过程与方法:通过动手撕拼、作图推导等方法,让学生掌握定理探究过程,向学生渗透“转化”数学思想。学习探究的一般方法和思想。
情感态度与价值观:通过分组提高同学的团队合作一时,享受自主探究得出结论的喜悦感,激发学习兴趣。
教学重点:探究三角形内角和的规律,让学生学会实际运用知识。
教学难点:使学生理解内角和的规律,掌握实际操作验证过程。
课前准备:每个学生准备好二个由硬纸片剪出的三角形
教学过程:
激趣引入
1、认识三角形内角:
引导学生观察以上三角形有几个角?三角形的这三个角,就叫做三角形的三个内角。三角形三个内角的度数和叫做三角形的内角和(引出内角和概念)。
2、三角形兄弟之争:
红色的大三角形对蓝色的小三角形说:“我比你大,所以我的内角和肯定比你大。”
小三角形不服气地说:“不对不对,我的内角和和你的一样大!”
同学们,你们知道它们中谁说得对吗?
那三角形内角和有什么规律呢,是等于多少呢?(学生根据小学知识回答180度)为什么 是不是所有三角形内角和都等于180度?接下来我们就一起来猜想验证一下这个问题。
(二)探索三角形内角和定理
1、做一做
方法:度量、剪拼图、折叠
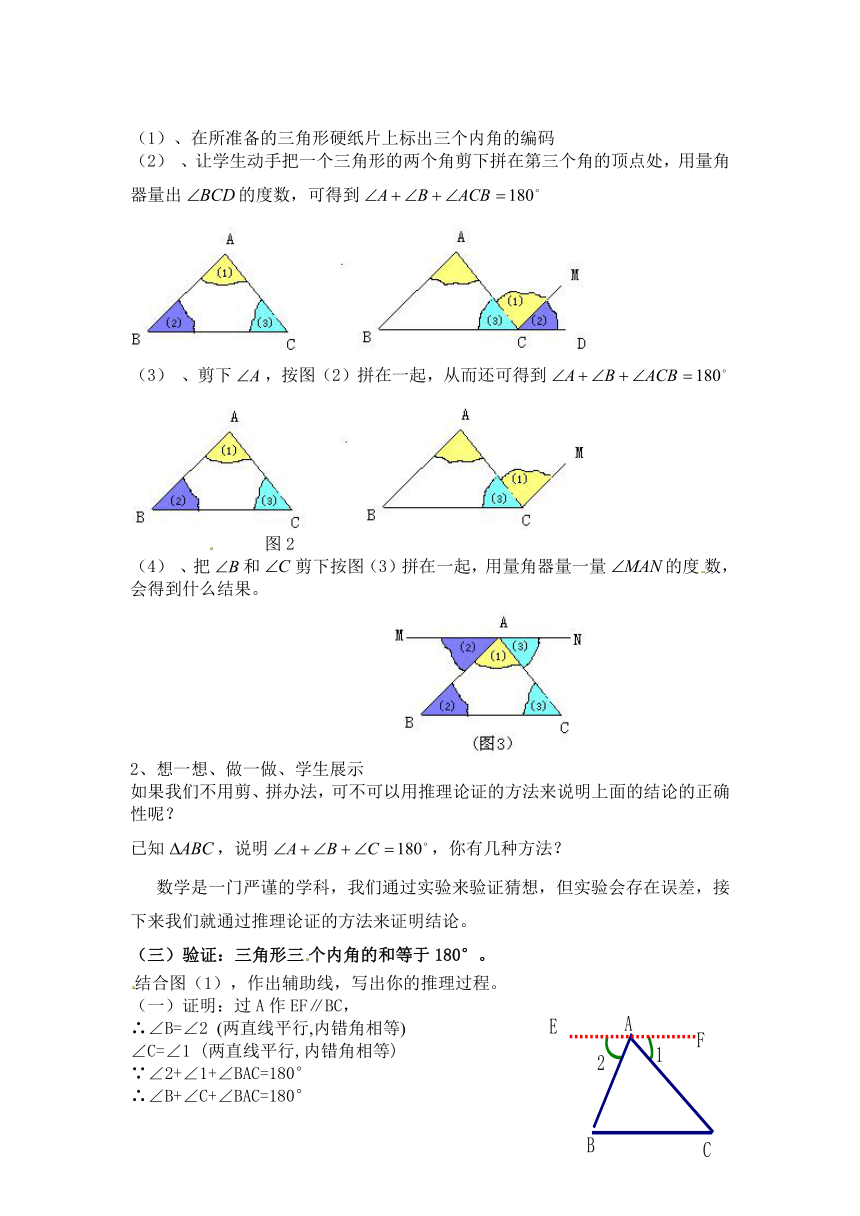
(1)、在所准备的三角形硬纸片上标出三个内角的编码
(2) 、让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出的度数,可得到
(3) 、剪下,按图(2)拼在一起,从而还可得到
图2
(4) 、把和剪下按图(3)拼在一起,用量角器量一量的度数,会得到什么结果。
2、想一想、做一做、学生展示
如果我们不用剪、拼办法,可不可以用推理论证的方法来说明上面的结论的正确性呢?
已知,说明,你有几种方法?
数学是一门严谨的学科,我们通过实验来验证猜想,但实验会存在误差,接下来我们就通过推理论证的方法来证明结论。
(三)验证:三角形三个内角的和等于180°。
结合图(1),作出辅助线,写出你的推理过程。
(一)证明:过A作EF∥BC,
∴∠B=∠2 (两直线平行,内错角相等)
∠C=∠1 (两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
结合图(2),作出辅助线,写出你的推理过程。
(二)证明:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1 (两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
结合图(3)
(三)证明:过A作AE∥BC,
∴∠B=∠BAE(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
三角形内角和定理:_____________________________________。
归纳:同学们的实验可以得出三角形内角和等于180°这个结论。
总结:三角形三个内角的和等于180°。
(板书:三角形内角和定理)
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
(四)巩固练习,解决问题
课堂练习
1、如图,说出各图中∠1 的度数.
2、(口答)下列各组角是同一个三角形的内角吗 为什么
(1)3°, 150°, 27°
(2)60°, 40°, 90°
(3)30°, 60°, 50°
例1:如图,在△ABC中∠BAC=40°, ∠ B=75°,AD是△ABC的角平分线,求∠ADB的度数。
解:∵∠BAC=40°,AD是△ABC的角平分线
∴ ∠ADB=180°-∠B-∠BAD
=180°-75°-20°=85°
3、应用新知
(1)在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= .
(3)一个三角形中最多有 个直角?为什么?
(4)一个三角形中最多有 个钝角?为什么?
(5)一个三角形中至少有 个锐角?为什么?
4、中考链接
如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是
5、课堂小测
1、在△ABC中∠B=3∠A,∠C=5∠A,求∠A、∠B、∠C的度数。
2、在△ABC中, ∠A :∠B:∠C=1:2:3,则这个三角形是 三角形。
3、如图,AB//CD,AC与BD相交于点O,∠A=30°,∠,COD=105°,则∠D的大小是( )
A、30° B、45° C、65° D、75°
总结全堂,引导反思。
哪些知识?是怎样获取这些知识的?你感觉学得怎么样?
今天你学到了:
1、三角形的内角和:三角形三个内角之和为180°
2、由三角形内角和等于180°,可得出
(1)一个三角形最多有一个直角或钝角;
(2)任意一个三角形中,最多有三个锐角,最少有两个锐角;
总结全堂,让学生清晰思路,理解猜想验证这一数学思维过程。强调本节课要点和难点。
人教版数学八年级上册
教学目标:
知识与技能:让学生掌握三角形内角和定理及其推导过程,学会运用该定理解决实际问题。为后面学习多边形内角和规律打好基础。
过程与方法:通过动手撕拼、作图推导等方法,让学生掌握定理探究过程,向学生渗透“转化”数学思想。学习探究的一般方法和思想。
情感态度与价值观:通过分组提高同学的团队合作一时,享受自主探究得出结论的喜悦感,激发学习兴趣。
教学重点:探究三角形内角和的规律,让学生学会实际运用知识。
教学难点:使学生理解内角和的规律,掌握实际操作验证过程。
课前准备:每个学生准备好二个由硬纸片剪出的三角形
教学过程:
激趣引入
1、认识三角形内角:
引导学生观察以上三角形有几个角?三角形的这三个角,就叫做三角形的三个内角。三角形三个内角的度数和叫做三角形的内角和(引出内角和概念)。
2、三角形兄弟之争:
红色的大三角形对蓝色的小三角形说:“我比你大,所以我的内角和肯定比你大。”
小三角形不服气地说:“不对不对,我的内角和和你的一样大!”
同学们,你们知道它们中谁说得对吗?
那三角形内角和有什么规律呢,是等于多少呢?(学生根据小学知识回答180度)为什么 是不是所有三角形内角和都等于180度?接下来我们就一起来猜想验证一下这个问题。
(二)探索三角形内角和定理
1、做一做
方法:度量、剪拼图、折叠
(1)、在所准备的三角形硬纸片上标出三个内角的编码
(2) 、让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出的度数,可得到
(3) 、剪下,按图(2)拼在一起,从而还可得到
图2
(4) 、把和剪下按图(3)拼在一起,用量角器量一量的度数,会得到什么结果。
2、想一想、做一做、学生展示
如果我们不用剪、拼办法,可不可以用推理论证的方法来说明上面的结论的正确性呢?
已知,说明,你有几种方法?
数学是一门严谨的学科,我们通过实验来验证猜想,但实验会存在误差,接下来我们就通过推理论证的方法来证明结论。
(三)验证:三角形三个内角的和等于180°。
结合图(1),作出辅助线,写出你的推理过程。
(一)证明:过A作EF∥BC,
∴∠B=∠2 (两直线平行,内错角相等)
∠C=∠1 (两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
结合图(2),作出辅助线,写出你的推理过程。
(二)证明:延长BC到D,过C作CE∥BA,
∴ ∠A=∠1 (两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
结合图(3)
(三)证明:过A作AE∥BC,
∴∠B=∠BAE(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°(两直线平行,同旁内角互补)
∴∠B+∠C+∠BAC=180°
三角形内角和定理:_____________________________________。
归纳:同学们的实验可以得出三角形内角和等于180°这个结论。
总结:三角形三个内角的和等于180°。
(板书:三角形内角和定理)
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
(四)巩固练习,解决问题
课堂练习
1、如图,说出各图中∠1 的度数.
2、(口答)下列各组角是同一个三角形的内角吗 为什么
(1)3°, 150°, 27°
(2)60°, 40°, 90°
(3)30°, 60°, 50°
例1:如图,在△ABC中∠BAC=40°, ∠ B=75°,AD是△ABC的角平分线,求∠ADB的度数。
解:∵∠BAC=40°,AD是△ABC的角平分线
∴ ∠ADB=180°-∠B-∠BAD
=180°-75°-20°=85°
3、应用新知
(1)在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= .
(3)一个三角形中最多有 个直角?为什么?
(4)一个三角形中最多有 个钝角?为什么?
(5)一个三角形中至少有 个锐角?为什么?
4、中考链接
如图,点O是△ABC的两条角平分线的交点,若∠BOC=118°,则∠A的大小是
5、课堂小测
1、在△ABC中∠B=3∠A,∠C=5∠A,求∠A、∠B、∠C的度数。
2、在△ABC中, ∠A :∠B:∠C=1:2:3,则这个三角形是 三角形。
3、如图,AB//CD,AC与BD相交于点O,∠A=30°,∠,COD=105°,则∠D的大小是( )
A、30° B、45° C、65° D、75°
总结全堂,引导反思。
哪些知识?是怎样获取这些知识的?你感觉学得怎么样?
今天你学到了:
1、三角形的内角和:三角形三个内角之和为180°
2、由三角形内角和等于180°,可得出
(1)一个三角形最多有一个直角或钝角;
(2)任意一个三角形中,最多有三个锐角,最少有两个锐角;
总结全堂,让学生清晰思路,理解猜想验证这一数学思维过程。强调本节课要点和难点。
