24.1.1 圆 人教版九年级数学上册课时作业(含答案)
文档属性
| 名称 | 24.1.1 圆 人教版九年级数学上册课时作业(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 338.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 12:21:04 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级数学上册课时作业
第二十四章 圆
24.1.1 圆
1. 到定点的距离等于定长的点的集合是( )
A.圆的外部 B.圆的内部 C.圆 D.圆的内部和圆
2. 如图是一个由四个同心圆构成的靶子示意图,点O为圆心,且OA=AB=BC=CD=5,那么周长最接近100的圆是( )
A.以OA为半径的圆 B.以OB为半径的圆
C.以OC为半径的圆 D.以OD为半径的圆
3. 下列说法错误的是( )
A.半径相等的两个圆是等圆 B.圆中最长的弦有无数条
C.长度相等的两条弧是等弧 D.半圆是一条弧
4. 已知AB是直径为10的圆的一条弦,则AB的长度不可能是( )
A.2 B.5 C.9 D.11
5. 已知点C在线段AB上(点C与点A,B不重合),过点A,B的圆记作☉O1,过点B,C的圆记作☉O2,过点C,A的圆记作☉O3,则下列说法中正确的是( )
A.☉O1可以经过点C B.点C可以在☉O1的内部
C.点A可以在☉O2的内部 D.点B可以在☉O3的内部
6. 下列各图形中,各个顶点一定在同一个圆上的是( )
A.正方形 B.菱形 C.平行四边形 D.梯形
7. 如图,奥迪车商标的长为34 cm、宽为10 cm,则d的值为( )
A.14 cm B.16 cm C.18 cm D.20 cm
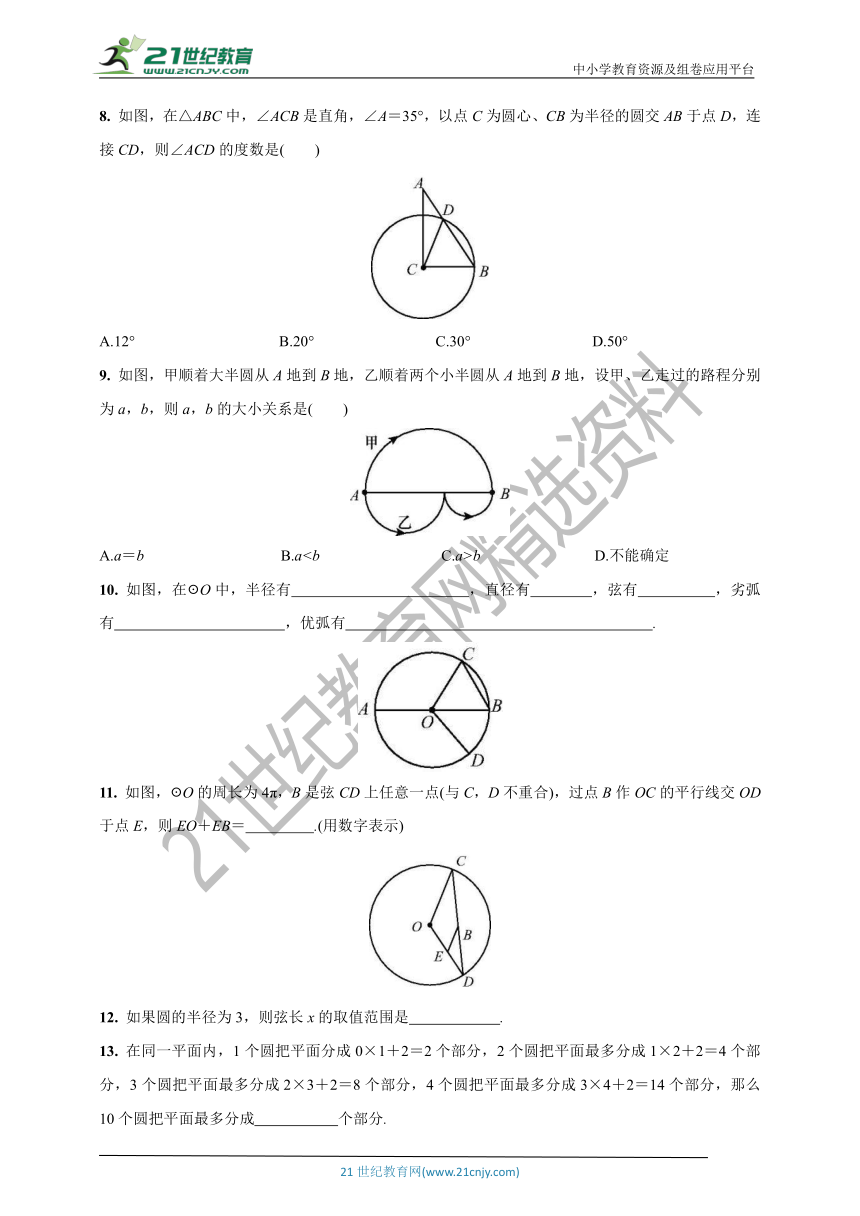
8. 如图,在△ABC中,∠ACB是直角,∠A=35°,以点C为圆心、CB为半径的圆交AB于点D,连接CD,则∠ACD的度数是( )
A.12° B.20° C.30° D.50°
9. 如图,甲顺着大半圆从A地到B地,乙顺着两个小半圆从A地到B地,设甲、乙走过的路程分别为a,b,则a,b的大小关系是( )
A.a=b B.ab D.不能确定
10. 如图,在☉O中,半径有 ,直径有 ,弦有 ,劣弧有 ,优弧有 .
11. 如图,☉O的周长为4π,B是弦CD上任意一点(与C,D不重合),过点B作OC的平行线交OD于点E,则EO+EB= .(用数字表示)
12. 如果圆的半径为3,则弦长x的取值范围是 .
13. 在同一平面内,1个圆把平面分成0×1+2=2个部分,2个圆把平面最多分成1×2+2=4个部分,3个圆把平面最多分成2×3+2=8个部分,4个圆把平面最多分成3×4+2=14个部分,那么10个圆把平面最多分成 个部分.
14. 已知点P,Q,且PQ=4 cm.
(1)画出下列图形:到点P的距离等于2 cm的点的集合;到点Q的距离等于3 cm的点的集合.
(2)在所画图中,到点P的距离等于2 cm,且到点Q的距离等于3 cm的点有几个 请在图中将它们表示出来.
15. 如图,在☉O中,AB为弦,C,D两点在AB上,且AC=BD.求证:∠AOC=∠BOD.
16. 如图,AB,CD为☉O中的两条直径,点E,F在直径CD上,且CE=DF.求证:AF=BE.
17. 如图,点P(x,y)在以坐标原点为圆心、5为半径的圆上.若x,y都是整数,请探究这样的点P一共有多少个 写出这些点的坐标.
18. 如图,AB是☉O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么☉O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长l2= ;
(2)把AB分成三条相等的线段,每个小圆的周长l3= ;
(3)把AB分成四条相等的线段,每个小圆的周长l4= ;
(4)把AB分成n条相等的线段,每个小圆的周长ln= .
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的 .请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
参 考 答 案
1. C 2. C 3. C 4. D 5. B 6. A 7. C 8. B 9. A
10. OA,OB,OC,OD AB AB,BC ,,,, ,,,,
11. 2
12. 013. 92
14. 解:(1)图略.
(2)到点P的距离等于2 cm,且到点Q的距离等于3 cm的点有2个.图略.
15. 证明:∵OA=OB,∴∠A=∠B. 在△OAC和△OBD中, ∴△OAC≌△OBD(SAS),∴∠AOC=∠BOD.
16. 证明:由题意得OA=OB,OC=OD. ∵CE=DF,∴OF=OE,又∵∠AOF=∠BOE,∴△AOF≌△BOE(SAS),∴AF=BE.
17. 解:分为两种情况:①若这个点在坐标轴上,那么有4个,它们是(0,5),(5,0),(-5,0),(0,-5);②若这个点在象限内,∵52=42+32,而P都是整数点,∴这样的点有8个,分别是(3,4),(-3,4),(3,-4),(-3,-4),(4,3),(-4,3),(4,-3),(-4,-3). ∴这样的点P一共有12个.
解:(1)πa
(2)πa
(3)πa
(4)πa 每个小圆面积=π(·a)2=·,而大圆的面积=π(·a)2=πa2.
即每个小圆面积是大圆面积的.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学上册课时作业
第二十四章 圆
24.1.1 圆
1. 到定点的距离等于定长的点的集合是( )
A.圆的外部 B.圆的内部 C.圆 D.圆的内部和圆
2. 如图是一个由四个同心圆构成的靶子示意图,点O为圆心,且OA=AB=BC=CD=5,那么周长最接近100的圆是( )
A.以OA为半径的圆 B.以OB为半径的圆
C.以OC为半径的圆 D.以OD为半径的圆
3. 下列说法错误的是( )
A.半径相等的两个圆是等圆 B.圆中最长的弦有无数条
C.长度相等的两条弧是等弧 D.半圆是一条弧
4. 已知AB是直径为10的圆的一条弦,则AB的长度不可能是( )
A.2 B.5 C.9 D.11
5. 已知点C在线段AB上(点C与点A,B不重合),过点A,B的圆记作☉O1,过点B,C的圆记作☉O2,过点C,A的圆记作☉O3,则下列说法中正确的是( )
A.☉O1可以经过点C B.点C可以在☉O1的内部
C.点A可以在☉O2的内部 D.点B可以在☉O3的内部
6. 下列各图形中,各个顶点一定在同一个圆上的是( )
A.正方形 B.菱形 C.平行四边形 D.梯形
7. 如图,奥迪车商标的长为34 cm、宽为10 cm,则d的值为( )
A.14 cm B.16 cm C.18 cm D.20 cm
8. 如图,在△ABC中,∠ACB是直角,∠A=35°,以点C为圆心、CB为半径的圆交AB于点D,连接CD,则∠ACD的度数是( )
A.12° B.20° C.30° D.50°
9. 如图,甲顺着大半圆从A地到B地,乙顺着两个小半圆从A地到B地,设甲、乙走过的路程分别为a,b,则a,b的大小关系是( )
A.a=b B.ab D.不能确定
10. 如图,在☉O中,半径有 ,直径有 ,弦有 ,劣弧有 ,优弧有 .
11. 如图,☉O的周长为4π,B是弦CD上任意一点(与C,D不重合),过点B作OC的平行线交OD于点E,则EO+EB= .(用数字表示)
12. 如果圆的半径为3,则弦长x的取值范围是 .
13. 在同一平面内,1个圆把平面分成0×1+2=2个部分,2个圆把平面最多分成1×2+2=4个部分,3个圆把平面最多分成2×3+2=8个部分,4个圆把平面最多分成3×4+2=14个部分,那么10个圆把平面最多分成 个部分.
14. 已知点P,Q,且PQ=4 cm.
(1)画出下列图形:到点P的距离等于2 cm的点的集合;到点Q的距离等于3 cm的点的集合.
(2)在所画图中,到点P的距离等于2 cm,且到点Q的距离等于3 cm的点有几个 请在图中将它们表示出来.
15. 如图,在☉O中,AB为弦,C,D两点在AB上,且AC=BD.求证:∠AOC=∠BOD.
16. 如图,AB,CD为☉O中的两条直径,点E,F在直径CD上,且CE=DF.求证:AF=BE.
17. 如图,点P(x,y)在以坐标原点为圆心、5为半径的圆上.若x,y都是整数,请探究这样的点P一共有多少个 写出这些点的坐标.
18. 如图,AB是☉O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么☉O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长l2= ;
(2)把AB分成三条相等的线段,每个小圆的周长l3= ;
(3)把AB分成四条相等的线段,每个小圆的周长l4= ;
(4)把AB分成n条相等的线段,每个小圆的周长ln= .
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的 .请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
参 考 答 案
1. C 2. C 3. C 4. D 5. B 6. A 7. C 8. B 9. A
10. OA,OB,OC,OD AB AB,BC ,,,, ,,,,
11. 2
12. 0
14. 解:(1)图略.
(2)到点P的距离等于2 cm,且到点Q的距离等于3 cm的点有2个.图略.
15. 证明:∵OA=OB,∴∠A=∠B. 在△OAC和△OBD中, ∴△OAC≌△OBD(SAS),∴∠AOC=∠BOD.
16. 证明:由题意得OA=OB,OC=OD. ∵CE=DF,∴OF=OE,又∵∠AOF=∠BOE,∴△AOF≌△BOE(SAS),∴AF=BE.
17. 解:分为两种情况:①若这个点在坐标轴上,那么有4个,它们是(0,5),(5,0),(-5,0),(0,-5);②若这个点在象限内,∵52=42+32,而P都是整数点,∴这样的点有8个,分别是(3,4),(-3,4),(3,-4),(-3,-4),(4,3),(-4,3),(4,-3),(-4,-3). ∴这样的点P一共有12个.
解:(1)πa
(2)πa
(3)πa
(4)πa 每个小圆面积=π(·a)2=·,而大圆的面积=π(·a)2=πa2.
即每个小圆面积是大圆面积的.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
