不等式和绝对值不等式
图片预览









文档简介
(共47张PPT)
第一讲 不等式和绝对值不等式
1、不等式
1、不等式的基本性质:
①、对称性: 传递性:_________
②、 ,a+c>b+c
③、a>b, , 那么ac>bc;
a>b, ,那么ac<bc
④、a>b>0, 那么,ac>bd
⑤、a>b>0,那么an>bn.(条件 )
⑥、 a>b>0 那么 (条件 )
练习:1、判断下列各命题的真假,并说明理由:
(1)如果a>b,那么ac>bc;
(2)如果a>b,那么ac2>bc2;
(3)如果a>b,那么an>bn(n∈N+);
(4)如果a>b, cb-d。
2、比较(x+1)(x+2)和(x-3)(x+6)的大小。
(假命题)
(假命题)
(真命题)
(假命题)
解:因为(x+1)(x+2)-(x-3)(x+6)
=x2+3x+2-(x2+3x-18)
=20>0,
所以(x+1)(x+2)>(x-3)(x+6)
例2、 已知a>b>0,c>d>0,求证:
例1、求证:如果a>b>0,c>d>0,那么ac>bd。
证明:因为a>b>0, c>d>0,
由不等式的基本性质(3)可得ac>bc, bc>bd,
再由不等式的传递性可得ac>bc>bd。
练习: 如果a>b,c>d,是否一定能得出ac>bd?并说明理由 。
例3、若a、b、x、y∈R,则 是
成立的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
C
例5、已知f(x)=ax2+c,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围。
例4、对于实数a、b、c,判断下列命题的真假:
(1)若c>a>b>0,则
(2)若a>b, ,则a>0,b<0。
(真命题)
(真命题)
f(3)的取值范围是[-1, 20]
例6、已知a>0,a2-2ab+c2 =0,bc>a2,试比较a、b、c的大小。
解:因为bc>a2>0,所以b、c同号;又a2+c2=2ab>0,且
a>0,所以b= 且c>0。
因为(a-c)2=a2-2ac+c2=2ab-2ac=2a(b-c )≥0,所以b-c≥0.
当b-c>0,即b>c时,b= 得
所以a2c+c3 >2a3即a3-c3+a3-a2c<0,(a-c)(2a2+ac+c2)<0
因为a>0,b>0,c>0,所以2a2+ac+c2>0,故a-c<0,即a从而aa2,
所以b2>a2,即b≠a。又a2-2ab+b2=(a-b)2=0,所以a=b,
与前面矛盾,故b≠c.所以a小结:理解并掌握不等式的六个基本性质
作业:课本P10第3题。求证:
(1)如果a>b, ab>0,那么
(2)如果a>b>0,c选做题:设a≥b,c≥d,
求证:ac+bd≥ (a+b)(c+d)
2、基本不等式
定理1 如果a, b∈R, 那么
a2+b2≥2ab.
当且仅当a=b时等号成立。
探究: 你能从几何的角度解释定理1吗?
分析:a2与b2的几何意义是正方形面积,ab的几何意义是矩形面积,可考虑从图形的面积角度解释定理。
a
a
b
b
b
A
H
I
D
K
G
B
J
C
F
E
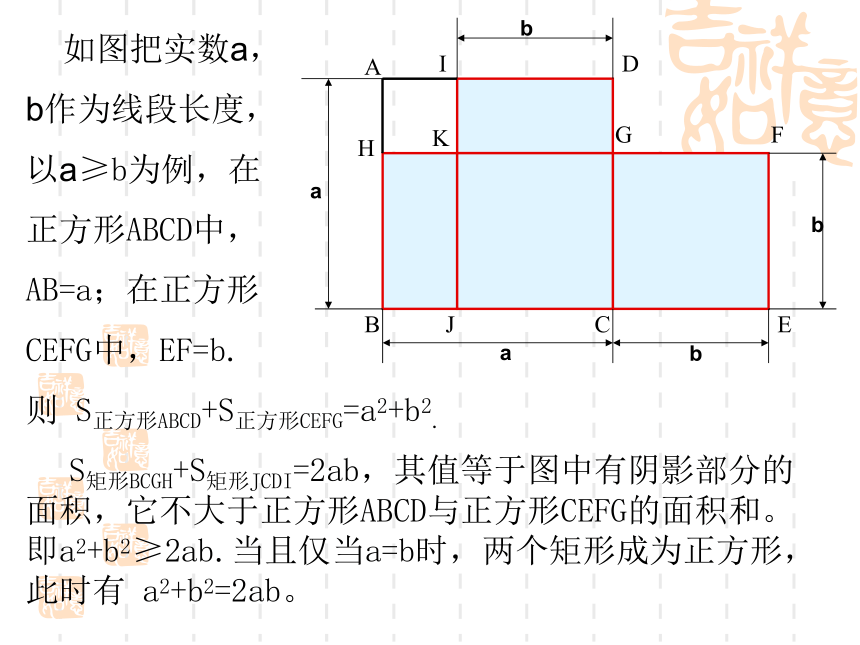
如图把实数a,
b作为线段长度,
以a≥b为例,在
正方形ABCD中,
AB=a;在正方形
CEFG中,EF=b.
则 S正方形ABCD+S正方形CEFG=a2+b2.
S矩形BCGH+S矩形JCDI=2ab,其值等于图中有阴影部分的面积,它不大于正方形ABCD与正方形CEFG的面积和。 即a2+b2≥2ab.当且仅当a=b时,两个矩形成为正方形,此时有 a2+b2=2ab。
定理2(基本不等式) 如果a,b>0,那么
当且仅当a=b时,等号成立。
证明:因为 =a+b-2 ≥0,
所以a+b≥ ,
上式当且仅当 ,即a=b时,等号成立。
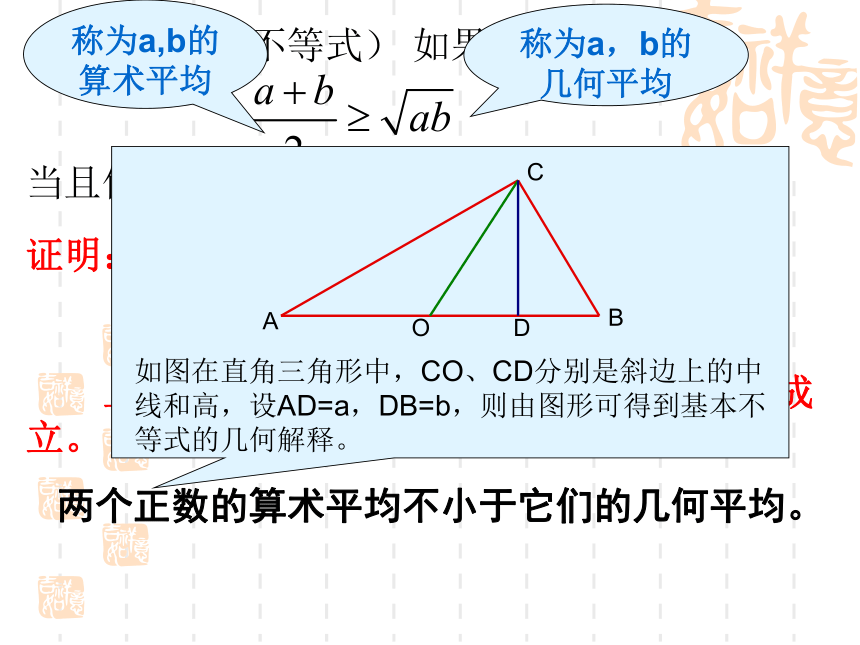
称为a,b的算术平均
称为a,b的几何平均
两个正数的算术平均不小于它们的几何平均。
如图在直角三角形中,CO、CD分别是斜边上的中线和高,设AD=a,DB=b,则由图形可得到基本不等式的几何解释。
C
A
B
D
O
例3 求证:(1)在所有周长相同的矩形中,正方形的面积最大;(2)在所有面积相同的矩形中,正方形的周长最短。
结论:已知x, y都是正数。(1)如果积xy是定值p,那么当x=y时,和x+y有最小值2 ;(2)如果和x+y是定值s,那么当x=y时,积xy有最大值
A
B
E
N
M
F
D
C
Q
P
H
G
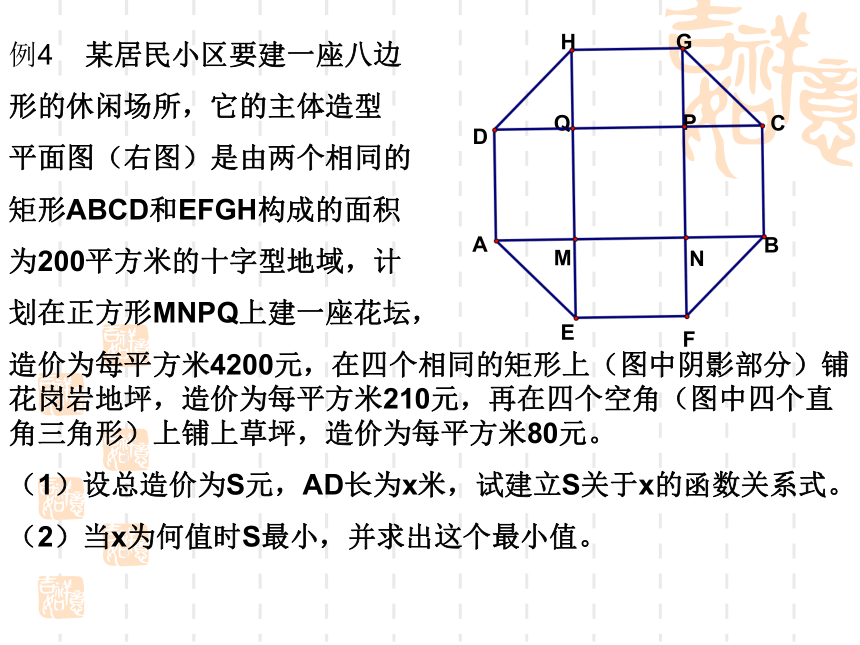
例4 某居民小区要建一座八边
形的休闲场所,它的主体造型
平面图(右图)是由两个相同的
矩形ABCD和EFGH构成的面积
为200平方米的十字型地域,计
划在正方形MNPQ上建一座花坛,
造价为每平方米4200元,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角(图中四个直角三角形)上铺上草坪,造价为每平方米80元。
(1)设总造价为S元,AD长为x米,试建立S关于x的函数关系式。
(2)当x为何值时S最小,并求出这个最小值。
课堂练习:课本P10第5题、第6题、第9题
5、设a, b∈R+,且a≠b,求证: (1) (2)
6、设a,b,c是不全相等的正数,求证:
(1)(a+b)(b+c)(c+a)>8abc;
(2)a+b+c>
9、已知x、y∈R,求证:
小结:理解并熟练掌握基本不等式及其应用,特别要注意利用基本不等式求最值时, 一定要满足“一正二定三相等”的条件。
作业:课本P10第7、8、10题,第11题为选做题。
3、三个正数的算术-几何平均不等式
练习:θ是锐角,求y=sinθcos2θ的最大值。
13、在对角线有相同长度的所有矩形中,怎样的矩形周长最长,怎样的矩形面积最大?
14、已知球的半径为R,球内球圆柱的底面半径为r,高为h,则r与 h为何值时,内接圆柱的体积最大?
二、绝对值不等式
1、绝对值三角不等式
实数a的绝对值|a|的几何意义是表示数轴上坐标为a的点A到原点的距离:
O
a
A
x
|a|
x
A
B
a
b
|a-b|
任意两个实数a,b在数轴上的对应点分别为A、B,那么|a-b|的几何意义是A、B两点间的距离。
联系绝对值的几何意义,从“运算”的角度研究|a|,|b|,|a+b|,|a-b|等之间的关系:
分ab>0和ab<0两种情形讨论:
(1)当ab>0时,如下图可得|a+b|=|a|+|b|
O
x
a
b
a+b
O
x
a
b
a+b
(2)当ab<0时,也分为两种情况:如果a>0,b<0,如下图可得:|a+b|<|a|+|b|
O
b
a
x
a+b
如果a<0, b>0,如下图可得:|a+b|<|a|+|b|
a+b
a
b
x
O
(3)如果ab=0,则a=0或b=0,易得:
|a+b|=|a|+|b|
定理1 如果a, b是实数,则
|a+b|≤|a|+|b|
当且仅当ab≥0时,等号成立。
探究 如果把定理1中的实数a, b分别换成向量a, b, 能得出什么结果?你能解释它的几何意义吗?
O
x
y
探究 当向量
a, b共线时,有怎样的结论?
这个不等式称为绝对值三角不等式。
定理1的代数证明:
探究 你能根据定理1的研究思路,探究一下|a|,|b|,|a+b|,|a-b|等之间的其他关系吗?例如:|a|-|b|与|a+b|,|a|+|b|与|a-b|,|a|-|b|与|a-b|等之间的关系。
|a|-|b|≤|a+b|,
|a|+|b|≥|a-b|,
|a|-|b|≤|a-b|.
如果a, b是实数,那么
|a|-|b|≤|a±b|≤|a|+|b|
例1 已知ε>0,|x-a|<ε,|y-b|<ε,求证:
|2x+3y-2a-3b|<5ε.
证明: |2x+3y-2a-3b|=|(2x-2a)+(3y-3b)|
=|2(x-a)+3(y-b)|≤|2(x-a)|+|3(y-b)|
=2|x-a|+3|y-b|<2ε +3ε=5ε.
所以 |2x+3y-2a-3b|<5ε.
定理2 如果a, b, c是实数,那么
|a-c|≤|a-b|+|b-c|
当且仅当(a-b)(b-c)≥0时,等号成立。
证明:根据绝对值三角不等式有
|a-c|=|(a-b)+(b-c)|≤|a-b|+|b-c|
当且仅当(a-b)(b-c)≥0时,等号成立。
B
例2 两个施工队分别被安排在公路沿线的两个地点施工,这两个地点分别位于公路路碑的第10km和第20km处。现要在公路沿线建两个施工队的共同临时生活区,每个施工队每天在生活区和施工地点之间往返一次。要使两个施工队每天往返的路程之和最小,生活区应该建于何处?
分析:假设生活区建在公路路碑的第xkm处,两个施工队每天往返的路程之和为S(x)km,则有
S(x)=2(|x-10|+|x-20|),要求问题化归为求该函数的最小值,可用绝对值三角不等式求解。
练习:课本P20第1、2题
.求证:(1)|a+b|+|a-b|≥2|a|
(2)|a+b|-|a-b|≤2|b|
2.用几种方法证明
D
D
C
小结:理解和掌握绝对值不等式的两个定理:
|a+b|≤|a|+|b|(a,b∈R,ab≥0时等号成立)
|a-c|≤|a-b|+|b-c|(a,b,c∈R,
(a-b)(b-c)≥0时等号成立)
能应用定理解决一些证明和求最值问题。
作业:课本P20第3、4、5题
2、绝对值不等式的解法
复习:如果a>0,则
|x||x|>a的解集是(-∞,-a)∪(a,+∞)
O
a
-a
x
O
-a
a
x
|x||x|>a
(1)|ax+b|≤c和|ax+b|≥c(c>0)型不等式的解法:
①换元法:令t=ax+b, 转化为|t|≤c和|t|≥c型不等式,然后再求x,得原不等式的解集。
②分段讨论法:
例3 解不等式|3x-1|≤2
例4 解不等式|2-3x|≥7
补充例题:解不等式
|ax+b|c(c>0)型不等式比较:
类型 化去绝对值后 集合上解的意义区别
|ax+b|-c-c} ∩ {x|ax+b|ax+b|>c
ax+b<-c或ax+b>c {x|ax+b<-c}∪
{x|ax+b>c}, 并
课堂练习:P20第6题
x
1
2
-2
-3
A
B
A1
B1
y
x
O
-3
2
-2
①利用绝对值不等式的几何意义
②零点分区间法
③构造函数法
作业:P20第7题、第8题(1)(3)
练习:P20第8题(2)
补充练习:解不等式:
(1)1<|2x+1|≤3.
(2)||x-1|-4|<2.
(3)|3x-1|>x+3.
答案:(1){x|0(2){x|-5(3)
作业
8.解不等式:
第一讲 不等式和绝对值不等式
1、不等式
1、不等式的基本性质:
①、对称性: 传递性:_________
②、 ,a+c>b+c
③、a>b, , 那么ac>bc;
a>b, ,那么ac<bc
④、a>b>0, 那么,ac>bd
⑤、a>b>0,那么an>bn.(条件 )
⑥、 a>b>0 那么 (条件 )
练习:1、判断下列各命题的真假,并说明理由:
(1)如果a>b,那么ac>bc;
(2)如果a>b,那么ac2>bc2;
(3)如果a>b,那么an>bn(n∈N+);
(4)如果a>b, c
2、比较(x+1)(x+2)和(x-3)(x+6)的大小。
(假命题)
(假命题)
(真命题)
(假命题)
解:因为(x+1)(x+2)-(x-3)(x+6)
=x2+3x+2-(x2+3x-18)
=20>0,
所以(x+1)(x+2)>(x-3)(x+6)
例2、 已知a>b>0,c>d>0,求证:
例1、求证:如果a>b>0,c>d>0,那么ac>bd。
证明:因为a>b>0, c>d>0,
由不等式的基本性质(3)可得ac>bc, bc>bd,
再由不等式的传递性可得ac>bc>bd。
练习: 如果a>b,c>d,是否一定能得出ac>bd?并说明理由 。
例3、若a、b、x、y∈R,则 是
成立的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
C
例5、已知f(x)=ax2+c,且-4≤f(1)≤-1,-1≤f(2)≤5,求f(3)的取值范围。
例4、对于实数a、b、c,判断下列命题的真假:
(1)若c>a>b>0,则
(2)若a>b, ,则a>0,b<0。
(真命题)
(真命题)
f(3)的取值范围是[-1, 20]
例6、已知a>0,a2-2ab+c2 =0,bc>a2,试比较a、b、c的大小。
解:因为bc>a2>0,所以b、c同号;又a2+c2=2ab>0,且
a>0,所以b= 且c>0。
因为(a-c)2=a2-2ac+c2=2ab-2ac=2a(b-c )≥0,所以b-c≥0.
当b-c>0,即b>c时,b= 得
所以a2c+c3 >2a3即a3-c3+a3-a2c<0,(a-c)(2a2+ac+c2)<0
因为a>0,b>0,c>0,所以2a2+ac+c2>0,故a-c<0,即a
所以b2>a2,即b≠a。又a2-2ab+b2=(a-b)2=0,所以a=b,
与前面矛盾,故b≠c.所以a
作业:课本P10第3题。求证:
(1)如果a>b, ab>0,那么
(2)如果a>b>0,c
求证:ac+bd≥ (a+b)(c+d)
2、基本不等式
定理1 如果a, b∈R, 那么
a2+b2≥2ab.
当且仅当a=b时等号成立。
探究: 你能从几何的角度解释定理1吗?
分析:a2与b2的几何意义是正方形面积,ab的几何意义是矩形面积,可考虑从图形的面积角度解释定理。
a
a
b
b
b
A
H
I
D
K
G
B
J
C
F
E
如图把实数a,
b作为线段长度,
以a≥b为例,在
正方形ABCD中,
AB=a;在正方形
CEFG中,EF=b.
则 S正方形ABCD+S正方形CEFG=a2+b2.
S矩形BCGH+S矩形JCDI=2ab,其值等于图中有阴影部分的面积,它不大于正方形ABCD与正方形CEFG的面积和。 即a2+b2≥2ab.当且仅当a=b时,两个矩形成为正方形,此时有 a2+b2=2ab。
定理2(基本不等式) 如果a,b>0,那么
当且仅当a=b时,等号成立。
证明:因为 =a+b-2 ≥0,
所以a+b≥ ,
上式当且仅当 ,即a=b时,等号成立。
称为a,b的算术平均
称为a,b的几何平均
两个正数的算术平均不小于它们的几何平均。
如图在直角三角形中,CO、CD分别是斜边上的中线和高,设AD=a,DB=b,则由图形可得到基本不等式的几何解释。
C
A
B
D
O
例3 求证:(1)在所有周长相同的矩形中,正方形的面积最大;(2)在所有面积相同的矩形中,正方形的周长最短。
结论:已知x, y都是正数。(1)如果积xy是定值p,那么当x=y时,和x+y有最小值2 ;(2)如果和x+y是定值s,那么当x=y时,积xy有最大值
A
B
E
N
M
F
D
C
Q
P
H
G
例4 某居民小区要建一座八边
形的休闲场所,它的主体造型
平面图(右图)是由两个相同的
矩形ABCD和EFGH构成的面积
为200平方米的十字型地域,计
划在正方形MNPQ上建一座花坛,
造价为每平方米4200元,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角(图中四个直角三角形)上铺上草坪,造价为每平方米80元。
(1)设总造价为S元,AD长为x米,试建立S关于x的函数关系式。
(2)当x为何值时S最小,并求出这个最小值。
课堂练习:课本P10第5题、第6题、第9题
5、设a, b∈R+,且a≠b,求证: (1) (2)
6、设a,b,c是不全相等的正数,求证:
(1)(a+b)(b+c)(c+a)>8abc;
(2)a+b+c>
9、已知x、y∈R,求证:
小结:理解并熟练掌握基本不等式及其应用,特别要注意利用基本不等式求最值时, 一定要满足“一正二定三相等”的条件。
作业:课本P10第7、8、10题,第11题为选做题。
3、三个正数的算术-几何平均不等式
练习:θ是锐角,求y=sinθcos2θ的最大值。
13、在对角线有相同长度的所有矩形中,怎样的矩形周长最长,怎样的矩形面积最大?
14、已知球的半径为R,球内球圆柱的底面半径为r,高为h,则r与 h为何值时,内接圆柱的体积最大?
二、绝对值不等式
1、绝对值三角不等式
实数a的绝对值|a|的几何意义是表示数轴上坐标为a的点A到原点的距离:
O
a
A
x
|a|
x
A
B
a
b
|a-b|
任意两个实数a,b在数轴上的对应点分别为A、B,那么|a-b|的几何意义是A、B两点间的距离。
联系绝对值的几何意义,从“运算”的角度研究|a|,|b|,|a+b|,|a-b|等之间的关系:
分ab>0和ab<0两种情形讨论:
(1)当ab>0时,如下图可得|a+b|=|a|+|b|
O
x
a
b
a+b
O
x
a
b
a+b
(2)当ab<0时,也分为两种情况:如果a>0,b<0,如下图可得:|a+b|<|a|+|b|
O
b
a
x
a+b
如果a<0, b>0,如下图可得:|a+b|<|a|+|b|
a+b
a
b
x
O
(3)如果ab=0,则a=0或b=0,易得:
|a+b|=|a|+|b|
定理1 如果a, b是实数,则
|a+b|≤|a|+|b|
当且仅当ab≥0时,等号成立。
探究 如果把定理1中的实数a, b分别换成向量a, b, 能得出什么结果?你能解释它的几何意义吗?
O
x
y
探究 当向量
a, b共线时,有怎样的结论?
这个不等式称为绝对值三角不等式。
定理1的代数证明:
探究 你能根据定理1的研究思路,探究一下|a|,|b|,|a+b|,|a-b|等之间的其他关系吗?例如:|a|-|b|与|a+b|,|a|+|b|与|a-b|,|a|-|b|与|a-b|等之间的关系。
|a|-|b|≤|a+b|,
|a|+|b|≥|a-b|,
|a|-|b|≤|a-b|.
如果a, b是实数,那么
|a|-|b|≤|a±b|≤|a|+|b|
例1 已知ε>0,|x-a|<ε,|y-b|<ε,求证:
|2x+3y-2a-3b|<5ε.
证明: |2x+3y-2a-3b|=|(2x-2a)+(3y-3b)|
=|2(x-a)+3(y-b)|≤|2(x-a)|+|3(y-b)|
=2|x-a|+3|y-b|<2ε +3ε=5ε.
所以 |2x+3y-2a-3b|<5ε.
定理2 如果a, b, c是实数,那么
|a-c|≤|a-b|+|b-c|
当且仅当(a-b)(b-c)≥0时,等号成立。
证明:根据绝对值三角不等式有
|a-c|=|(a-b)+(b-c)|≤|a-b|+|b-c|
当且仅当(a-b)(b-c)≥0时,等号成立。
B
例2 两个施工队分别被安排在公路沿线的两个地点施工,这两个地点分别位于公路路碑的第10km和第20km处。现要在公路沿线建两个施工队的共同临时生活区,每个施工队每天在生活区和施工地点之间往返一次。要使两个施工队每天往返的路程之和最小,生活区应该建于何处?
分析:假设生活区建在公路路碑的第xkm处,两个施工队每天往返的路程之和为S(x)km,则有
S(x)=2(|x-10|+|x-20|),要求问题化归为求该函数的最小值,可用绝对值三角不等式求解。
练习:课本P20第1、2题
.求证:(1)|a+b|+|a-b|≥2|a|
(2)|a+b|-|a-b|≤2|b|
2.用几种方法证明
D
D
C
小结:理解和掌握绝对值不等式的两个定理:
|a+b|≤|a|+|b|(a,b∈R,ab≥0时等号成立)
|a-c|≤|a-b|+|b-c|(a,b,c∈R,
(a-b)(b-c)≥0时等号成立)
能应用定理解决一些证明和求最值问题。
作业:课本P20第3、4、5题
2、绝对值不等式的解法
复习:如果a>0,则
|x|
O
a
-a
x
O
-a
a
x
|x|
(1)|ax+b|≤c和|ax+b|≥c(c>0)型不等式的解法:
①换元法:令t=ax+b, 转化为|t|≤c和|t|≥c型不等式,然后再求x,得原不等式的解集。
②分段讨论法:
例3 解不等式|3x-1|≤2
例4 解不等式|2-3x|≥7
补充例题:解不等式
|ax+b|
类型 化去绝对值后 集合上解的意义区别
|ax+b|
ax+b<-c或ax+b>c {x|ax+b<-c}∪
{x|ax+b>c}, 并
课堂练习:P20第6题
x
1
2
-2
-3
A
B
A1
B1
y
x
O
-3
2
-2
①利用绝对值不等式的几何意义
②零点分区间法
③构造函数法
作业:P20第7题、第8题(1)(3)
练习:P20第8题(2)
补充练习:解不等式:
(1)1<|2x+1|≤3.
(2)||x-1|-4|<2.
(3)|3x-1|>x+3.
答案:(1){x|0
作业
8.解不等式:
