第四章因式分解复习 课件 2021-2022学年北师大版数学八年级下册(共22张PPT)
文档属性
| 名称 | 第四章因式分解复习 课件 2021-2022学年北师大版数学八年级下册(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 434.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 11:30:05 | ||
图片预览








文档简介
(共22张PPT)
因式分解
一、因式分解定义
把一个多项式化成几个整式乘积的形式,叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
关键三点
多项式
整式
乘积
1、下列各式由左边到右边的变形中,属于分解因式的是( ) A.a(x+y)=ax+ay B.x2﹣4x+4=x(x-4)+4C.10x2-5x=5x(2x-1) D.x2﹣16+6x=(x+4)(x-4)+6x
2.下列各式从左到右的变形,正确的是( )A.﹣x﹣y=﹣(x﹣y) B.﹣a+b=﹣(a+b) C.(y﹣x)2=(x﹣y)2 D.(a﹣b)3=(b﹣a)3
C
C
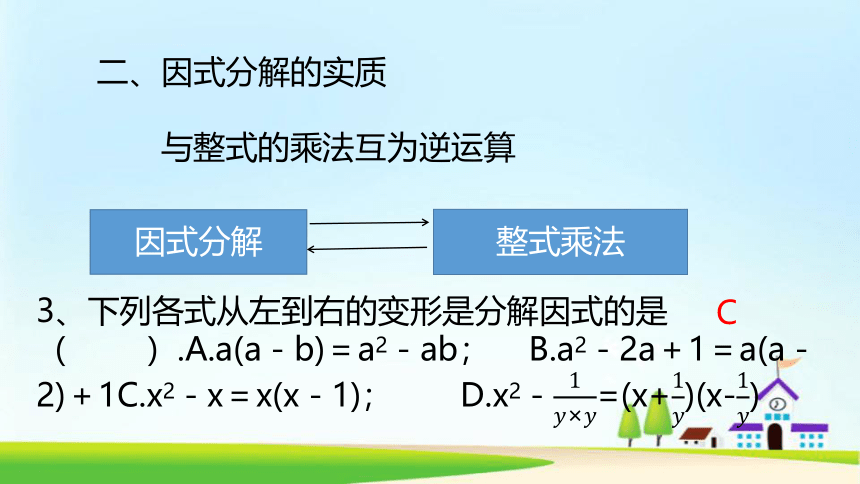
二、因式分解的实质
与整式的乘法互为逆运算
因式分解
整式乘法
3、下列各式从左到右的变形是分解因式的是( ).A.a(a-b)=a2-ab; B.a2-2a+1=a(a-2)+1C.x2-x=x(x-1); D.x2-=(x+)(x-)
C
4、下列各式从左到右的变形(1)15x2y=3x·5xy;(2)(x+y)(x-y)=x2-y2;(3)x2-6x+9=(x-3)2;(4)x2+4x+1=x(x+4+),其中是因式分解的个数是( )
A.1个 B.2个 C.3个 D.4个
5.下列各式因式分解正确的是 ( )A.a+b=b+aB.4x2y-8xy2+1=4xy(x-2y)+1C.a(a-b)=a2-abD.a2-2ab+2a=a(a-2b+2)
A
D
因式分解和分解因式的区别是什么?
答案:因式分解就是分解因式。
肉夹馍=馍夹肉?
肉夹馍≠么加肉
三、因式分解的方法
1.提公因式法
把多项式ma+mb+mc分解成两个因式的乘积的形式,其中一个因式是各项的公因式m,而另一个因式是(a+b+c),即ma+mab+mc=m(a+b+c),而(a+b+c)正好是ma+mb+mc除以m所得的商,提公因式法分解因式实际上是逆用乘法分配律.
6.多项式15m3n2+5m2n-20m2n3中各项的公因式是( )A.5mn B.5m2n2 C.5m2n D.5mn2
7.多项式﹣2a(x+y)3+6a2(x+y)的公因式是( ) A、﹣2a2(x+y)2 B、6a(x+y)
C、﹣2a(x+y) D、﹣2a
8.将-a2b-ab2提公因式后,另一个因式是( )A.a+2b B.-a+2b C.a+b D.a-2b
C
C
C
9.利用因式分解计算: ①(-3)201+(-3)200+6×3199;
解: 原式=+(-3)-6]
=(9-3-6)
=0
=0
9.利用因式分解计算: ②-2122-21222+21232.
解: 原式=-2122×(1+2122)+
=-2122×2123+
=2123×(-2122+2123)
=2123×1
=2123
10.下列各组式子中,没有公因式的一组是( )A.3(a+b)与6(a-b) B.2(a-b)与a-b C.(x+y)2与(x-y)2 D.3(a-b)3与2(b-a)2
11.将多项式a(b-2)-a2(2-b)因式分解的结果是( )A.(b-2)(a+a2) B.(b-2)(a-a2)
C.a(b-2)(a+1) D.a(b-2)(a-1)
12.(x+2)(2x-1)-(x+2)可以因式分解成(x+m)(2x+n),则m-n的值是( )A.2 B.-2 C.4 D.-4
C
B
C
13.因式分解: (1)(2x-3y)(a+b)+(3x-2y)(a+b);
解:原式=(a+b)[(2x-3y)+(3x-2y)]
=(a+b)(2x-3y+3x-2y)
=(a+b)(5x-5y)
=5(a+b)(x-y)
13.因式分解: (2)(m-n)4+m(m-n)3+n(n-m)3;
解:原式=(m-n)4+m(m-n)3-n(m-n)3
=[(m-n)+m-n]
=(2m-2n)
=2
13.因式分解: (3)x(x2-xy)-(4x2-4xy).
解: 原式=x(x2-xy)-4(x2-xy)
=(x2-xy)(x-4)
=x(x-y)(x-4)
14.已知x-2y=-5,xy=-2,则2x2y-4xy2=
解: 原式=2xy(x-2y)
∵x-2y=-5,xy=-2
∴原式=2×(-2)×(-5)
=20
20
2、公式法(1).平方差公式两个数的平方差等于这两个数的和与这两个数的差的积,即
(2).完全平方公式两个数的平方和加上这两个数的积的2倍,等于这两个数的和(差)的平方.即
-=(a+b)(a-b)
±2ab+=
要点诠释:
(1)平方差公式的特点:左边是两个数(整式)的平方,且符号相反,右边是两个数(整式)的和与这两个数(整式)的差的积.(2)完全平方公式的特点:左边是二次三项式,是这两数的平方和加(或减)这两数之积的2倍. 右边是两数的和(或差)的平方.(3)套用公式时要注意字母a,b,c的广泛意义,可以是字母,也可以是单项式或多项式.
15.下列四个多项式:①-a2+b2;②-x2-y2;③1-(a-1)2;④m2-2mn+n2,其中能用平方差公式分解因式的为( )A.①② B.①③ C.②④ D.②③
16.因式分解(2x+3)2-x2的结果是( )A.3(x2+4x+3) B.3(x2+2x+3) C.(3x+3)(x+3) D.3(x+1)(x+3)
17.已知多项式x2+a能用平方差公式在有理数范围内分解因式,那么在下列四个数中a可以等于( )A.9 B.4 C.-1 D.-2
B
C
D
18.把下列各式因式分解: (1)xn-xn+2;
解:原式=-(
=-(x+1)(x-1)
(2)-9x2+(x-y)2;
解:原式=-[-]
=-[3x+(x-y)][3x-(x-y)]
=-(3x+x-y)(3x-x+y)
=-(4x-y)(2x-y)
19.计算:2 0172×2-2 0162×2.
18.(3)a2(a-b)+b2(b-a).
解:原式=
=(a-b)()
=(a-b)(a+b)(a-b)
=(a+b)
解:原式=2×(
=2×(2017+2016)×(2017-2016)
=2×4033×1
=8066
因式分解步骤总结(1)如果多项式的各项有公因式,先提取公因式;(2)如果各项没有公因式那就尝试用公式法;(3)如用上述方法也不能分解,那么就得选择分组或其它方法来分解.(4)结果要彻底,即分解到不能再分解为止.
谢 谢
因式分解
一、因式分解定义
把一个多项式化成几个整式乘积的形式,叫做把这个多项式因式分解,也叫做把这个多项式分解因式。
关键三点
多项式
整式
乘积
1、下列各式由左边到右边的变形中,属于分解因式的是( ) A.a(x+y)=ax+ay B.x2﹣4x+4=x(x-4)+4C.10x2-5x=5x(2x-1) D.x2﹣16+6x=(x+4)(x-4)+6x
2.下列各式从左到右的变形,正确的是( )A.﹣x﹣y=﹣(x﹣y) B.﹣a+b=﹣(a+b) C.(y﹣x)2=(x﹣y)2 D.(a﹣b)3=(b﹣a)3
C
C
二、因式分解的实质
与整式的乘法互为逆运算
因式分解
整式乘法
3、下列各式从左到右的变形是分解因式的是( ).A.a(a-b)=a2-ab; B.a2-2a+1=a(a-2)+1C.x2-x=x(x-1); D.x2-=(x+)(x-)
C
4、下列各式从左到右的变形(1)15x2y=3x·5xy;(2)(x+y)(x-y)=x2-y2;(3)x2-6x+9=(x-3)2;(4)x2+4x+1=x(x+4+),其中是因式分解的个数是( )
A.1个 B.2个 C.3个 D.4个
5.下列各式因式分解正确的是 ( )A.a+b=b+aB.4x2y-8xy2+1=4xy(x-2y)+1C.a(a-b)=a2-abD.a2-2ab+2a=a(a-2b+2)
A
D
因式分解和分解因式的区别是什么?
答案:因式分解就是分解因式。
肉夹馍=馍夹肉?
肉夹馍≠么加肉
三、因式分解的方法
1.提公因式法
把多项式ma+mb+mc分解成两个因式的乘积的形式,其中一个因式是各项的公因式m,而另一个因式是(a+b+c),即ma+mab+mc=m(a+b+c),而(a+b+c)正好是ma+mb+mc除以m所得的商,提公因式法分解因式实际上是逆用乘法分配律.
6.多项式15m3n2+5m2n-20m2n3中各项的公因式是( )A.5mn B.5m2n2 C.5m2n D.5mn2
7.多项式﹣2a(x+y)3+6a2(x+y)的公因式是( ) A、﹣2a2(x+y)2 B、6a(x+y)
C、﹣2a(x+y) D、﹣2a
8.将-a2b-ab2提公因式后,另一个因式是( )A.a+2b B.-a+2b C.a+b D.a-2b
C
C
C
9.利用因式分解计算: ①(-3)201+(-3)200+6×3199;
解: 原式=+(-3)-6]
=(9-3-6)
=0
=0
9.利用因式分解计算: ②-2122-21222+21232.
解: 原式=-2122×(1+2122)+
=-2122×2123+
=2123×(-2122+2123)
=2123×1
=2123
10.下列各组式子中,没有公因式的一组是( )A.3(a+b)与6(a-b) B.2(a-b)与a-b C.(x+y)2与(x-y)2 D.3(a-b)3与2(b-a)2
11.将多项式a(b-2)-a2(2-b)因式分解的结果是( )A.(b-2)(a+a2) B.(b-2)(a-a2)
C.a(b-2)(a+1) D.a(b-2)(a-1)
12.(x+2)(2x-1)-(x+2)可以因式分解成(x+m)(2x+n),则m-n的值是( )A.2 B.-2 C.4 D.-4
C
B
C
13.因式分解: (1)(2x-3y)(a+b)+(3x-2y)(a+b);
解:原式=(a+b)[(2x-3y)+(3x-2y)]
=(a+b)(2x-3y+3x-2y)
=(a+b)(5x-5y)
=5(a+b)(x-y)
13.因式分解: (2)(m-n)4+m(m-n)3+n(n-m)3;
解:原式=(m-n)4+m(m-n)3-n(m-n)3
=[(m-n)+m-n]
=(2m-2n)
=2
13.因式分解: (3)x(x2-xy)-(4x2-4xy).
解: 原式=x(x2-xy)-4(x2-xy)
=(x2-xy)(x-4)
=x(x-y)(x-4)
14.已知x-2y=-5,xy=-2,则2x2y-4xy2=
解: 原式=2xy(x-2y)
∵x-2y=-5,xy=-2
∴原式=2×(-2)×(-5)
=20
20
2、公式法(1).平方差公式两个数的平方差等于这两个数的和与这两个数的差的积,即
(2).完全平方公式两个数的平方和加上这两个数的积的2倍,等于这两个数的和(差)的平方.即
-=(a+b)(a-b)
±2ab+=
要点诠释:
(1)平方差公式的特点:左边是两个数(整式)的平方,且符号相反,右边是两个数(整式)的和与这两个数(整式)的差的积.(2)完全平方公式的特点:左边是二次三项式,是这两数的平方和加(或减)这两数之积的2倍. 右边是两数的和(或差)的平方.(3)套用公式时要注意字母a,b,c的广泛意义,可以是字母,也可以是单项式或多项式.
15.下列四个多项式:①-a2+b2;②-x2-y2;③1-(a-1)2;④m2-2mn+n2,其中能用平方差公式分解因式的为( )A.①② B.①③ C.②④ D.②③
16.因式分解(2x+3)2-x2的结果是( )A.3(x2+4x+3) B.3(x2+2x+3) C.(3x+3)(x+3) D.3(x+1)(x+3)
17.已知多项式x2+a能用平方差公式在有理数范围内分解因式,那么在下列四个数中a可以等于( )A.9 B.4 C.-1 D.-2
B
C
D
18.把下列各式因式分解: (1)xn-xn+2;
解:原式=-(
=-(x+1)(x-1)
(2)-9x2+(x-y)2;
解:原式=-[-]
=-[3x+(x-y)][3x-(x-y)]
=-(3x+x-y)(3x-x+y)
=-(4x-y)(2x-y)
19.计算:2 0172×2-2 0162×2.
18.(3)a2(a-b)+b2(b-a).
解:原式=
=(a-b)()
=(a-b)(a+b)(a-b)
=(a+b)
解:原式=2×(
=2×(2017+2016)×(2017-2016)
=2×4033×1
=8066
因式分解步骤总结(1)如果多项式的各项有公因式,先提取公因式;(2)如果各项没有公因式那就尝试用公式法;(3)如用上述方法也不能分解,那么就得选择分组或其它方法来分解.(4)结果要彻底,即分解到不能再分解为止.
谢 谢
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
