鲁教版(五四制)数学七年级上册 第一章 三角形 复习课件(37张)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 第一章 三角形 复习课件(37张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 11:02:58 | ||
图片预览









文档简介
(共37张PPT)
第一章 三角形
复习课件
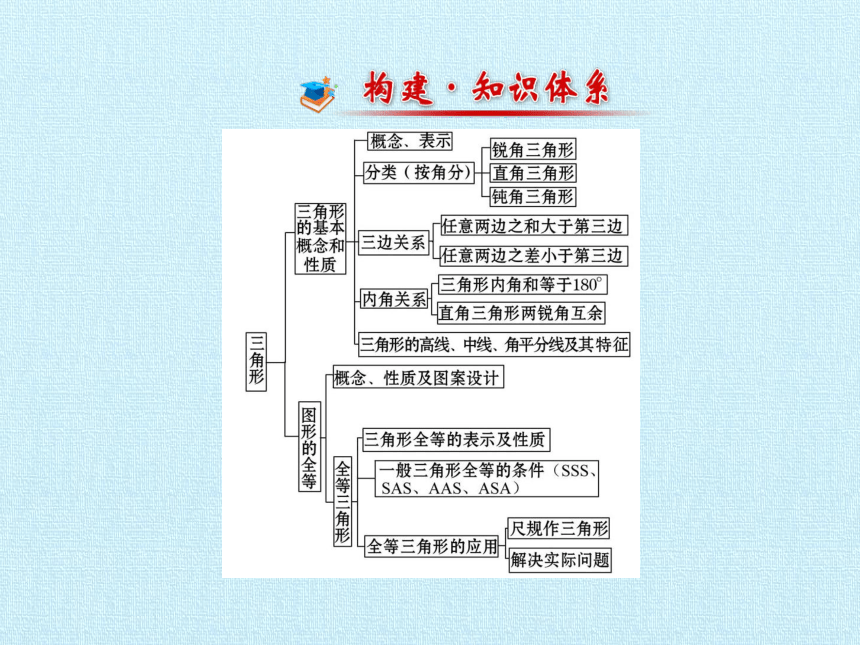
一、三角形的相关概念
1.三角形的概念:
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.三条线段叫做三角形的边,公共的端点叫做三角形的顶点,两边所形成的夹角叫做三角形的内角.三角形用符号“△”及顶点字母表示.
2.与三角形有关的线段:
三角形的高线、中线、角平分线:
(1)三线都经过顶点.
(2)都是线段.
(3)除直角三角形的两条高线在三角形的两条直角边上,钝角三角形的两条高线在三角形外部,其他各线均在三角形内.
(4)锐角三角形的高交于三角形内部一点,直角三角形的高交于三角形的直角顶点,钝角三角形的高所在的直线交于三角形外部一点.
(5)三角形的一条中线把三角形分成两个面积相等的小三角形.
(6)根据面积法可得,三角形的各边与这边上的高的乘积相等.
3.三角形的分类:
(1)按角分类:锐角三角形、直角三角形、钝角三角形.
(2)按边分类:
4.全等三角形的概念:
能够完全重合的两个三角形叫做全等三角形.
二、三角形的相关性质和判定
1.三角形的性质:
(1)三角形的稳定性:三角形的三边确定了,那么它的形状大小就都确定了,三角形的这个性质叫做三角形的稳定性.
(2)三角形三边之间的性质:三角形任意两边之和大于第三边,任意两边之差小于第三边.
2.三角形内角和性质:
三角形三个内角的和等于180°.
3.全等三角形:
(1)全等三角形的性质:
全等三角形的对应边相等,对应角相等,对应边上的中线、高线,对应角的角平分线分别相等;全等三角形的周长、面积分别相等.
全等三角形的性质是判定线段、角相等的重要依据.
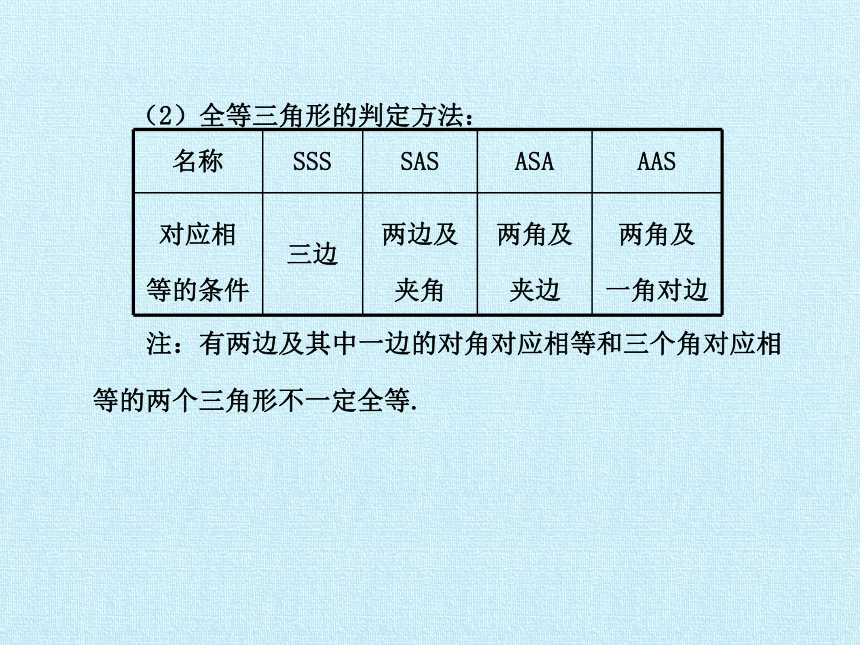
(2)全等三角形的判定方法:
注:有两边及其中一边的对角对应相等和三个角对应相等的两个三角形不一定全等.
名称 SSS SAS ASA AAS
对应相 等的条件 三边 两边及 夹角 两角及 夹边 两角及
一角对边
(3)判定两个三角形全等时要认真分析条件和图形结构,理清已知与未知之间的内在联系,从而选择恰当的方法.
(4)以后将会学到的平移、旋转、翻折都是全等变换.在学习的过程中,对两个三角形进行不同的组合变换,拼成不同的图形,在复杂的图形当中,学会对图形进行分离、整合,准确找出全等三角形的对应元素.
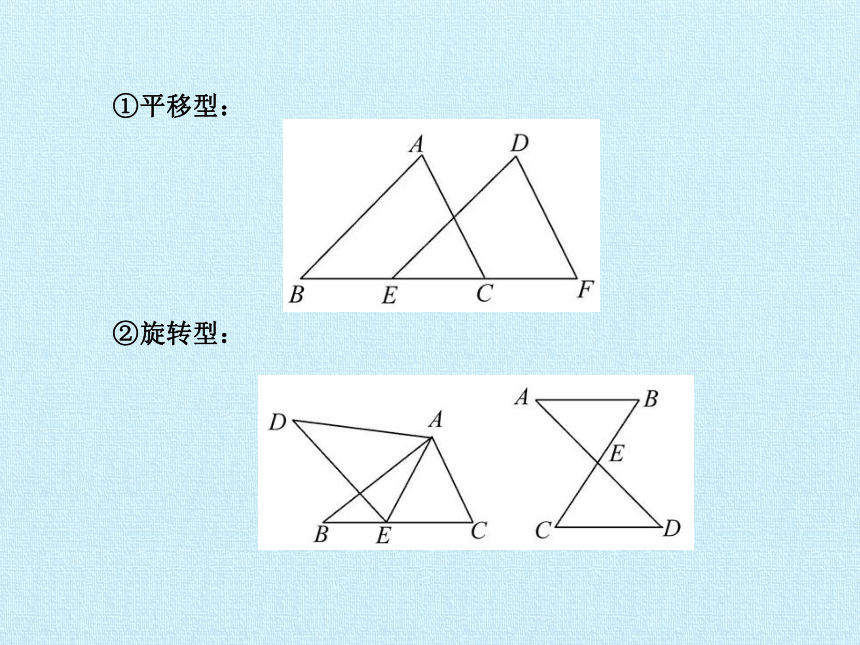
理解并熟记全等三角形中经常出现的图形结构,充分挖掘其中的隐含条件,如图.
①平移型:
②旋转型:
③翻折型:
④组合型:
三、全等三角形的应用
1.全等三角形的应用主要体现在判定线段或角的相等问题中,在实际问题中,往往构造全等三角形,再利用全等三角形的性质解决测量(不能直接度量长度)问题、三角形物体复原问题等.
2.涉及实际问题中的测量方案设计问题时,要考虑测量工具及条件的局限性,叙述测量方案时要严谨、有条理.
热点考向1三角形的边角关系
【相关链接】
三角形的性质分为边的性质与内角的性质
(1)三边关系:任意两边之和大于第三边,任意两边之差小于第三边.
(2)内角关系:三角形内角的和是180°.
【例1】(2012·海南中考)一个三角形的两边长分别为3cm和7cm,则此三角形的第三边的长可能是( )
(A)3cm (B)4cm (C)7cm (D)11cm
【思路点拨】 → →
【自主解答】选C.设第三边长为xcm,则由三角形三边关系定理得7-3<x<7+3,即4<x<10.因此,本题的第三边应满足4<x<10,把各项代入不等式符合的即为答案.3,4,11都不符合不等式4<x<10,只有7符合,故选C.
三边关系
第三边取值范围
代入得出答案
热点考向2全等三角形的判别
【相关链接】
三角形全等的四种判定方法:SSS、SAS、ASA、AAS,说明三角形全等的三类条件:直接条件、隐含条件、间接条件.
【例2】(2012·广元中考)如图,在△AEC
和△DFB中,∠E=∠F,点A,B,C,D在同
一条直线上,有如下三个关系式:①AE∥DF;
②AB=CD;③CE=BF.
(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有题目(用序号写出题目书写格式:“如果?,?,那么?”)
(2)选择(1)中你写出的一个题目,说明它正确的理由.
【思路点拨】
→ →
→
→
从三个条件中选两个条件共有三种方法
即选取①②,①③和②③
结合三角形全等的判定方法判断是否正确
写出正确的题目
用相应方法说明理由
【自主解答】(1)题目1:如果①,②,那么③;
题目2:如果①,③,那么②.
(2)题目1:
因为①AE∥DF,所以∠A=∠D,
因为②AB=CD,
所以AB+BC=CD+BC,即AC=DB.
在△AEC和△DFB中,
因为∠E=∠F,∠A=∠D,AC=DB,
所以△AEC≌△DFB(AAS),
所以CE=BF③(全等三角形对应边相等)
题目2:
因为①AE∥DF,所以∠A=∠D.
在△AEC和△DFB中,
因为∠E=∠F,∠A=∠D,③CE=BF,
所以△AEC≌△DFB(AAS),
所以AC=DB(全等三角形对应边相等),
则AC-BC=DB-BC,即AB=CD②.
注:题目“如果②,③,那么①”是错误的.
热点考向3全等三角形的应用
【相关链接】
全等三角形是说明线段或角相等的重要方法之一,用全等三角形解题的关键是确定或构造两个三角形全等,全等三角形的周长和面积相等也是中考考查的内容.
【例3】(2012·哈尔滨中考)如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.试说明AC=AD.
【教你解题】
【命题揭秘】
三角形在中考中是重要考查点之一,对于三角形的性质和相关概念,只进行一般性考查,题目比较简单,题型多为选择题或填空题;三角形全等及其应用是中考的命题热点,重点考查全等三角形的判定,命题方式比较广泛,在解答题目中更为常见.
1.(2012·恩施中考)如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于
( )
(A)50° (B)60° (C)65° (D)90°
【解析】选C.方法一:因为AB∥CD,所以∠FEB+∠1=180°,
∠2=∠GEB(两直线平行,同旁内角互补,内错角相等).因为
∠1=50°,所以∠FEB=180°-50°=130°.因为EG平分∠FEB,
所以∠GEB= ×130°=65°,所以∠2=65°.
方法二:因为AB∥CD,所以∠FEB+∠1=180°,∠2=∠GEB
(两直线平行,同旁内角互补).因为∠1=50°,
所以∠FEB=180°-50°=130°.因为EG平分∠FEB,
所以∠GEF= ×130°=65°,
所以∠2=180°-50°-65°=65°.
2.(2012·河源中考)如图,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=( )
(A)150° (B)210° (C)105° (D)75°
【解析】选A.由折叠知∠A′=∠A=75°,
因为∠A+∠AED+∠ADE
=∠A′+∠A′ED+∠A′DE=180°,
所以∠A+∠AED+∠ADE+∠A′+∠A′ED+∠A′DE=360°,
因为∠1+∠AED+∠A′ED=∠2+∠ADE+∠A′DE=180°,
所以∠1+∠AED+∠A′ED+∠2+∠ADE+∠A′DE=360°,
所以∠1+∠2=∠A+∠A′=2∠A=150°,故选A.
3.(2012·聊城中考)将一副三角板按如图所示摆放,图中∠a的度数是( )
(A)75° (B)90° (C)105° (D)120°
【解析】选C.∠a的度数为180°-45°-30°=105°.
4.(2012·云南中考)如图,在△ABC中,
∠B=67°,∠C=33°,AD是△ABC的角
平分线,则∠CAD的度数为( )
(A)40° (B)45° (C)50° (D)55°
【解析】选A.因为∠B=67°,∠C=33°,
所以∠BAC=80°,
因为AD是△ABC的角平分线,
所以∠CAD= ∠BAC=40°.
5.(2012·泰州中考)如图,在△ABC中,
∠C=90°,∠BAC的平分线交BC于点D,
若CD=4,则点D到AB的距离是_______.
【解析】过点D作DE⊥AB,垂足为E,因为∠C=90°,所以∠ACD=∠AED,又AD平分∠BAC,所以∠CAD=∠EAD,又AD=AD,所以△ACD≌△AED(AAS),所以DE=CD=4,即点D到AB的距离为4.
答案:4
6.(2012·眉山中考)在△ABC中,AB=5,AC=3,AD是BC边上的中线,则AD的取值范围是_________.
【解析】如图,延长AD至点E,使DE=AD,
连接CE.因为AD是BC边上的中线,所以
BD=CD.在△ABD和△ECD中,
所以△ABD≌△ECD(SAS),
所以EC=AB=5,
在△ACE中,EC-AC即5-3<2AD<3+5,
所以1答案:17.(2012·广州中考)如图,点D在AB上,
点E在AC上,AB=AC,∠B=∠C.试说明BE=CD.
【解析】在△ABE和△ACD中,
所以△ABE≌△ACD,
所以BE=CD.
8.如图,在四边形ABCD中,AD∥BC,
E为CD的中点,连接AE,BE,BE⊥AE,
延长AE交BC的延长线于点F.
试说明:(1)FC=AD.
(2)AB=BC+AD.
【解析】(1)因为E是CD的中点,
所以DE=CE.因为AD∥BC,
所以∠ADE=∠FCE,∠DAE=∠CFE.
所以△ADE≌△FCE(AAS).
所以FC=AD.
(2)因为△ADE≌△FCE,所以AE=FE.
又因为BE⊥AE,
所以∠BEA=∠BEF=90°,
又因为BE=BE,
所以△BEA≌△BEF(SAS).所以AB=FB.
因为FB=BC+FC=BC+AD.
所以AB=BC+AD.
9.(2012·漳州中考)在数学课上,林老师在黑板上画出如图所示的图形(其中B,F,C,E在同一直线上),并写出四个条件:
①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.
请你从这四个条件中选出三个作为条件,另一个作为结论组成一个正确的题目,并给出理由.
题设:_________;结论:_________.(均填写序号)
理由:
【解析】答案不惟一,如①③④②
理由:因为∠1=∠2,∠B=∠E,AB=DE,
所以△ABC≌△DEF,
所以BC=EF.
因为BC=BF+CF,EF=CE+CF,
所以BF=CE.
此题也可以把①②③作条件,④作结论;
或者把②③④作条件,①作结论.
谢 谢
第一章 三角形
复习课件
一、三角形的相关概念
1.三角形的概念:
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.三条线段叫做三角形的边,公共的端点叫做三角形的顶点,两边所形成的夹角叫做三角形的内角.三角形用符号“△”及顶点字母表示.
2.与三角形有关的线段:
三角形的高线、中线、角平分线:
(1)三线都经过顶点.
(2)都是线段.
(3)除直角三角形的两条高线在三角形的两条直角边上,钝角三角形的两条高线在三角形外部,其他各线均在三角形内.
(4)锐角三角形的高交于三角形内部一点,直角三角形的高交于三角形的直角顶点,钝角三角形的高所在的直线交于三角形外部一点.
(5)三角形的一条中线把三角形分成两个面积相等的小三角形.
(6)根据面积法可得,三角形的各边与这边上的高的乘积相等.
3.三角形的分类:
(1)按角分类:锐角三角形、直角三角形、钝角三角形.
(2)按边分类:
4.全等三角形的概念:
能够完全重合的两个三角形叫做全等三角形.
二、三角形的相关性质和判定
1.三角形的性质:
(1)三角形的稳定性:三角形的三边确定了,那么它的形状大小就都确定了,三角形的这个性质叫做三角形的稳定性.
(2)三角形三边之间的性质:三角形任意两边之和大于第三边,任意两边之差小于第三边.
2.三角形内角和性质:
三角形三个内角的和等于180°.
3.全等三角形:
(1)全等三角形的性质:
全等三角形的对应边相等,对应角相等,对应边上的中线、高线,对应角的角平分线分别相等;全等三角形的周长、面积分别相等.
全等三角形的性质是判定线段、角相等的重要依据.
(2)全等三角形的判定方法:
注:有两边及其中一边的对角对应相等和三个角对应相等的两个三角形不一定全等.
名称 SSS SAS ASA AAS
对应相 等的条件 三边 两边及 夹角 两角及 夹边 两角及
一角对边
(3)判定两个三角形全等时要认真分析条件和图形结构,理清已知与未知之间的内在联系,从而选择恰当的方法.
(4)以后将会学到的平移、旋转、翻折都是全等变换.在学习的过程中,对两个三角形进行不同的组合变换,拼成不同的图形,在复杂的图形当中,学会对图形进行分离、整合,准确找出全等三角形的对应元素.
理解并熟记全等三角形中经常出现的图形结构,充分挖掘其中的隐含条件,如图.
①平移型:
②旋转型:
③翻折型:
④组合型:
三、全等三角形的应用
1.全等三角形的应用主要体现在判定线段或角的相等问题中,在实际问题中,往往构造全等三角形,再利用全等三角形的性质解决测量(不能直接度量长度)问题、三角形物体复原问题等.
2.涉及实际问题中的测量方案设计问题时,要考虑测量工具及条件的局限性,叙述测量方案时要严谨、有条理.
热点考向1三角形的边角关系
【相关链接】
三角形的性质分为边的性质与内角的性质
(1)三边关系:任意两边之和大于第三边,任意两边之差小于第三边.
(2)内角关系:三角形内角的和是180°.
【例1】(2012·海南中考)一个三角形的两边长分别为3cm和7cm,则此三角形的第三边的长可能是( )
(A)3cm (B)4cm (C)7cm (D)11cm
【思路点拨】 → →
【自主解答】选C.设第三边长为xcm,则由三角形三边关系定理得7-3<x<7+3,即4<x<10.因此,本题的第三边应满足4<x<10,把各项代入不等式符合的即为答案.3,4,11都不符合不等式4<x<10,只有7符合,故选C.
三边关系
第三边取值范围
代入得出答案
热点考向2全等三角形的判别
【相关链接】
三角形全等的四种判定方法:SSS、SAS、ASA、AAS,说明三角形全等的三类条件:直接条件、隐含条件、间接条件.
【例2】(2012·广元中考)如图,在△AEC
和△DFB中,∠E=∠F,点A,B,C,D在同
一条直线上,有如下三个关系式:①AE∥DF;
②AB=CD;③CE=BF.
(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有题目(用序号写出题目书写格式:“如果?,?,那么?”)
(2)选择(1)中你写出的一个题目,说明它正确的理由.
【思路点拨】
→ →
→
→
从三个条件中选两个条件共有三种方法
即选取①②,①③和②③
结合三角形全等的判定方法判断是否正确
写出正确的题目
用相应方法说明理由
【自主解答】(1)题目1:如果①,②,那么③;
题目2:如果①,③,那么②.
(2)题目1:
因为①AE∥DF,所以∠A=∠D,
因为②AB=CD,
所以AB+BC=CD+BC,即AC=DB.
在△AEC和△DFB中,
因为∠E=∠F,∠A=∠D,AC=DB,
所以△AEC≌△DFB(AAS),
所以CE=BF③(全等三角形对应边相等)
题目2:
因为①AE∥DF,所以∠A=∠D.
在△AEC和△DFB中,
因为∠E=∠F,∠A=∠D,③CE=BF,
所以△AEC≌△DFB(AAS),
所以AC=DB(全等三角形对应边相等),
则AC-BC=DB-BC,即AB=CD②.
注:题目“如果②,③,那么①”是错误的.
热点考向3全等三角形的应用
【相关链接】
全等三角形是说明线段或角相等的重要方法之一,用全等三角形解题的关键是确定或构造两个三角形全等,全等三角形的周长和面积相等也是中考考查的内容.
【例3】(2012·哈尔滨中考)如图,点B在射线AE上,∠CAE=∠DAE,∠CBE=∠DBE.试说明AC=AD.
【教你解题】
【命题揭秘】
三角形在中考中是重要考查点之一,对于三角形的性质和相关概念,只进行一般性考查,题目比较简单,题型多为选择题或填空题;三角形全等及其应用是中考的命题热点,重点考查全等三角形的判定,命题方式比较广泛,在解答题目中更为常见.
1.(2012·恩施中考)如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于
( )
(A)50° (B)60° (C)65° (D)90°
【解析】选C.方法一:因为AB∥CD,所以∠FEB+∠1=180°,
∠2=∠GEB(两直线平行,同旁内角互补,内错角相等).因为
∠1=50°,所以∠FEB=180°-50°=130°.因为EG平分∠FEB,
所以∠GEB= ×130°=65°,所以∠2=65°.
方法二:因为AB∥CD,所以∠FEB+∠1=180°,∠2=∠GEB
(两直线平行,同旁内角互补).因为∠1=50°,
所以∠FEB=180°-50°=130°.因为EG平分∠FEB,
所以∠GEF= ×130°=65°,
所以∠2=180°-50°-65°=65°.
2.(2012·河源中考)如图,在折纸活动中,小明制作了一张△ABC纸片,点D,E分别在边AB,AC上,将△ABC沿着DE折叠压平,A与A′重合,若∠A=75°,则∠1+∠2=( )
(A)150° (B)210° (C)105° (D)75°
【解析】选A.由折叠知∠A′=∠A=75°,
因为∠A+∠AED+∠ADE
=∠A′+∠A′ED+∠A′DE=180°,
所以∠A+∠AED+∠ADE+∠A′+∠A′ED+∠A′DE=360°,
因为∠1+∠AED+∠A′ED=∠2+∠ADE+∠A′DE=180°,
所以∠1+∠AED+∠A′ED+∠2+∠ADE+∠A′DE=360°,
所以∠1+∠2=∠A+∠A′=2∠A=150°,故选A.
3.(2012·聊城中考)将一副三角板按如图所示摆放,图中∠a的度数是( )
(A)75° (B)90° (C)105° (D)120°
【解析】选C.∠a的度数为180°-45°-30°=105°.
4.(2012·云南中考)如图,在△ABC中,
∠B=67°,∠C=33°,AD是△ABC的角
平分线,则∠CAD的度数为( )
(A)40° (B)45° (C)50° (D)55°
【解析】选A.因为∠B=67°,∠C=33°,
所以∠BAC=80°,
因为AD是△ABC的角平分线,
所以∠CAD= ∠BAC=40°.
5.(2012·泰州中考)如图,在△ABC中,
∠C=90°,∠BAC的平分线交BC于点D,
若CD=4,则点D到AB的距离是_______.
【解析】过点D作DE⊥AB,垂足为E,因为∠C=90°,所以∠ACD=∠AED,又AD平分∠BAC,所以∠CAD=∠EAD,又AD=AD,所以△ACD≌△AED(AAS),所以DE=CD=4,即点D到AB的距离为4.
答案:4
6.(2012·眉山中考)在△ABC中,AB=5,AC=3,AD是BC边上的中线,则AD的取值范围是_________.
【解析】如图,延长AD至点E,使DE=AD,
连接CE.因为AD是BC边上的中线,所以
BD=CD.在△ABD和△ECD中,
所以△ABD≌△ECD(SAS),
所以EC=AB=5,
在△ACE中,EC-AC
所以1
点E在AC上,AB=AC,∠B=∠C.试说明BE=CD.
【解析】在△ABE和△ACD中,
所以△ABE≌△ACD,
所以BE=CD.
8.如图,在四边形ABCD中,AD∥BC,
E为CD的中点,连接AE,BE,BE⊥AE,
延长AE交BC的延长线于点F.
试说明:(1)FC=AD.
(2)AB=BC+AD.
【解析】(1)因为E是CD的中点,
所以DE=CE.因为AD∥BC,
所以∠ADE=∠FCE,∠DAE=∠CFE.
所以△ADE≌△FCE(AAS).
所以FC=AD.
(2)因为△ADE≌△FCE,所以AE=FE.
又因为BE⊥AE,
所以∠BEA=∠BEF=90°,
又因为BE=BE,
所以△BEA≌△BEF(SAS).所以AB=FB.
因为FB=BC+FC=BC+AD.
所以AB=BC+AD.
9.(2012·漳州中考)在数学课上,林老师在黑板上画出如图所示的图形(其中B,F,C,E在同一直线上),并写出四个条件:
①AB=DE,②BF=EC,③∠B=∠E,④∠1=∠2.
请你从这四个条件中选出三个作为条件,另一个作为结论组成一个正确的题目,并给出理由.
题设:_________;结论:_________.(均填写序号)
理由:
【解析】答案不惟一,如①③④②
理由:因为∠1=∠2,∠B=∠E,AB=DE,
所以△ABC≌△DEF,
所以BC=EF.
因为BC=BF+CF,EF=CE+CF,
所以BF=CE.
此题也可以把①②③作条件,④作结论;
或者把②③④作条件,①作结论.
谢 谢
