24.1.3 弧、弦、圆心角 人教版九年级数学上册课时作业(含答案)
文档属性
| 名称 | 24.1.3 弧、弦、圆心角 人教版九年级数学上册课时作业(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 324.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 12:26:04 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级数学上册课时作业
第二十四章 圆
24.1.3 弧、弦、圆心角
1. 下列语句中,不正确的是( )
A.圆是中心对称图形
B.圆是轴对称图形,过圆心的直线是它的对称轴
C.当圆绕它的中心旋转89°57'时,不会与原来的圆重合
D.圆的对称轴有无数条,但是对称中心只有一个
2. 下列图中,∠AOB是圆心角的是( )
A B C D
3. 如图所示,在☉O中,AB,CD是两条弦,OM⊥CD,ON⊥AB,如果AB=CD,则下列结论不正确的是( )
A.∠AON=∠DOM B.AN=DM C.OM=DM D.OM=ON
4. 如图,在☉O中,如果∠AOB=2∠COD,那么( )
A.AB=DC B.AB2DC D.AB<2DC
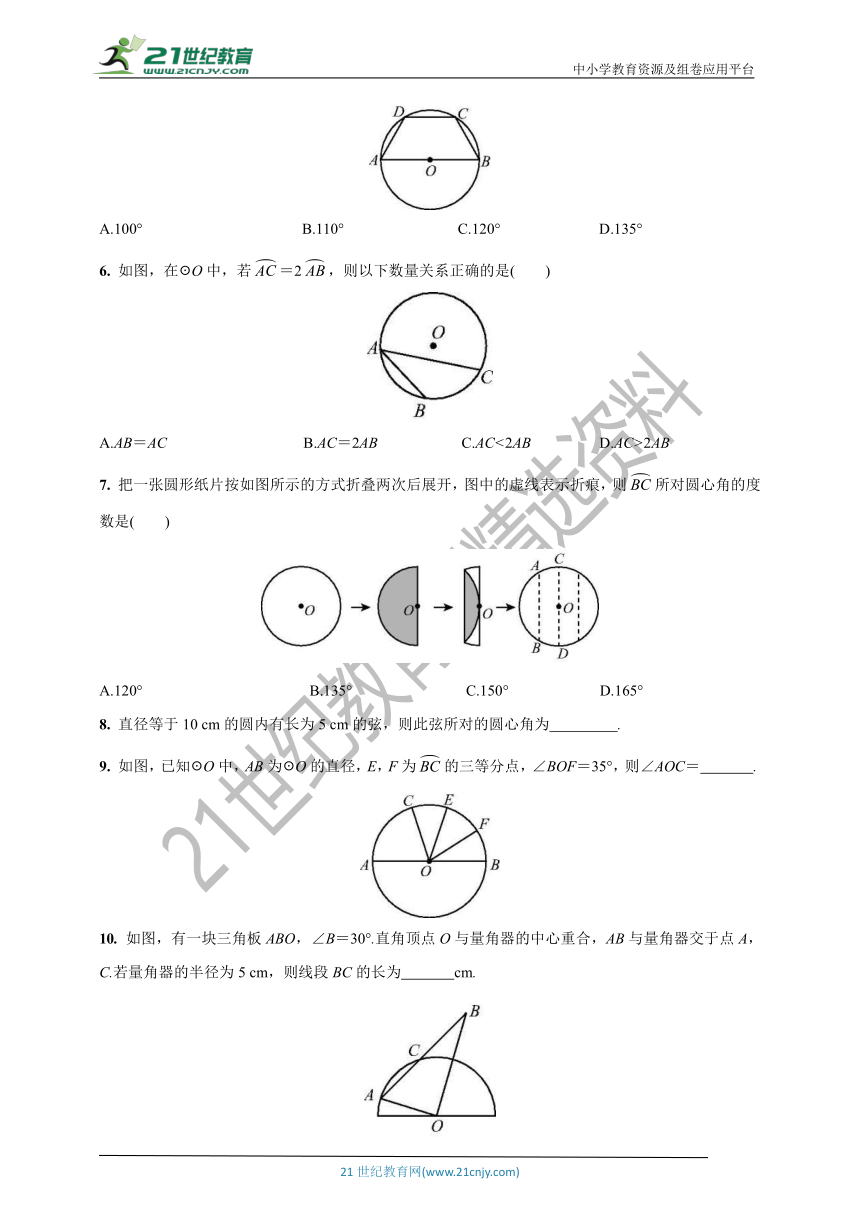
5. 如图,AB是☉O的直径,BC,CD,DA是☉O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.135°
6. 如图,在☉O中,若=2,则以下数量关系正确的是( )
A.AB=AC B.AC=2AB C.AC<2AB D.AC>2AB
7. 把一张圆形纸片按如图所示的方式折叠两次后展开,图中的虚线表示折痕,则所对圆心角的度数是( )
A.120° B.135° C.150° D.165°
8. 直径等于10 cm的圆内有长为5 cm的弦,则此弦所对的圆心角为 .
9. 如图,已知☉O中,AB为☉O的直径,E,F为的三等分点,∠BOF=35°,则∠AOC= .
10. 如图,有一块三角板ABO,∠B=30°.直角顶点O与量角器的中心重合,AB与量角器交于点A,C.若量角器的半径为5 cm,则线段BC的长为 cm.
11. 如图,C为的中点,CN⊥OB于点N,CD⊥OA于点M,CD=4 cm,则CN= cm.
12. 如图,在☉O中,AC=BD,∠1=30°,求∠2的度数.
13. 如图,已知AB是☉O的直径,弦AC∥OD.
(1)求证:=;
(2)若所对圆心角的度数为58°,求∠AOD的度数.
14. 如图1,PC是☉O的直径,PA与PB是弦,且∠APC=∠BPC.
(1)求证:PA=PB.
(2)如果点P由圆上运动到圆外,PC过圆心.如图2,是否仍有PA=PB 为什么
(3)如果点P由圆上运动到圆内,PC过圆心,如图3,是否仍有PA=PB (直接写出结论,不必说明理由)
参 考 答 案
1. C 2. C 3. C 4. D 5. C 6. C 7. C
8. 60° 9. 75° 10. 5 11. 2
12. 解:∵在☉O中,AC=BD,∴∠AOC=∠BOD,∴∠1+∠BOC=∠2+∠BOC,∴∠1=∠2=30°.
13. 解:(1)连接OC.∵OA=OC,∴∠OAC=∠ACO. ∵AC∥OD,∴∠OAC=∠BOD,∠COD=∠ACO. ∴∠BOD=∠COD,∴=.
(2)∵=,∠AOC=58°,∴∠BOD=∠COD=∠BOC=(180°-58°)=61°,∴∠AOD=∠AOC+∠COD=119°.
14. 解:(1)作OE⊥PA于点E,OF⊥PB于点F,∴∠OEP=∠OFP=90°. 在△POE和△POF中, ∴△POE≌△POF,∴PE=PF. 又∵PE=PA,PF=PB,∴PA=PB.
(2)作OE⊥PA于点E,OF⊥PB于点F,∴∠OEP=∠OFP=90°. 在△POE和△POF中, ∴△POE≌△POF,∴OE=OF,PE=PF,∴AE=BF,∴PA=PB.
(3)仍有PA=PB.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学上册课时作业
第二十四章 圆
24.1.3 弧、弦、圆心角
1. 下列语句中,不正确的是( )
A.圆是中心对称图形
B.圆是轴对称图形,过圆心的直线是它的对称轴
C.当圆绕它的中心旋转89°57'时,不会与原来的圆重合
D.圆的对称轴有无数条,但是对称中心只有一个
2. 下列图中,∠AOB是圆心角的是( )
A B C D
3. 如图所示,在☉O中,AB,CD是两条弦,OM⊥CD,ON⊥AB,如果AB=CD,则下列结论不正确的是( )
A.∠AON=∠DOM B.AN=DM C.OM=DM D.OM=ON
4. 如图,在☉O中,如果∠AOB=2∠COD,那么( )
A.AB=DC B.AB
5. 如图,AB是☉O的直径,BC,CD,DA是☉O的弦,且BC=CD=DA,则∠BCD等于( )
A.100° B.110° C.120° D.135°
6. 如图,在☉O中,若=2,则以下数量关系正确的是( )
A.AB=AC B.AC=2AB C.AC<2AB D.AC>2AB
7. 把一张圆形纸片按如图所示的方式折叠两次后展开,图中的虚线表示折痕,则所对圆心角的度数是( )
A.120° B.135° C.150° D.165°
8. 直径等于10 cm的圆内有长为5 cm的弦,则此弦所对的圆心角为 .
9. 如图,已知☉O中,AB为☉O的直径,E,F为的三等分点,∠BOF=35°,则∠AOC= .
10. 如图,有一块三角板ABO,∠B=30°.直角顶点O与量角器的中心重合,AB与量角器交于点A,C.若量角器的半径为5 cm,则线段BC的长为 cm.
11. 如图,C为的中点,CN⊥OB于点N,CD⊥OA于点M,CD=4 cm,则CN= cm.
12. 如图,在☉O中,AC=BD,∠1=30°,求∠2的度数.
13. 如图,已知AB是☉O的直径,弦AC∥OD.
(1)求证:=;
(2)若所对圆心角的度数为58°,求∠AOD的度数.
14. 如图1,PC是☉O的直径,PA与PB是弦,且∠APC=∠BPC.
(1)求证:PA=PB.
(2)如果点P由圆上运动到圆外,PC过圆心.如图2,是否仍有PA=PB 为什么
(3)如果点P由圆上运动到圆内,PC过圆心,如图3,是否仍有PA=PB (直接写出结论,不必说明理由)
参 考 答 案
1. C 2. C 3. C 4. D 5. C 6. C 7. C
8. 60° 9. 75° 10. 5 11. 2
12. 解:∵在☉O中,AC=BD,∴∠AOC=∠BOD,∴∠1+∠BOC=∠2+∠BOC,∴∠1=∠2=30°.
13. 解:(1)连接OC.∵OA=OC,∴∠OAC=∠ACO. ∵AC∥OD,∴∠OAC=∠BOD,∠COD=∠ACO. ∴∠BOD=∠COD,∴=.
(2)∵=,∠AOC=58°,∴∠BOD=∠COD=∠BOC=(180°-58°)=61°,∴∠AOD=∠AOC+∠COD=119°.
14. 解:(1)作OE⊥PA于点E,OF⊥PB于点F,∴∠OEP=∠OFP=90°. 在△POE和△POF中, ∴△POE≌△POF,∴PE=PF. 又∵PE=PA,PF=PB,∴PA=PB.
(2)作OE⊥PA于点E,OF⊥PB于点F,∴∠OEP=∠OFP=90°. 在△POE和△POF中, ∴△POE≌△POF,∴OE=OF,PE=PF,∴AE=BF,∴PA=PB.
(3)仍有PA=PB.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
