2.9有理数的乘法（3）

(共10张PPT)
第二章 有理数及其运算
§ 有理数的乘法 （3）
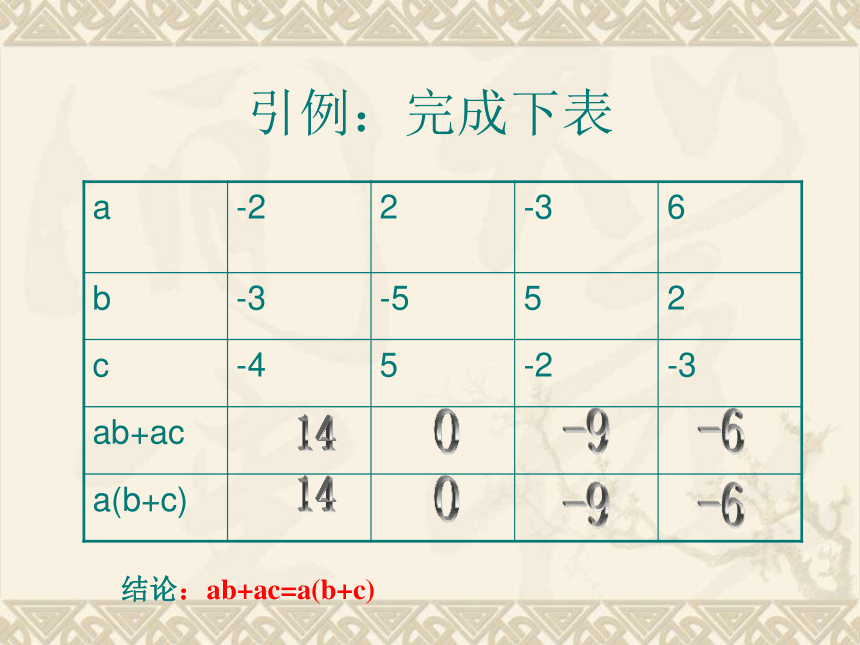
引例：完成下表
a -2 2 -3 6
b -3 -5 5 2
c -4 5 -2 -3
ab+ac
a(b+c)
结论：ab+ac=a(b+c)
练习
5
×
[3+
（
-
7
）
] 5
×
3+5
×（
-
7
）
12
×
[
（
-
3/4
）
+
（
-
4/9
）
] 12
×
(
-
3/4
）
+12
×
（
-
4/9
）
=
一个数同两个数的和相
乘，等于把这
个数分别同这两个数相乘，再把积相加
。
乘法分配律：
a(b+c)=ab+ac
根据分配律可以推出：一个数同几个数的和
相
乘，等于把这个数分别同这几个数相乘，
再把积相加。
=
例题：计算：
解（1）原式=
=11
（2）原式=
（3）原式
= -11
想一想
利用乘法分配律时要注意哪些问题？
形成性测试
一、下列各式变形各用了哪些运算律
？
1
、
1.25
×
(
-
4)
×
(
-
25)
×
8=
(1.25
×
8)
×
[(
-
4)
×
(
-
25)]
2
、（
1/4+2/7-
6/7
）×（
-
8
）
=
（
1/4
）×（
-
8
）
+
（
2/7
-
6/7
）×（
-
8
）
3
、
25
×
[1/3+
（
-
5
）
+2/3]
×（
-
1/5
）
=
25
×（
-
1/5
）×
[
（
-
5
）
+1/3+2/3]
（
乘法交换律和结合律）
（加法结合律和分配律）
（乘法交换律和结合律
）
巧妙计算:
自我检测 ：（10分钟）
计算：
= -370
= 8.24
= 5
= 700
课堂小结:
合理使用乘法交换律，乘法结合律，分配律来解决关于有理数运算中的问题。