2021年人教版初中数学九年级上册24.1.4圆周角 课件(20张)
文档属性
| 名称 | 2021年人教版初中数学九年级上册24.1.4圆周角 课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 631.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 18:03:18 | ||
图片预览






文档简介
(共20张PPT)
人教版《数学》(九年级·上册)
24.1.4圆周角
创设情境,引入新课
问题:
前面我们学习了与圆有关的哪种角 它的特点是什么
(2) 图片欣赏及生活中的实际问题
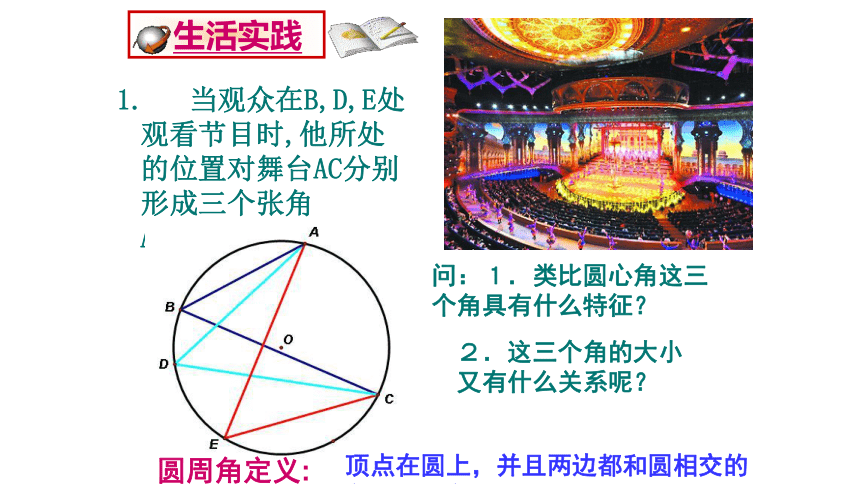
1. 当观众在B,D,E处观看节目时,他所处的位置对舞台AC分别形成三个张角ABC,∠ADC,∠AEC.
生活实践
问:1.类比圆心角这三个角具有什么特征?
2.这三个角的大小又有什么关系呢?
顶点在圆上,并且两边都和圆相交的角叫圆周角.
圆周角定义:
判别下列各图形中的角是不是圆周角。
小试身手
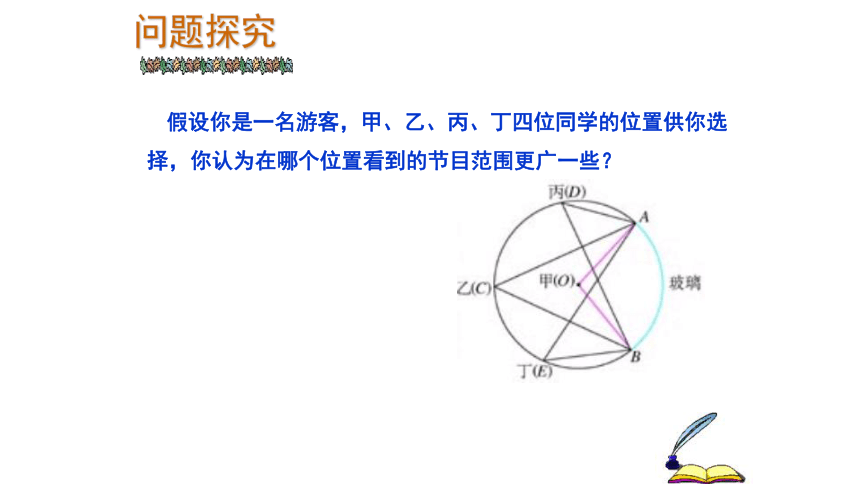
假设你是一名游客,甲、乙、丙、丁四位同学的位置供你选择,你认为在哪个位置看到的节目范围更广一些?
问题探究
自主学习
在之前准备的圆中任意画出一段弧对应的圆周角和圆心角探究中完成:
度量的方法回答下列问题
(1)一条弧所对的圆周角的个数有多少个?
(2)同弧所对的圆周角的度数是否发生变化
(3)同弧所对的圆周角与圆心角有什么关系
我们请同学把所发现的结论用文字语言表述一下。
在同圆或等圆中,同弧所对的圆周角相等,并且都等于这条弧所对的圆心角的一半
根据度量结果和观察结论猜想:
活动探究画一画:请同学们动手画出⊙O中BC所对的圆周角.观察BC所对的圆周角与圆心O有几种位置关系?
学生动手在纸上操作,得出结论
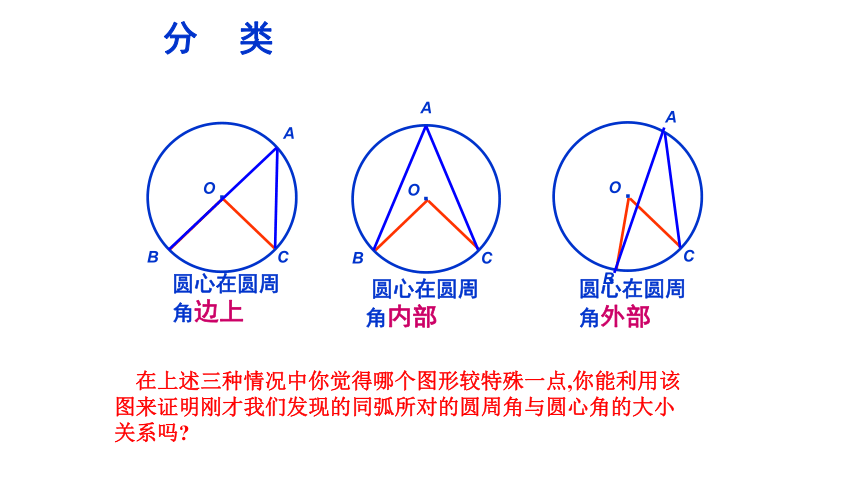
圆周角与圆心的位置关系:
⑴圆心在角的一边上;
⑵圆心在角的内部;
⑶圆心在角的外部。
圆心在圆周角边上
圆心在圆周角内部
圆心在圆周角外部
分 类
C
O
A
·
B
·
C
O
A
B
O
·
C
A
B
在上述三种情况中你觉得哪个图形较特殊一点,你能利用该图来证明刚才我们发现的同弧所对的圆周角与圆心角的大小关系吗
证明∵OA=OC
∴∠A=∠C.
∵∠BOC是△AOC的外角,
∴∠BOC=∠A+∠C.
∴∠BOC=2∠A.
即 ∠BAC = ∠BOC.
证一证
(“红旗”图案)
你能发现几杆类似的“红旗”图案?
这些对该情况下命题的证明有哪些启示?
B
C
A
C
O
A
·
B
·
O
C
A
B
D
D
O
图1
图2
图3
学生完成证明过程,思考交流后一种情况的证明思路,在展示台上展示学生的证明过程,教师做思路和规范性点评)
转化
D
证明思路
A
O
B
C
O
A
B
C
D
圆周角定理:一条弧所对的圆周角等于
这条弧所对的圆心角的一半.
猜想证明
几何语言:
同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.
结论
∵ OA=OC
∴∠A=∠C
又 ∠AOB=∠A+∠C
∴∠AOB= 2∠C
证明:
已知:在⊙O中,AB 所对的圆周角是 ∠C,圆心
角是 ∠AOB. 求证: ∠C = ∠AOB.
(
圆心O在圆周角的一边上
例题分析
即∠C= ∠AOB.
1.已知⊙O的半径OA=4,弦AB=
。
。
2.已知⊙O的半径OA=6,弦AB、AC的长分别为6、6 ,则CAB的度数为30或者90
。
。
3.半径为13CM的⊙O中,弦AB=24CM,弦CD=10CM.AB//CD,则AB、CD间距
离为 17CM或7CM 。
练习
4.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的是( D )
A.50° B.60° C .80° D.100°
5.如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( D )
A.64° B.58° C.32° D.26°
6.已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( D )
A.30° B.60° C.30°或150° D.60°或120°
7.已知在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于D,
BC于E,连接ED.(1)求证:ED=EC;
(2)若CD=3,EC=2,求AB的长.
解:(1)∵∠EDC+∠EDA=180°、∠B+∠EDA=180°,
∴∠B=∠EDC,
又∵AB=AC,∴∠B=∠C,
∴∠EDC=∠C,∴ED=EC;
(2)连接AE,
∵AB是直径,∴AE⊥BC,
又∵AB=AC
∴BC=2EC=4,
∵∠B=∠EDC、∠C=∠C,
∴△ABC∽△EDC,
∴AB:EC=BC:CD,
又∵EC=2、BC=4、CD=3,
∴AB=8.
本节课,你学到了什么?
谢谢
人教版《数学》(九年级·上册)
24.1.4圆周角
创设情境,引入新课
问题:
前面我们学习了与圆有关的哪种角 它的特点是什么
(2) 图片欣赏及生活中的实际问题
1. 当观众在B,D,E处观看节目时,他所处的位置对舞台AC分别形成三个张角ABC,∠ADC,∠AEC.
生活实践
问:1.类比圆心角这三个角具有什么特征?
2.这三个角的大小又有什么关系呢?
顶点在圆上,并且两边都和圆相交的角叫圆周角.
圆周角定义:
判别下列各图形中的角是不是圆周角。
小试身手
假设你是一名游客,甲、乙、丙、丁四位同学的位置供你选择,你认为在哪个位置看到的节目范围更广一些?
问题探究
自主学习
在之前准备的圆中任意画出一段弧对应的圆周角和圆心角探究中完成:
度量的方法回答下列问题
(1)一条弧所对的圆周角的个数有多少个?
(2)同弧所对的圆周角的度数是否发生变化
(3)同弧所对的圆周角与圆心角有什么关系
我们请同学把所发现的结论用文字语言表述一下。
在同圆或等圆中,同弧所对的圆周角相等,并且都等于这条弧所对的圆心角的一半
根据度量结果和观察结论猜想:
活动探究画一画:请同学们动手画出⊙O中BC所对的圆周角.观察BC所对的圆周角与圆心O有几种位置关系?
学生动手在纸上操作,得出结论
圆周角与圆心的位置关系:
⑴圆心在角的一边上;
⑵圆心在角的内部;
⑶圆心在角的外部。
圆心在圆周角边上
圆心在圆周角内部
圆心在圆周角外部
分 类
C
O
A
·
B
·
C
O
A
B
O
·
C
A
B
在上述三种情况中你觉得哪个图形较特殊一点,你能利用该图来证明刚才我们发现的同弧所对的圆周角与圆心角的大小关系吗
证明∵OA=OC
∴∠A=∠C.
∵∠BOC是△AOC的外角,
∴∠BOC=∠A+∠C.
∴∠BOC=2∠A.
即 ∠BAC = ∠BOC.
证一证
(“红旗”图案)
你能发现几杆类似的“红旗”图案?
这些对该情况下命题的证明有哪些启示?
B
C
A
C
O
A
·
B
·
O
C
A
B
D
D
O
图1
图2
图3
学生完成证明过程,思考交流后一种情况的证明思路,在展示台上展示学生的证明过程,教师做思路和规范性点评)
转化
D
证明思路
A
O
B
C
O
A
B
C
D
圆周角定理:一条弧所对的圆周角等于
这条弧所对的圆心角的一半.
猜想证明
几何语言:
同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半.
结论
∵ OA=OC
∴∠A=∠C
又 ∠AOB=∠A+∠C
∴∠AOB= 2∠C
证明:
已知:在⊙O中,AB 所对的圆周角是 ∠C,圆心
角是 ∠AOB. 求证: ∠C = ∠AOB.
(
圆心O在圆周角的一边上
例题分析
即∠C= ∠AOB.
1.已知⊙O的半径OA=4,弦AB=
。
。
2.已知⊙O的半径OA=6,弦AB、AC的长分别为6、6 ,则CAB的度数为30或者90
。
。
3.半径为13CM的⊙O中,弦AB=24CM,弦CD=10CM.AB//CD,则AB、CD间距
离为 17CM或7CM 。
练习
4.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的是( D )
A.50° B.60° C .80° D.100°
5.如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数是( D )
A.64° B.58° C.32° D.26°
6.已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( D )
A.30° B.60° C.30°或150° D.60°或120°
7.已知在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于D,
BC于E,连接ED.(1)求证:ED=EC;
(2)若CD=3,EC=2,求AB的长.
解:(1)∵∠EDC+∠EDA=180°、∠B+∠EDA=180°,
∴∠B=∠EDC,
又∵AB=AC,∴∠B=∠C,
∴∠EDC=∠C,∴ED=EC;
(2)连接AE,
∵AB是直径,∴AE⊥BC,
又∵AB=AC
∴BC=2EC=4,
∵∠B=∠EDC、∠C=∠C,
∴△ABC∽△EDC,
∴AB:EC=BC:CD,
又∵EC=2、BC=4、CD=3,
∴AB=8.
本节课,你学到了什么?
谢谢
同课章节目录
