人教A版数学高二上学期选修2-1第2章 2.4.2抛物线的简单几何性质 课件(26张)
文档属性
| 名称 | 人教A版数学高二上学期选修2-1第2章 2.4.2抛物线的简单几何性质 课件(26张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-11 13:49:10 | ||
图片预览








文档简介
(共26张PPT)
2.4.2 抛物线的简单几何性质
历史回顾
两千多年前,古希腊数学家最先开始研究圆锥曲线,并获得了大量的成果。古希腊数学家阿波罗尼采用平面切割圆锥的方法来研究这几种曲线。用垂直于锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面倾斜到“和且仅和”圆锥的一条母线平行时,得到抛物线;当平面再倾斜一些就可以得到双曲线。阿波罗尼曾把椭圆叫“亏曲线”,把双曲线叫做“超曲线”,把抛物线叫做“齐曲线”。事实上,阿波罗尼在其著作中使用纯几何方法已经取得了今天高中数学中关于圆锥曲线的全部性质和结果。
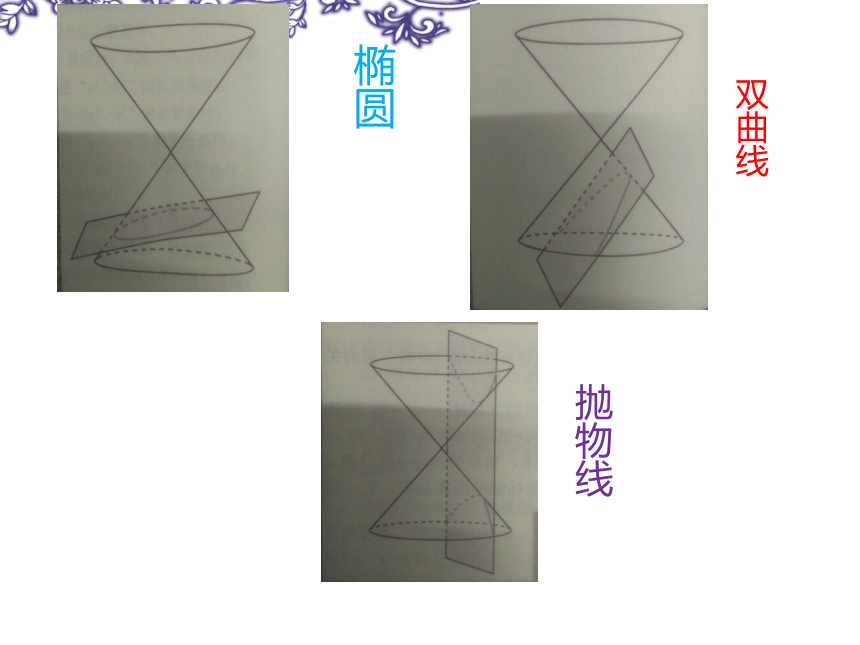
用一个平面去截一个圆锥面,得到的交线就称为圆锥曲线(conic sections)。
通常提到的圆锥曲线包括椭圆,双曲线和抛物线,但严格来讲,它还包括一些退化情形。具体而言:
1) 当平面与圆锥面的母线平行,且不过圆锥顶点,结果为抛物线。
2) 当平面与圆锥面的母线平行,且过圆锥顶点,结果退化为一条直线。
3) 当平面只与圆锥面一侧相交,且不过圆锥顶点,结果为椭圆。
4) 当平面只与圆锥面一侧相交,且不过圆锥顶点,并与圆锥面的对称轴垂直,结果为圆。
5) 当平面只与圆锥面一侧相交,且过圆锥顶点,结果退化为一个点。
6) 当平面与圆锥面两侧都相交,且不过圆锥顶点,结果为双曲线的一支(另一支为此圆锥面的对顶圆锥面与平面的交线)。
7) 当平面与圆锥面两侧都相交,且过圆锥顶点,结果为两条相交直线。
椭圆
双曲线
抛物线
举出生活中的抛物线
一、复习引入
1.二次函数
的图像在a不为0的情况下是一条抛物线,研究顶点,对称轴
二、知识回顾
1.抛物线的定义
在平面内,与一个定点F和一条定直线l(l不经过点F)距
离_____的点的轨迹.
光学性质
从抛物线一个焦点发出的光,经过抛物面反射后,反射光线平行射出
2.抛物线的标准方程
标准 方程 ______ _______ ______ _______
(p>0)p的几何意义:焦点F到准线l的距离 图形
y2=2px
y2=-2px
x2=2py
x2=-2py
焦点 ________ ________ ________ _________
准线 方程 ________ ________ ________ _________
三、新课讲解:
我们根据
抛物线的标准方程
来研究它的一些简单几何性质
y2=2px,p>0
1、范围
p>0,对于抛物线上的点M(x,y),x大于等于0,
抛物线在y轴右边,开口与x轴正向相同·;当x增大,|y|增大,说明无线向右延伸.
2、对称性
以-y代y,所以抛物线关于x轴对称
抛物线的对称轴叫抛物线的轴
3、顶点
抛物线与轴的交点叫抛物线的顶点
4、离心率
抛物线上的点M到焦点和它到准线的距离比叫抛物线的离心率
四、课堂例题陈述:
例题1、已知抛物线关于x轴对称,顶点在坐标原点,,且经过点M(2,-2 ),求标准方程。
例题2、斜率为1的直线经过抛物线 的焦点F,且与抛物线交于A、B两点,求线段AB的长.
答案:8
例题3:求过点(0,1)且与y2=2x有一个交点的直线方程。
答案:
高考题剖析
设抛物线 ,点 , ,过点A的直线L与c交于M,N两点.
(1)当L与x轴垂直时,求直线的方程;
(2)证明: .
解:
(1)
(2)当l与x轴垂直时,AB为MN的垂直平分线,所以∠ABM=∠ABN.
当l与x轴不垂直时,设l的方程为
,M(x1,y1),N(x2,y2),则x1>0,x2>0.
由
得ky2–2y–4k=0,可知y1+y2=,y1y2=–4.
直线BM,BN的斜率之和为
.①
将 , 及y1+y2,y1y2的表达式代入①式分子,可得
.
所以kBM+kBN=0,可知BM,BN的倾斜角互补,所以∠ABM+∠ABN.
综上,∠ABM=∠ABN.
五、课堂练习:
1、已知直线L过点(1,0)且垂直于X轴,若L被抛物线 截得的线段长为4,则抛物线的焦点坐标为_________.
(1,0)
2.已知点 和抛物线 ,过C的焦点且斜率为k的直线与交于A,B两点.若 ,
则k=________.
答案.2
3.(高考题)已知点P是y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.
(1)设AB中点为M,证明:PM垂直于y轴;
(2)若P是半椭圆x2+y2/4=1(x<0)上的动点,求△PAB面积的取值范围.
3.分析:本题主要考查椭圆、抛物线的几何性质,直线与抛物线的位置关系等基础
知识,同时考查运算求解能力和综合应用能力.
解:(1)列出方程。PA,PB中点在抛物线上,方程即 的两个不同的实数根.所以 .因此,PM垂直于轴.
(2)由(1)可知
所以
因为 ,
所以
.
因此,面积的取值范围是 .
六、核心素养归纳:
逻辑推理、数学运算
七、作业:习题B组
END---CLASS IS OVER!
2.4.2 抛物线的简单几何性质
历史回顾
两千多年前,古希腊数学家最先开始研究圆锥曲线,并获得了大量的成果。古希腊数学家阿波罗尼采用平面切割圆锥的方法来研究这几种曲线。用垂直于锥轴的平面去截圆锥,得到的是圆;把平面渐渐倾斜,得到椭圆;当平面倾斜到“和且仅和”圆锥的一条母线平行时,得到抛物线;当平面再倾斜一些就可以得到双曲线。阿波罗尼曾把椭圆叫“亏曲线”,把双曲线叫做“超曲线”,把抛物线叫做“齐曲线”。事实上,阿波罗尼在其著作中使用纯几何方法已经取得了今天高中数学中关于圆锥曲线的全部性质和结果。
用一个平面去截一个圆锥面,得到的交线就称为圆锥曲线(conic sections)。
通常提到的圆锥曲线包括椭圆,双曲线和抛物线,但严格来讲,它还包括一些退化情形。具体而言:
1) 当平面与圆锥面的母线平行,且不过圆锥顶点,结果为抛物线。
2) 当平面与圆锥面的母线平行,且过圆锥顶点,结果退化为一条直线。
3) 当平面只与圆锥面一侧相交,且不过圆锥顶点,结果为椭圆。
4) 当平面只与圆锥面一侧相交,且不过圆锥顶点,并与圆锥面的对称轴垂直,结果为圆。
5) 当平面只与圆锥面一侧相交,且过圆锥顶点,结果退化为一个点。
6) 当平面与圆锥面两侧都相交,且不过圆锥顶点,结果为双曲线的一支(另一支为此圆锥面的对顶圆锥面与平面的交线)。
7) 当平面与圆锥面两侧都相交,且过圆锥顶点,结果为两条相交直线。
椭圆
双曲线
抛物线
举出生活中的抛物线
一、复习引入
1.二次函数
的图像在a不为0的情况下是一条抛物线,研究顶点,对称轴
二、知识回顾
1.抛物线的定义
在平面内,与一个定点F和一条定直线l(l不经过点F)距
离_____的点的轨迹.
光学性质
从抛物线一个焦点发出的光,经过抛物面反射后,反射光线平行射出
2.抛物线的标准方程
标准 方程 ______ _______ ______ _______
(p>0)p的几何意义:焦点F到准线l的距离 图形
y2=2px
y2=-2px
x2=2py
x2=-2py
焦点 ________ ________ ________ _________
准线 方程 ________ ________ ________ _________
三、新课讲解:
我们根据
抛物线的标准方程
来研究它的一些简单几何性质
y2=2px,p>0
1、范围
p>0,对于抛物线上的点M(x,y),x大于等于0,
抛物线在y轴右边,开口与x轴正向相同·;当x增大,|y|增大,说明无线向右延伸.
2、对称性
以-y代y,所以抛物线关于x轴对称
抛物线的对称轴叫抛物线的轴
3、顶点
抛物线与轴的交点叫抛物线的顶点
4、离心率
抛物线上的点M到焦点和它到准线的距离比叫抛物线的离心率
四、课堂例题陈述:
例题1、已知抛物线关于x轴对称,顶点在坐标原点,,且经过点M(2,-2 ),求标准方程。
例题2、斜率为1的直线经过抛物线 的焦点F,且与抛物线交于A、B两点,求线段AB的长.
答案:8
例题3:求过点(0,1)且与y2=2x有一个交点的直线方程。
答案:
高考题剖析
设抛物线 ,点 , ,过点A的直线L与c交于M,N两点.
(1)当L与x轴垂直时,求直线的方程;
(2)证明: .
解:
(1)
(2)当l与x轴垂直时,AB为MN的垂直平分线,所以∠ABM=∠ABN.
当l与x轴不垂直时,设l的方程为
,M(x1,y1),N(x2,y2),则x1>0,x2>0.
由
得ky2–2y–4k=0,可知y1+y2=,y1y2=–4.
直线BM,BN的斜率之和为
.①
将 , 及y1+y2,y1y2的表达式代入①式分子,可得
.
所以kBM+kBN=0,可知BM,BN的倾斜角互补,所以∠ABM+∠ABN.
综上,∠ABM=∠ABN.
五、课堂练习:
1、已知直线L过点(1,0)且垂直于X轴,若L被抛物线 截得的线段长为4,则抛物线的焦点坐标为_________.
(1,0)
2.已知点 和抛物线 ,过C的焦点且斜率为k的直线与交于A,B两点.若 ,
则k=________.
答案.2
3.(高考题)已知点P是y轴左侧(不含y轴)一点,抛物线C:y2=4x上存在不同的两点A,B满足PA,PB的中点均在C上.
(1)设AB中点为M,证明:PM垂直于y轴;
(2)若P是半椭圆x2+y2/4=1(x<0)上的动点,求△PAB面积的取值范围.
3.分析:本题主要考查椭圆、抛物线的几何性质,直线与抛物线的位置关系等基础
知识,同时考查运算求解能力和综合应用能力.
解:(1)列出方程。PA,PB中点在抛物线上,方程即 的两个不同的实数根.所以 .因此,PM垂直于轴.
(2)由(1)可知
所以
因为 ,
所以
.
因此,面积的取值范围是 .
六、核心素养归纳:
逻辑推理、数学运算
七、作业:习题B组
END---CLASS IS OVER!
