2021年北师大版八下数学 3.1图形的平移 教学设计(表格式)
文档属性
| 名称 | 2021年北师大版八下数学 3.1图形的平移 教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 185.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 18:08:32 | ||
图片预览

文档简介
3.1图形的平移 教学设计
授课教师 课题 图形的平移
知识点来源 □学科:数学 □年级:八下 □教材版本:北师大版 □所属章节:第三章 第1节
设计思路 本节课,由生活中常见的平移现象引入,并抽象成数学模型,让学生分析、归纳出平移的概念,渗透数学建模的数学思想。接下来从2个平移的特例出发,通过做一做,画一画,让学生总结平移的基本性质,渗透从特殊到一般的思想方法。最后,在应用中,进一步深化学生对平移变换的理解和认识。
教学设计
内 容
教学目的 通过具体实例认识图形的基本变换-平移变换,并探索平移的基本性质。 能按要求作出简单图形平移后的图形
教学重点难点 教学重点:理解平移的基本性质,能按照要求作出平移后的图形 教学难点:初步应用平移的性质解决问题
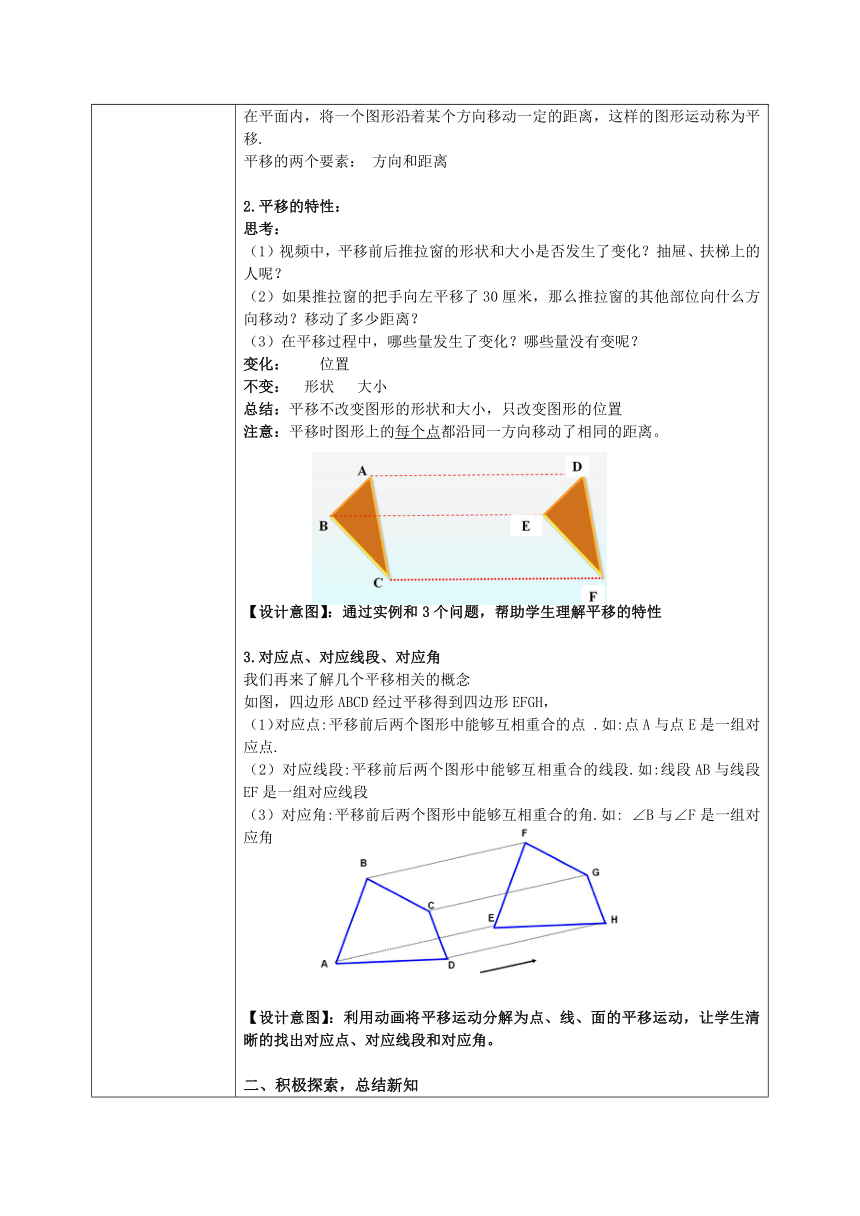
教学过程 问题情境 建立模型 探究 应用 观看视频,导入新知 同学们对平移并不陌生,我们生活中有很多平移的例子,我们首先来观看一段视频。 现在,我们把生活中的例子抽象成数学图形,请同学们观看平移的动画,你能描述一下什么样的图形运动叫做平移吗? 【设计意图】:由学生熟悉的生活经历引入,让学生在轻松、愉快的心情下学习,之后抽象成数学模型研究,渗透数学建模的思想方法。 1.平移的定义: 在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动称为平移. 平移的两个要素: 方向和距离 2.平移的特性: 思考: (1)视频中,平移前后推拉窗的形状和大小是否发生了变化?抽屉、扶梯上的人呢? (2)如果推拉窗的把手向左平移了30厘米,那么推拉窗的其他部位向什么方向移动?移动了多少距离? (3)在平移过程中,哪些量发生了变化?哪些量没有变呢? 变化: 位置 不变: 形状 大小 总结:平移不改变图形的形状和大小,只改变图形的位置 注意:平移时图形上的每个点都沿同一方向移动了相同的距离。 【设计意图】:通过实例和3个问题,帮助学生理解平移的特性 3.对应点、对应线段、对应角 我们再来了解几个平移相关的概念 如图,四边形ABCD经过平移得到四边形EFGH, (1)对应点:平移前后两个图形中能够互相重合的点 .如:点A与点E是一组对应点. (2)对应线段:平移前后两个图形中能够互相重合的线段.如:线段AB与线段EF是一组对应线段 (3)对应角:平移前后两个图形中能够互相重合的角.如: ∠B与∠F是一组对应角 【设计意图】:利用动画将平移运动分解为点、线、面的平移运动,让学生清晰的找出对应点、对应线段和对应角。 二、积极探索,总结新知 做一做: 如上图,四边形ABCD经过平移得到四边形EFGH, (1)任选一组对应线段,它们有怎样的关系? (2)任选一组对应角,它们之间有怎样的关系? (3)线段AE,BF,CG,DH分别是对应点所连成的线段,它们之间有怎样的关系? 初步总结平移的性质 1、平移前后的图形全等 2、 对应线段平行 且相等。 对应点所连的线段平行 且相等. 对应角相等. 同学们看,刚才老师留了2个空白的位置,因为刚才的例子并不能全面表述平移的性质,我们再来看一个例子。 画一画: 用三角板、直尺画平行线. 观察:平移过程中,对应点所连线段有何关系? 平移过程中,对应线段有何关系? 注意:在平移过程中,对应点所连线段可能在同一直线上 (如:BE与CF);对应线段也可能在一条直线上(如:BC与EF) 完善平移的性质: 1、平移前后的图形全等 2、 对应线段平行(或在同一条直线上)且相等。 对应点所连的线段平行(或在同一条直线上)且相等. 对应角相等. 【设计意图】:通过做一做、画一画的2个例子让学生深刻的理解平移的性质,并能全面的对平移性质进行概括。 三、典例精析,应用新知 例:如图,将△ABC沿AA′的方向平移,平移后顶点A平移到A ′处。 (1)指出平移的方向和平移的距离; (2)画出△ABC平移后的图形。 解:(1)连接AA ′,平移的方向是点A到点A ′的方向,平移的距离是线段AA ′的长度。 (2)方法1:利用平移后对应点所连的线段平行且相等 (视频展示画图过程) 想一想:还有其他的方法吗? 方法2:利用平移后对应线段平行且相等 。(课件展示画图过程) 过点A ′按射线AB的方向做线段A ′ B ′平行且等于AB; 过点A ′按射线AC的方向做线段A ′ C ′平行且等于AC; 连接B ′ C ′. ΔA ′ B ′ C ′就是ΔABC平移后的图形. 【设计意图】:让学生学会利用平移的性质解决问题,同时深化对平移性质的理解。 四、课堂小结 本节课我们都学习了哪些内容?你有哪些收获呢? 【设计意图】: 帮助学生回忆和梳理本节课的内容。
授课教师 课题 图形的平移
知识点来源 □学科:数学 □年级:八下 □教材版本:北师大版 □所属章节:第三章 第1节
设计思路 本节课,由生活中常见的平移现象引入,并抽象成数学模型,让学生分析、归纳出平移的概念,渗透数学建模的数学思想。接下来从2个平移的特例出发,通过做一做,画一画,让学生总结平移的基本性质,渗透从特殊到一般的思想方法。最后,在应用中,进一步深化学生对平移变换的理解和认识。
教学设计
内 容
教学目的 通过具体实例认识图形的基本变换-平移变换,并探索平移的基本性质。 能按要求作出简单图形平移后的图形
教学重点难点 教学重点:理解平移的基本性质,能按照要求作出平移后的图形 教学难点:初步应用平移的性质解决问题
教学过程 问题情境 建立模型 探究 应用 观看视频,导入新知 同学们对平移并不陌生,我们生活中有很多平移的例子,我们首先来观看一段视频。 现在,我们把生活中的例子抽象成数学图形,请同学们观看平移的动画,你能描述一下什么样的图形运动叫做平移吗? 【设计意图】:由学生熟悉的生活经历引入,让学生在轻松、愉快的心情下学习,之后抽象成数学模型研究,渗透数学建模的思想方法。 1.平移的定义: 在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动称为平移. 平移的两个要素: 方向和距离 2.平移的特性: 思考: (1)视频中,平移前后推拉窗的形状和大小是否发生了变化?抽屉、扶梯上的人呢? (2)如果推拉窗的把手向左平移了30厘米,那么推拉窗的其他部位向什么方向移动?移动了多少距离? (3)在平移过程中,哪些量发生了变化?哪些量没有变呢? 变化: 位置 不变: 形状 大小 总结:平移不改变图形的形状和大小,只改变图形的位置 注意:平移时图形上的每个点都沿同一方向移动了相同的距离。 【设计意图】:通过实例和3个问题,帮助学生理解平移的特性 3.对应点、对应线段、对应角 我们再来了解几个平移相关的概念 如图,四边形ABCD经过平移得到四边形EFGH, (1)对应点:平移前后两个图形中能够互相重合的点 .如:点A与点E是一组对应点. (2)对应线段:平移前后两个图形中能够互相重合的线段.如:线段AB与线段EF是一组对应线段 (3)对应角:平移前后两个图形中能够互相重合的角.如: ∠B与∠F是一组对应角 【设计意图】:利用动画将平移运动分解为点、线、面的平移运动,让学生清晰的找出对应点、对应线段和对应角。 二、积极探索,总结新知 做一做: 如上图,四边形ABCD经过平移得到四边形EFGH, (1)任选一组对应线段,它们有怎样的关系? (2)任选一组对应角,它们之间有怎样的关系? (3)线段AE,BF,CG,DH分别是对应点所连成的线段,它们之间有怎样的关系? 初步总结平移的性质 1、平移前后的图形全等 2、 对应线段平行 且相等。 对应点所连的线段平行 且相等. 对应角相等. 同学们看,刚才老师留了2个空白的位置,因为刚才的例子并不能全面表述平移的性质,我们再来看一个例子。 画一画: 用三角板、直尺画平行线. 观察:平移过程中,对应点所连线段有何关系? 平移过程中,对应线段有何关系? 注意:在平移过程中,对应点所连线段可能在同一直线上 (如:BE与CF);对应线段也可能在一条直线上(如:BC与EF) 完善平移的性质: 1、平移前后的图形全等 2、 对应线段平行(或在同一条直线上)且相等。 对应点所连的线段平行(或在同一条直线上)且相等. 对应角相等. 【设计意图】:通过做一做、画一画的2个例子让学生深刻的理解平移的性质,并能全面的对平移性质进行概括。 三、典例精析,应用新知 例:如图,将△ABC沿AA′的方向平移,平移后顶点A平移到A ′处。 (1)指出平移的方向和平移的距离; (2)画出△ABC平移后的图形。 解:(1)连接AA ′,平移的方向是点A到点A ′的方向,平移的距离是线段AA ′的长度。 (2)方法1:利用平移后对应点所连的线段平行且相等 (视频展示画图过程) 想一想:还有其他的方法吗? 方法2:利用平移后对应线段平行且相等 。(课件展示画图过程) 过点A ′按射线AB的方向做线段A ′ B ′平行且等于AB; 过点A ′按射线AC的方向做线段A ′ C ′平行且等于AC; 连接B ′ C ′. ΔA ′ B ′ C ′就是ΔABC平移后的图形. 【设计意图】:让学生学会利用平移的性质解决问题,同时深化对平移性质的理解。 四、课堂小结 本节课我们都学习了哪些内容?你有哪些收获呢? 【设计意图】: 帮助学生回忆和梳理本节课的内容。
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
