24.1.4 圆周角 人教版九年级数学上册课时作业(含答案)
文档属性
| 名称 | 24.1.4 圆周角 人教版九年级数学上册课时作业(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 391.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级数学上册课时作业
第二十四章 圆
24.1.4 圆周角
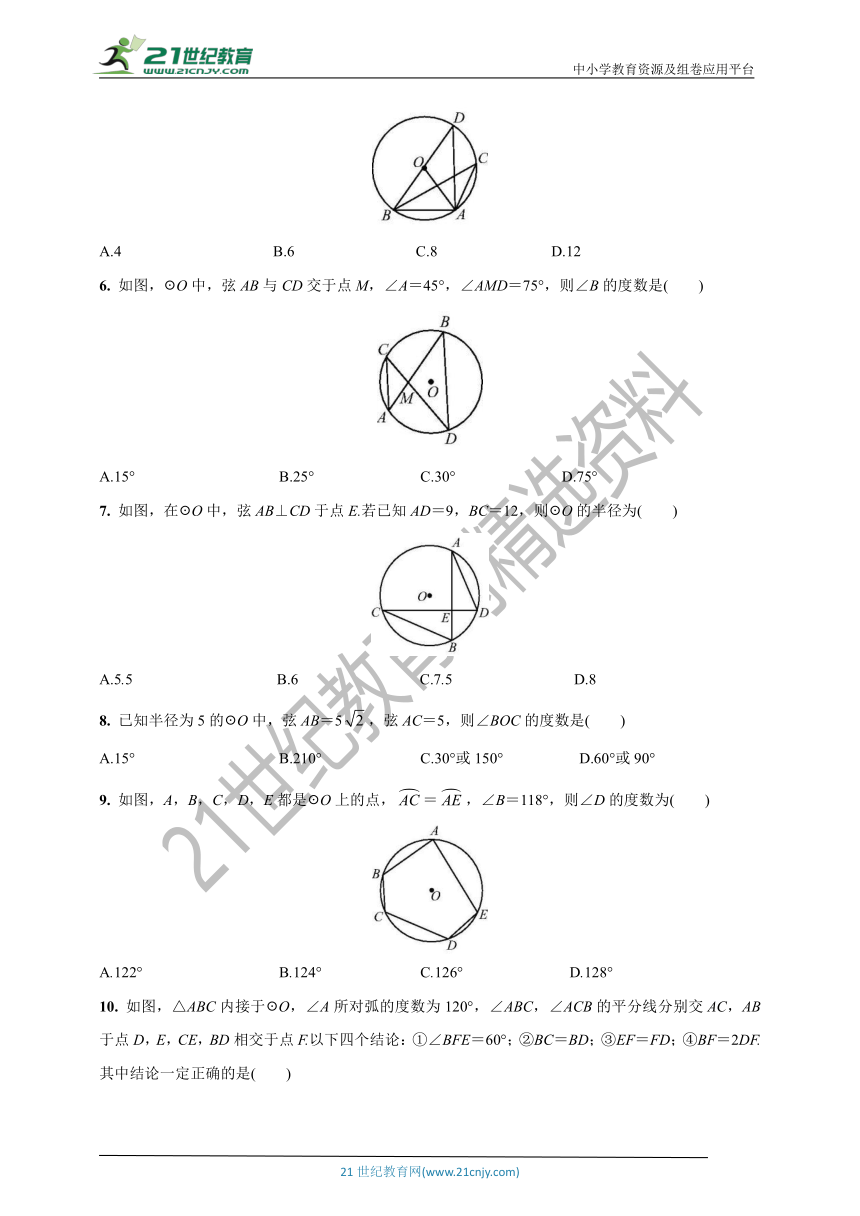
1. 下列图形中的角是圆周角的是( )
A B C D
2. 如图,已知点A,B,C在☉O上,∠A=72°,则∠OBC的度数是( )
A.12° B.15° C.18° D.20°
3. 如图,△ABC的三个顶点都在☉O上,AB经过圆心O,∠A=60°,AC=2,则☉O的直径是( )
A.2 B.4 C. D.2
4. 如图,四边形ABCD为☉O的内接四边形,∠BOD=120°,则∠BCD的大小( )
A.120° B.100° C.80° D.60°
5. 如图,△ABC内接于☉O,∠BAC=120°,AB=AC=6,BD为☉O的直径,则BD等于( )
A.4 B.6 C.8 D.12
6. 如图,☉O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15° B.25° C.30° D.75°
7. 如图,在☉O中,弦AB⊥CD于点E.若已知AD=9,BC=12,则☉O的半径为( )
A.5.5 B.6 C.7.5 D.8
8. 已知半径为5的☉O中,弦AB=5,弦AC=5,则∠BOC的度数是( )
A.15° B.210° C.30°或150° D.60°或90°
9. 如图,A,B,C,D,E都是☉O上的点,=,∠B=118°,则∠D的度数为( )
A.122° B.124° C.126° D.128°
10. 如图,△ABC内接于☉O,∠A所对弧的度数为120°,∠ABC,∠ACB的平分线分别交AC,AB于点D,E,CE,BD相交于点F.以下四个结论:①∠BFE=60°;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的是( )
A.①④ B.①②③ C.①③ D.②③
11. 如图,AB是☉O的直径,点C,D在☉O上,∠AOC=70°,AD∥OC,则∠ABD= .
12. 如图,A,B,C,D四点都在☉O上,若∠C=100°,则∠BAD= ;∠BOD= .
13. 如图,AD是☉O的直径,弦BC与弦CD长度相同,已知∠A=60°,则∠DOC= .
14. 如图,已知AM为☉O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交☉O于点D,E,∠BMD=40°,则∠EOM= .
15. 如图,在△ABC中,AB=AC=5,以AB为直径的☉O与BC交于点D,与AC交于点E,连接OD交BE于点M,且MD=1,则BE的长为 .
16. 如图,AD是☉O的直径,点O是圆心,C,F是AD上的两点,OC=OF,B,E是☉O上的两点,且=.求证:BC∥EF.
17. 如图,☉O的直径AB为10 cm,弦AC为6 cm,且AD=BD.
(1)求BC,AD,BD的长.
(2)图中还有一条线段CD的长是否能确定 若能,求出CD的长.
18. 如图,在锐角△ABC中,AB>AC,AD⊥BC于点D,以AD为直径的☉O分别交AB,AC于点E,F,连接DE,DF.
(1)求证:∠EAF+∠EDF=180°.
(2)已知P是射线DC上的一个动点,当点P运动到PD=BD时,连接AP,交☉O于点G,连接DG.设∠EDG=∠α,∠APB=∠β,那么∠α与∠β有何数量关系 试证明你的结论.
参 考 答 案
1. B 2. C 3. B 4. A 5. D 6. C 7. C 8. C 9. B 10. C
11. 20° 12. 80° 160° 13. 60° 14. 80° 15. 4
16. 证明:∵=,AD是直径,∴AB=DE,=,∴∠A=∠D. ∵OC=OF,OA=OD,∴AC=DF,∴△BAC≌△EDF(SAS),∴∠ACB=∠DFE,∴∠BCF=∠EFC,∴BC∥EF.
17. 解:(1)∵AB是☉O的直径,∴∠ACB=∠ADB=90°. ∵AB=10 cm,AC=6 cm,∴BC=8 cm. ∵AD=BD,∴AD=BD=AB=5cm.
(2)图中线段CD的长能确定.作AE⊥CD于点E. ∵AE⊥CD,∠ACE=∠ABD=45°,∴AE=CE=AC=3cm. 在Rt△AED中,DE==4cm,∴CD=CE+DE=3+4=7cm.
18. 解:(1)在圆内接四边形AEDF中,AD为直径,∴∠AED=∠AFD=90°. 又∵∠AED+∠AFD+∠EAF+∠EDF=360°,∴∠EAF+∠EDF=360°-(∠AED+∠AFD)=180°.
(2)∠α=2∠β. 理由:如图,在△ABD与△APD中,AD⊥BP,且BD=DP,AD=AD,∴△ABD≌△APD(SAS),∴∠B=∠APD=∠β. 在△ABP中,∠EAG+∠B+∠APD=180°,∴∠EAG+2∠β=180°.
由(1)知∠EAG+∠EDG=180°,∴∠EAG+∠α=180°,∴∠α=2∠β.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学上册课时作业
第二十四章 圆
24.1.4 圆周角
1. 下列图形中的角是圆周角的是( )
A B C D
2. 如图,已知点A,B,C在☉O上,∠A=72°,则∠OBC的度数是( )
A.12° B.15° C.18° D.20°
3. 如图,△ABC的三个顶点都在☉O上,AB经过圆心O,∠A=60°,AC=2,则☉O的直径是( )
A.2 B.4 C. D.2
4. 如图,四边形ABCD为☉O的内接四边形,∠BOD=120°,则∠BCD的大小( )
A.120° B.100° C.80° D.60°
5. 如图,△ABC内接于☉O,∠BAC=120°,AB=AC=6,BD为☉O的直径,则BD等于( )
A.4 B.6 C.8 D.12
6. 如图,☉O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是( )
A.15° B.25° C.30° D.75°
7. 如图,在☉O中,弦AB⊥CD于点E.若已知AD=9,BC=12,则☉O的半径为( )
A.5.5 B.6 C.7.5 D.8
8. 已知半径为5的☉O中,弦AB=5,弦AC=5,则∠BOC的度数是( )
A.15° B.210° C.30°或150° D.60°或90°
9. 如图,A,B,C,D,E都是☉O上的点,=,∠B=118°,则∠D的度数为( )
A.122° B.124° C.126° D.128°
10. 如图,△ABC内接于☉O,∠A所对弧的度数为120°,∠ABC,∠ACB的平分线分别交AC,AB于点D,E,CE,BD相交于点F.以下四个结论:①∠BFE=60°;②BC=BD;③EF=FD;④BF=2DF.其中结论一定正确的是( )
A.①④ B.①②③ C.①③ D.②③
11. 如图,AB是☉O的直径,点C,D在☉O上,∠AOC=70°,AD∥OC,则∠ABD= .
12. 如图,A,B,C,D四点都在☉O上,若∠C=100°,则∠BAD= ;∠BOD= .
13. 如图,AD是☉O的直径,弦BC与弦CD长度相同,已知∠A=60°,则∠DOC= .
14. 如图,已知AM为☉O的直径,直线BC经过点M,且AB=AC,∠BAM=∠CAM,线段AB和AC分别交☉O于点D,E,∠BMD=40°,则∠EOM= .
15. 如图,在△ABC中,AB=AC=5,以AB为直径的☉O与BC交于点D,与AC交于点E,连接OD交BE于点M,且MD=1,则BE的长为 .
16. 如图,AD是☉O的直径,点O是圆心,C,F是AD上的两点,OC=OF,B,E是☉O上的两点,且=.求证:BC∥EF.
17. 如图,☉O的直径AB为10 cm,弦AC为6 cm,且AD=BD.
(1)求BC,AD,BD的长.
(2)图中还有一条线段CD的长是否能确定 若能,求出CD的长.
18. 如图,在锐角△ABC中,AB>AC,AD⊥BC于点D,以AD为直径的☉O分别交AB,AC于点E,F,连接DE,DF.
(1)求证:∠EAF+∠EDF=180°.
(2)已知P是射线DC上的一个动点,当点P运动到PD=BD时,连接AP,交☉O于点G,连接DG.设∠EDG=∠α,∠APB=∠β,那么∠α与∠β有何数量关系 试证明你的结论.
参 考 答 案
1. B 2. C 3. B 4. A 5. D 6. C 7. C 8. C 9. B 10. C
11. 20° 12. 80° 160° 13. 60° 14. 80° 15. 4
16. 证明:∵=,AD是直径,∴AB=DE,=,∴∠A=∠D. ∵OC=OF,OA=OD,∴AC=DF,∴△BAC≌△EDF(SAS),∴∠ACB=∠DFE,∴∠BCF=∠EFC,∴BC∥EF.
17. 解:(1)∵AB是☉O的直径,∴∠ACB=∠ADB=90°. ∵AB=10 cm,AC=6 cm,∴BC=8 cm. ∵AD=BD,∴AD=BD=AB=5cm.
(2)图中线段CD的长能确定.作AE⊥CD于点E. ∵AE⊥CD,∠ACE=∠ABD=45°,∴AE=CE=AC=3cm. 在Rt△AED中,DE==4cm,∴CD=CE+DE=3+4=7cm.
18. 解:(1)在圆内接四边形AEDF中,AD为直径,∴∠AED=∠AFD=90°. 又∵∠AED+∠AFD+∠EAF+∠EDF=360°,∴∠EAF+∠EDF=360°-(∠AED+∠AFD)=180°.
(2)∠α=2∠β. 理由:如图,在△ABD与△APD中,AD⊥BP,且BD=DP,AD=AD,∴△ABD≌△APD(SAS),∴∠B=∠APD=∠β. 在△ABP中,∠EAG+∠B+∠APD=180°,∴∠EAG+2∠β=180°.
由(1)知∠EAG+∠EDG=180°,∴∠EAG+∠α=180°,∴∠α=2∠β.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
