2021-2022学年北京课改版数学八年级上册第十二章 三角形期末测试试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年北京课改版数学八年级上册第十二章 三角形期末测试试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 292.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 10:31:46 | ||
图片预览

文档简介
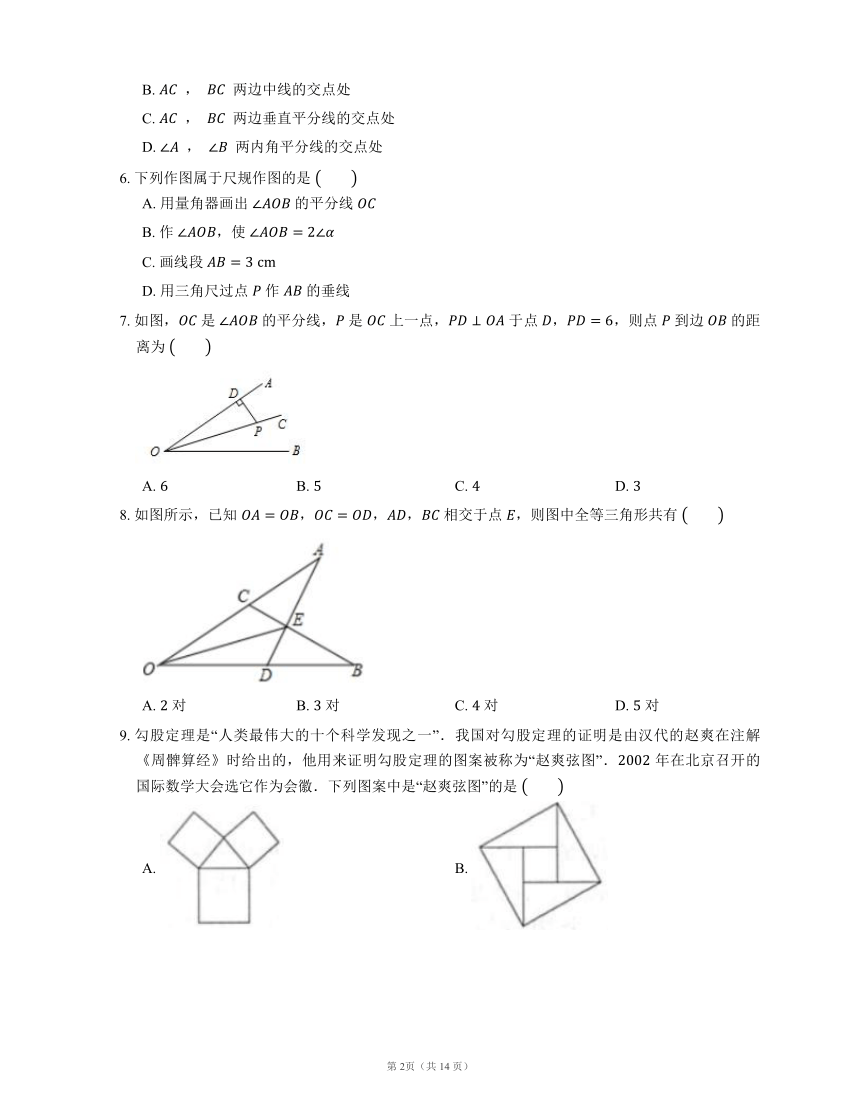
第十二章 三角形
一、选择题(共10小题;共50分)
1. 下列各组线段中,能组成三角形的是
A. ,, B. ,, C. ,, D. ,,
2. 如果 的三边长分别为 的三边长分别为 , , 若这两个三角形全等,则 ()
A. 8 B. 或 6 C. 10 D. 或 6
3. 如图, 与 关于直线 对称,则 的度数为
A. B. C. D.
4. 如图,下列说法错误的是
A. ,, 是 的内角
B. 是与 相邻的角
C.
D. 的三条边分别是 ,,
5. 如图所示,,, 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在
A. , 两边高线的交点处
B. , 两边中线的交点处
C. , 两边垂直平分线的交点处
D. , 两内角平分线的交点处
6. 下列作图属于尺规作图的是
A. 用量角器画出 的平分线
B. 作 ,使
C. 画线段
D. 用三角尺过点 作 的垂线
7. 如图, 是 的平分线, 是 上一点, 于点 ,,则点 到边 的距离为
A. B. C. D.
8. 如图所示,已知 ,,, 相交于点 ,则图中全等三角形共有
A. 对 B. 对 C. 对 D. 对
9. 勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”. 年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是
A. B.
C. D.
10. 如图,等边 中, 于 ,,点 , 分别为 , 上的两个定点且 ,在 上有一动点 使 最短,则 的最小值为
A. B. C. D.
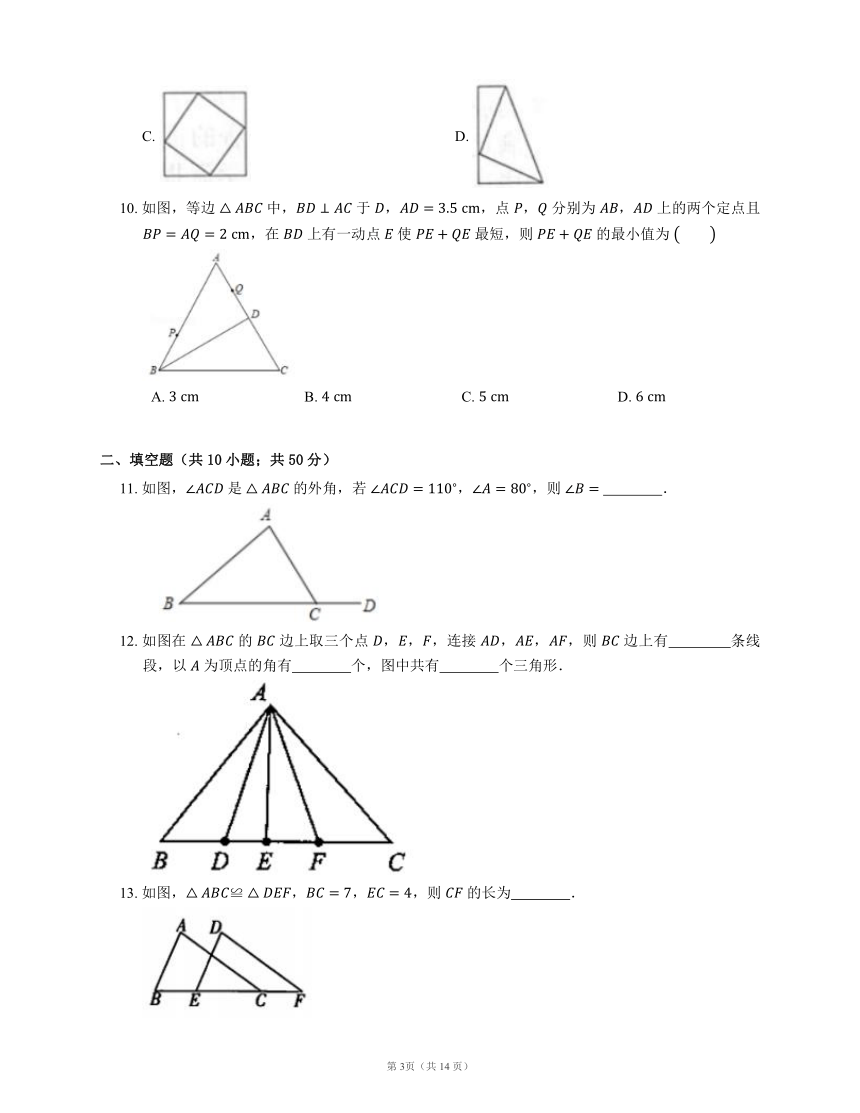
二、填空题(共10小题;共50分)
11. 如图, 是 的外角,若 ,,则 .
12. 如图在 的 边上取三个点 ,,,连接 ,,,则 边上有 条线段,以 为顶点的角有 个,图中共有 个三角形.
13. 如图,,,,则 的长为 .
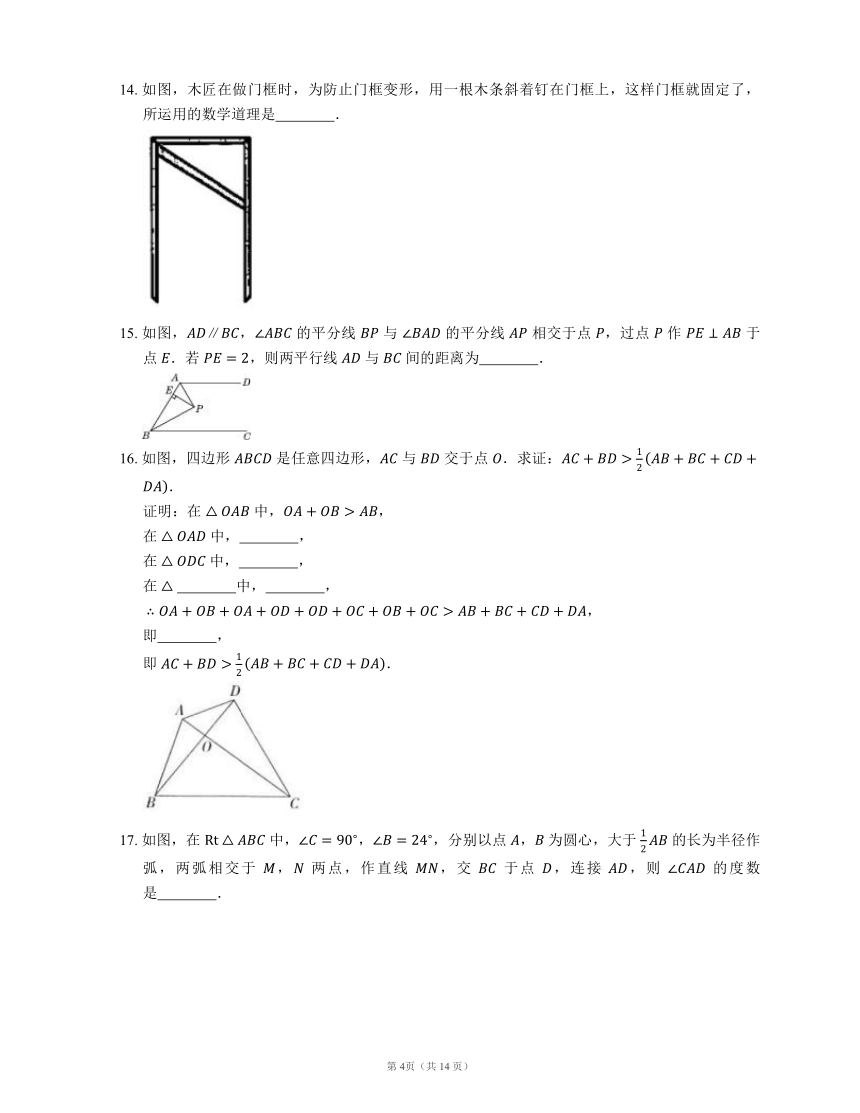
14. 如图,木匠在做门框时,为防止门框变形,用一根木条斜着钉在门框上,这样门框就固定了,所运用的数学道理是 .
15. 如图,, 的平分线 与 的平分线 相交于点 ,过点 作 于点 .若 ,则两平行线 与 间的距离为 .
16. 如图,四边形 是任意四边形, 与 交于点 .求证:.
证明:在 中,,
在 中, ,
在 中, ,
在 中, ,
,
即 ,
即 .
17. 如图,在 中,,,分别以点 , 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 ,交 于点 ,连接 ,则 的度数是 .
18. 一个三角形的三边长 ,, 满足 ,则这个三角形最长边上的高为 .
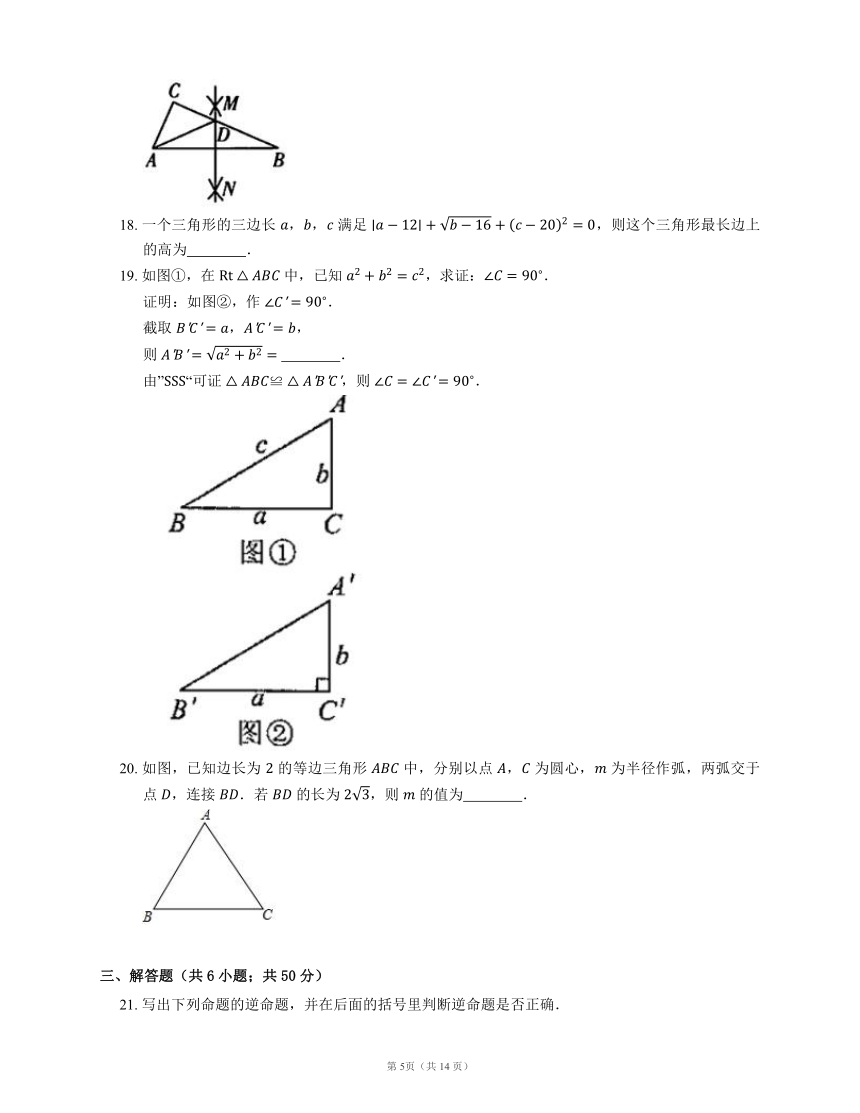
19. 如图①,在 中,已知 ,求证:.
证明:如图②,作 .
截取 ,,
则 .
由”“可证 ,则 .
20. 如图,已知边长为 的等边三角形 中,分别以点 , 为圆心, 为半径作弧,两弧交于点 ,连接 .若 的长为 ,则 的值为 .
三、解答题(共6小题;共50分)
21. 写出下列命题的逆命题,并在后面的括号里判断逆命题是否正确.
(1)同旁内角互补,两直线平行;
( )
(2)全等三角形的对应角相等.
( )
22. 已知 的面积为 ,斜边长为 ,两直角边长分别为 ,.求代数式 的值.
23. 如图,在 的方格中有一个四边形和两个三角形(所有顶点都在方格的格点上)
(1)请你画出三个图形关于直线 的对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数.
24. 如图,在 中,,.
求证: 是直角三角形.
25. 如图, 是 的高, 的垂直平分线分别交 , 于点 ,, 与 交于点 .求证:.
26. 如图,直线 于点 , 是直角三角形,,斜边 交直线 于点 , 平分 , 的平分线交 的反向延长线于点 ,.
(1)如图①,当 时,求 的度数;
(2)如图②,将 绕 点旋转一定的角度( 与 不平行),其他条件不变, 的度数是否改变 请说明理由.
答案
第一部分
1. C
2. D 【解析】略
3. D
4. C 【解析】.
5. C
【解析】根据到线段两端距离相等的点在线段的垂直平分线上,得到三角形三个顶点的距离相等的点一定是三角形任意两边的垂直平分线的交点.
6. B 【解析】尺规作图是只限于用没有刻度的直尺和圆规画的图.
7. A
8. C 【解析】在 和 中,
;
,
,,
,
在 和 中,
;
;
在 和 中,
;
在 和 中,
;
9. B 【解析】“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,
10. C
【解析】如图,
是等边三角形,
,
,
,
作点 关于 的对称点 ,连接 交 于 ,连接 ,此时 的值最小.最小值 ,
,
,
,
,
,
是等边三角形,
,
的最小值为 .
第二部分
11.
【解析】,,
,
故答案为:.
12. ,,
13.
14. 三角形具有稳定性
15.
【解析】如图,过点 作 ,交 于点 ,交 于点 .
, 的平分线 与 的平分线 相交于点 ,
,.
又 ,
,,
.
16. ,,,,
17.
18.
【解析】由题意得 ,,,
解得 ,,.
因为 ,
所以该三角形为直角三角形, 为斜边.
设斜边上的高为 ,由面积公式得 ,
所以 .
19. c
20. 或
【解析】由作图知,点 在 的垂直平分线上,
是等边三角形,
点 在 的垂直平分线上,
垂直平分 ,
设垂足为 ,
,
,
当点 , 在 的两侧时,如图,
,
,
,
;
当点 , 在 的同侧时,如图,
,
,
,
.
综上所述, 的值为 或 .
第三部分
21. (1) 两直线平行,同旁内角互补;正确
(2) 对应角相等的三角形全等;不正确
22. 的面积为 ,
,
解得 ,
根据勾股定理得:,
.
23. (1) 所画图形如下所示:
(2) 这个整体图形共有 条对称轴.
24. 如图,作 平分 交 于点 ,过 作 于点 .
平分 ,
,
,
,
是等腰三角形,
又 ,
.
,
.
在 与 中,
.
,
是直角三角形.
25. 是 的垂直平分线,
,.
在 和 中,
,
.
是 的高,
.
又 ,
,
,
.
26. (1) 如图,
因为 ,
所以 .
因为 平分 ,
所以 ,
因为 ,
所以 ,
所以 ,
因为 ,
所以 ,
因为 平分 ,
所以 ,
因为 为 的外角,
所以 .
(2) 的度数不变.理由如下:
如图,
设 ,
所以 ,
所以 ,
因为 平分 ,
所以 ,
所以 .
第1页(共3 页)
一、选择题(共10小题;共50分)
1. 下列各组线段中,能组成三角形的是
A. ,, B. ,, C. ,, D. ,,
2. 如果 的三边长分别为 的三边长分别为 , , 若这两个三角形全等,则 ()
A. 8 B. 或 6 C. 10 D. 或 6
3. 如图, 与 关于直线 对称,则 的度数为
A. B. C. D.
4. 如图,下列说法错误的是
A. ,, 是 的内角
B. 是与 相邻的角
C.
D. 的三条边分别是 ,,
5. 如图所示,,, 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在
A. , 两边高线的交点处
B. , 两边中线的交点处
C. , 两边垂直平分线的交点处
D. , 两内角平分线的交点处
6. 下列作图属于尺规作图的是
A. 用量角器画出 的平分线
B. 作 ,使
C. 画线段
D. 用三角尺过点 作 的垂线
7. 如图, 是 的平分线, 是 上一点, 于点 ,,则点 到边 的距离为
A. B. C. D.
8. 如图所示,已知 ,,, 相交于点 ,则图中全等三角形共有
A. 对 B. 对 C. 对 D. 对
9. 勾股定理是“人类最伟大的十个科学发现之一”.我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”. 年在北京召开的国际数学大会选它作为会徽.下列图案中是“赵爽弦图”的是
A. B.
C. D.
10. 如图,等边 中, 于 ,,点 , 分别为 , 上的两个定点且 ,在 上有一动点 使 最短,则 的最小值为
A. B. C. D.
二、填空题(共10小题;共50分)
11. 如图, 是 的外角,若 ,,则 .
12. 如图在 的 边上取三个点 ,,,连接 ,,,则 边上有 条线段,以 为顶点的角有 个,图中共有 个三角形.
13. 如图,,,,则 的长为 .
14. 如图,木匠在做门框时,为防止门框变形,用一根木条斜着钉在门框上,这样门框就固定了,所运用的数学道理是 .
15. 如图,, 的平分线 与 的平分线 相交于点 ,过点 作 于点 .若 ,则两平行线 与 间的距离为 .
16. 如图,四边形 是任意四边形, 与 交于点 .求证:.
证明:在 中,,
在 中, ,
在 中, ,
在 中, ,
,
即 ,
即 .
17. 如图,在 中,,,分别以点 , 为圆心,大于 的长为半径作弧,两弧相交于 , 两点,作直线 ,交 于点 ,连接 ,则 的度数是 .
18. 一个三角形的三边长 ,, 满足 ,则这个三角形最长边上的高为 .
19. 如图①,在 中,已知 ,求证:.
证明:如图②,作 .
截取 ,,
则 .
由”“可证 ,则 .
20. 如图,已知边长为 的等边三角形 中,分别以点 , 为圆心, 为半径作弧,两弧交于点 ,连接 .若 的长为 ,则 的值为 .
三、解答题(共6小题;共50分)
21. 写出下列命题的逆命题,并在后面的括号里判断逆命题是否正确.
(1)同旁内角互补,两直线平行;
( )
(2)全等三角形的对应角相等.
( )
22. 已知 的面积为 ,斜边长为 ,两直角边长分别为 ,.求代数式 的值.
23. 如图,在 的方格中有一个四边形和两个三角形(所有顶点都在方格的格点上)
(1)请你画出三个图形关于直线 的对称图形;
(2)将(1)中画出的图形与原图形看成一个整体图形,请写出这个整体图形对称轴的条数.
24. 如图,在 中,,.
求证: 是直角三角形.
25. 如图, 是 的高, 的垂直平分线分别交 , 于点 ,, 与 交于点 .求证:.
26. 如图,直线 于点 , 是直角三角形,,斜边 交直线 于点 , 平分 , 的平分线交 的反向延长线于点 ,.
(1)如图①,当 时,求 的度数;
(2)如图②,将 绕 点旋转一定的角度( 与 不平行),其他条件不变, 的度数是否改变 请说明理由.
答案
第一部分
1. C
2. D 【解析】略
3. D
4. C 【解析】.
5. C
【解析】根据到线段两端距离相等的点在线段的垂直平分线上,得到三角形三个顶点的距离相等的点一定是三角形任意两边的垂直平分线的交点.
6. B 【解析】尺规作图是只限于用没有刻度的直尺和圆规画的图.
7. A
8. C 【解析】在 和 中,
;
,
,,
,
在 和 中,
;
;
在 和 中,
;
在 和 中,
;
9. B 【解析】“赵爽弦图”是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形,
10. C
【解析】如图,
是等边三角形,
,
,
,
作点 关于 的对称点 ,连接 交 于 ,连接 ,此时 的值最小.最小值 ,
,
,
,
,
,
是等边三角形,
,
的最小值为 .
第二部分
11.
【解析】,,
,
故答案为:.
12. ,,
13.
14. 三角形具有稳定性
15.
【解析】如图,过点 作 ,交 于点 ,交 于点 .
, 的平分线 与 的平分线 相交于点 ,
,.
又 ,
,,
.
16. ,,,,
17.
18.
【解析】由题意得 ,,,
解得 ,,.
因为 ,
所以该三角形为直角三角形, 为斜边.
设斜边上的高为 ,由面积公式得 ,
所以 .
19. c
20. 或
【解析】由作图知,点 在 的垂直平分线上,
是等边三角形,
点 在 的垂直平分线上,
垂直平分 ,
设垂足为 ,
,
,
当点 , 在 的两侧时,如图,
,
,
,
;
当点 , 在 的同侧时,如图,
,
,
,
.
综上所述, 的值为 或 .
第三部分
21. (1) 两直线平行,同旁内角互补;正确
(2) 对应角相等的三角形全等;不正确
22. 的面积为 ,
,
解得 ,
根据勾股定理得:,
.
23. (1) 所画图形如下所示:
(2) 这个整体图形共有 条对称轴.
24. 如图,作 平分 交 于点 ,过 作 于点 .
平分 ,
,
,
,
是等腰三角形,
又 ,
.
,
.
在 与 中,
.
,
是直角三角形.
25. 是 的垂直平分线,
,.
在 和 中,
,
.
是 的高,
.
又 ,
,
,
.
26. (1) 如图,
因为 ,
所以 .
因为 平分 ,
所以 ,
因为 ,
所以 ,
所以 ,
因为 ,
所以 ,
因为 平分 ,
所以 ,
因为 为 的外角,
所以 .
(2) 的度数不变.理由如下:
如图,
设 ,
所以 ,
所以 ,
因为 平分 ,
所以 ,
所以 .
第1页(共3 页)
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
