24.2.1 点和圆的位置关系 人教版九年级数学上册课时作业(含答案)
文档属性
| 名称 | 24.2.1 点和圆的位置关系 人教版九年级数学上册课时作业(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 265.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-09 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
人教版九年级数学上册课时作业
第二十四章 圆
24.2.1 点和圆的位置关系
1. ☉O的直径为4,点A到圆心O的距离为3,则( )
A.点A在☉O外 B.点A在☉O上
C.点A在☉O内 D.点A与☉O的位置关系不能确定
2. 确定一个圆的条件是( )
A.已知圆心 B.已知半径
C.过三个已知点 D.过一个三角形的三个顶点
3. 过钝角三角形的三个顶点作圆,其圆心在( )
A.三角形内 B.三角形上 C.三角形外 D.以上都有可能
4. 用反证法证明“a不大于b”时,第一步应假设( )
A.a>b B.a=b C.a≥b D.a≠b
5. 若☉A的半径为5,圆心A的坐标是(1,2),点P的坐标是(5,2),那么点P的位置为( )
A.在☉A内 B.在☉A上 C.在☉A外 D.不能确定
6. 如图所示,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,☉A的半径为3,那么下列说法正确的是( )
A.点B,点C都在☉A内 B.点C在☉A内,点B在☉A外
C.点B在☉A内,点C在☉A外 D.点B,点C都在☉A外
7. 如图,△ABC内接于☉O,∠BAC=30°,BC=8,则☉O的半径为( )
A.4 B.6 C.8 D.12
8. 用反证法证明“在△ABC中,∠A,∠B的对边分别是a,b,若∠A>∠B,则a>b.”第一步应假( )
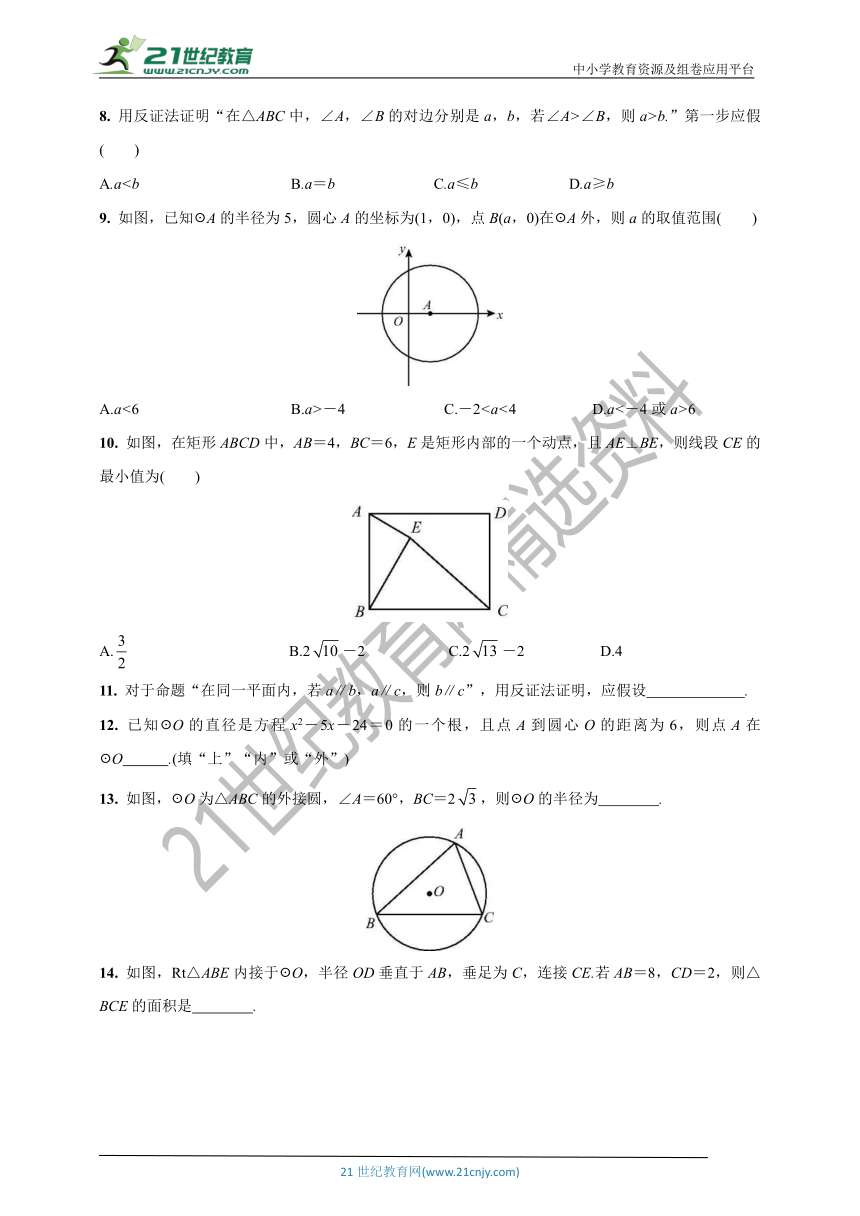
A.a9. 如图,已知☉A的半径为5,圆心A的坐标为(1,0),点B(a,0)在☉A外,则a的取值范围( )
A.a<6 B.a>-4 C.-26
10. 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( )
A. B.2-2 C.2-2 D.4
11. 对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设 .
12. 已知☉O的直径是方程x2-5x-24=0的一个根,且点A到圆心O的距离为6,则点A在☉O .(填“上”“内”或“外”)
13. 如图,☉O为△ABC的外接圆,∠A=60°,BC=2,则☉O的半径为 .
14. 如图,Rt△ABE内接于☉O,半径OD垂直于AB,垂足为C,连接CE.若AB=8,CD=2,则△BCE的面积是 .
15. 如图,△ABC内接于☉O,AD⊥BC于点D,AD=BD.若☉O的半径OB=2,则AC的长为 .
16. 如图所示,已知矩形ABCD的边AB=3 cm,AD=4 cm.
(1)以点A为圆心、4 cm为半径作☉A,则点B,C,D与☉A的位置关系如何
(2)若以点A为圆心作☉A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,则☉A的半径r的取值范围是什么
17. 如图,点B在直线AC上,点D在直线AC外,过A,B,C,D四点中的任意3个点,可以画多少个圆
18. 如图,△ABC内接于☉O,BD为☉O的直径,∠BAC=120°,OA⊥BC.若AB=4,
(1)求证:四边形OACD为菱形;
(2)求AD的长.
参 考 答 案
1. A 2. D 3. C 4. A 5. A 6. D 7. C 8. C 9. D 10. B
11. b与c相交 12. 外 13. 2 14. 12 15. 2
16. 解:(1)点B在☉A内,点D在☉A上,点C在☉A外.
(2)☉A的半径r的取值范围是317. 解:∵点A,B,C在同一条直线上,∴经过点A,B,D或点A,C,D或点B,C,D分别能画一个圆,即经过四点中的任意3个点共能画3个圆.
18. 解:(1)∵OA⊥BC,∴=,∴∠CDA=∠ADB=∠BDC. ∵∠BDC=180°-120°=60°,∴∠CDA=∠ADB=30°. ∵∠CAD=∠CAB-∠BAD=30°,∴∠CAD=∠ADB,∴AC∥OD. 又∵∠DCB=∠OEB=90°,∴CD∥OA,∴四边形OACD为平行四边形. 又∵OA=OD,∴四边形OACD为菱形.
(2)由(1)可知BD=2AB=8,在Rt△ABD中,AD==4.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版九年级数学上册课时作业
第二十四章 圆
24.2.1 点和圆的位置关系
1. ☉O的直径为4,点A到圆心O的距离为3,则( )
A.点A在☉O外 B.点A在☉O上
C.点A在☉O内 D.点A与☉O的位置关系不能确定
2. 确定一个圆的条件是( )
A.已知圆心 B.已知半径
C.过三个已知点 D.过一个三角形的三个顶点
3. 过钝角三角形的三个顶点作圆,其圆心在( )
A.三角形内 B.三角形上 C.三角形外 D.以上都有可能
4. 用反证法证明“a不大于b”时,第一步应假设( )
A.a>b B.a=b C.a≥b D.a≠b
5. 若☉A的半径为5,圆心A的坐标是(1,2),点P的坐标是(5,2),那么点P的位置为( )
A.在☉A内 B.在☉A上 C.在☉A外 D.不能确定
6. 如图所示,在Rt△ABC中,∠C=90°,BC=2,∠B=60°,☉A的半径为3,那么下列说法正确的是( )
A.点B,点C都在☉A内 B.点C在☉A内,点B在☉A外
C.点B在☉A内,点C在☉A外 D.点B,点C都在☉A外
7. 如图,△ABC内接于☉O,∠BAC=30°,BC=8,则☉O的半径为( )
A.4 B.6 C.8 D.12
8. 用反证法证明“在△ABC中,∠A,∠B的对边分别是a,b,若∠A>∠B,则a>b.”第一步应假( )
A.a9. 如图,已知☉A的半径为5,圆心A的坐标为(1,0),点B(a,0)在☉A外,则a的取值范围( )
A.a<6 B.a>-4 C.-2
10. 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为( )
A. B.2-2 C.2-2 D.4
11. 对于命题“在同一平面内,若a∥b,a∥c,则b∥c”,用反证法证明,应假设 .
12. 已知☉O的直径是方程x2-5x-24=0的一个根,且点A到圆心O的距离为6,则点A在☉O .(填“上”“内”或“外”)
13. 如图,☉O为△ABC的外接圆,∠A=60°,BC=2,则☉O的半径为 .
14. 如图,Rt△ABE内接于☉O,半径OD垂直于AB,垂足为C,连接CE.若AB=8,CD=2,则△BCE的面积是 .
15. 如图,△ABC内接于☉O,AD⊥BC于点D,AD=BD.若☉O的半径OB=2,则AC的长为 .
16. 如图所示,已知矩形ABCD的边AB=3 cm,AD=4 cm.
(1)以点A为圆心、4 cm为半径作☉A,则点B,C,D与☉A的位置关系如何
(2)若以点A为圆心作☉A,使B,C,D三点中至少有一个点在圆内,且至少有一点在圆外,则☉A的半径r的取值范围是什么
17. 如图,点B在直线AC上,点D在直线AC外,过A,B,C,D四点中的任意3个点,可以画多少个圆
18. 如图,△ABC内接于☉O,BD为☉O的直径,∠BAC=120°,OA⊥BC.若AB=4,
(1)求证:四边形OACD为菱形;
(2)求AD的长.
参 考 答 案
1. A 2. D 3. C 4. A 5. A 6. D 7. C 8. C 9. D 10. B
11. b与c相交 12. 外 13. 2 14. 12 15. 2
16. 解:(1)点B在☉A内,点D在☉A上,点C在☉A外.
(2)☉A的半径r的取值范围是3
18. 解:(1)∵OA⊥BC,∴=,∴∠CDA=∠ADB=∠BDC. ∵∠BDC=180°-120°=60°,∴∠CDA=∠ADB=30°. ∵∠CAD=∠CAB-∠BAD=30°,∴∠CAD=∠ADB,∴AC∥OD. 又∵∠DCB=∠OEB=90°,∴CD∥OA,∴四边形OACD为平行四边形. 又∵OA=OD,∴四边形OACD为菱形.
(2)由(1)可知BD=2AB=8,在Rt△ABD中,AD==4.
21世纪教育网 www。21cnjy。com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
