高一数学《131 函数的单调性》课件(人教版必修一)
文档属性
| 名称 | 高一数学《131 函数的单调性》课件(人教版必修一) |  | |
| 格式 | zip | ||
| 文件大小 | 237.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-18 08:26:48 | ||
图片预览






文档简介
(共40张PPT)
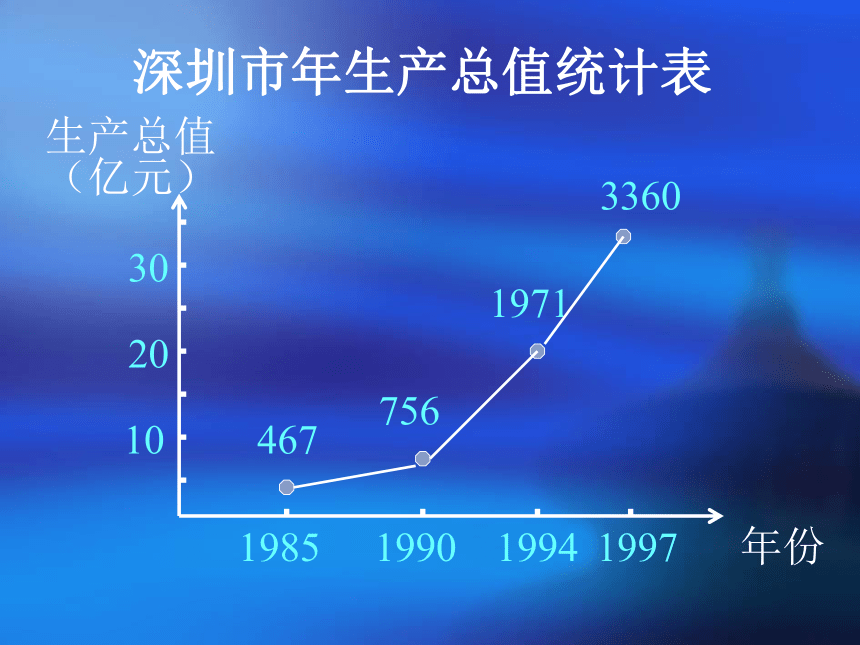
深圳市年生产总值统计表
年份
生产总值
(亿元)
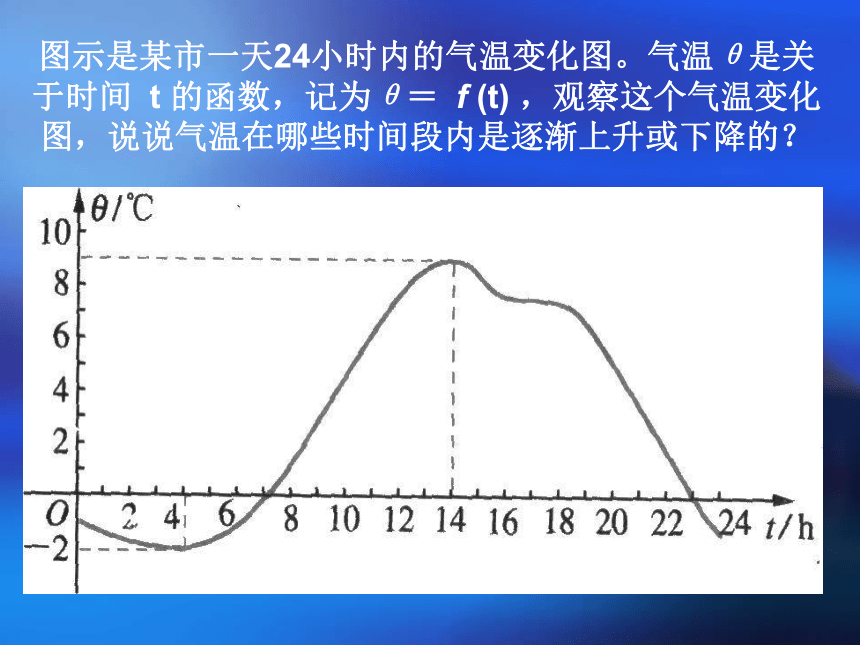
图示是某市一天24小时内的气温变化图。气温θ是关于时间 t 的函数,记为θ= f (t) ,观察这个气温变化图,说说气温在哪些时间段内是逐渐上升或下降的?
O
x
y
O
x
y
O
x
y
2
1
y
O
x
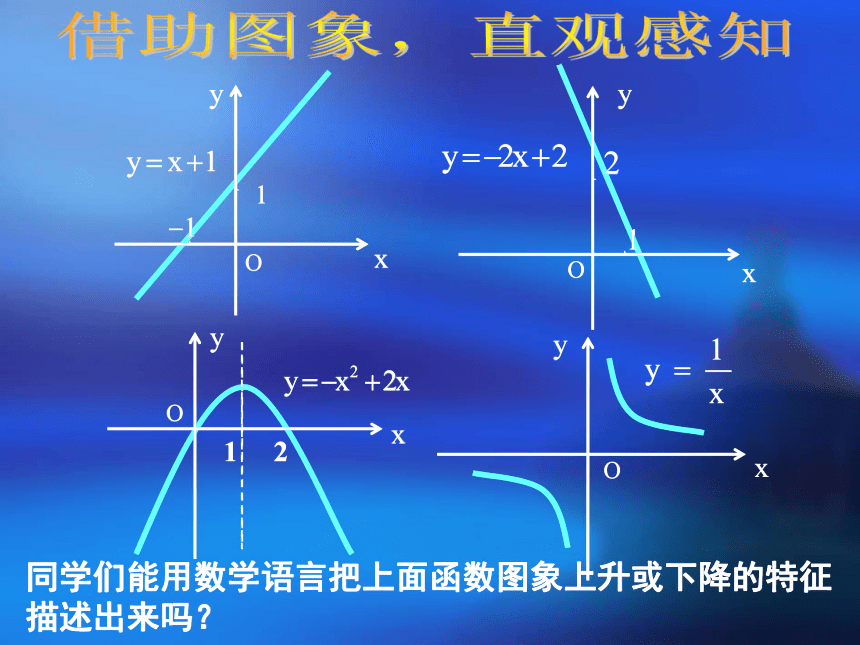
同学们能用数学语言把上面函数图象上升或下降的特征描述出来吗?
x
y
y = x
O
1
1
·
·
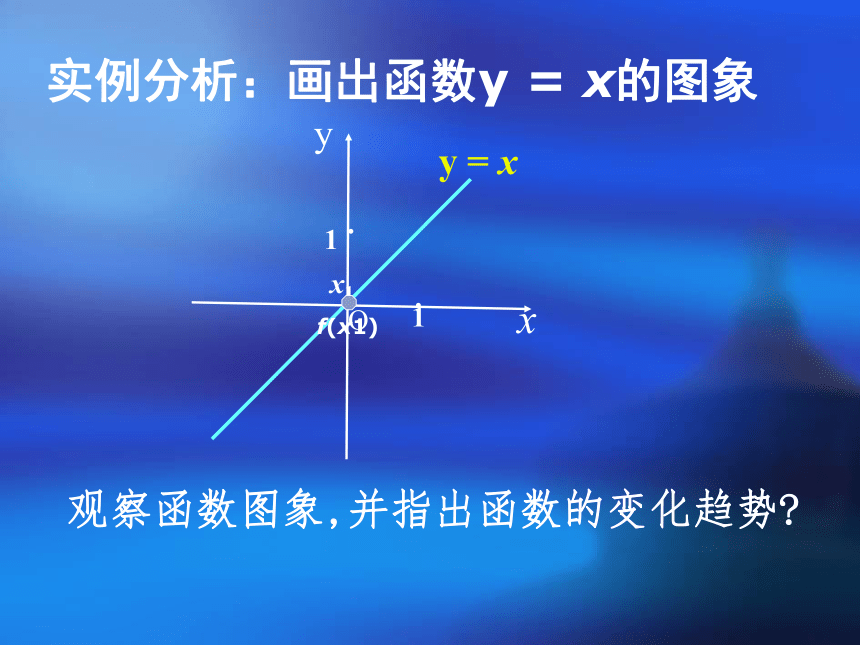
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
x
y
y = x
O
1
1
·
·
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
f(x1)
x1
x
y
y = x
O
1
1
·
·
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
x1
f(x1)
x
y
y = x
O
1
1
·
·
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
x1
f(x1)
x
y
y = x
O
1
1
·
·
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
x1
f(x1)
x
y
y = x
O
1
1
·
·
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
x1
f(x1)
O
x
y
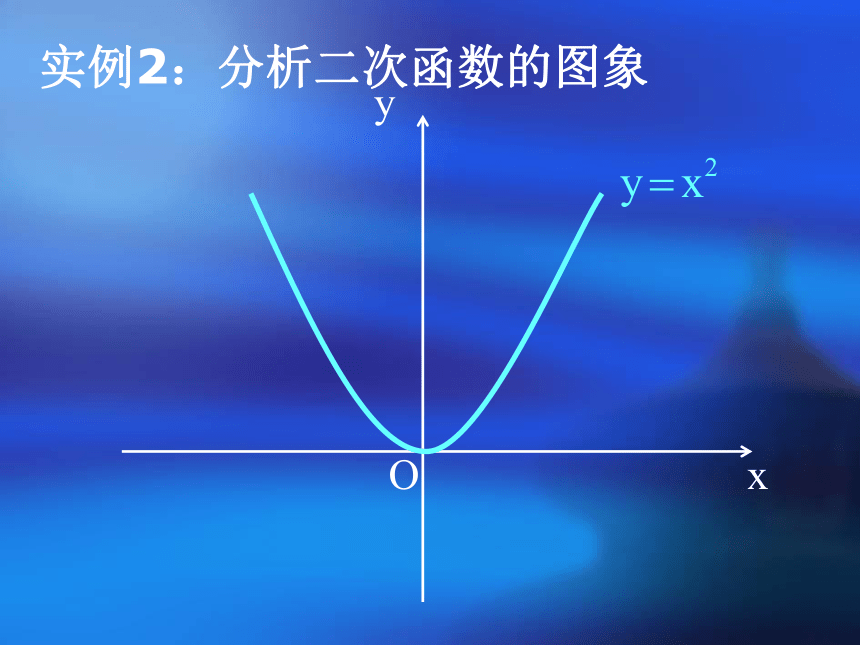
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
那么就说 函数f (x)在区间D上为增函数。
O
x
y
如何用x与 f(x)来描述上升的图象?
如何用x与 f(x)来描述下降的图象?
O
x
y
函数单调性的定义
那么就说 函数f (x)在区间D上为减函数。
0
y
x1
x2
f(x2)
f(x1)
0
y
x1
x2
f(x2)
f(x1)
x
x
·
·
·
·
在区间I内 在区间I内
图象 y=f(x) y=f(x)
图象特征 从左至右,图象上升 从左至右,图象下降
数量 特征 y随x的增大而增大
当x1<x2时, f(x1) < f(x2) y随x的增大而减小
当x1<x2时, f(x1) > f(x2)
(2)函数单调性是针对某个区间而言的,是一个局部性质;
(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
判断1:函数 f (x)= x2 是单调增函数;
x
y
o
(2)函数单调性是针对某个区间而言的,是一个局部性质;
(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
y
x
O
1
2
f(1)
f(2)
判断2:定义在R上的函数 f (x)满足 f (2)> f(1),则函数 f (x)在R上是增函数;
(3) x 1, x 2 取值具有任意性
⑷,对于某个具体函数的单调区间,可以是整个定义域(如一次函数),可以是定义域内某个区间(如二次函数),也可以根本不单调(如常函数).
⑸,函数在定义域内的两个区间A,B上都是
增(或减)函数,一般不能认为函数在
A∪B上是增(或减)函数
增区间
减区间
[-2,1]
[3,5]
[-5,-2]
[1,3]
说出函数f(x)=1/x 的单调区间,并指明在该区间的单调性
y
x
o
解:
(-∞,0)和 (0,+∞)都是函数f(x)的单调区间,在各个区间上都是递减的
注意:
不能说成(-∞,0) (0,+∞)
是减函数
说明:要了解函数在某一区间上是否具有单调性,可以通过图象法直接从图上进行观察,它是一种常用而又粗略的方法,但当函数的图象很难画出来时这种方法是不行的。这个时候,我们可以根据定义去证明函数的单调性。
问题1:你能判断函数
的单调性吗?
利用定义判定(证明)函数的增减性
a、任取定义域内某区间上的两变 量x1,x2,设x1b、判断f(x1) – f(x2)的正、负情况;
c、得出结论
我们回顾定义
问题2:如何从定义的角度证明函数f(x)=3x+2在R上是增函数?
f(x1)-f(x2)=(3 x1 +2)-(3 x2+2)
由x1即 f(x1)证明:设x1,x2是R上的任意两个实数,且x1=3( x1- x2)
于是 f(x1)-f(x2)<0
所以,函数f(x)=3x+2在R上是增函数。
取值
定号
变形
作差
判断
证明函数单调性的步骤
第一步:取值.即任取区间内的两个值,且x1第二步:作差变形.将f(x1)-f(x2)通过因式分解、配方、有理化等方法,向有利于判断差的符号的方向变形。
第三步:定号.确定差的符号,适当的时候需要进行讨论。
第四步:判断.根据定义作出结论。
取值
作差
变形
定号
判断
归纳:
解:二次函数 的对称轴为 ,
由图象可知只要 ,即 即可.
o
x
y
1
x
y
1
o
若二次函数 在区间 上单调递增,求a的取值范围。
(3)单调性的理论证明
(1)函数单调性的概念;
(2)判断函数单调区间的常用方法
方法二:通过定义去判断。
方法一:分析函数的图象。
2 若函数f(x)=ax2-(3a-1)x+a2在[1,+∞)上是增函数,求实数a的取值范围.
练习
1 下列函数,在区间(0,2)上是增函数的是( )
A.y= B.y=2x-1
C.y=1-2x D.y=(2x-1)2
深圳市年生产总值统计表
年份
生产总值
(亿元)
图示是某市一天24小时内的气温变化图。气温θ是关于时间 t 的函数,记为θ= f (t) ,观察这个气温变化图,说说气温在哪些时间段内是逐渐上升或下降的?
O
x
y
O
x
y
O
x
y
2
1
y
O
x
同学们能用数学语言把上面函数图象上升或下降的特征描述出来吗?
x
y
y = x
O
1
1
·
·
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
x
y
y = x
O
1
1
·
·
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
f(x1)
x1
x
y
y = x
O
1
1
·
·
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
x1
f(x1)
x
y
y = x
O
1
1
·
·
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
x1
f(x1)
x
y
y = x
O
1
1
·
·
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
x1
f(x1)
x
y
y = x
O
1
1
·
·
实例分析:画出函数y = x的图象
观察函数图象,并指出函数的变化趋势
x1
f(x1)
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
O
x
y
实例2:分析二次函数的图象
那么就说 函数f (x)在区间D上为增函数。
O
x
y
如何用x与 f(x)来描述上升的图象?
如何用x与 f(x)来描述下降的图象?
O
x
y
函数单调性的定义
那么就说 函数f (x)在区间D上为减函数。
0
y
x1
x2
f(x2)
f(x1)
0
y
x1
x2
f(x2)
f(x1)
x
x
·
·
·
·
在区间I内 在区间I内
图象 y=f(x) y=f(x)
图象特征 从左至右,图象上升 从左至右,图象下降
数量 特征 y随x的增大而增大
当x1<x2时, f(x1) < f(x2) y随x的增大而减小
当x1<x2时, f(x1) > f(x2)
(2)函数单调性是针对某个区间而言的,是一个局部性质;
(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
判断1:函数 f (x)= x2 是单调增函数;
x
y
o
(2)函数单调性是针对某个区间而言的,是一个局部性质;
(1)如果函数 y =f(x)在区间I是单调增函数或单调减函数,那么就说函数 y =f(x)在区间I上具有单调性。
y
x
O
1
2
f(1)
f(2)
判断2:定义在R上的函数 f (x)满足 f (2)> f(1),则函数 f (x)在R上是增函数;
(3) x 1, x 2 取值具有任意性
⑷,对于某个具体函数的单调区间,可以是整个定义域(如一次函数),可以是定义域内某个区间(如二次函数),也可以根本不单调(如常函数).
⑸,函数在定义域内的两个区间A,B上都是
增(或减)函数,一般不能认为函数在
A∪B上是增(或减)函数
增区间
减区间
[-2,1]
[3,5]
[-5,-2]
[1,3]
说出函数f(x)=1/x 的单调区间,并指明在该区间的单调性
y
x
o
解:
(-∞,0)和 (0,+∞)都是函数f(x)的单调区间,在各个区间上都是递减的
注意:
不能说成(-∞,0) (0,+∞)
是减函数
说明:要了解函数在某一区间上是否具有单调性,可以通过图象法直接从图上进行观察,它是一种常用而又粗略的方法,但当函数的图象很难画出来时这种方法是不行的。这个时候,我们可以根据定义去证明函数的单调性。
问题1:你能判断函数
的单调性吗?
利用定义判定(证明)函数的增减性
a、任取定义域内某区间上的两变 量x1,x2,设x1
c、得出结论
我们回顾定义
问题2:如何从定义的角度证明函数f(x)=3x+2在R上是增函数?
f(x1)-f(x2)=(3 x1 +2)-(3 x2+2)
由x1
于是 f(x1)-f(x2)<0
所以,函数f(x)=3x+2在R上是增函数。
取值
定号
变形
作差
判断
证明函数单调性的步骤
第一步:取值.即任取区间内的两个值,且x1
第三步:定号.确定差的符号,适当的时候需要进行讨论。
第四步:判断.根据定义作出结论。
取值
作差
变形
定号
判断
归纳:
解:二次函数 的对称轴为 ,
由图象可知只要 ,即 即可.
o
x
y
1
x
y
1
o
若二次函数 在区间 上单调递增,求a的取值范围。
(3)单调性的理论证明
(1)函数单调性的概念;
(2)判断函数单调区间的常用方法
方法二:通过定义去判断。
方法一:分析函数的图象。
2 若函数f(x)=ax2-(3a-1)x+a2在[1,+∞)上是增函数,求实数a的取值范围.
练习
1 下列函数,在区间(0,2)上是增函数的是( )
A.y= B.y=2x-1
C.y=1-2x D.y=(2x-1)2
