高一数学《1.3.1单调性与最大小值 》课件(人教版必修一)
文档属性
| 名称 | 高一数学《1.3.1单调性与最大小值 》课件(人教版必修一) |  | |
| 格式 | zip | ||
| 文件大小 | 156.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-18 08:27:41 | ||
图片预览





文档简介
(共17张PPT)
【教学重点】
【教学目标】
【教学难点】
利用函数的单调性求最值.
理解函数最大(小)值及其几何意义
会利用函数的单调性及图象求函数的最值
逐步渗透数形结合的数学思想方法
难点:函数在给定区间上的最大(小)值
教法:自学辅导法、讨论法、讲授法
学法:归纳—讨论—练习
【教学方法】
【教学手段】
多媒体电脑与投影仪
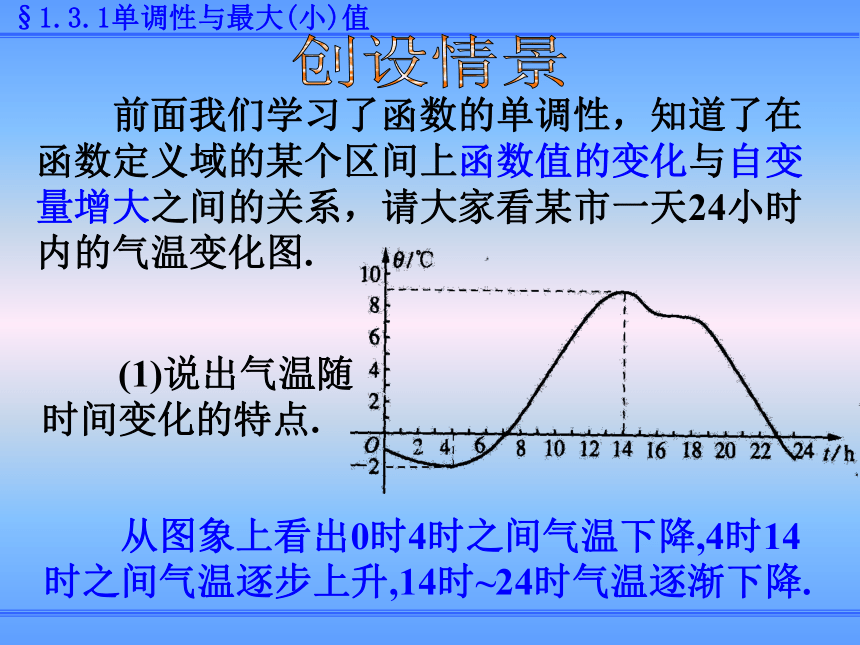
前面我们学习了函数的单调性,知道了在函数定义域的某个区间上函数值的变化与自变量增大之间的关系,请大家看某市一天24小时内的气温变化图.
(1)说出气温随时间变化的特点.
从图象上看出0时4时之间气温下降,4时14时之间气温逐步上升,14时~24时气温逐渐下降.
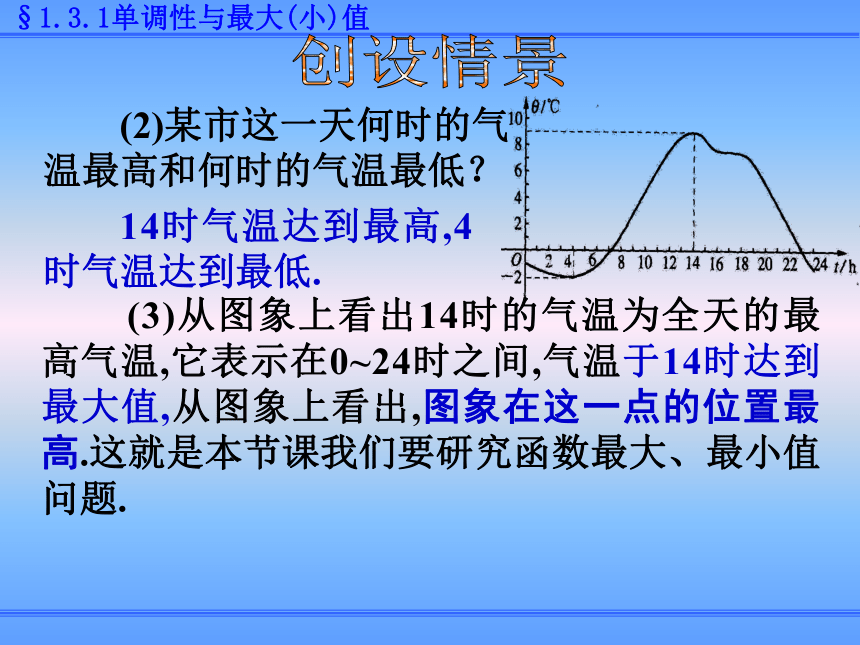
(2)某市这一天何时的气温最高和何时的气温最低?
14时气温达到最高,4时气温达到最低.
(3)从图象上看出14时的气温为全天的最高气温,它表示在0~24时之间,气温于14时达到最大值,从图象上看出,图象在这一点的位置最高.这就是本节课我们要研究函数最大、最小值问题.
设函数f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x I,都有f(x)≤M;
(2)存在x0 I,使得f(x0)=M.
则称M是函数的最大值(maximum value)
1.函数的最大值:
上面我们从直观的感受知道了最值的概念,下面给出严格的定义.
2.函数最大值应该是所有函数值中最大的,即对于任意的x∈I,都有f(x)≤M.
注意:1.函数最大值首先应该是某一个函数值,即存在x0∈I,使得f(x0) = M;
定义中的两个条件缺一不可,只有(1)没有(2)不存在最大值点,而只有(2)没有(1),M不一定是函数y=f(x)的最大值.比照最大值的定义, 最小值是如何定义的
(1)对于任意的x I,都有f(x)≥M;
(2)存在x0 I,使得f(x0)=M.
则称M是函数的最小值(minimum value)
设函数f(x)的定义域为I,如果存在实数M满足:
2.函数的最小值:
函数的最大值从图象上看是在指定的区间里最高位置对应的点的纵坐标,好象有一种一览众山小的情景.同样函数的最小值从图象上看是在指定的区间里最低位置对应的点的纵坐标,好像有一种坐井观天的情景.
请大家思考, 是否每个函数都有最大值,最小值?举例说明.
一个 函数不一定有最值.
有的函数可能只有一个最大(或小)值.
如果一个函数存在最值,那么函数的最值都是唯一的,但取最值时的自变量可以有多个.
【1】求函数y=x2-2x-1的值域和最值.
(1) x∈[0, 3]
(2) x∈(2, 4]
(3) x∈[-2, -1]
ymin=f(1)=-2,
ymax=f(3)=2.
值域[-2,2]
ymax=f(4)=7.
值域(-1,7]
ymax=f(-2)=7.
值域[2,7]
ymin=f(-1)=2,
例2.求函数 在区间[2,6]上的最大值和最小值.
解:设x1, x2是区间[2,6]上的任意两个实数,且x1由20,(x1-1)(x2-1)>0,
于是
因此,函数 在区间[2,6]上的两个端点上分别取得最大值和最小值.
所以,函数 是区间[2,6]上的减函数.
当x=2时取最大值
当x=6时取最小值
即
x
y
o
1
2
3
4
5
6
1
3
2
【2】已知函数 求函数的最大值和最小值.
【3】在已知函数f(x)=4x2-mx+1,在(-∞,-2]上递减,在[-2,+∞)上递增,则f(x)在[1,2]上的值域__________.
[21,49]
分析:设
则
确定 正负号的关键,是确定
的正负号.
由于x1, x2在同一区间内,
要使 则需
要使 则需
【4】求函数 的最大值.
【4】求函数 的最大值.
解:任取x1, x2 , x1, x2∈[2,4],且x1< x2,
当 时,
所以函数f(x)在[2,4]上是减函数.
同理函数f(x)在[4,10]上是增函数.
解:∵函数
在[2,4]上是减函数.
所以f(x)在[2,4]上有最大值,
∵函数
在[4,10]上是增函数.
所以f(x)在[4,10]上有最大值,
所以函数f(x)在[2,10]上的最大值是
1.函数的最大(小)值的定义及几何意义.
2.三类函数的最值的求法.
利用二次函数的性质(配方法)求函数的最大(小)值.
利用图象求函数的最大(小)值.
利用函数单调性求函数的最大(小)值
如果函数y=f(x)在区间[a,b]上单调递增,则函数y=f(x)在x=a处有最小值f(a),在x=b处有最大值f(b).
函数在其定义域上的最大值,其几何意义是图象上最高点的纵坐标;最小值为图象上最低点的纵坐标.
【教学重点】
【教学目标】
【教学难点】
利用函数的单调性求最值.
理解函数最大(小)值及其几何意义
会利用函数的单调性及图象求函数的最值
逐步渗透数形结合的数学思想方法
难点:函数在给定区间上的最大(小)值
教法:自学辅导法、讨论法、讲授法
学法:归纳—讨论—练习
【教学方法】
【教学手段】
多媒体电脑与投影仪
前面我们学习了函数的单调性,知道了在函数定义域的某个区间上函数值的变化与自变量增大之间的关系,请大家看某市一天24小时内的气温变化图.
(1)说出气温随时间变化的特点.
从图象上看出0时4时之间气温下降,4时14时之间气温逐步上升,14时~24时气温逐渐下降.
(2)某市这一天何时的气温最高和何时的气温最低?
14时气温达到最高,4时气温达到最低.
(3)从图象上看出14时的气温为全天的最高气温,它表示在0~24时之间,气温于14时达到最大值,从图象上看出,图象在这一点的位置最高.这就是本节课我们要研究函数最大、最小值问题.
设函数f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x I,都有f(x)≤M;
(2)存在x0 I,使得f(x0)=M.
则称M是函数的最大值(maximum value)
1.函数的最大值:
上面我们从直观的感受知道了最值的概念,下面给出严格的定义.
2.函数最大值应该是所有函数值中最大的,即对于任意的x∈I,都有f(x)≤M.
注意:1.函数最大值首先应该是某一个函数值,即存在x0∈I,使得f(x0) = M;
定义中的两个条件缺一不可,只有(1)没有(2)不存在最大值点,而只有(2)没有(1),M不一定是函数y=f(x)的最大值.比照最大值的定义, 最小值是如何定义的
(1)对于任意的x I,都有f(x)≥M;
(2)存在x0 I,使得f(x0)=M.
则称M是函数的最小值(minimum value)
设函数f(x)的定义域为I,如果存在实数M满足:
2.函数的最小值:
函数的最大值从图象上看是在指定的区间里最高位置对应的点的纵坐标,好象有一种一览众山小的情景.同样函数的最小值从图象上看是在指定的区间里最低位置对应的点的纵坐标,好像有一种坐井观天的情景.
请大家思考, 是否每个函数都有最大值,最小值?举例说明.
一个 函数不一定有最值.
有的函数可能只有一个最大(或小)值.
如果一个函数存在最值,那么函数的最值都是唯一的,但取最值时的自变量可以有多个.
【1】求函数y=x2-2x-1的值域和最值.
(1) x∈[0, 3]
(2) x∈(2, 4]
(3) x∈[-2, -1]
ymin=f(1)=-2,
ymax=f(3)=2.
值域[-2,2]
ymax=f(4)=7.
值域(-1,7]
ymax=f(-2)=7.
值域[2,7]
ymin=f(-1)=2,
例2.求函数 在区间[2,6]上的最大值和最小值.
解:设x1, x2是区间[2,6]上的任意两个实数,且x1
于是
因此,函数 在区间[2,6]上的两个端点上分别取得最大值和最小值.
所以,函数 是区间[2,6]上的减函数.
当x=2时取最大值
当x=6时取最小值
即
x
y
o
1
2
3
4
5
6
1
3
2
【2】已知函数 求函数的最大值和最小值.
【3】在已知函数f(x)=4x2-mx+1,在(-∞,-2]上递减,在[-2,+∞)上递增,则f(x)在[1,2]上的值域__________.
[21,49]
分析:设
则
确定 正负号的关键,是确定
的正负号.
由于x1, x2在同一区间内,
要使 则需
要使 则需
【4】求函数 的最大值.
【4】求函数 的最大值.
解:任取x1, x2 , x1, x2∈[2,4],且x1< x2,
当 时,
所以函数f(x)在[2,4]上是减函数.
同理函数f(x)在[4,10]上是增函数.
解:∵函数
在[2,4]上是减函数.
所以f(x)在[2,4]上有最大值,
∵函数
在[4,10]上是增函数.
所以f(x)在[4,10]上有最大值,
所以函数f(x)在[2,10]上的最大值是
1.函数的最大(小)值的定义及几何意义.
2.三类函数的最值的求法.
利用二次函数的性质(配方法)求函数的最大(小)值.
利用图象求函数的最大(小)值.
利用函数单调性求函数的最大(小)值
如果函数y=f(x)在区间[a,b]上单调递增,则函数y=f(x)在x=a处有最小值f(a),在x=b处有最大值f(b).
函数在其定义域上的最大值,其几何意义是图象上最高点的纵坐标;最小值为图象上最低点的纵坐标.
