高一数学《 1.1.3 集合的基本运算(第二课时)》课件(人教版必修一)
文档属性
| 名称 | 高一数学《 1.1.3 集合的基本运算(第二课时)》课件(人教版必修一) |  | |
| 格式 | zip | ||
| 文件大小 | 19.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-18 08:28:59 | ||
图片预览





文档简介
(共15张PPT)
一 学习目标
在理解两个集合的并集与交集的含义的基础上理解全集和补集的概念.
能使用Venn图表达集合的关系和运算体会直观图示对理解抽象概念的作用.
能够正确的理解不同语言表示的集合的本质并且能够在解题时准确表达.
U
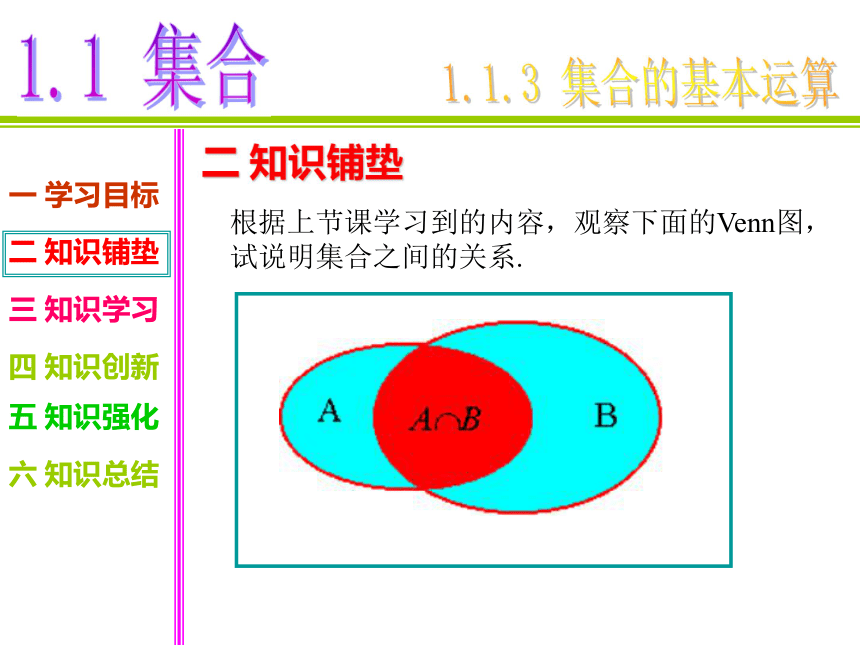
二 知识铺垫
根据上节课学习到的内容,观察下面的Venn图,试说明集合之间的关系.
三 知识学习
1.全集
一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集(universe set),通常记作U.
注意:全集是相对于所研究问题而言的一个相对概念,它含有与所研究问题有关的各个集合的全部元素.因此全集因问题而异.例如在研究数集时,常常把实数集看作全集.
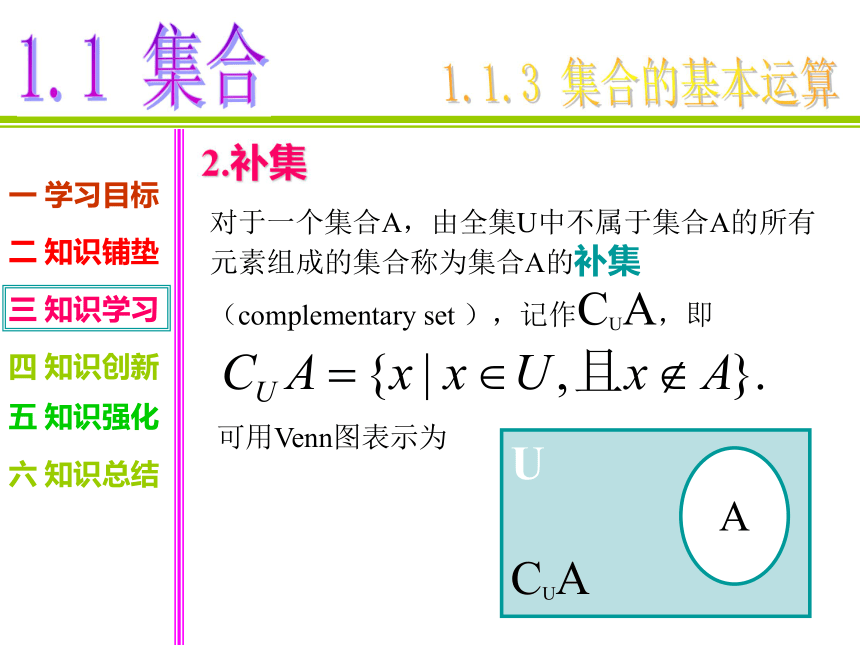
2.补集
对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A的补集(complementary set ),记作CUA,即
可用Venn图表示为
U
CUA
A
例8 设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},求CuA,CuB.
解:根据题意可知,U={1,2,3,4,5,6,7,8},
所以 CuA={4,5,6,7,8}
CuB={1,2,7,8} .
例9 设全集U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形}
求A∩B,Cu(A∪B).
练习:1.判断正误
(1)若U={四边形},A={梯形},
则CUA={平行四边形}
(2)若U是全集,且A B,
则 CUA CUB
(3)若U={1,2,3},A=U,
则CUA=
设集合A={|2a-1|,2},
B={2,3,a2+2a-3}且CBA={5},
求实数a的值。
3. 已知全集U={1,2,3,4,5},
非空集A={x U|x2-5x+q=0},
求CUA及q的值。
四 知识创新
1.表示全集和补集的三种数学语言互译.
U
CUA
A
文字语言
符号语言
图形语言
2.集合的基本运算:交、并、补的两条运算性质
U
五 知识强化
练习1 已知全集U={1,2,3,4,5,6,7}, A={2,4,5},B={1,3,5,7}求 A∩(CUB), (CUA)∩ (CUB).
解:由题意可知
CUA={1,3,6,7}, CUB={2,4,6},
则A∩(CUB)={2,4},
(CUA)∩ (CUB)={6}.
练习2 设集合A={x|(x-3)(x-a)=0,a∈R},B={x|(x-4)(x- 1)=0},求A∪B,A∩B.
解:由题意可知
B={1,4}, A={a,3}
若a=1,则A∪B={1,3,4} ,A∩B={1},
若a=4,则A∪B={1,3,4} ,A∩B={4},
若a=3,则A∪B={1,3,4} ,A∩B= ,
若a≠1,且a≠4,a≠3,则
A∪B={1,3,4,a}, A∩B= ,
六 知识总结
本节我们在集合的并、交两种基本运算的基础上学习了全集和补集的概念,在掌握概念的基础上能够熟练运用自然语言、符号语言、图形语言来表示和理解集合的全集和补集以及并集、交集的综合运算.
作业:课本第12页A10,B4
一 学习目标
在理解两个集合的并集与交集的含义的基础上理解全集和补集的概念.
能使用Venn图表达集合的关系和运算体会直观图示对理解抽象概念的作用.
能够正确的理解不同语言表示的集合的本质并且能够在解题时准确表达.
U
二 知识铺垫
根据上节课学习到的内容,观察下面的Venn图,试说明集合之间的关系.
三 知识学习
1.全集
一般地,如果一个集合含有我们所研究问题中所涉及的所有元素,那么就称这个集合为全集(universe set),通常记作U.
注意:全集是相对于所研究问题而言的一个相对概念,它含有与所研究问题有关的各个集合的全部元素.因此全集因问题而异.例如在研究数集时,常常把实数集看作全集.
2.补集
对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A的补集(complementary set ),记作CUA,即
可用Venn图表示为
U
CUA
A
例8 设U={x|x是小于9的正整数},A={1,2,3},B={3,4,5,6},求CuA,CuB.
解:根据题意可知,U={1,2,3,4,5,6,7,8},
所以 CuA={4,5,6,7,8}
CuB={1,2,7,8} .
例9 设全集U={x|x是三角形},A={x|x是锐角三角形},B={x|x是钝角三角形}
求A∩B,Cu(A∪B).
练习:1.判断正误
(1)若U={四边形},A={梯形},
则CUA={平行四边形}
(2)若U是全集,且A B,
则 CUA CUB
(3)若U={1,2,3},A=U,
则CUA=
设集合A={|2a-1|,2},
B={2,3,a2+2a-3}且CBA={5},
求实数a的值。
3. 已知全集U={1,2,3,4,5},
非空集A={x U|x2-5x+q=0},
求CUA及q的值。
四 知识创新
1.表示全集和补集的三种数学语言互译.
U
CUA
A
文字语言
符号语言
图形语言
2.集合的基本运算:交、并、补的两条运算性质
U
五 知识强化
练习1 已知全集U={1,2,3,4,5,6,7}, A={2,4,5},B={1,3,5,7}求 A∩(CUB), (CUA)∩ (CUB).
解:由题意可知
CUA={1,3,6,7}, CUB={2,4,6},
则A∩(CUB)={2,4},
(CUA)∩ (CUB)={6}.
练习2 设集合A={x|(x-3)(x-a)=0,a∈R},B={x|(x-4)(x- 1)=0},求A∪B,A∩B.
解:由题意可知
B={1,4}, A={a,3}
若a=1,则A∪B={1,3,4} ,A∩B={1},
若a=4,则A∪B={1,3,4} ,A∩B={4},
若a=3,则A∪B={1,3,4} ,A∩B= ,
若a≠1,且a≠4,a≠3,则
A∪B={1,3,4,a}, A∩B= ,
六 知识总结
本节我们在集合的并、交两种基本运算的基础上学习了全集和补集的概念,在掌握概念的基础上能够熟练运用自然语言、符号语言、图形语言来表示和理解集合的全集和补集以及并集、交集的综合运算.
作业:课本第12页A10,B4
